重抽样方差成分检验的多位点关联分析*

唐明生黄水平金英良张耀东赵 杨陈 峰曾 平△

重抽样方差成分检验的多位点关联分析*

唐明生1黄水平1金英良1张耀东1赵 杨2陈 峰2曾 平1△

目的在线性混合模型框架下探索基于重抽样方差成分的似然比检验多位点关联分析方法。方法假设SNP位点效应服从正态分布，将多位点关联分析转化为对随机效应方差的似然比检验，采用重抽样方法获得统计量的零分布，通过混合分布提高计算速度。结果模拟研究显示重抽样检验以及混合分布表现良好，能够有效控制I型错误，统计效能优于现有方法。结论似然比检验是一种高效能的多位点关联检验方法，通过对置换和bootstrap分布的有效近似，基于重抽样的似然比方差成分检验，在保持良好统计效能的同时，能明显降低计算负荷。

关联研究 方差成分 线性混合模型 似然比检验 置换法 非参数bootstrap法

在全基因组关联性研究（genome w ide association study，GWAS）中，相对于单位点分析，多位点分析已经成为一种有效的关联性检验方法［1－8］。单位点分析对成千上万个单核苷酸多态性（single nucleotide polymorphisms，SNP）依次检验，要求十分严格的多重检验水准［9］。相反，多位点分析同时检验一组SNP是否与表型相关，有诸多优点：能显著降低多重比较负担，能利用SNP间连锁不平衡信息来提高效能。考虑到位点间联合效应，SNP集合常根据基因选定，也即位于相同基因内的变异位点组成一个集合［10］。

多位点分析可采用固定效应模型和固定效应检验执行，如Wald检验；但固定效应检验在SNP位点个数较多时效能低下。另一方面，在线性混合模型下假设SNP具有随机效应，能够将多位点分析转化为对随机效应的方差成分检验；现阶段主要通过得分检验来实现这一目的［1，8，11－16］。得分检验只需拟合零模型，计算效率高；但结果相对保守，特别是在小样本的情况下［16］。本文尝试采用似然比检验（likelihood ratio test，LRT）及限制性似然比检验（restricted likelihood ratio test，ReLRT）对SNP集合进行关联性检验［17－19］，通过置换及bootstrap［20－23］等重抽样方法获得统计量的零分布。事实上，在关联性研究中为了避免导出解析解，重抽样技术已经广泛应用于复杂假设检验［6，24－29］。然而，重抽样属于计算密集型统计方法，为了减少计算负荷，本文进一步通过混合分布来近似重抽样分布，以提高似然比检验的计算速度。最后通过模拟和实际数据来展示本文的方法。

资料与方法

1．线性混合模型和似然的推断

用线性混合模型［30－32］来描述多个SNP位点和表型之间的关系：

Y是n维连续性表型，X为n×m的协变量矩阵（m为协变量个数），具有固定效应α，G表示n×p的SNP基因型矩阵（编码0，1，2，p为SNP个数），具有随机效应b，服从均数为0、方差为τ的正态分布。ε为残差项，服从均数为0、方差为σ2的正态分布。

检验G与表型Y之间的关系等价于检验随机效应H0：b＝0，也等价于检验方差成分H0：τ＝0。这样，通过混合效应模型SNP集合的关联分析就转化为对随机效应方差成分的假设检验。

省略常数项，模型（1）的对数似然函数和限制性对数似然函数分别为：

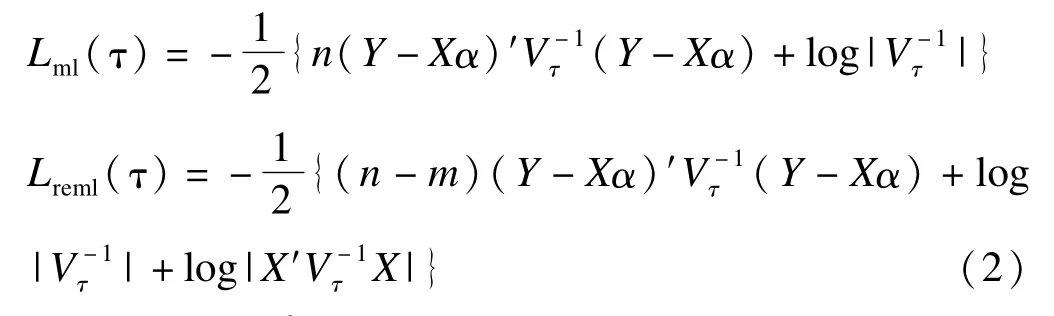
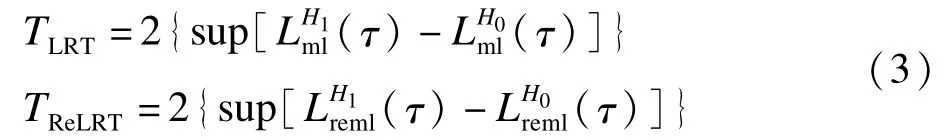
与得分检验不同，似然比检验和限制性似然比要求同时拟合零模型和备择模型，本文通过R软件的lm和lme软件包［33－34］来估计线性模型和混合效应模型。

在H0的条件下，τ位于参数空间的边缘；由于这种限制，TLRT和TReLRT的零分布不再渐近服从标准的卡方分布［35］，先前的研究显示在一定条件下，TLRT和TReLRT渐近服从的混合分布［18］。但是，该混合分布的假定条件在实际中很难得到满足。Pinheiro和Bates提出了0．65：0．35的混合分布［36］。本文模拟研究表明，在多位点似然比关联性分析中两种混合比例都不正确。事实上，混合分布比例参数依具体情况而定，依赖于特殊矩阵的特征值［37－39］。本文通过重抽样方法来获得似然比统计量和限制性似然比统计量的零分布。

2．重抽样算法

当烘丝机入料电子秤不再检测到烟丝，烘丝机即由生产状态切换至收尾状态，筒壁Ⅰ区、Ⅱ区温度控制器停止工作，Ⅰ区、Ⅱ区蒸汽压力控制阀保持其最后适用的修正变量60 s后；Ⅰ区、Ⅱ区蒸汽压力控制阀开始逐渐关闭Ⅰ区、Ⅱ区蒸汽阀门开度，在20 s内完全关闭Ⅰ区、Ⅱ区，蒸汽停止加热筒壁。在此过程中，因为烘丝机蒸汽压力控制阀对筒壁Ⅰ区、Ⅱ区蒸汽压力保持以及对Ⅰ区、Ⅱ区蒸汽的关闭均为同时进行，且烘丝机由收尾状态至蒸汽压力保持的延时时间以及对筒壁Ⅰ区和Ⅱ区蒸汽压力的保持时间较长，使烘丝机热惯性过大，导致了收尾状态产生大量的干尾烟丝。

置换和bootstrap法都是通过重复抽样获得零分布，不同之处在于两者的抽样方式。置换法通过扰乱原始数据的标签产生，需要将Y和X视为一个整体，即置换是对Y和X同时进行，而保持G固定不变；这样可以保持Y与X的相关结构。这里潜在假设G和X是独立的。bootstrap法采用非参数有放回抽样产生，即是从中有放回抽得的样本。以上两种产生数据D*的方法是等价的［21－22］。在bootstrap算法中，最自然的抽样是从原始残差X中进行抽样；然而Davison和Hinkley［21］指出，当是异方差性时，从修正残差中 抽样更好，h为杠杆值。置换和bootstrap检验的P值采用蒙特卡洛方法获得，即通过有限次数（设为S）的重抽样方式代替。很多研究表明，在检验水准较大时（如0．05），S＝1000或2000时P值就趋于相对稳定［20－22］。

3．近似分布

假设TLRT和TReLRT服从混合分布

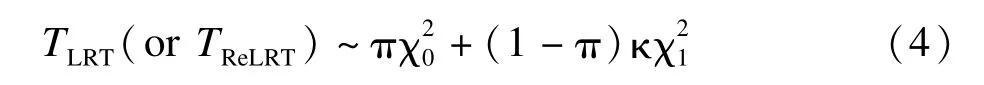
κ是未知的尺度参数分别为自由度为0和1的卡方分布。假设近似零分布为卡方混合的原因在于：（I）在适当的条件下，TLRT和TReLRT取0的概率不为零，因此包括作为退化到0的分布；（II）在标准条件下，即参数在其参数空间的内部时，TLRT和TReLRT渐近服从自由度为1的卡方分布［40］，因此包括表示可能的偏离；类似的混合分布也被应用在其他地方［17，36］。κ的估计值为：

本文采用局部概率法来估计π［38－39］：

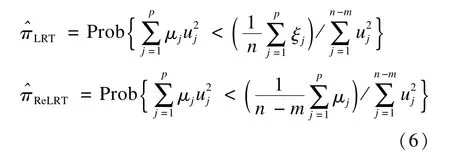
μ是G′P0G的特征值，P0＝In－X（X′X）－1X′，ξ是G′G的特征值，u是独立标准正态分布的随机变量。局部概率法相对于矩估计法的优势在于：其π估计值与L的选择无关，因此π估计值是稳定的，并会导致更加精确的估计。对（6）式可采用Davies法［42］获得π的估计值然后将代入（5）中可算得式（6）还进一步表明：TLRT和TReLRT的零分布依具体情况而定，固定比例的卡方混合分布是不恰当的。

结 果

用FEV1下降率的数据［43］来展示本文提出的LRT和ReLRT多位点关联性分析方法，样本量为301，用FEV1下降的斜率ES作为表型［43］。结果表明，位点rs9469089与FEV1相关联；该位点位于染色体6p21．32，在基因RNF5的第一个内含子区域内，而RNF5编码膜结合型泛素连接酶。在该数据中RNF5一共包含14个SNP。

首先评价I类错误控制。假设表型来自于

X1和X2分别为标准正态变量和二分类变量，模拟次数为105次。重抽样中S＝2000，对于近似混合分布，取L＝2000、1500、1000、800、500、300和100。用m lp1－m lp7对应以上各L取值。在评价统计效能时，假设表型来自于

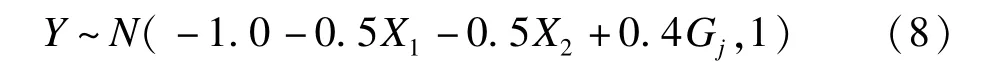
这里，j取1到14，即每个SNP位点依次被设为关联位点，效应值为0．20，0．30和0．40，重复103次，则一共运行1．4×104次。P值用小于检验水准α＝0．05的比例估计。

2．解释和说明

模拟结果显示，在LRT和ReLRT中κ与π的平均值分别为1．118和0．909与0．865和0．604；这些数值和本文特定的基因型矩阵和协变量矩阵相关，其他不同的选择会导致不同的κ和π估计值。这表明Self和Liang［17］及Pinheiro和Bates［36］提出的零分布是不合理的，同时也表明LRT和ReLRT服从不同的零分布。图1表明参数π在有限的范围内变化（这是因为在所有的模拟中使用相同的G和相似的X），将其固定取某一常数是不适当的。根据公式（6），π随数据集而变化，因此直接根据数据估计π更合理。此外，模拟还表明，相对于在ReLRT中，κ估计值在LRT中更大（图1）。κ估计值的精度随着L减小而降低；然而，不同L值通常产生非常相似的结果。

图2表明对LRT而言，模拟算法［39，45］估计的I类错误率结果偏于保守，而置换和bootstrap检验可以调整LRT的这种保守性；混合分布对I类错误的控制与L取值无关。ReLRT在所有情形下对I类错误控制都表现良好；这可能是因为LRT对方差成分的估计是有偏估计，而ReLRT对方差成分的估计是无偏估计［46－47］。LRT模拟算法的统计效能低于相应置换和bootstrap检验的统计效能；在ReLRT中，模拟算法、置换和bootstrap检验的统计效差异微小（图3）。此外，通常次要等位基因频率高，统计效能也较高（图3）。

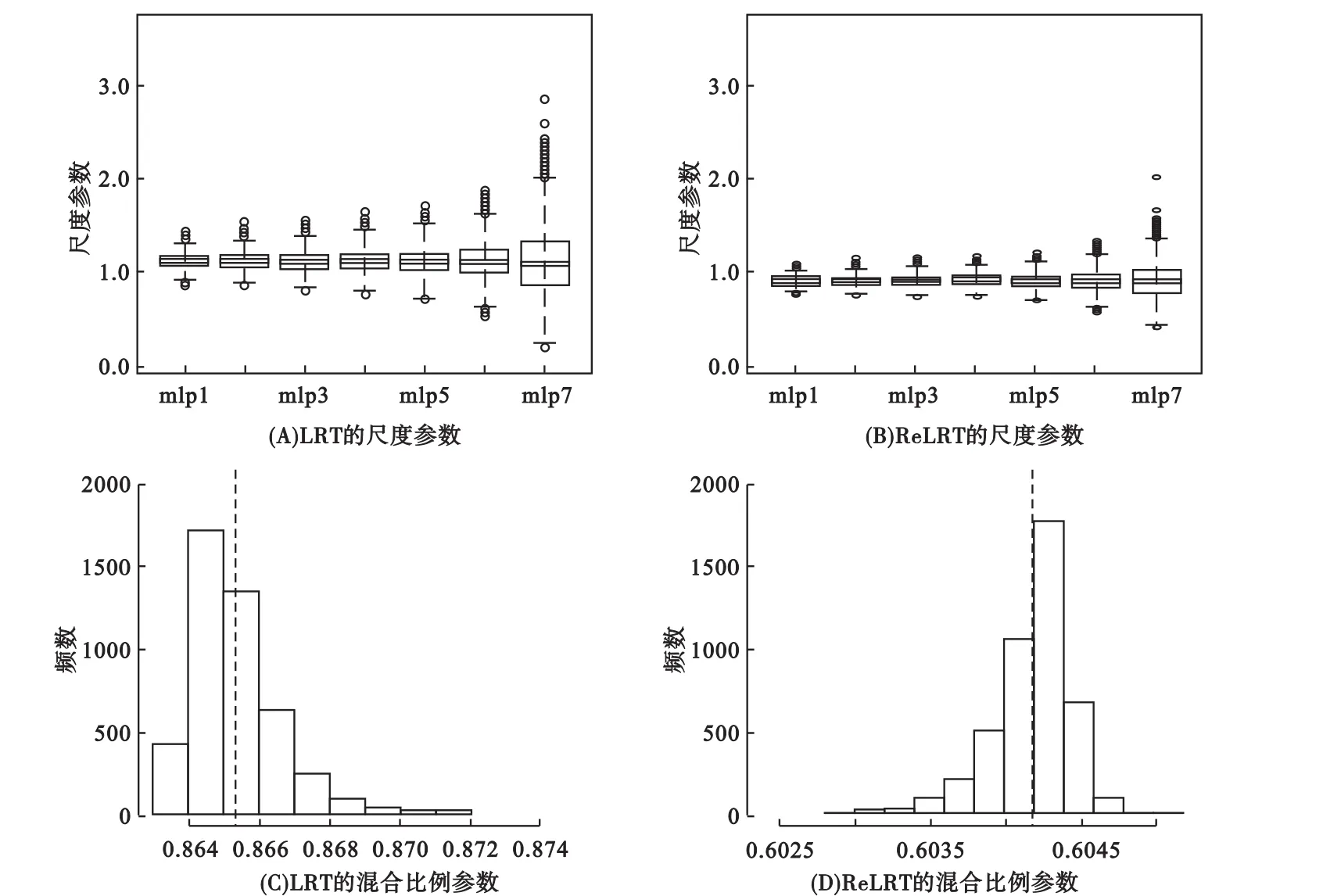
图1 在不同的L值下，LRT和ReLRT近似混合分布的尺度参数κ和混合比例参数π的估计值

图2 LRT和ReLRT I类错误率的置换或bootstrap算法估计

LRT和ReLRT的统计效能通常高于得分检验的统计效能。对于得分检验、LRT和ReLRT，在模拟效应为0．40时三者的平均统计效能分别为0．474、0．544和0．545；模拟效应为0．30时为0．315，0．453和0．510；模拟效应为0．20时为0．179，0．232和0．250。图3表明：对于LRT（或ReLRT），置换和bootstrap两种检验方法的统计效能相似。

在FEV1数据中将斜率（即ES）作为表型［43］，内毒素暴露和BMI作为协变量，采用LRT和ReLRT以及得分检验来分析基因RNF5的关联性（表1）。从表1可见，在LRT中由模拟算法获得的P值比其他情形下的P值大，置换和bootstrap检验的P值更小；ReLRT的P值变化较小。这些结果和模拟的结论一致。得分检验的P值为0．027。

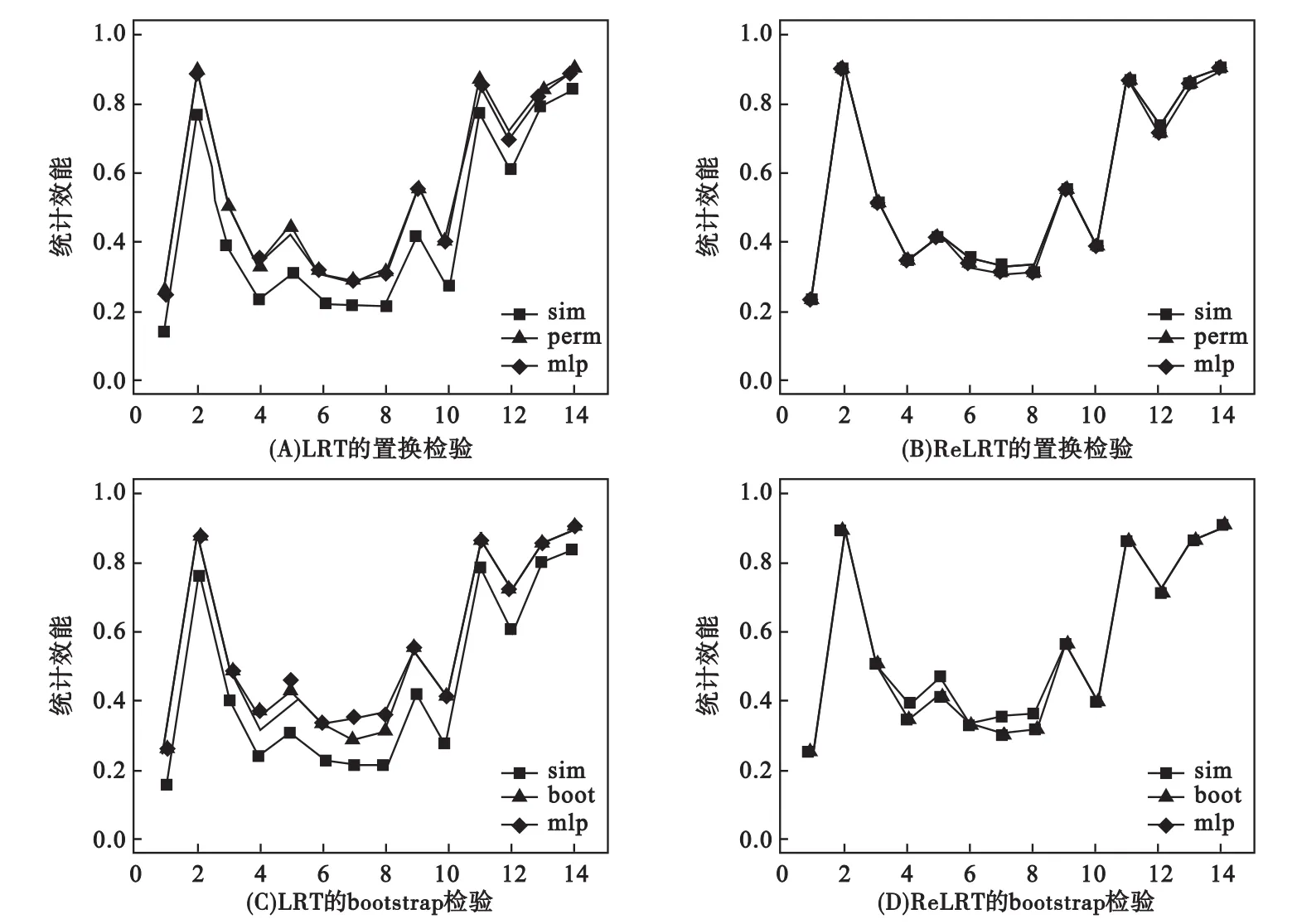
图3 LRT和ReLRT统计效能的置换或bootstrap算法估计

表1 FEV1数据中基因RNF5的P值

讨 论

本文在线性混合模型框架下研究了基于重抽样的似然比多位点关联分析，在该框架下，一组SNP位点与表型的关联性分析被转化为对随机效应的方差成分检验［1，11－16］。本文采用重抽样技术（置换和bootstrap）获得似然比统计量的零分布，避免了复杂的数学推导。此外，还通过混合分布近似置换或bootstrap分布。本文采用非参数而不是参数的bootstrap法，其原因在于非参数bootstrap法更加稳健［20－21］。模拟表明，对于限制似然比检验，置换和bootstrap法能有效控制I类错误且统计效能高于现有的得分检验方法；然而，对于似然比检验，其I类错误未能得到有效控制。研究还发现，对于小样本基于模拟算法的似然比检验［39，41］会导致保守的结果，而随着样本量的增加，似然比检验表现趋于正常［45］。

重抽样方法的主要缺点是耗时，本文利用混合分布近似来减少计算负荷。模拟表明，近似分布能显著减少计算时间。例如，L＝100时的混合分布比S＝2000时的重抽样检验计算时间大约减少20倍。更重要的是，在大规模多位点关联分析时，要求更加精确的P值，这需要成千上万次的置换或bootstrap抽样，导致重抽样方法不可行；而近似混合分布能够适合这种情形。如前所述，在混合分布的参数估计中，和其他方法相比，局部概率法具有数值稳定的优点。

类似的重抽样方法也被应用在其他情形，例如，Faraway［48］和Samuh等［49］提出了线性混合模型似然比检验的参数bootstrap法，Fitzmaurice等［50］，Lee和Braun［51］，Samuh［49］提出了似然比检验置换法，Sinha［52］在广义线性混合模型下通过参数bootstrap法建立了方差成分的得分检验。本文的研究与上述文献的区别在于：（I）上述研究主要针对的是纵向数据，且这些数据在各水平内是相关的，而模型（1）事实上应用在看上去独立的基于总体人群设计的遗传数据；（II）对于本文的似然比检验，同时采用置换和bootstrap法，且采用相对稳健的非参数bootstrap法而不是参数bootstrap法；（III）将基于重抽样的方法与其他方法（基于模拟的算法）进行比较［39］，结果表明重抽样方法更有效，虽然计算负荷更重；（IV）采用了有效的近似方法来提高计算效率。最后，有待进一步研究将其他方法（如，基于参数bootstrap的得分检验［52］）运用到本文的研究中并进行比较。

［1］Wu MC，Kraft P，Epstein MP，et al．Powerful SNP-Set Analysis for Case-Control Genome-wide Association Studies．American Journal of Human Genetics，2010，86（6）：929-942．

［2］Cai T，Lin X，Carroll RJ．Identifying genetic marker sets associated w ith phenotypes via an efficient adaptive score test．Biostatistics，2012，13（4）：776-790．

［3］Maity A，Sullivan PF，Tzeng Ji．Multivariate Phenotype Association Analysis by Marker-Set Kernel Machine Regression．Genetic Epidem iology，2012，36（7）：686-695．

［4］Schifano ED，Epstein MP，Bielak LF，et al．SNP Set Association A-nalysis for Fam ilial Data．Genetic Epidem iology，2012，36（8）：797-810．

［5］Dai H，Zhao Y，Qian C，et al．Weighted SNP Set Analysis in Genome-W ide Association Study．PLoSONE，2013，8（9）：e75897．

［6］Huang YT，Lin X．Gene set analysis using variance component tests．BMC Bioinformatics，2013，14（1）：210．

［7］Jiao S，Hsu L，Bézieau S，et al．SBERIA：Set-Based Gene-Environment Interaction Test for Rare and Common Variants in Complex Diseases．Genetic Epidem iology，2013，37（5）：452-464．

［8］Wu MC，Maity A，Lee S，etal．KernelMachine SNP-Set Testing Under Multiple Candidate Kernels．Genetic Epidemiology，2013，37（3）：267-275．

［9］Balding D．A tutorial on statisticalmethods for population association studies．Nature Reviews．Genetics，2006，7（10）：781-791．

［10］Prescott NJ，Lehne B，Stone K，et al．Pooled Sequencing of 531 Genes in Inflammatory Bowel Disease Identifies an Associated Rare Variant in BTNL2 and Implicates Other Immune Related Genes．PLoSGenetics，2015，11（2）：e1004955．

［11］Liu D，Lin X，Ghosh D．Semiparametric Regression of Multidimensional Genetic Pathway Data：Least-Squares Kernel Machines and Linear M ixed Models．Biometrics，2007，63（4）：1079-1088．

［12］Tzeng J，Zhang D．Haplotype-based association analysis via variancecomponents score test．American Journal of Human Genetics，2007，81（5）：927-938．

［13］Kwee L，Liu D，Lin X，etal．A Powerful and Flexible Multilocus Association Test for Quantitative Traits．American Journal of Human Genetics，2008，82（2）：386-397．

［14］Liu D，Ghosh D，Lin X．Estimation and testing for the effect of a genetic pathway on a disease outcome using logistic kernelmachine regression via logistic m ixed models．BMC Bioinformatics，2008，9（1）：292．

［15］Tzeng J，Zhang D，Chang SM，et al．Gene-trait sim ilarity regression formultimarker-based association analysis．Biometrics，2009，65（3）：822-832．

［16］Wu MC，Lee S，Cai T，etal．Rare-Variant Association Testing for Sequencing Data with the Sequence Kernel Association Test．American Journal of Human Genetics，2011，89（1）：82-93．

［17］Self SG，Liang KY．Asymptotic Properties of Maximum Likelihood Estimators and Likelihood Ratio Tests under Nonstandard Conditions．JAM STAT ASSOC，1987，82（398）：605-610．

［18］Stram DO，Lee JW．Variance Components Testing in the Longitudinal M ixed Effects Model．Biometrics，1994，50（4）：1171-1177．

［19］Liang KY，Self SG．On the Asymptotic Behaviour of the Pseudolikelihood Ratio Test Statistic．JRoy Stat Soc，1996，58（4）：785-796．

［20］Efron B，Tibshirani R．An Introduction to the bootstrap．New York：Chapman and Hall，1993．

［21］Davison AC，Hinkley DV．bootstrap Methods and Their Application．Cambridge：Cambridge University Press，1997．

［22］Good P．Permutation，Parametric，and bootstrap Tests of Hypotheses．3 edition．New York：Springer，2005．

［23］Efron B．The Jackknife，the bootstrap and Other Resampling Plans．Philadelphia：Society for industrial and applied mathematics，1982．

［24］Han F，Pan W．A data-adaptive sum test for disease association w ith multiple common or rare variants．Human Heredity，2010，70：42-54．

［25］Lin D．An efficientMonte Carlo approach to assesssing statistical significance in genom ic studies．Bioinformatics，2005，21（6）：781-787．

［26］Madsen BE，Browning SR．A Groupw ise Association Test for Rare Mutations Using a Weighted Sum Statistic．PLoS Genetics，2009，5（2）：e1000384．

［27］Lee S，Emond MJ，Bamshad MJ，et al．Optimal Unified Approach for Rare-Variant Association Testing w ith Application to Small-Sample Case-ControlWhole-Exome Sequencing Studies．American Journal of Human Genetics，2012，91（2）：224-237．

［28］Ferkingstad E，Holden L，Sandve GK．Monte Carlo nullmodels for genom ic data．Statistical Science，2015，30（1）：59-71．

［29］Lin D，Tang Z．A General Framework for Detecting Disease Associations w ith Rare Variants in Sequencing Studies．American Journal of Human Genetics，2011，89（3）：354-367．

［30］Laird NM，Ware JH．Random-effects models for longitudinal data．Biometrics，1982，38（4）：963-974．

［31］Littel R，M illiken GA，Stroup WW，et al．SAS for mixed models．SAS Institute Inc．Cary，NC，2006．

［32］Verbeke G，MolenberghsG．Linearmixedmodels for longitudinal data．New York：Springer，2009．

［33］Pinheiro J，Bates D，DebRoy S，et al．nlme：Linear and Nonlinear M ixed Effects Models．R package version 3．1-113．2013．

［34］R Core Team．R：A language and environment for statistical computing．R Foundation for Statistical Computing，Vienna，Austria．URL http：//www．R-project．org/，2014．

［35］Molenberghs G，Verbeke G．Likelihood Ratio，Score，and Wald Tests in a Constrained Parameter Space．Am Stat，2007，61（1）：22-27．

［36］Pinheiro JC，BatesD．M ixed-EffectsModels in S and S-PLUS，2nd edition．New York：Springer，2009．

［37］Kuo BS．Asymptotics of ML estimator for regression models with a stochastic trend component．Economet Theor，1999，15（1）：24-49．

［38］Claeskens G．Restricted likelihood ratio lack-of-fit tests using mixed splinemodels．JR Stat Soc B，2004，66（4）：909-926．

［39］Crainiceanu CM，Ruppert D．Likelihood ratio tests in linear mixed modelswith one variance component．J Roy Stat Soc B，2004，66（1）：165-185．

［40］Lehmann EL，Romano JP．Testing statistical hypotheses，Third edition．New York：Springer，2006．

［41］Greven S，Crainiceanu CM，Küchenhoff H，et al．Restricted Likelihood Ratio Testing for Zero Variance Components in Linear M ixed Models．JComput Graph Stat，2008，17（4）：870-891．

［42］Davies RB．Algorithm AS 155：The Distribution of a Linear Combination of chi-2 Random Variables．JR Stat Soc C，1980，29（3）：323-333．

［43］Zhang R，Zhao Y，Chu M，et al．A Large Scale Gene-Centric Association Study of Lung Function in New ly-Hired Female Cotton Textile Workers w ith Endotoxin Exposure．PLoSONE，2013，8（3）：e59035．

［44］Barrett JC，Fry B，Maller J，et al．Haploview：analysis and visualization of LD and haplotype maps．Bioinformatics，2005，21（2）：263-265．

［45］Zeng P，Zhao Y，Liu J，et al．Likelihood Ratio Tests in Rare Variant Detection for Continuous Phenotypes．Annals of Human Genetics，2014，78（5）：320-332．

［46］Patterson HD，Thompson R．Recovery of interblock information when block sizes are unqual．Biometrika，1971，58（3）：545-555．

［47］Harville DA．Maximum Likelihood Approaches to Variance Component Estimation and to Related Problems．JR Stat Soc B，1977，72（358）：320-338．

［48］Faraway JJ．Extending the linear model w ith R：generalized linear，m ixed effects and nonparametric regressionmodels．New York：Chapman＆Hall/CRC，2005．

［49］Samuh MH，Grilli L，Rampichini C，et al．The Use of Permutation Tests for Variance Components in Linear M ixed Models．Commun Stat-Theor M，2012，41（16-17）：3020-3029．

［50］Fitzmaurice GM，Lipsitz SR，Ibrahim JG．A Note on Permutation Tests for Variance Components in Multilevel Generalized Linear M ixed Models．Biometrics，2007，63（3）：942-946．

［51］Lee OE，Braun TM．Permutation Tests for Random Effects in Linear M ixed Models．Biometrics，2012，68（2）：486-493．

［52］Sinha SK．Bootstrap tests for variance components in generalized linearm ixed models．Can JStat，2009，37（2）：219-234．

（责任编辑：郭海强）

国家自然科学基金项目（81402765）；国家统计局统计科学研究项目（2014LY112）

1．徐州医科大学公共卫生学院流行病与卫生统计学教研室（221004）

2．南京医科大学公共卫生学院生物统计学系

△通信作者：曾平，E-mail：zpstat＠xzhmu．edu．cn