基于纤维垫渗滤的细小颗粒留着三维模型

基于纤维垫渗滤的细小颗粒留着三维模型

细小颗粒通常通过筛分留着在纤维垫中。迄今为止，尚未有理论将纤维和纤维垫性能与预测性留着模型结合在一起。该研究开发的多层分析留着模型，通过建模预测了颗粒穿过一连串非常薄的纤维垫时在纤维垫内的留着情况。使用人造丝纤维垫过滤粒径5～75 μm色粉颗粒的悬浮液。只有在颗粒直径与纤维直径之比增大至2.0（人造丝纤维垫数据集内的上限）时，模型预测结果才接近实验数据。同时使用模拟的纤维垫（通过该纤维垫，4～20 mm珠子滴落），采用试验方式在宏观程度上确定了留着情况。对于所有的宏观实验数据，颗粒直径至少是纤维直径的2.2倍，这解释了由这些试验得到的结果更加贴近模型预测结果。通过建模模拟了细小颗粒的留着，将模型预测结果与试验结果对比，证明了在某种程度上即使非常小的颗粒也可通过筛分留着在纤维垫中。

鉴于各种原因，必须将悬浮固体颗粒（包括油墨和填料颗粒）从纸浆中洗涤掉，尤其是在纸张的回收利用过程中。有关细小颗粒通过筛分留着在纤维垫中的文献中相关理论并不多。

有研究者提出，多孔过滤介质可以通过3种机理捕捉小颗粒：表面拉紧、深度拉紧和吸附（以下分别称作“纤维垫表面捕捉”、“内部筛分捕捉”和“纤维表面捕捉”），见图1。

图1 颗粒捕捉机理

“纤维垫表面捕捉”在几乎所有的通往垫的小孔直径均比颗粒粒径小时发生。这导致颗粒积聚在纤维垫的面向流动方向的表面上，即形成滤饼。“内部筛分捕捉”在一些内部通道不能使平均颗粒尺寸的颗粒通过（从而颗粒被从贯穿纤维垫深度的通道中滤出）时发生。“纤维表面捕捉”通常在比纤维直径或孔直径小很多的颗粒与纤维碰撞，并通过动电和范德瓦尔斯力留着时发生。这被确认为造纸过程中，填料（粒径＜1 μm）在纤维垫中留着的主要机理。

1 留着建模的统计几何学方法

有研究者推导得出了证明平面中随机线形成的多边形的面积，平均来说，与任一边长的平方成比例的解析表达式。他们得出结论：纸张的孔尺寸分布不受纤维长度和纤维宽度影响，因为宽纤维完全堵塞了一些较小的孔，而较大孔的尺寸减小，因此孔尺寸分布保持不变。这意味着，多孔性减小，但是对于任何尺寸的颗粒，过滤效率是相同的。研究人员通过使用不含细小组分的未磨浆纤维抄制定量为2.5 g/m2的手抄片证实了其分析结果。

也有研究者推导得出了通过纤维垫渗滤的颗粒遇到直径不大于dp（颗粒直径或当量直径）的孔的可能性的表达式。他们一般采纳上述研究者的处理方法。他们将孔当量直径模型的预测结果与文献中的孔尺寸分布实验数据进行了比较。2个研究小组均得到如下结论：孔的分布呈对数正态分布，并且纤维宽度不影响二维（2D）纤维垫的孔尺寸分布。

另有研究者使用多边形内切圆的尺寸分布开发了2D纤维垫内留着情况的解析表达式；留着率，作为线密度（λ）的函数，表示为每单位垫观察窗直径中线（纤维）的数量。纤维垫观察窗直径（dw）用于实现泊松线场；泊松线场没有线（纤维）终止于dw内。他们证明了，小于给定大小的内切圆面积与总内切圆面积之比可以写为：

式中，无量纲变量φ=λdp。通过模拟对留着情况的分析模型进行了验证。多位研究者提出，实际厚度的纤维垫[即三维（3D）纤维网络]可以通过数学方式，描述为一叠2D纤维网络。其中有位研究者认为3D纤维网络中纤维间相互作用的解析表达式“不适宜”。

2 之前的实验研究

造纸行业文献中报道的试验工作的绝大多数讨论的是粒径小于1～3 μm颗粒的留着。这些文献通常使用多孔活塞渗滤装置。在垫孔隙率恒定的情况下，每单位垫厚度的水力阻力载荷恒定，但是总阻力荷载累积。这意味着，在流体进入垫的位置，总阻力荷载为零，并且在流体进入点处，等于垫面积与整个垫厚度上流体压降的乘积。如果该垫采用机械方式被压缩，而不是水力阻力荷载通过一个多孔活塞渗滤装置对其进行压缩，则水力阻力荷载将不会进一步对其进行压缩。合适压缩后的垫保持已知厚度，并且因受到流体阻力荷载，孔隙率在整个垫厚度上一致。

研究者证明，这可以通过数学方式表示为：

式中：d[P]为整个垫厚度增量d t上颗粒浓度的变化；k为留着系数。方程式（2）可以重新整理和合并得到更为方便的形式：

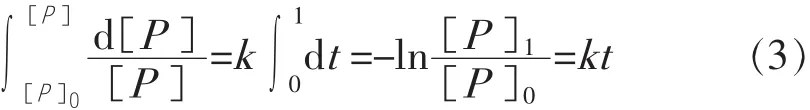
如果所有颗粒浓度表示为进入浓度[P]0的分数，则表达式简化为ln[P]t=kt。鉴于留着率=1-[P]t，方程式（3）重新整理并简化为试验留着率方程式：

尚未见有用方程式（4）描述较大颗粒通过内部筛分进行留着情况的报道。

有研究者在45℃温度和pH=8.5下，在一个多孔活塞装置中，使用商品漂白硫酸盐云杉浆垫（去除了100目细小组分），以10%浆浓进行了苯胺印刷油墨和钙皂凝集颗粒（dp=0.5～3.0 μm）的置换洗涤。他们确定了表面吸引力是油墨和钙皂凝集颗粒留着的主要原因。通过筛分发生的留着作用非常小。虽然该研究工作未能将纤维垫性能和dp与颗粒的留着作用之间建立联系，但却是少有的悬浮体的置换洗涤公开结果之一。

多项研究均报告了在控制相对不严格环境下，较大颗粒的渗滤结果，包括在对通过表面吸引力进行的留着作用不利的化学条件下，手抄片成形过程中发生的留着。所有这些参考文献表明，通过筛分进行的留着作用较小，但是对粒径dp小至2.5 μm（通常留着率=0.01～0.03）的颗粒非常重要；并且表明，在定量为20～60 g/m2的手抄片成形过程中，留着率随lg（dp）呈线性增大。由于在手抄片抄制过程中，纤维垫孔隙率不恒定，因此该信息只适用于与类似的手抄片研究作对比。

3 多层分析留着模型开发

3D纤维垫可以用一系列2D纤维垫模拟，见图2。

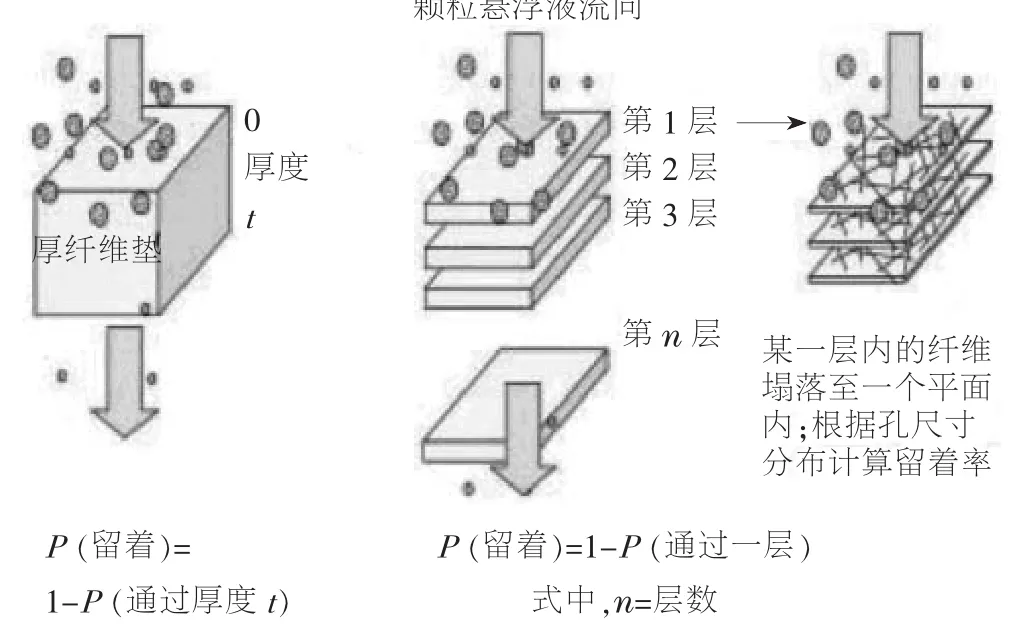
图2 用一系列薄纤维垫模拟厚纤维垫

一层内的留着率可以通过将该层内的所有纤维投影到一个平面内，根据方程式（1）计算得到。假设各层相互独立，并假定层厚度tl=dp，因为在纤维垫厚度方向上相互距离超过dp的纤维无法相互作用，从而将直径=dp的颗粒留住。n=t/dp层（每层的厚度=tl=dp）上的留着率可以写为：

实际纤维垫的λ和λl值（分别表示纤维垫内和纤维垫某一层内的纤维浓度）可以根据基本的纤维、纤维垫和颗粒性能计算。整个厚度=t上纤维的总数量（在此情况下，纤维段理论上可以用一个圆形观察窗内的弦线表示）可以通过用直径=dw的观察窗内的总纤维长度除以平均弦线长度=dwπ/4计算得到：

式中，ρf=截面为圆形的纤维的密度。在λ的计算过程中，dw内的纤维段数相当于Nf。用方程式（6）除以dw，乘以一层的层厚度分数（对于λl，层厚度分数为dp/tm），然后再进行简化，即得到λ和λl的定义：

和

式中，BW=厚度为t的纤维垫的定量。注意，方程式（7）和（8）的简化形式中未出现dw。这是因为某一层或整个纤维垫内的纤维浓度不受观察窗直径的选择影响。观察窗直径在概念上仅适用于实际纤维垫。

多层分析留着模型的基础是较厚纤维垫可以用一系列2D纤维垫模拟，每一个2D纤维垫表示的厚度为tl=3D纤维垫的dp。总体来说，这可以称作基础层概念。

可以通过调整使实验数据与通过多层模型预测的留着率值拟合，测试该概念在整体意义上的拟合度。如果针对dp的某些值，以通过2D分析模型[方程式（1）]和实验模型[方程式（4）]预测的单一一层的留着率值和t为坐标绘制曲线，则模型只有在t的唯一值（基础层厚度；理想情况下，当层厚度t=dp时）处，预测得到的留着率值相同。如果对实验数据可知的dp的所有值，重复该过程，则可以针对一系列dp值，以留着率预测值相同时的垫厚度和dp为坐标绘制曲线。如果这些数据点落在直线t=dp上或附近，则可以断定，2D留着率分析模型可以通过厚度t=dp的3D纤维垫预测留着率。

研究人员通过试验方法，确定了留着系数k为-ln[P]与 t的最佳配合情况下，线性回归线的斜率。分析推导得出的可比较留着率可以通过设置使用多层分析模型[方程式（5）]等于实验模型[方程式（4）]，然后求解k[对于分析性3D模型，重新命名为k（a）]计算：

推导过程通过在tl=t=dp情况下，求解单一一层的k（a）稍微进行简化，并通过试验方法进行了验证。

4 实验方法

4.1 人造丝纤维垫渗滤试验

在多孔活塞渗滤装置中，通过之前形成的纤维垫对颗粒进行了渗滤，从而确保垫的孔隙率已知，与流体流动速率无关。多孔活塞渗滤装置如图3所示。

图3 多孔活塞渗滤装置的截面图

由于人造丝纤维化学性质与天然纤维素纤维相似，因此选用了截面为圆形的人造丝纤维进行渗滤试验。与疏水性较大的纤维（比如聚酯）相比，人造丝纤维比较容易分散在水性悬浮液中。

选用色粉颗粒作为本研究的悬浮固体颗粒。将色粉颗粒研磨，并通过空气分类至所需的尺寸范围，但是不对它们进行加热熔化处理，因为它们将以普通方式使用。本研究选用的色粉为含10%～15%炭黑的苯乙烯/丙烯酸盐聚合物。颗粒尺寸范围较宽，颗粒平均尺寸比市场上可买到的色粉大很多。

所有渗滤使用去离子水，在温度20℃下进行；所使用的去离子水用NaOH溶液将pH调节至10.0。渗滤过程中添加了浊点为74℃、亲水亲油平衡值（HLB）为13∶1、临界胶束浓度（CMC）为0.001 8%的非离子表面活性剂，用于消去通过表面吸引力产生的留着作用。废水悬浮液样品使用孔隙大小为0.8 μm的47 mm微滤器膜（GN-4测量用混合纤维素醚膜）过滤。膜在干燥后，用蓖麻油清洗干净，图像使用透色光，在1.75 μm/像素校准度下进行分析。数据使用5 μm当量直径数据箱进行报告；报告每一数据箱中点处的颗粒尺寸。

使用3种直径（df=0.016 8、0.022 8和0.048 5 mm）、定量（BW=218、872和1 744 g/m2）和孔隙率值（ε= 0.80、0.85和0.90）均不同的随机取向和偏倚取向人造丝纤维垫对粒径5～75 μm的色粉颗粒悬浮液进行了渗滤。本文所涉及的所有渗滤过程的表面速度均为10 mm/s。

4.2 宏观渗滤试验

物理模型的厚度约为10 mm。使用这些物理模型在此厚度（孔隙率=0.967 6）和在一个压缩架（图4）内压缩至所述厚度的一半（孔隙率=0.935 0）后进行渗滤。也使用了通过将多个随机取向或偏倚取向物理模型堆叠在一起得到的较厚垫进行了渗滤。渗滤在空气中，使用直径dp=4～20 mm的珠子进行。珠子分布在一个网格上，以确保在整个垫模型区域上的分布均匀。

图4 宏观渗滤试验装置示意图

5 试验结果

5.1 宏观结果

将宏观模型回归至方程式（3），以确定留着系数k的试验值（图5）。图中列出了留着系数（经过原点的回归线的斜率）和每一条回归线的R2值（斜率=k的试验值）。

图5 随机取向模拟纤维垫在λ=0.0125t（1/mm2）（ε=0.9679）情况下的宏观渗滤数据（-1n[P]对t）的回归

图6为用于确定对于特定的颗粒直径，分析模型[方程式（1）]与实验模型[方程式（4）]预测的留着率值相同时的垫厚度的图解法实例。

该垫厚度是基础层厚度，理想情况下为t=dp。针对所有宏观渗滤数据重复进行了该程序（28次图解分析），以所得到的基础层厚度值和dp为坐标绘制了曲线图，见图7。

考虑到垫面积较小和所渗滤的珠子的数量有限，由图7可以看出，数据点的离散度较高，这是在意料之中的。

图6 λ=0.0125t（1/mm2）情况下，随机纤维垫的宏观渗滤数据、实验模型和分析模型的留着率-垫厚度关系曲线（珠子dp=16 mm）

图7 所有宏观渗滤实验数据与二维分析模型数据一致情况下的基础层厚度-颗粒直径关系

现在可以方便地假设基础层厚度等于颗粒直径，以便将通过多层分析模型[方程式（5）]预测的留着数据与通过试验得到的留着数据进行对比（图8）。拟合度非常接近平价关系线。经过原点的最佳拟合线的斜率为1.023，R2值为0.853 9。该值仅仅稍小于通过相同数据的回归确定，用于确定留着系数k的平均R2值（图5）。

5.2 人造丝纤维垫渗滤结果

图9（df=0.022 8 mm，孔隙率=0.85）、图11（df= 0.048 5 mm，定量=872 g/m2）和图13（定量=872 g/m2，孔隙率=0.85）给出了原始留着数据，以证明定量、孔隙率和纤维直径的影响。为了进行比较，图10（df= 0.022 8 mm，孔隙率=0.85）、图12（df=0.048 5 mm，定量=872 g/m2）和图14（定量=872 g/m2，孔隙率=0.85）给出了通过多层分析模型和方程式（10）预测的可比较留着数据值。

图8 留着率实验数据——多层分析模型预测留着率关系图（所有宏观渗滤数据）

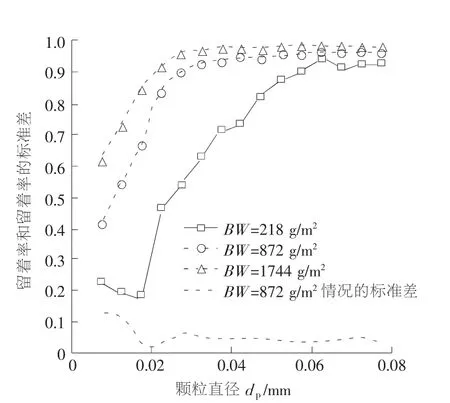
图9 随机取向人造丝纤维垫的留着率和留着率的标准差与dp和定量的影响之间的关系曲线

图10 多层分析模型预测留着率与dp和定量的影响之间的关系曲线图

图11 随机取向人造丝纤维垫的留着率和留着率的

图12 多层分析模型预测留着率与dp和孔隙率的影响之间的关系曲线图

图13 随机取向人造丝纤维垫的留着率和留着率的标

图14 多层分析模型预测留着率和留着率的标准差与dp和纤维直径的影响之间的关系曲线

将人造丝纤维垫渗滤数据回归至方程式（3），以标准差与dp和孔隙率的影响之间的关系曲线准差与dp和纤维直径的影响之间的关系曲线通过试验方式，确定留着系数k值。在进行该步骤前，进行了数据修正。图13的数据清楚地表明，随着dp增大，留着率渐近地接近一个比1.0略小的值。这可能是由于渗滤过程中，通过垫边缘的颗粒悬浮液发生泄漏。可以通过用该渗滤过程的所有留着率值除以数据渐近接近的留着率值加以修正。在以下情况下应用了该修正法：dp的最大的5个值的平均留着率至少为0.90，并且针对dp的最大的5个值，以留着率和dp为坐标的曲线的最佳拟合线斜率的绝对值一致小于0.001 5时。回归中，未考虑留着率大于0.95的数据，因为纤维垫下游侧的颗粒数量不足。

如前所述，将数据整理后，确定了数据可知的所有情况的k值。以所得到的k值和dp为坐标绘制曲线，如图15所示。对于dp＞22.5 μm的情况，各k值的R2值一般大于0.80。

图15 所有随机取向人造丝纤维垫渗滤过程的k-dp关系曲线

数据曲线和模型预测结果（图9～15）的趋势正如所预期的，留着率随dp和定量增大而增大，并随着df和孔隙率减小而增大。但是，多层分析模型未能很好地预测留着率的绝对值，尤其是在dp值较小情况下。多层分析模型在选定参数范围内预测留着率的能力可以用比值k/k（a）表示。当该比值接近1.0时，多层分析模型能够精确地预测留着率值。针对图15中曲线绘制使用的所有k值，以比值k/k（a）和dp为坐标绘制了曲线，如图16所示。

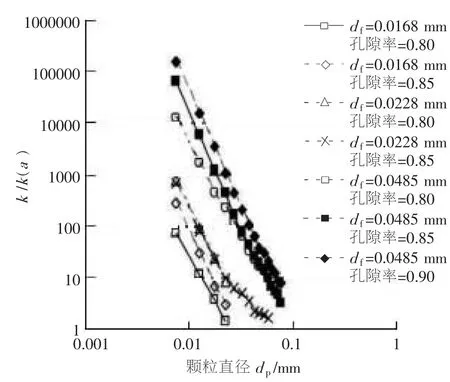
图16 图15中所示的所有k值和根据方程式（9）计算的对应k（a）值的k/k（a）-dp关系曲线

图16揭示了纤维直径与k/k（a）接近1.0时的颗粒直径之间的紧密相关关系。这表明，确定使通过试验方式确定的留着率与通过多层分析模型预测的留着率合理一致的条件是有可能的。如果比值dp/df比较关键，则在以k/k（a）和dp/df，而不是dp为坐标绘制曲线图时，图16各分开的线应塌落（collapse）到单一数据序列上。

图17显示了图15所示的所有k值和根据方程式（9）计算的对应k（a）值的k/k（a）-dp/df关系曲线[k/k（a）数据也可以由所有宏观渗滤过程获知。对于纤维垫取向，R=随机，B=偏倚]。

图17表明，数据发生严重塌落，但是并未塌落到单一数据序列上。这表明，k/k（a）的变化在很大程度上可以，但并不能完全由比值dp/df解释。遗憾地是，由人造丝纤维垫渗滤试验得到的数据几乎完全超出了k与k（a）之间存在合理对应关系的范围。从宏观渗滤实验数据到人造丝纤维垫数据（也列在图17中），可以进一步看出k/k（a）与dp/df之间的强依赖关系。很显然，只有在dp/df增大超过1.0时，k/ k（a）才接近1.0。这一现象的直观解释是，当df变得与dp相比可忽略时，k/k（a）接近1.0。

图17 图15中所示的所有k值和根据方程式（9）计算的对应k（a）值的k/k（a）-dp/df关系曲线

针对所有随机取向人造丝纤维垫渗滤数据，以通过实验模型[方程式（4）][k的值由方程式（9）所示模型预测]预测的留着率和人造丝纤维垫试验留着率为坐标绘制曲线，如图18所示。

图18 随机取向人造丝纤维垫的留着率实验数据与通过实验模型[方程式（4）]预测的留着率之间的关系

正如预期的，对于dp值较小的情况，残差倾向于较大，因为对于dp值较小的情况，留着率的标准差高很多。

6 结论

多孔活塞渗滤装置允许人造丝纤维垫在已知和恒定孔隙率下进行渗滤，从而可以探索颗粒和纤维直径、孔隙率与留着率之间的关系。在本研究中，多孔活塞装置使用的颗粒粒径远大于之前报道研究中使用的颗粒，因此，留着的主要机理为内部筛分。粒径大小在5～10 μm范围内的大量颗粒通过筛分留着在商业常见定量和纤维直径纤维垫中，这与最近的研究结论是一致的。

宏观渗滤试验，虽然比较简陋，但是允许厚度接近颗粒直径的纤维垫进行渗滤，这对微观纤维而言是不实际的。如果只知道宏观或只知道人造丝纤维垫试验结果，或许还不能注意到k/k（a）与dp或与dp/df的关系趋势。多层分析模型只有在dp的值比df的值大很多的情况下，才可以以合理的精确度预测通过筛分发生留着的留着率。遗憾地是，这意味着，这对通常的造纸行业应用场合不是很实用；在通常造纸行业应用场合中，颗粒尺寸常常基本等于或小于纤维直径。这可能是由于2D分析模型假设纤维宽度为零。这对于预测孔尺寸分布或甚至是2D垫（即纸张）的留着率或许可以接受，但是对于预测实际纤维垫的3D层内的留着率是不合理的。看来，纤维的薄3D层与这些纤维的2D零宽度投影f的留着性能之间存在根本差异。

（马倩倩 编译）