关于不定方程x3+1=pQy2

2017-01-09赵建红

沈阳大学学报(自然科学版) 2016年6期

关键词：方程组丽江师范

赵建红

(丽江师范高等专科学校数学与计算机科学系, 云南丽江 674199)

关于不定方程x3+1=pQy2

赵建红

(丽江师范高等专科学校数学与计算机科学系, 云南丽江 674199)

丢番图方程; 整数解; 同余; 平方剩余;Legendre符号

不定方程

(1)

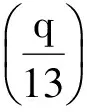
1 引理

引理1[10]设p≡7(mod24),q≡13(mod24),p,q为奇素数,则Diophantine方程组x+1=3pqu2,x2-x+1=3v2,gcd(u,v)=1当p=7,q=13时的方程除平凡解(x,u,v)=(1,0,±1)外还有非平凡解(x,u,v)=(4367,±4,±2 521),其他情形方程组只有平凡解.

2 定理及证明

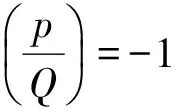
(2)

除p=13,q=7时有解(x,y)=(4367,±30 252),(-1,0)外其余方程仅有整数解(x,y)=(-1,0).

证明因为x3+1=(x+1)(x2-x+1),而gcd(x+1,x2-x+1)=gcd(x+1,3)=1或3,故方程(2)可以分解为以下8种可能的情形:

Ⅰ x+1=u2,x2-x+1=pQv2,y=uv;

Ⅱ x+1=pQu2,x2-x+1=v2,y=uv;

Ⅲ x+1=Qu2,x2-x+1=pv2,y=uv;

Ⅳ x+1=pu2,x2-x+1=Qv2,y=uv;

Ⅴ x+1=3u2,x2-x+1=3pQv2,y=3uv;

Ⅵ x+1=3pQu2,x2-x+1=3v2,y=3uv;

Ⅶ x+1=3Qu2,x2-x+1=3pv2,y=3uv;

Ⅷ x+1=3pu2,x2-x+1=3Qv2,y=3uv.

其中gcd(u,v)=1.

以下分别讨论这8种情况所给出的方程(2)的整数解的情况.

情形Ⅰ 将x+1=u2代入x2-x+1=pQv2得,(2u2-3)2+3=4pQy2,两边取模Q得

(3)

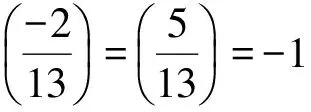
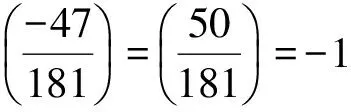
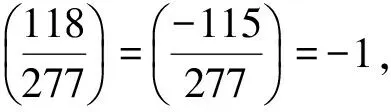
综上有该情形下方程(2)无整数解.

情形Ⅱ 解x2-x+1=v2,得x=0,1,代入x+1=pQu2均不成立,故方程(2)无整数解.

情形Ⅳ 因为p≡7(mod24),有x=pu2-1≡3,6,7(mod8),则x2-x+1≡3,7(mod8).又Q=13,109,181,229,277,421,则有Qv2≡1(mod8),矛盾.故该情形下方程(2)无整数解.

情形Ⅴ 因为x=3u2-1≡2,3,7(mod8),则x2-x+1≡3,7(mod8).又p≡7(mod24),Q=13,109,181,229,277,421,则pQ≡3(mod8),则3pQv2≡1(mod8),矛盾.故该情形下方程(2)无整数解.

情形Ⅵ 因为p≡7(mod24),Q=13,109,181,229,277,421≡13(mod24),故由引理1知方程组x+1=pu2,x2-x+1=Qv2仅当p=7,Q=13时除平凡解(x,u,v)=(1,0,±1)外还有非平凡解(x,u,v)=(4367,±4,±2521),其方程组只有平凡解(x,u,v)=(1,0,±1).在该情形下方程(2)除p=13,q=7时有解(x,y)=(4 367,±3 0252),(-1,0)外其余方程仅有整数解(x,y)=(-1,0).

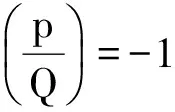
综上所述定理成立.

[ 1 ] 柯召,孙琦. 关于丢番图方程x3±1=3Dy2[J].四川大学学报(自然科学版), 1981,18(2):1-5.(KEZ,SUNQ.OntheDiophantineequationx3±1=3Dy2[J].JournalofSichuanUniversity(NaturalScienceEdition), 1981,18(2):1-5.)

[ 2 ] 柯召,孙琦. 关于丢番图方程x3±1=Dy2[J].中国科学, 1981,24(12):1453-1457. (KE Z, SUN Q. On the Diophantine equationx3±1=Dy2[J].Scientia Sinica Mathematica, 1981,24(12):1453-1457.)

[ 3 ] 杜先存,管训贵,杨慧章. 关于不定方程x3+1=91y2[J].内蒙古师范大学学报(自然科学汉文版), 2013,42(4):397-399. (DU X C,GUAN X G,YANG H Z. On the indefinite equationx3+1=91y2[J]. Journal of Inner Mongolia Normal University( Natural Science Edition), 2013,42(4):397-399.)

[ 4 ] 杜先存,万飞,杨慧章. 关于丢番图方程x3±1=1 267y2的整数解[J]. 数学的实践与认识, 2013,43(15):288-292. (DU X C,WAN F,YANG H Z. On the Diophantine equationx3±1=1 267y2[J]. Mathematics in Practice and Theory, 2013,43(15):288-292.)

[ 5 ] 杜先存,管训贵,李玉龙. 关于Diophantine方程x3+1=13qy2的整数解[J]. 南京师大学报(自然科学版), 2015,38(4):103-105. (DU X C,GUAN X G,LI Y L. The integer solution of the Diophantine equationx3+1=13qy2[J]. Journal of Nanjing Normal University (Natural Science Edition), 2015,38(4):103-105.)

[ 6 ] 管训贵,杜先存. 关于丢番图方程x3+1=13py2的整数解[J]. 贵州大学学报(自然科学版), 2014,32(2):36-38. (GUAN X G,DU X C. On the Diophantine equationx3+1=13py2[J]. Journal of Guizhou University(Natural Science), 2014,32(2):36-38.)

[ 7 ] 管训贵,杜先存. 关于Diophantine方程x3±1=pqy2[J]. 安徽大学学报(自然科学版), 2014,38(1):29-35. (GUAN X G,DU X C. On the Diophantine equationx3±1=pqy2[J]. Journal of Anhui University(Natural Sciences), 2014,38(1):29-35.)

[ 8 ] 李润琪. Diophantine方程x3+1=PQy2的整数解[J]. 海南大学学报(自然科学版), 2015,33(3):204-207. (LI R Q. Integer solution of the Diophantine equationx3+1=PQy2[J]. Journal of Hainan University(Natural Science), 2015,33(3):204-207.)

[ 9 ] 管训贵. 关于丢番图方程x3±1=7qy2的整数解[J]. 兰州文理学院学报(自然科学版), 2014,28(2):20-24. (GUAN X G. Integer solution on the Diophantine equationx3±1=7qy2[J]. Journal of Gansu Lianhe University (Natural Sciences), 2014,28(2):20-24.)

[10] 陈进平. 关于不定方程x3+1=7py2[J]. 湛江师范学院学报, 2012,33(3):19-23. (CHEN J P. On the Diophantine equationx3+1=7py2[J]. Journal of Zhanjiang Normal College, 2012,33(3):19-23.)

【责任编辑: 肖景魁】

On Indefinite Equationx3+1=pQy2

ZhaoJianhong

(Department of Mathematics and Computer Science,Lijiang Teachers College, Lijiang 674199, China)