基于多普勒谱优化的HRWS SAR系统通道相位偏差估计算法
2017-01-09王志斌刘艳阳李真芳陈筠力
王志斌 刘艳阳 李真芳 陈筠力
基于多普勒谱优化的HRWS SAR系统通道相位偏差估计算法
王志斌①刘艳阳②李真芳*①陈筠力③
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)②(上海卫星工程研究所 上海 201109)③(上海航天技术研究院 上海 201109)
方位多通道SAR系统通过抑制多普勒模糊,能够实现高分辨率和宽测绘带(HRWS)对地观测。针对通道间幅相偏差会导致成像结果中出现目标模糊分量的问题,该文提出一种通道相位偏差估计算法。该算法利用通道间相位偏差会造成多通道重构方位谱在主瓣内展宽的特性,通过优化多谱勒谱能够实现通道相位偏差的有效估计。该算法在通道相位偏差估计前不需要进行多普勒中心估计,减小了由多普勒中心估计不准引入的误差,并且在低信噪比的情况下仍然具有良好的估计性能。基于仿真数据和实测数据的实验验证了该文算法的有效性。
合成孔径雷达;高分辨率宽测绘带;多通道;数字波束形成;通道相位偏差估计;多普勒谱优化
1 引言
高分辨和宽测绘带(High-Resolution and Wide- Swath, HRWS)成像是星载合成孔径雷达(SAR)成像的发展方向,为了能够获取方位高分辨率,需要方位向小天线来获取宽方位多普勒带宽,并且要求提高脉冲重复频率(Pulse Repetition Frequency, PRF)以满足奈奎斯特采样定律,从而获取无模糊的方位多普勒谱。但是,为了获取无距离模糊的宽测绘带需要降低PRF,因此,高分辨率和宽测绘带是一对矛盾量[1]。传统的星载单通道SAR系统由于面临上述约束,难以实现HRWS成像。方位多通道系统采用数字波束形成技术(Digital Beam-Forming, DBF)能够突破上述限制[2,3],已经成为HRWS成像的有效手段。DBF解模糊要求各通道间特性一致[4,5],但是,由于制造工艺,加工环境等,通道间之间不可避免地存在通道偏差,而通道偏差的存在会降低DBF的性能。因此,为了提高方位多通道DBF的性能,需要首先进行通道偏差校正。
为解决多通道SAR成像存在的通道偏差问题,近几年来,许多学者提出了不同的解决方法。针对分布式小卫星系统,文献[6]提出了一种基于“虚拟校正源”的通道偏差校正方法,该方法将每个通道主瓣内的谱分量作为校正源,将通道间幅相偏差校正问题转换为传统的已知校正源的阵列误差估计问题。文献[7]提出了一种自适应加权最小二乘(Adaptively Weighted Least Square, AWLS)的相位偏差估计算法,该算法通过约束处理多普勒带宽外的信号能量最小,能够有效地对通道间的相位偏差进行估计。
针对通道间的相位偏差估计问题,本文提出一种基于多普勒谱优化的HRWS系统通道相位偏差估计新算法。基于通道间相位偏差的存在,将会导致重构的方位多普勒谱展宽的事实,本文从重构的多普勒谱出发,通过优化重构的多普勒谱来估计通道间的相位偏差。基于仿真数据和机载实测数据的实验验证了本文算法的有效性和性能。
2 方位多通道信号模型和通道误差模型

图1 方位多通道SAR系统对地观测示意图
通常情况下,星载SAR系统整个面板发射宽波束信号,然后,各个通道同时接收地面回波,各个通道工作于双基模式,但是,由于各个通道之间的沿航向基线很短,补偿一个常数相位后,可以等效为各个通道在各自的相位中心自发自收的单基模式。假设第通道在时刻的位置为(,0,0),为通道与参考通道之间的沿航向等效基线长度,为卫星速度。将参考通道接收的信号记为,则第通道接收的信号可以写为

(2)
每个方位多普勒单元内包含无数同锥角的场景回波,传统的星载单通道SAR系统的PRF高于方位向带宽,方位多普勒频率与锥角的余弦值为线性关系:

对于多通道SAR系统,通道间幅度误差、相位偏差以及位置误差的存在会降低DBF解模糊的性能,因此多通道解模糊成像前首先要对通道偏差进行校正。通道位置误差对多通道解模糊性能影响较小,而通道幅度误差可以通过幅度均衡的方法进行校正[18],因此,本文重点考虑通道相位偏差估计校正问题。假设第个通道与参考通道间的相位偏差为,第通道接收的信号在距离-多普勒域可以写为

(5)
其中,

(7)
(8)

(10)
(11)

3 通道相位偏差估计新方法
3.1 相位偏差估计新算法
根据式(4)-式(12)可以得出,主瓣内无模糊的多通道信号为

其中,
(14)
式(14)可以写简化为
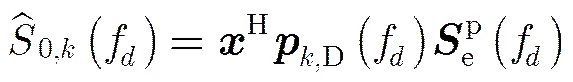
其中,
(16)

星载SAR系统通过优化方向图设计,越偏离多普勒中心处的频率能量越小,其多普勒谱分量的强度越低。由于通道相位偏差的存在,改变了多通道重构方位多普勒谱的能量分布,相比于无误差的多通道重构谱,较多的能量会分布于远离多普勒中心处,因此,通道相位偏差的存在将会导致方位多通道重构谱主瓣的展宽。一个直观的现象是方位多通道重构谱的幅度峰值会下降,从而导致重构谱的对比度降低。我们定义多普勒谱的对比度来定量描述方位谱的变化,定义式(18):
(18)
利用某机载X波段HRWS SAR系统录取的数据来说明通道相位偏差的存在对重构多普勒谱的影响,其系统参数如表1所示。
表1 某X波段机载多通道SAR系统参数

参数取值 雷达载频9.6 GHz 发射信号带宽20 MHz 距离向采样率24 MHz 脉冲重复频率500 Hz 方位向带宽280 Hz 平台速度148 m/s 相邻通道等效相位中心间距0.4 m
需要指出的是,此机载SAR系统每个通道的PRF都高于其方位向带宽,因此,每个通道获取的数据在方位谱的主瓣内是无模糊的。为了获取主瓣内有模糊的信号,我们对每个通道获取的数据进行5倍降采样处理,此时,每个通道的PRF等效为100 Hz,此时,PRF低于方位向带宽,方位多普勒谱在主瓣内会产生模糊现象。降采样处理前第1个通道无模糊的方位多普勒谱如图2中无模糊的方位谱所示,当通道间存在相位偏差时,重构的多普勒谱如图2中含通道误差的重构谱所示,通过对比我们能够明显看出,当存在通道相位偏差时,重构谱相对于第1通道无模糊谱有明显的谱展宽现象。经计算,无模糊的方位谱的最大对比度约为含通道误差重构谱的1.05倍,因此,通过约束多普勒谱主瓣的对比度最大能够估计通道间的相位偏差。
图2 通道间相位偏差对重构方位多普勒谱的影响
当观测场景内的回波信号不满足方位谱的对比度最大的分布特性时,更一般地,我们定义式(19):

根据以上分析,为了估计通道间的相位偏差,本文提出一种基于多普勒谱优化的通道相位偏差估计新方法,其中待优化的目标函数为
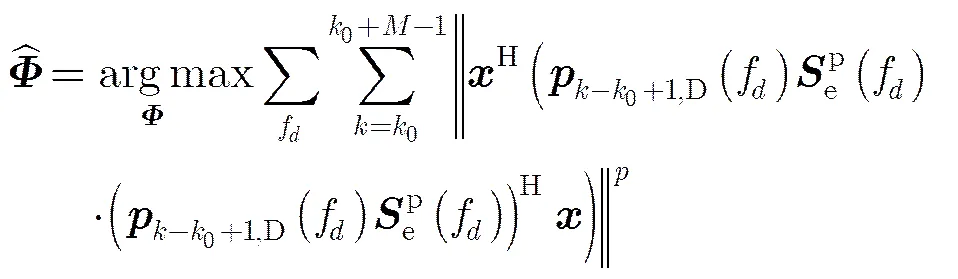
(21)
其中,

上述优化问题可以通过牛顿迭代法或者迭代的最小化过程求解[19]。本文中,简单介绍利用牛顿迭代法求解该优化问题的过程。利用牛顿迭代方法,第()迭代的值由式(23)获得
(23)
其中,
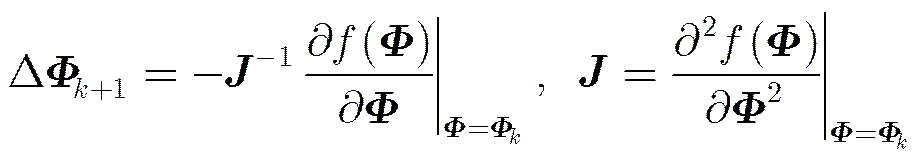
(25)
(26)

(28)
牛顿迭代的终止条件与相位偏差估计精度有关,通常情况下,越高的估计精度需要越高的运算量。
3.2 实现步骤
本文基于多普勒谱优化的方位向多通道HRWS SAR系统通道相位偏差估计算法处理流程如图3所示,主要包括以下处理步骤:
(1)将各通道的2维回波信号经方位向FFT变换至距离-多普勒域;
(2)根据步骤(1)获得的距离-多普勒域多通道信号,重构方位向多谱勒谱,构造式(20)所示的目标函数;
(3)采用牛顿迭代法或者迭代的最小化过程求解上述优化问题,提取各通道相对于参考通道的相位偏差。

图3 本文算法的处理步骤
4 实验分析与验证
4.1 仿真数据分析
本节利用仿真的星载HRWS SAR系统数据进行本文算法的性能分析,方位多通道SAR系统的仿真参数如表2所示,所选用的原始回波数据为ASAR于2010年11月6日在日本宫城地区所录取,无模糊的回波经成像处理后的SAR图像如图4(a)所示。将无模糊的信号进行方位向降采样处理能够获取存在方位多普勒模糊的多通道SAR回波,在通道之间添加固定的相位偏差(添加的误差如表3所示)构成含通道相位误差的HRWS SAR系统回波()。
表2 方位多通道SAR系统仿真参数

参数取值 载频5.4 GHz 卫星速度7541.9 m/s 方位带宽1426 Hz 多普勒中心0 通道数4 PRF442.5 Hz
表3 相位偏差估计结果

通道1通道2通道3通道4 实际相位偏差040.00-35.0020.00 相位偏差估计值039.89-35.1519.84 相位偏差估计误差0-0.110.15-0.16
(1)算法验证: 由本文算法对仿真的多通道数据进行通道相位偏差估计,得到的相位偏差估计值如表3所示,与实际仿真添加的相位偏差相比,本算法的估计误差约为。通道相位偏差校正前后的SAR图像分别如图4(b)和图4(c)所示,对比图4(b)与图4(c)可以看出,校正本文估计的通道相位偏差后,模糊信号得到了有效地抑制,验证了本文算法的有效性。
(2)本文算法性能: 下面采用Mento-Carlo实验分析本文算法在不同通道均匀度和信噪比下的性能。定义通道均匀度因子为[7]

(30)
(3)算法性能对比分析: 文献[7]依据能量分布提出了优化多普勒带宽内能量最大的相位偏差估计算法,该方法在相位偏差估计前要先进行多普勒中心估计,当缺少多谱勒中心估计或者多普勒中心估计不准时,会导致相位偏差估计失败,而本文算法优化重构的多谱勒谱,相位偏差估计前无需进行多谱勒中心估计。本节采用Mento-Carlo实验对比分析本文算法与文献[6]和文献[7]中的算法在不同信噪比下的相位偏差估计性能,性能对比如图7所示。通过图中的曲线能够看出,相对于文献[6]和文献[7]中的通道相位偏差估计算法,本文算法在低信噪比()时,具有较好的估计性能,而在高信噪比()时,各算法的相位偏差估计性能相当。
4.2 实测数据分析
我们采用与3.1节相同的机载数据来说明本文提出的基于多普勒优化的相位偏差估计算法的性能。第1通道未降采样前的方位多普勒谱如图8中无模糊的方位谱线条所示,利用RD成像算法得到第1通道聚焦后的SAR图像如图9(a)所示。

图4 仿真HRWS SAR系统通道相位偏差校正前后对比图

图5 算法估计性能随SNR变化图 图6 算法估计性能随变化图

图7 算法估计性能对比分析图 图8 通道误差校正前后的重构方位多普勒谱

图9 聚焦后的SAR图像
采用本文算法估计得到的系统各通道相对于第1通道的相位偏差分别为。校正后的方位向多普勒谱为图8中相位偏差校正后重构方位谱的线条,通过对比可知,校正后方位向多普勒谱和无模糊方位向多普勒谱的差异较小,而对比图8中校正后与校正前的方位多普勒谱(含相位偏差重构方位谱),可以看出校正后多普勒谱主瓣展宽的现象得到明显的改善。
通道相位偏差校正前聚集后的SAR图像如图9(b)所示,由图可知,图9(b)成像结果中存在许多模糊信号(特别是圆圈内标注区域)。利用本文算法校正通道间相位偏差后的聚焦SAR图像如图9(c)所示,为了更好地对比图9(b)和图9(c),我们将图9(b)和图9(c)的图像幅度分别与图9(a)的图像幅度作差,得到的差值分别如图9(d)与图9(e)所示,对比图9(d)和图9(e)可以看出,通道相位偏差校正后的SAR图像方位模糊得到了较好的抑制。
5 结论
针对星载方位向多通道HRWS SAR系统通道相位偏差校正问题,本文基于通道间的相位偏差的存在会导致方位多通道重构谱展宽的现象,提出了一种基于多谱勒谱优化的通道相位偏差估计新算法。本文方法以重构的方位向多谱勒谱为目标函数,采用牛顿迭代法或者迭代的最小化过程来优化求解得到通道间的相位偏差。基于仿真数据和实测数据的实验验证了本文算法的有效性。
参考文献
[1] Freeman A, Johnson W, Huneycutt B,. The “myth” of the minimum SAR antenna area constraint[J]., 2000, 38(1): 320-324. doi: 10.1109/36.823926.
[2] Kim J, Younis M, Prats-Iraola P,. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression[J]., 2013, 51(1): 579-590. doi: 10.1109/TGRS.2012.2201947.
[3] Gebert N, Krieger G, and Moreira A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wide-swath SAR imaging[J]., 2009, 45(2): 564-592. doi: 10.1109/TAES.2009.5089542.
[4] KRIEGER G, Gebert N, and Moreira A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J]., 2004, 1(4): 260-264. doi: 10.1109/LGRS.2004. 832700.
[5] Li Z, Wang H, Su T,. Generation of wide-swath and high-resolution SAR images from multichannel small spaceborne SAR systems[J]., 2005, 2(1): 82-86. doi: 10.1109/LGRS.2004. 840610.
[6] Li Z, Bao Z, Wang H,. Performance improvement for constellation SAR using signal processing techniques[J]., 2006, 42(2): 436-452. doi: 10.1109/TAES.2006.1642562.
[7] Liu Y, Li Z, Yang T,. An adaptively weighted least square estimation method of channel mismatches in phase for multichannel SAR systems in azimuth[J]., 2014, 11(2): 439-443. doi: 10.1109/LGRS.2013.2264771.
[8] 李银伟, 陈立福, 韦立登, 等. 基于多普勒域多通道的机载合成孔径雷达自聚焦算法[J]. 电子与信息学报, 2015, 37(4): 969-974. doi: 10.11999/JEIT140675.
LI Yinwei, CHEN Lifu, WEI Lideng,An autofocus algorithm based on Doppler-domain multichannel for airborne SAR[J].&2015, 37(4): 969-974. doi: 10.11999/JEIT140675.
[9] JIN T, QIU X, HU D,. Channel error estimation methods comparison under different conditions for multi- channel HRWS SAR systems[J].&, 2016, 4(3): 88-94. doi: 10.4236/jcc.2016. 43014.
[10] LIU B and HE J. Improved DBF algorithm for multi-channel high-resolution wide-swath SAR[J]., 2016, 54(2): 1209-1225. doi: 10.1109/TGRS.2015.2476496.
[11] 杨桃丽, 李真芳, 刘艳阳, 等. 两种星载高分辨宽测绘带 SAR 系统通道相位误差估计方法[J]. 电子学报, 2013, 41(5): 931-935. doi: 10.3969/j.issn.0372-2112.2013.05.016.
YANG Taoli, LI Zhenfang, LIU Yanyang,. Two channel phase error estimation methods for spaceborne HRWS SAR system[J]., 2013, 41(5): 931-935. doi: 10.3969/j.issn.0372-2112.2013.05.016.
[12] Yang T, Li Z, Liu Y,Channel error estimation methods for multichannel SAR systems in azimuth[J]., 2013, 10(3): 548-552. doi: 10.1109/LGRS.2012.2212878.
[13] FANG C, LIU Y, LI Z,. Clutter-cancellation-based channel phase bias estimation algorithm for spaceborne multichannel high-resolution and wide-swath SAR[J]., 2016, 13(9): 1260-1264. doi: 10.1109/LGRS.2016.2580740.
[14] 邢孟道, 孙光才, 李学仕. 用于高分辨率宽测绘带SAR系统的SAR/GMTI处理方法研究[J]. 雷达学报, 2015, 4(4): 375-385. doi: 10.12000/JR15096.
XING Mengdao, SUN Guangcai, and LI Xueshi. Study on SAR/GMTI processing for high-resolution wide-swath SAR system[J]., 2015, 4(4): 375-385. doi: 10. 12000/JR15096.
[15] 刘让, 马喜乐, 何峰, 等. MC-SAR改进正交子空间相位误差估计算法[J]. 雷达科学与技术, 2015, 13(4): 402-409. doi: 10.3969/j.issn.1672-2337.2015.04.012.
LIU Rang, MA Xile, HE Feng,. MC-SAR improved orthogonal subspace phase error estimation method[J]., 2015, 13(4): 402-409. doi: 10.3969/ j.issn.1672-2337.2015.04.012.
[16] 刘艳阳, 李真芳, 索志勇, 等. 一种星载多通道高分辨率宽测绘带 SAR 系统通道相位偏差估计新方法[J]. 电子与信息学报, 2013, 35(8): 1862-1868. doi: 10.3724/SP.J.1146.2012. 01424.
LIU Yanyang, LI Zhenfang, SUO Zhiyong,. A novel channel phase bias estimation method for spaceborne multi-channel high-resolution and wide-swath SAR[J].&, 2013, 35(8): 1862-1868. doi: 10.3724/SP.J.1146.2012.01424.
[17] 刘艳阳, 李真芳, 杨桃丽, 等. 一种单星方位多通道高分辨率宽测绘带 SAR 系统通道相位偏差时域估计新方法[J]. 电子与信息学报, 2012, 34(12): 2913-2919. doi: 10.3724/SP.J.1146. 2012.00562.
LIU Yanyang, LI Zhenfang, YANG Taoli,. A novel channel phase bias estimation method for spaceborne along- track multi-channel HRWS SAR in time-domain[J].&, 2012, 34(12): 2913-2919. doi: 10.3724/SP.J.1146.2012.00562.
[18] 张磊, 全英汇, 邢孟道, 等. 一种子空间投影的高分辨率宽测绘带SAR成像通道均衡方法[J]. 电子与信息学报, 2010, 32(1): 1-6. doi: 10.3724/SP.J.1146.2008.01821.
Zhang L, Quan Y, Xing M,. An SSP based channel calibration for high-resolution and wide-swath SAR imagery [J].&2010, 32(1): 1-6. doi: 10.3724/SP.J.1146.2008.01821.
[19] Zhang S, Xing M, Xia X,. A robust channel- calibration algorithm for the multi-channel in azimuth HRWS SAR imaging based on local maximum-likelihood weighted minimum entropy[J]., 2013, 22(12): 5294-5305. doi: 10.1109/TIP.2013. 2274387.
王志斌: 男,1989年生,博士生,研究方向为星载SAR/InSAR信号处理.
刘艳阳: 男,1987年生,工程师,研究方向为星载SAR/InSAR系统设计.
李真芳: 男,1977年生,教授,研究方向为星载SAR/InSAR系统分析与信号处理.
Phase Bias Estimation Algorithm for HRWS SAR System in Azimuth Based on Doppler Spectrum Optimization
WANG Zhibin①LIU Yanyang②LI Zhenfang①CHEN Junli③
①(,,’710071,)②(,201109,)③(,201109,)
By suppressing the Doppler ambiguity, the along-track multi-channel Synthetic Aperture Radar (SAR) system can simultaneously achieve High-Resolution and Wide-Swath (HRWS) imaging. However, the presence of unavoidable amplitude and phase bias tends to the absence of ambiguous signals in the SAR images. To address this issue, a novel phase bias estimation algorithm based on Doppler spectrum optimization is proposed. By exploiting the fact that phase bias can cause Doppler spectrum broadened, the phase bias can be successfully estimated by optimizing the Doppler spectrum. The Doppler centroid estimation can be avoided before phase biases estimation, which reduces the estimation accuracy caused by the inaccurate Doppler centroid. The proposed algorithm can achieve better performance when Signal to Noise Ratio (SNR) is low. The effectiveness of the algorithm is validated by experimental results carried out on simulated data and SAR data collected by an air- borne multi-channel system.
Synthetic Aperture Radar (SAR); High-Resolution and Wide-Swath (HRWS); Multi-channel; Digital Beam-Forming (DBF); Phase bias estimation; Doppler spectrum optimization
TN957.51
A
1009-5896(2016)12-3026-08
10.11999/JEIT161038
2016-10-08;改回日期:2016-11-28;
2016-12-14
李真芳 lzf@xidian.edu.cn
国家自然科学基金(61471276, 61601298, 61671355)
The National Natural Science Foundation of China (61471276, 61601298, 61671355)
