单个平衡点的四翼超混沌振荡器及其电路实现*

林 愿，陈爱萍

(1.湖南工程学院 电气信息学院，湘潭 411104；2.湖南工程学院 风力发电机组及控制湖南省重点实验室，湘潭 411104)

单个平衡点的四翼超混沌振荡器及其电路实现*

林 愿1，2，陈爱萍1，2

(1.湖南工程学院 电气信息学院，湘潭 411104；2.湖南工程学院 风力发电机组及控制湖南省重点实验室，湘潭 411104)

提出了一个新的四维光滑自治超混沌系统，该系统只有一个位于原点的平衡点，却能在很大范围内产生出四翼超混沌吸引子.对系统的基本动力学特性进行理论分析和数值仿真，并设计了该混沌振荡电路，实验结果表明该四翼超混沌吸引子是物理存在的.

四翼；超混沌振荡器；动力学特性；电路实现

0 引言

随着基于混沌的保密通信技术的研究和发展，对混沌系统的复杂性提出了更高要求.为了获得动力学行为更复杂的混沌系统，人们常从两个方面对混沌系统进行了改进：从构造只有一个正的Lyapunov指数的混沌系统[1]到构造具有两个正的Lyapunov指数的超混沌系统[2-4]；从构造只能产生两翼的混沌系统[5]到能产生多翼的混沌系统[6-7].虽然构造超混沌系统和多翼吸引子的文献较多，但同时具备超混沌特性和多翼拓扑结构的吸引子的文献很少.目前报道的四维光滑自治超混沌系统，一般都是有三个或五个平衡点的双翼超混沌系统.文献[8]通过引入三次项获得了四翼超混沌吸引子，但是系统实现复杂，需要多个乘法器，且具有多个平衡点.从已有文献来看，一个平衡点能产生四翼吸引子的光滑自治超混沌系统很少见.

本文提出了一个新的四维光滑自治超混沌系统，该系统只包含三个二次乘积项，实现电路简单，却有着特别的动力学特性：它只有一个平衡点，却能在很大范围内产生四翼超混沌吸引子.本文对提出的单平衡点四翼超混沌系统的基本动力学特性进行了理论分析和数值仿真，最后设计了该混沌振荡器电路，实验验证证实该系统能产生四翼超混沌吸引子.

1 提出的四维混沌系统及其动力学特性分析

提出下面简单的四维光滑自治非线性系统：

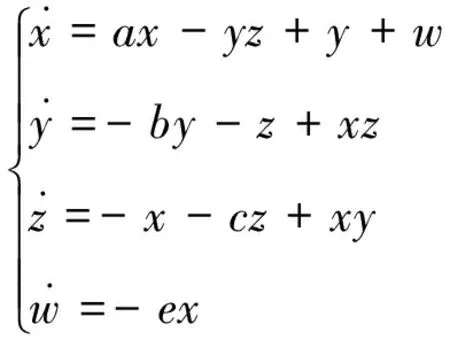
(1)

其中x、y、z、w是状态变量，a，b，c，e是正实数.我们令a=4.5,b=16,c=5, e可变化.该系统被发现在很大范围内表现出四翼超混沌特性，而且在一定条件下能观察到瞬时混沌现象.接下来，讨论该系统的一些基本动力学特性.很明显，该系统关于坐标轴、平面或者原点均不具有对称性.

1.1 耗散性及吸引子的存在性

1.2 平衡点及稳定性

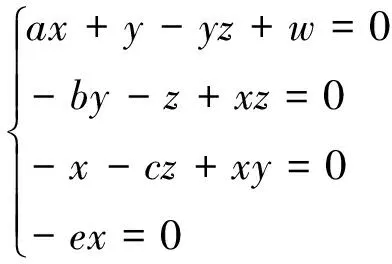
(2)

解得系统(1)只有唯一的平衡点原点(0, 0, 0, 0)，且与系数a、b、c、e无关.

为了考察系统的稳定性，需考虑其平衡点所对应的雅可比矩阵并计算其特征值，当a=4.5,b=16,c=5,e=1时得系统的特征根为：λ1=-15.9956,λ2=-5.0094,λ3=0.2338,λ4=4.2712, 表明其唯一的平衡点原点是一个不稳定的鞍点.

1.3 四翼超混沌吸引子相图

当a=4.5,c=5,b=16,e=1,初始条件为[1,1,1,1]T时，系统轨迹相图如图1所示.

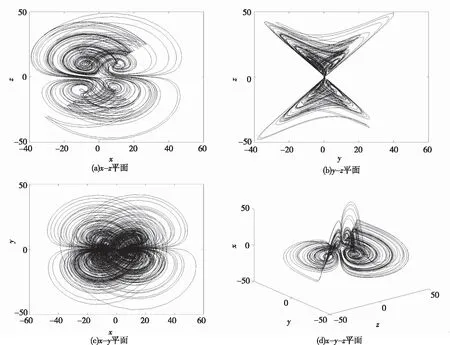
图1 四翼超混沌相三维图

我们在e∈[1,40]之间的很大范围内进行数值仿真，都能观察到四翼混沌吸引子.根据前面的技术可知该系统只有一个位于原点的平衡点，却能在很大范围内呈现出四翼混沌吸引子，这是该混沌系统的一个显著特点.

1.4 Lyapunov指数和Poincaré映射

固定a=4.5,c=5,b=16不变，当e∈[0,40]时，系统的Lyapunov指数谱如图2所示，从图2中可以看出，系统在e∈[1,40]之间的很大范围内均有两个正的Lyapunov指数，呈现出超混沌特性.

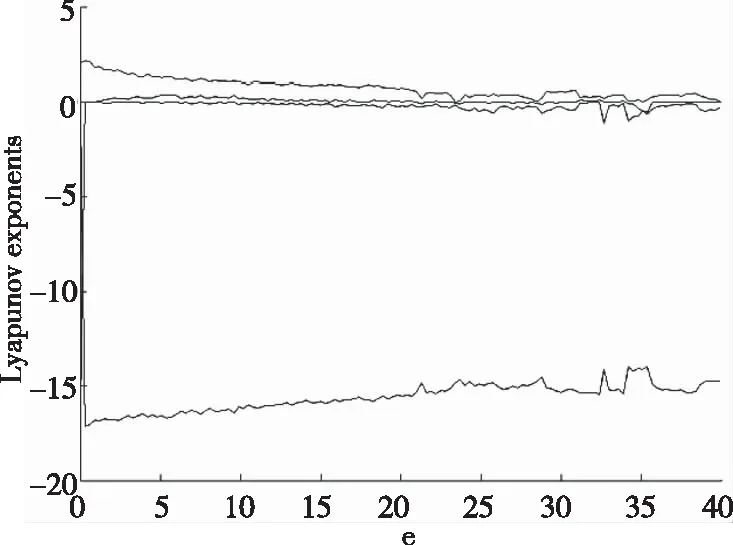
图2 系统的Lyapunov指数谱图

Poincaré映射反映了混沌分岔与可折叠特性，图3是系统(1)的Poincaré映射在不同截面的投影，可以看出该Poincaré映射存在几个不同方向分岔的分支，表明系统具有极其复杂的动力学特性，而且Poincaré映射显示其分支联结为一个单个的吸引子，这也证实了图1所示的四翼超混沌吸引子的存在性.

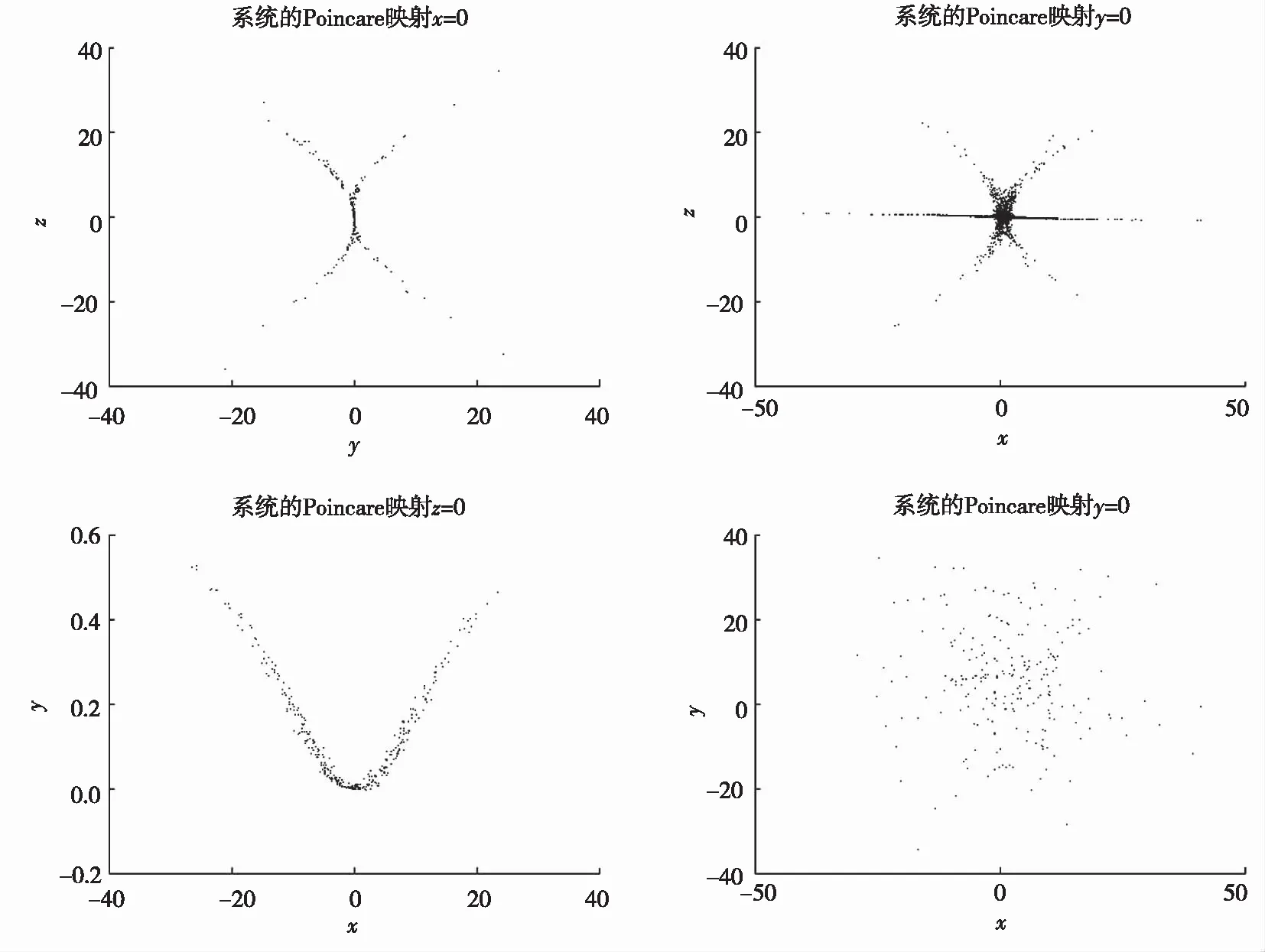
图3 Poincaré映射在x=0、 y=0、 z=0、w=0截面的投影

2 电路实现

为了验证系统(1)的混沌行为，并把该混沌系统应用到实践，设计了图4所示的混沌电路原理图.图4中选用乘法器AD633实现该超混沌系统的非线性部分，采用的运算放大器是TL082，相比文献[8]所提出的混沌系统，本文设计的四翼超混沌系统只需要三个乘法器，电路结构简单，容易实现.

该四翼超混沌系统振荡器电路方程为:

(9)

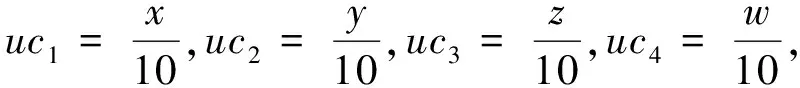
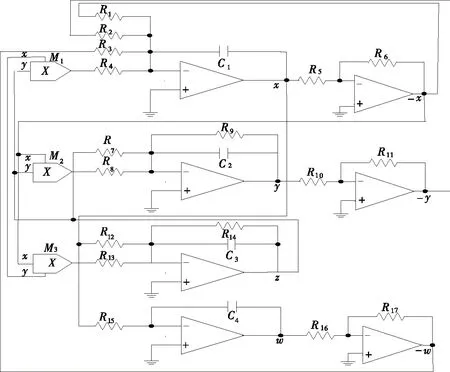
图4 四翼超混沌系统的电路图

图5 混沌系统电路实验相图

3 结论

本文提出了一个新的四维光滑自治超混沌系统，该系统只包含三个乘积项，实现电路简单，却有着特别的动力学特性：它只有一个唯一的平衡点，却能在很大范围内产生四翼超混沌吸引子.本文对系统的一些基本动力学特性进行了理论分析和数值仿真，并设计了其振荡器电路进行实验验证，实验结果表明四翼超混沌吸引子是物理存在的.

[1] 王光义, 丘水生, 许志益. 一个新的三维二次混沌系统及其电路实现[J]. 物理学报, 2006, 55 (7): 3295-3301.

[2] 罗小华, 李元彬, 罗明伟. 一种新的四维二次超混沌系统及其电路实现[J] . 微电子学, 2009, 39( 3) :398-401.

[3] Jia Li Xin, Dai Hao, Hui Meng. A New Four Dimensional Hyperchaotic Chen System and Its Generalized Synchronization [J] . Chinese Physics B, 2010, 19(10) : 100501.

[4] Si Gang Quan, Cao Hui and Zhang Yan Bin. A New Four Dimensional Hyperchaotic Lorenz System and Itsadaptive Control [J] . Chinese Physics B, 2011, 20(1) :010509.

[5] 唐良瑞, 李 静, 樊 冰. 新三维混沌系统及其电路仿真[J]. 物理学报, 2009,58(2):785-793.

[6] Qi Guo Yuan, Chen Guan Rong, Van Wyk Ma. A Four-wing Chaotic Attractor Generated From a New 3-D Quadratic Autonomous System [J]. Chaos Solitons Fractals, 2008, 38: 705-721.

[7] Sara Dadras, Hamid Reza Momeni, Guoyuan Qi. Analysis of a New 3D Smooth Autonomous System Withdifferent Wing Chaotic Attractors and Transient Chaos [J]. Nonlinear Dynamic, 2010, 62: 391-405.

[8] 胡国四.一类具有四翼吸引子的超混沌系统[J].物理学报, 2009,58(6):3734-3741.

Four-wing Hyperchaotic Oscillator with One Equilibrium and Its Circuit Implementation

LIN Yuan1,2,CHEN Ai-ping1,2

(1.College of Electrical & Information Engineering, Hunan Institute of Engineering, Xiangtan 411104, China;2.Hunan Provincial Key Laboratory of Wind Generator and Its Control, Hunan Institute of Engineering, Xiangtan 411104, China)

In this paper, a new 4-dimentional smooth autonomous hyperchaotic system is proposed. The system has only one equilibrium point at the origin, but it can generate four-wing hyperchaotic attractor over a wide range. The basic dynamic properties of 4D hyperchaotic attractor are studied by numerical and theoretical analysis. The chaos oscillator circuit is designed and it is verified that the chaotic four-wing attractor physically exist.

four-wing; hyperchaotic oscillator; dynamical property; circuit implementation

2016-05-26

湖南省教育厅科研资助项目(15C0328)；湖南工程学院青年科研重点项目(XJ1501)；湖南工程学院博士启动基金(Z).

林 愿(1977-)，女，博士，讲师，研究方向：混沌电路设计与应用.

TP309.7

A

1671-119X(2016)04-0014-04