上海沿海有效波高和最大波高关系分析

朱智慧，沈其艳，常亚楠

上海沿海有效波高和最大波高关系分析

朱智慧，沈其艳，常亚楠

（上海海洋气象台，上海201306）

运用线性回归方法，对上海沿海5个浮标站逐时的有效波高和最大波高观测资料进行分析，建立了这两种波高的回归方程，获得了估计最大波高的客观方法。对5个浮标站，一元一次回归方程都能很好地反映最大波高和有效波高的关系。最大波高通用回归方程对长江口船标资料的试报结果较好，平均绝对误差仅为0.1 m。WW3海浪模式对5个浮标站的有效波高预报与实况比较接近，利用该模式的有效波高进行最大波高的预报，预报最大波高与实测最大波高具有较好的相关性，5个浮标站平均误差最大为-0.17 m，最小为-0.05 m，平均绝对误差都为0.4 m，结果比较理想。

有效波高；最大波高；回归分析

1 引言

随着海洋经济的发展，及时提供海上的海洋环境条件，成为海洋气象预报的迫切任务。波高对于海上运输、海水养殖、海事救捞和海洋工程等生产活动，是必须考虑的重要因素。此外，在信息化时代，气象水文条件是海战环境的重要组成部分，对舰艇编队活动、军事演习、登陆作战、海洋维权等军事行动有着非常实用的价值。郑崇伟等[1-3]以钓鱼岛、黄岩岛和南海岛礁等重要岛礁海域为研究对象，利用模拟的海浪场数据，对研究海域的波候特征进行了系统研究，为海洋资源开发以及战场环境建设提供了科学指导。如今，数值预报正成为海洋气象预报的最主要手段[4-7]，数值模式输出的波高为有效波高，但是在实际中，最大波高是一个重要的参数，而在目前的海洋气象预报业务中，估计最大波高主要依靠预报员的主观判断，缺少客观定量的预报方法。文圣常等[8]从理论上分析了平均波高与其他波高的关系，由瑞利分布导出了不同波高的比值，根据他的计算，最大波高约为有效波高的1.67倍，目前，对中国近海的最大波高和有效波高的基本特征已有一些研究，刁学贤[9]根据文圣常的理论结果对青岛近岸开阔海区的波高变化进行了统计分析，李合[10]针对北部湾海区的实际波浪状况，利用测波资料计算了谱宽参数的分布规律，然后在宽谱的条件下确定了最大波高与有效波高的关系随谱宽度参量与波个数的变化规律。国外的学者Goda[11]提出最大波高可以通过将有效波高乘以1.8倍来获得，但是Kim等[12]研究指出，这种方法在没有波破碎的情况下比较适用，在有波破碎的条件下，两种波高的关系是高度非线性的，为此，他们引入了一个随机变量来描述两种波高的关系。针对海洋工程中关心的多年一遇最大设计波高和有效波高，国内外也有很多研究[13-15]，但是，这些最大设计波高的计算方法并不适用于日常海洋气象业务中的最大波高预报。因此，分析上海沿海有效波高和最大波高的关系，建立计算最大波高的客观方法，将能够为沿海各种海洋经济和军事活动提供更加准确的预报。

2 资料和方法

2.1 资料

本文所使用的资料为：

（1）上海沿海5个浮标站的实测资料，分别为长江口船标（122.53°E，31.1°N）、海礁浮标（123.13°E，30.72°N）、黄泽洋船标（122.53°E，30.5°N）、口外浮标（122.81°E，30.99°N）和南漕船标（122.52°E，30.98°N）。上海沿海的水深和浮标位置见图1。观测资料时间段为2011年1月1日—2015年11月20日，时间间隔为1 h；

（2）上海台风研究所WAVEWATCH III（WW3）海浪模式预报有效波高。数据时间段为2014年9月24日—2015年11月20日。模式的区域为5°—45°N，105°—145°E，空间分辨率为0.1°×0.1°，空间每点离散化波浪谱的方向分辨率为15°，即24个方向；时间分辨率为6 h，每天进行两次预报，分别为08时和20时（北京时，下同），预报时效168 h；所用风场是来自美国国家环境预报中心（National Centers for Environmental Prediction，NCEP）的AVN（Aviation）全球大气环流业务模式的分析场和预报场，在输入模式前还对模式风场的系统性误差做了订正，以提高预报质量。在计算站点预报时，使用双线性插值方法将格点预报插值到站点。

2.2 回归分析方法

设y为最大波高，x为有效波高，x、y的关系由一元n次回归方程确定，即：

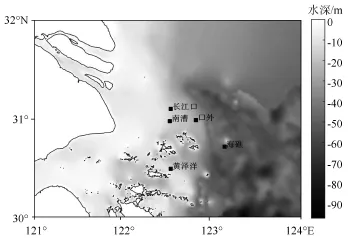
图1 上海沿海水深及浮标位置分布图

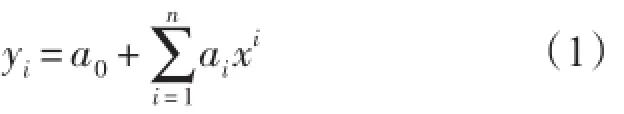
为了分析不同回归方程的效果，本文分别建立了x和y的一元一次和一元二次回归方程。

2.3 检验统计量

本文使用的检验统计参数包括：相关系数、平均误差、平均绝对误差、最大绝对误差和均方根误差。

（1）相关系数：

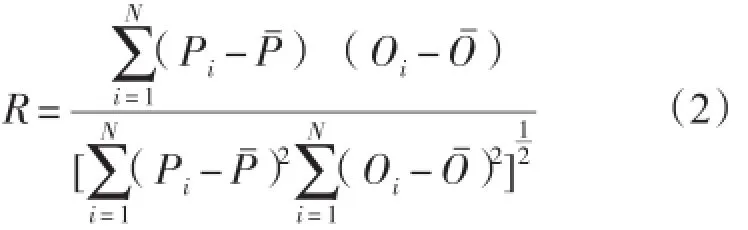
式（2）—（6）中：Pi为预报值，Pˉ为预报平均值，Oi为观测值，Oˉ为观测平均值，N为样本个数。

3 回归方程的建立和试报分析

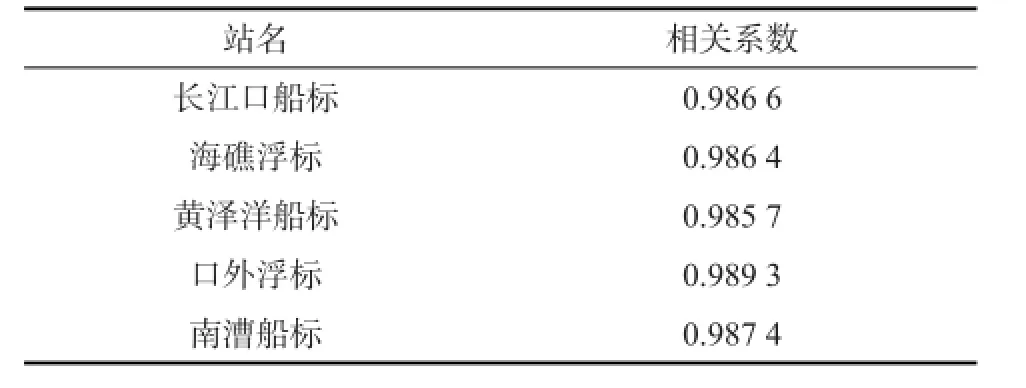
表1 各站x和y的相关系数

3.1 单站回归方程建立

各单站资料实测有效波高x和最大波高y的相关系数见表1。从表1中可以看到，5个站点的最大波高和有效波高的相关系数均在0.98以上，通过了信度0.01的相关性检验（t0.01=0.24），这说明两种波高具有明显的线性相关性。

以海礁浮标为例，对2011年1月1日—2013年12月31日的有效波高和最大波高观测资料进行回归分析，得到一元一次和一元二次回归方程为：

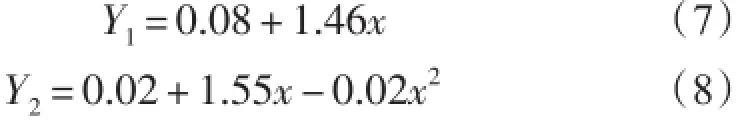
这与文圣常等[8]的理论结果接近。利用回归方程对海礁浮标2014年资料进行试报检验，结果见表2，表中正偏差代表预报值比观测值大，负偏差代表预报值比观测值小。

从表2中可以看到，对海礁浮标，建立的一元一次和一元二次回归方程得到的最大波高与实测最大波高的相关系数都为0.988 0，通过了信度0.01的相关性检验，平均绝对误差为0.1 m，说明两个回归方程的拟合效果都非常理想，同时，也有一些预报偏差较大的情况，最大绝对误差为2.0 m。此外，两个回归方程拟合最大波高的正偏差样本都多于负偏差样本，说明预报偏大的情况更多。在实际业务工作中，仅使用一元一次回归方程就可以取得比较好的预报效果。其他4个浮标站的一元一次回归方程分别为：

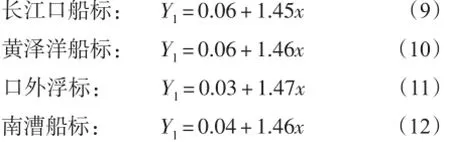
它们的拟合最大波高与实测最大波高的相关系数分别为0.986 6、0.985 7、0.989 3和0.987 4。对这4个浮标站，一元一次回归方程也很好地反映了最大波高和有效波高的关系。

3.2 通用回归方程建立

利用口外浮标、海礁浮标、黄泽洋船标、南漕船标4个站2011—2013年的有效波高和最大波高资料建立上海沿海最大波高的通用一元一次回归方程，结果如下：

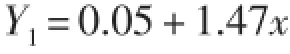
利用建立的最大波高通用回归方程对长江口船标站进行试报，检验结果见表3。

可以看到，利用4个站建立的通用一元一次回归方程，其系数a0和a1与单站一元一次回归方程的系数数值十分接近。对长江口船标进行试报，结果表明，利用通用回归方程拟合的最大波高与实测最大波高相关系数为0.988 2，通过了信度0.01的相关性检验，平均绝对误差为0.1 m。这说明，在实际预报业务中，对上海沿海最大波高进行估计时，使用通用回归方程即可达到较好的效果。

表2 海礁浮标实测最大波高y和回归分析最大波高Y的有关统计量（样本数N=7 595）

表3 最大波高通用一元一次回归方程对长江口船标资料的试报检验结果

4 数值模式预报应用

通过以上的分析，已经得到估计最大波高的客观方程，在实际业务中，只需要使用数值预报的有效波高即可进行最大波高的预报。数值模式预报与观测相比，会存在误差，在使用数值预报的结果前，需要进行检验。利用5个浮标站2014年9月24日—2015年11月20日的观测数据对WW3海浪模式的24 h有效波高预报进行检验，结果见表4。

从表4中可以看到，WW3海浪模式对5个浮标站的有效波高预报都比较准确，相关系数为0.788 6—0.915 4，均通过了信度0.01的相关性检验。平均误差最小为-0.04 m，最大也仅为-0.12 m，而平均绝对误差数值也较小，为0.2—0.3 m。从表4中也可以看到，除黄泽洋船标外，其他4个浮标站的预报以正偏差为主，这可能与黄泽洋船标附近岛屿较多、地形更复杂有关。此外，有4个浮标站的预报以正偏差为主，而5个浮标站的平均误差均为负值，说明平均而言，尽管正偏差样本占多数，负偏差的绝对值仍要大于正偏差的绝对值。

从表5中可以看到，利用WW3模式的有效波高进行最大波高预报，预报最大波高与实测最大波高具有较好的相关性，相关系数在0.778 2—0.911 2，均通过了信度0.01的相关性检验。平均误差最大为-0.17 m，最小为-0.05 m。5个浮标站平均绝对误差都为0.4 m，对于一些较大的最大波高值，预报结果偏差较大，最大绝对误差出现在海礁浮标，为3.3 m。与有效波高的预报结果一致，除黄泽洋船标外，其他4个浮标站的预报以正偏差为主。此外，平均而言，最大波高预报的负偏差的绝对值也要大于正偏差的绝对值。

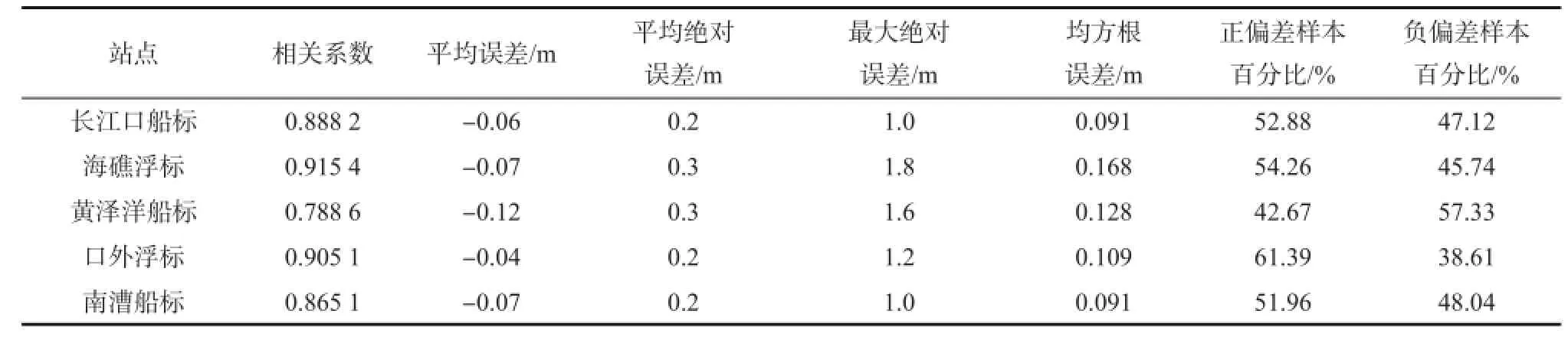
表4 WW3模式24 h有效波高预报检验

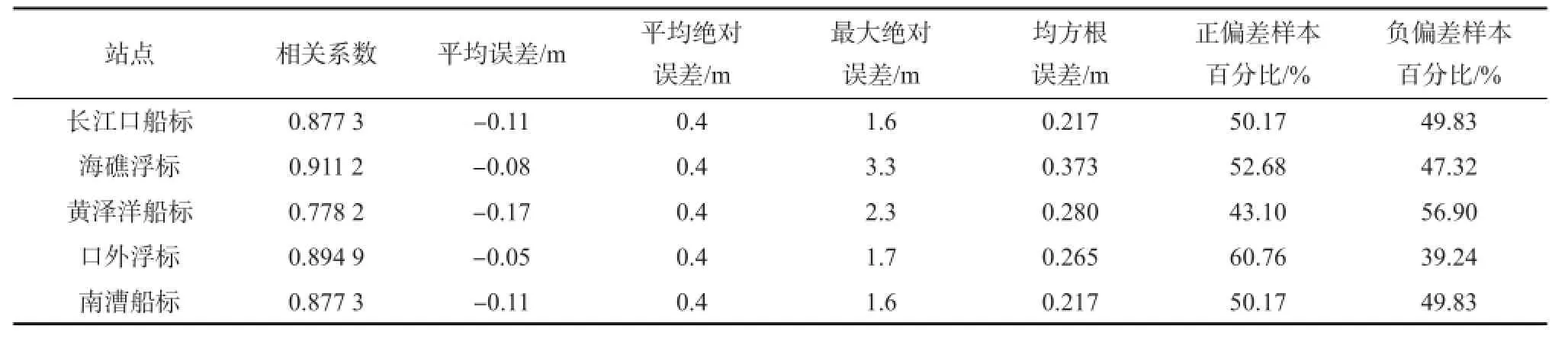
表5 实测最大波高与预报最大波高误差分析

5 结论

通过对上海沿海有效波高和最大波高关系进行统计分析，并利用WW3海浪模式进行试报，本文主要得出以下几点结论：

（1）对海礁浮标，建立的一元一次和一元二次回归方程拟合的最大波高与实测最大波高非常接近，平均绝对误差为0.1 m，两个回归方程的拟合效果都非常理想。在实际业务工作中，仅使用一元一次回归方程就可以取得比较好的预报效果。对其他4个浮标站，一元一次回归方程也很好地反映了最大波高和有效波高的关系；

（2）利用口外浮标、海礁浮标、黄泽洋船标、南漕船标4个站建立的通用一元一次回归方程，其系数与单站一元一次回归方程的系数数值十分接近。利用通用方程对长江口船标进行试报，拟合的最大波高与实测最大波高相关系数为0.988 2，平均绝对误差为0.1 m。在实际预报业务中，对上海沿海最大波高进行估计时，使用通用回归方程即可达到较好的效果；

（3）WW3海浪模式对5个浮标站的有效波高预报都比较准确，利用WW3海浪模式的有效波高进行最大波高预报，预报最大波高与实测最大波高具有较好的相关性，平均误差最大为-0.17 m，最小为-0.05 m，平均绝对误差都为0.4 m，预报效果较好。

[1]郑崇伟,游小宝,潘静,等.钓鱼岛、黄岩岛海域风能及波浪能开发环境分析[J].海洋预报,2014,31(1):49-57.

[2]郑崇伟,李崇银.中国南海岛礁建设:重点岛礁的风候、波候特征分析[J].中国海洋大学学报(自然科学版),2015,45(9):1-6.

[3]郑崇伟,李崇银.中国南海岛礁建设:风力发电、海浪发电[J].中国海洋大学学报(自然科学版),2015,46(9):7-14.

[4]闻斌,刘俊.海浪数值模式研究回顾与进展[J].海洋预报,2006, 23(4):76-81.

[5]郑沛楠,宋军,张芳苒,等.常用海洋数值模式简介[J].海洋预报, 2008,25(4):108-120.

[6]李本霞,吴淑萍,邢闯,等.近海近岸高精度海浪业务化数值预报系统[J].海洋预报,2010,27(5):1-6.

[7]孙明华.一个集合海浪预报系统及其初步试验[J].应用气象学报,2011,22(6):673-680.

[8]文圣常,宇宙文.海浪理论和计算原理[M].北京:科学出版社, 1985:177-184.

[9]刁学贤.青岛近岸波高的统计分析[J].海洋通报,1998,17(4): 19-28.

[10]李合.北部湾海区有效波高与最大波高的关系及最大设计波高[J].海洋预报,1989,6(1):46-49.

[11]Goda Y.A new Method of Wave Pressure Calculation for the Design of Composite Breakwater[R].PARI Report 012-03-02, 1973.

[12]Kim D H,Kim T.Probabilistic Distribution of the Maximum Wave Height[J].China Ocean Engineering,2014,28(5):579-586.

[13]候瑞科.利用正态分布计算年最大波高[J].海洋预报,1991,8 (2):70-75.

[14]尉华,沈正.海浪日最大波高序列的一种标度性质[J].海洋湖沼通报,1994(4):1-8.

[15]曹兵,徐常三,高清清,等.连云港海域极值波高统计分析方法研究[J].海洋通报,2014,33(1):27-35.

Analysis of the relationship between significant wave height and maximum wave height in Shanghai coastal area

ZHU Zhi-hui，SHEN Qi-yan,CHANG Ya-Nan
（Shanghai Marine Meteorological Center,Shanghai 201306 China）

Using linear regression method,the relationship between significant wave height and maximum wave height in Shanghai costal area is analyzed based on five buoys data.It is found that the two kinds of wave height has a good linear relationship.Through the establishment of regression equation of the two kinds of wave,the objective method of estimating maximum wave height is obtained.For the 5 buoys,the one-dimensional linear regression equation can well reflect the relationship between significant wave height and maximum wave height. The general forecasting equation of maximum wave height has a good performance for Changjiangkou buoy and the average absolute error is only 0.1m.The forecasted significant wave height byWW3 wave model is close to the observation.Using the significant wave height from this model to forecast maximum wave height,the forecast value has a good correlation with the observation.The averaged error at the five buoys is-0.17m,the minimum is-0.05m,the averaged absolute error is 0.4m,and the result is reasonable.

significant wave height;maximum wave height;regression analysis

P731.22

：A

：1003-0239（2016）06-0069-05

10.11737/j.issn.1003-0239.2016.06.008

2016-03-28

上海市气象局面上项目（MS201409，MS201603）。

朱智慧（1984-），男，高级工程师，硕士，从事海洋气象预报工作。E-mail:zzh830830@163.com