浅谈初中数学的情境式概念教学
2017-01-09汤奎锋
汤奎锋
浅谈初中数学的情境式概念教学
汤奎锋
数学概念的产生主要来源于现实生活和数学知识自身发展的结果,因此概念的引入通常是基于数学知识的现实原型或现实需要,或者是基于数学知识本身的逻辑结构,以旧引新。基于“数学现实”探究、建构概念,创设生活情境、趣味情境引入,进行具体的操作活动引入,联想类比概念引入,创设矛盾冲突引入。数学概念引入阶段的实施策略:典型性、适度性、有效性。
初中数学;概念教学;创设情境;数学现实
在设计教学情境时,除了让学生亲身感知问题,更需要的是促使学生展开积极思考、从实际情境中去发现数学知识。因此,情境设计的根本目的从“引趣”走向“引思”是非常必要的。数学概念的产生主要来源于现实生活和数学知识自身发展的结果,而概念的引入通常是基于数学知识的现实原型或现实需要,或者是基于数学知识本身的逻辑结构,以旧引新。
1.基于“数学现实”探究、建构概念
教师要突出学生的“主体地位”,扮演好组织者、引导者与合作者的角色,更多地关注预设以外学生的“异想天开”,善于捕捉学生的智慧火花,鼓励学生进行合情推理,训练学生的直觉思维,通过启发性的问题帮助学生形成概念。
形成一个概念,一般经历从片面到全面、从模糊到清晰、从表象到本质的复杂思维过程。如果教师给学生充分思考的时间,学生个体对于情境或者问题会做出真实的、本能的第一反应,这种思维的结果和假设在教师引导下会逐步清晰化和理想化,最终形成概念。如果由教师代替学生快体验、快抽象出数学概念,这种不连贯的学习活动,会造成学生建构的概念缺乏完整性。
[案例1]
教师设问:观察这5个数:300000、150000、653000、953700、453780,想想你有更简单的表示方法吗?
教师抛出问题,让学生进行思考和交流后,学生提出了以下3种表示方法:
第一种:3×105、1.5×105、6.53×105、9.537×105、4.5378×105
第二种:3×105、15×104、653×103、9537×102、45378×101
第三种:0.3×106、0.15×106、0.653×106、0.9537×106、0.45378×106
教师引发学生对数学概念的思考以后,还需要用启发性、探索性、层进性的问题去引发、驱动。教师可以用“你能得到什么”“你是怎样得出来的”“你为什么要这样做”等问题引发学生顿悟,从而成功建构概念。
[案例2]
为了启发学生:同一直线上的点的描述需要考虑方向和大小,在脑海里联想到数轴又从一维的直线过渡到二维平面上的点,从而设置两条数轴(两个方向),以此形成平面直角坐标系形式化的定义,设计下列问题:
(1)若老师站在教室第三排的走廊中间(图中五角星O),先请4位同学(位于图中圆点A、B、C、D的位置)说说如何描述自己的位置相对老师的位置。

(2)再请两位同学(位于图中的圆点E、F的位置)说说如何描述自己的位置相对老师的位置。
(3)回顾之前学过的有关数轴的内容——数轴的三要素以及数轴上的每一个点都对应着一个实数值,思考并交流如何表示平面上的一个点。
教师除了预设一些递进的、有针对性的问题外,还要针对学生的回答给予及时回应,随机应变地进行启发和点拨,让学生不断地修正思考的方向,这对教师的临场反应能力有一定的要求。
2.创设生活情境引入——基于概念抽象的原型
虽然有些数学概念是高度抽象后形式化的产物,但在现实生活中仍能找到许多概念的原型。因此,教学中可以利用这些概念的生活原型来创设情境,唤起学生的兴趣,让学生借助自己的生活经历,感受、体会数学概念的产生是科学发展和生产实践等实际应用的需要。
[案例3]
在教授“平面直角坐标系”概念时,教师可以创设如下情境:
题1.当破译小高手(如下表)

(1)请破译下列密码:
A5 B5 C4 E5 B1 C2(有志者事竟成)
(2)请编制密码:
天才来自勤奋(B4D2E3C5D4C3)
题2.做影院服务生
(1)你会在电影院找到电影票上所指的位置,对号入座吗?
(2)在电影票上,“4排3号”与“3排4号”是同一个座位吗?为什么?
3.创设趣味情境引入——基于概念学习的动机
有时可以创设一些生动、有趣的材料来加强学习的刺激,“以趣引思”。在具体操作中,我们要注意趣味性材料一定要和概念的属性相联系,避免“一笑而过”的情况发生。
[案例4]
在教授“科学计数法”概念时,教师可引用以下幽默故事来吸引学生的兴趣,并寓意大数的表示需要简化表达,隐含科学计数法的必要性。
有一个傻小子跟先生学字,听先生教过“一、二、三”后,心想原来写字这样简单,就让他父亲把先生辞掉了。有一天,父亲要请一位客人吃饭,让傻小子写一份请柬。可是,傻小子过了很长时间还没有出来,父亲便去问,却见他在纸上画横杠。傻小子一见父亲,便说:“你请谁不好,偏要请‘万百千’!”
4.进行具体的操作活动引入——基于概念的感性积累
有些数学概念的引入可以通过设计一些实践活动,让学生在活动中体验、感悟概念的内涵,从而积累感性认识,为概念的形成作铺垫。例如,在“平移”的教学中,除了观察生活中的平移现象外,可以让学生尝试用几何画板软件移动电脑屏幕上的三角形。运用软件中的轨迹跟踪功能显示顶点的运动轨迹,可以让学生非常直观地观察移动的方向和移动的距离。
5.联想类比概念引入——基于数学概念间的联系
在数学概念体系中,许多概念有相似的内容和结构,以及相似的研究方法。因此,在引入新概念时,通过与相关概念进行联想类比,可以得到新概念与相关概念在认识及处理方法上的一些共通点或规律。例如,在引入分式概念时,可以和分数概念进行类比;在引入向量的运算时,可以与实数的运算作联想类比。
6.创设矛盾冲突引入——基于数学知识发展的需要
有些概念的产生源于数学自身知识结构的发展,如无理数等数学概念的引入是为了解决之前数学中的某些矛盾、某种问题或满足某种需要。可通过创设问题情境,引起认知失调,激发解决问题的动机,从而引出新概念产生的必要性。
[案例5]
在学生充分展示了如何由两个小正方形(边长均为单位1)拼成一个大正方形后,教师设问:①大正方形面积是多少?(面积是2;若设边长为a,则a2=2)②它的边长是多少?是已学过的有理数吗?为什么?③它是不是之前学过的整数或者分数?
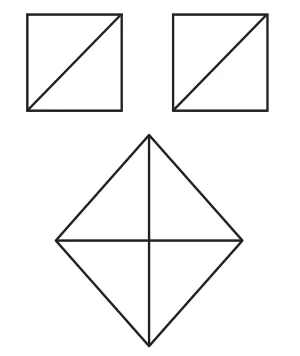
通过探讨a不是有理数,但又是客观存在的,从而引出数系从有理数扩充到无理数的必要性。
7.数学概念引入阶段的实施策略
(1)典型性。创设的情境要具有一定的典型性,蕴含数学概念的现实背景或本质属性。并不是所有的数学概念都一定要通过生活情境来引入,如果是“为了情境而情境”,往往会适得其反。
(2)适度性。在引入概念时,设计的问题或活动要符合学生的认知水平,处于学生思维的最近发展区,让学生从心理上感到亲切。其次,如果提供的感性材料数量过少,则学生的感性体验不够;如果感性材料过量又会让学生产生乏味感,因此,要把握好情境的量,让学生既能有充足的活动体验,又不会产生“情境疲劳”。
(3)有效性。好的情境才能让学生触“境”生情,激发学习的兴趣。创设的情境要避免虚假的情境,注意情境的合理性。另外,设置情境的目的不仅是感性认识的铺垫,更要让学生产生思考、发现问题。因此,在概念引入中,问题才是核心。
(编辑:胡 璐)
G633.6
A
1671-0568(2016)12-0107-02
汤奎锋,安徽省怀远县唐集中学教师。
