船舶水下电场的预测方法*

谭 浩，陈 聪，蒋治国

(海军工程大学 理学院 应用物理系， 湖北 武汉 430033)

船舶水下电场的预测方法*

谭 浩，陈 聪，蒋治国

(海军工程大学 理学院 应用物理系， 湖北 武汉 430033)

为了实现对船舶水下电场信号目标特征的控制，提出一种信号预测的方法。对测得的信号进行小波分解并分别在静电场和轴频电场频段进行重构。对高频的轴频电场信号构建自回归预测模型，对低频的静电场信号以灰色GM(1，1)模型进行拟合。将预测结果进行叠加得到对下一时刻电场信号的预测值。实测数据对该方法的检验结果表明：用该方法对船舶水下电场进行预测，电场的预测误差在原信号幅值的20%以内。

水下电场；预测模型；小波分解；灰色GM(1，1)模型；自回归模型

船舶在海水中的腐蚀过程会产生电流，为了抑制船体腐蚀，船身普遍安装有阴极保护系统。不过抑制腐蚀的过程，也伴随着防腐电流的输出，因此，船体在其海水周围会产生静电场，由于海水扰动和电器设备稳定性等因素的影响，静电场会在0.1 Hz的频率左右波动。与此同时，腐蚀与防腐电流会经海水从船壳(铁质)流向螺旋桨(铜质)，并通过轴承、密封和机械线路从螺旋桨返回到船壳形成电流回路，该回路的电阻会随着螺旋桨轴承的旋转而发生周期变化，从而使海水中的电流受到调制。这些时变电流会以转轴的转动频率为基频，以谐波的形式由船体向外传播，从而产生基频与螺旋桨转动频率一致的轴频电场(1～7 Hz)。静电场和轴频电场都是船舶水下重要的目标特征信号源[1]。

从20世纪50年代起，西方国家和苏联就非常重视船舶水下电场的研究[2]，到目前为止已经设计并投入使用了许多高性能的水下电场测量装置和抑制自身水下电场信号特征的装置[3]。相比之下，我国在该领域的研究与国外先进水平存在非常大的差距，很多工作尚处于基础研究阶段。

比较目前国内在船舶水下电场领域的各项工作，电场信号的电偶极子建模研究方面已相对成熟，理论和实验研究都显示，一定范围内一对电偶极子在水下能够等效为船舶产生的水下电场[4-5]。在此成果的基础上，对于船舶水下电场预测方法的研究就显示出了实际意义：如果能够估计出船舶的水下电场在未来时刻产生的电场值，施加一个与船舶电场等大反向的电场即可使自身船舶的电场目标特征得到控制，而剩余的水下电场值即为预测误差。因此，预测的准确程度能够反映出电场控制的效果。

本文在分析海洋实测数据的基础上，针对船舶水下电场以及海洋环境噪声的特点，提出了一种基于小波分解的灰色GM(1，1)_AR模型的船舶电场预测方法。

1 电场数据的获得及信号特性分析

通过自行研制的一套船舶电场采集系统于渤海某海域进行了一次海上实船水下电场的测量，获取数据。根据电偶极子模型，只有测量电极无限接近时，两电极测得的电位差才能近似等于电场值。实际测量中，为了增大信号的信噪比，将电极距适当增大，电场值由测得的电位差与电极距的比值计算得到。

水下电场测量系统主要由岸上控制主机和测量体两部分组成，两者之间通过水密电缆相连。岸上控制主机包括一台计算机和一个通信Modem；水下测量体则包括电极支架、深度传感器、电场传感器和置于密封桶内的信号调理电路。其中，信号调理电路对采集到的信号先差分放大100倍，经过10 Hz六阶低通滤波再放大50倍。采样率为128 Hz。

传感器采用全固态Ag/AgCl电极，测量电极之间的距离设置为3 m，平行于螺旋桨转轴放置，与转轴距离约4 m。由于测试用船的螺旋桨为变矩桨，可调整螺旋桨使其转动时不产生推力，所以本次测试在码头进行。尽管港口内环境干扰噪声相对于海上的干扰更大，但是在码头进行试验可保持电极与螺旋桨的位置相对固定，而且电极对与螺旋桨之间较近的距离也保持了测得的电场信号的信噪比相对较高，且实施操作更加方便。

为了获得更加全面的信息，在测量船舶电场数据之前首先对该海域大量的环境电场数据进行了测量，其中一组数据如图1所示。

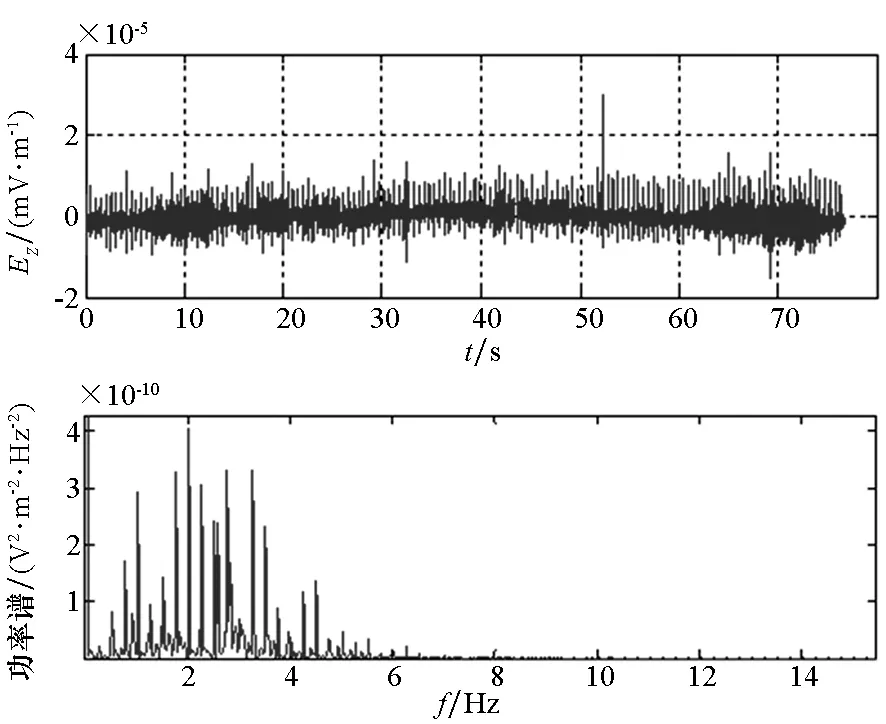
图1 环境噪声的时域和频域幅值Fig.1 Noise in time and frequency zone

由环境噪声的频谱部分可以发现，该海域的环境电场主要集中在4 Hz以下的频段(经分析主要为人为噪声，实际海洋电场噪声主要集中在1 Hz以下[1])，所以为了更好地验证本方法的有效性，提高信号的信噪比，可调节螺旋桨的转动速度到避开环境噪声较集中的频段。测得的其中一组轴频电场序列及其功率谱如图2所示。

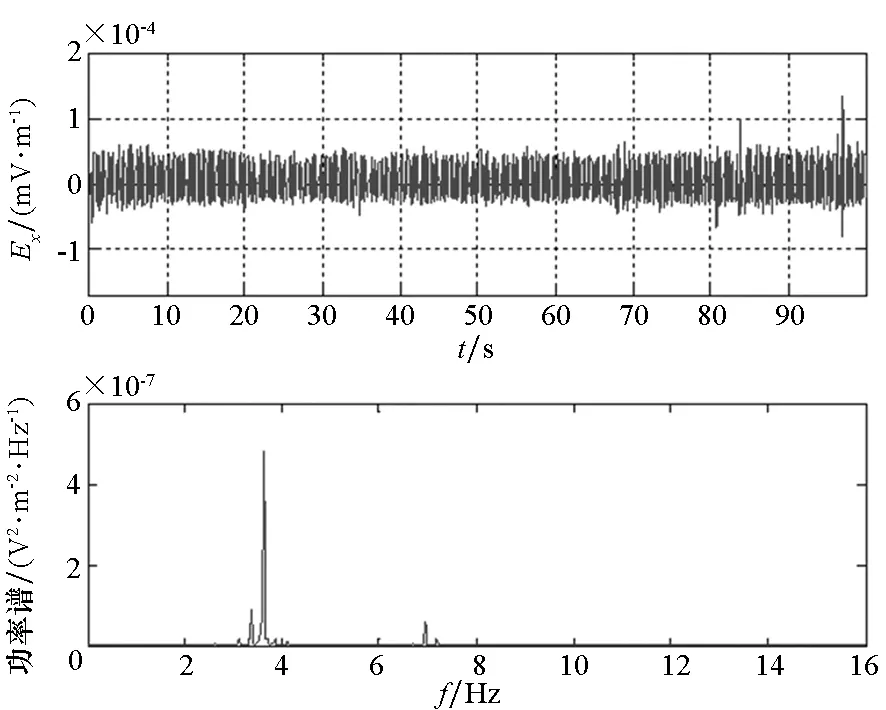
图2 实船轴频电场信号的时域值与功率谱Fig.2 Shaft-rate electric field signal in time zone and the power spectrum

较低频率的静电场主要集中在0.1 Hz左右的频段，即测得的船舶水下电场信号为带有不明显趋势的非平稳时间序列。所以，对该信号进行预测的基本思想为：把信号分为分别对应于轴频电场以及静电场的高频信号和低频信号两个部分，分别对其进行预测，之后把各自的预测结果相叠加得到对信号的预测值。

然而在传统的统计学中，各种方法和结论只有在样本趋于无穷大时其性能才有理论上的保证，而在众多的工程实际中，样本数常常是有限的，这就导致很多传统的统计分析方法难以取得理想的效果。对于均值具有趋势性的非平稳时间序列预测问题，关键取决于如何提取时间序列中的低频和高频成分并进行建模以及如何避免对高频信息的过拟合。

为了解决这类问题，考虑到二进正交小波对非平稳时间序列的适应性[6]，采取该方法对高低频成分进行分离。对于低频成分而言，灰色系统是建立系统运行趋势模型的有效方法，适用于动态预测，且只需少量已知信息就可建立预测模型；对于频谱特性明显的轴频电场的高频成分，则可选用具有线性特征的自回归(Auto Regressive, AR)预测模型进行预测。

2 信号预测的原理及方法

2.1 信号的小波分解与重构

首先将测得的水下电场数据进行小波分解，并分别在轴频段和静电场的频段进行重构。多分辨分析理论认为一个信号可以分解为低频信号和高频信号两部分。

设f0为待分解信号，由分解算法有：cj+1=Hcj，dj+1=Gdj，j=0,1,…，J。其中，H和G分别为低通滤波器和高通滤波器的传递函数；J为最大分解层数；cj+1和dj+1分别为f0在分别率2-(j+1)下的低频信号和高频信号，最终将f0分解为d1,d2,…，dJ和cJ。该分解算法利用二抽取，使得每层分解比分解前的信号数据长度减半，而总输出数据长度与输入数据长度保持一致。

经Mallat算法分解后的信号可采用重构算法进行二差值重构。设H*和G*分别为H和G的对偶算子，可采用式(1)对分解后的信号进行重构。

Cj=H*Cj+1+G*Dj+1，j=J-1，J-2，…，0

(1)

对d1,d2,…,dJ和cJ分别进行重构，得到D1,D2,…,DJ第1层至第J层的高频信号重构和CJ的第J层低频信号重构，其中Cj和Dj分别为cj和dj构成的列矩阵，分别对应于分解后的静电场与轴频电场信号。在Mallat重构算法中利用二插值，在输入数据序列的每相邻数据之间补一个零，使得数据长度增加一倍，以恢复抽取前的数据长度[7]。

2.2 灰色GM(1,1)预测模型

GM(1，1)是关于数列预测的一个变量、一阶微分的预测模型[7-8]。原始时间序列按时间累加后所形成的新的时间序列呈现的规律，可用一阶线性微分方程的解来逼近。因此，可以此模型对静电场频段的信号进行预测。

设测量到的信号为：

X0(t)={x0(1),x0(2),…,x0(n)},x0(i)>0,

i=1,2,…,n

分别令

(2)

GM(1，1)模型x0+az=b对应的白化微分方程为：

(3)

则有式(4)成立，从而可求得参数a,b的值。

[x0(2),x0(3),…,x0(n)]T

(4)

模型白化方程时间响应函数为：

(5)

对式(5)两边进行求导，得

(6)

即为未来时刻的信号预测值。

2.3 AR预测模型

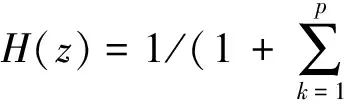
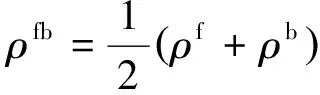
由于时间序列是各态历经过程函数的取样，因此可用时间平均代替集合平均，则有：

(7)

(8)

前、后向预测误差和反射系数在不同阶次时的递推关系为：

(9)

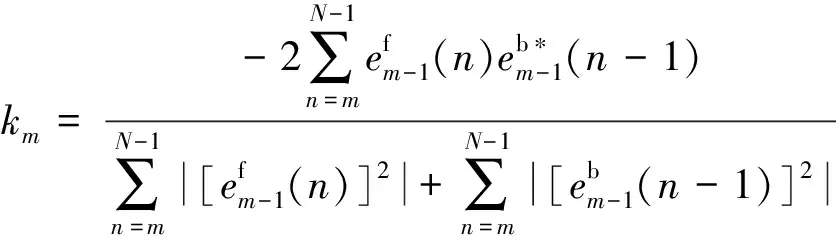
m=1,2,…,p

(10)

得到km后，在m阶时的AR模型系数仍然由Levinson算法递推求出，即有：

k=1,2,…,m-1

(11)

其中：am(k)为p阶AR模型在m阶时的第k个系数，k=1,2,…,m-1；ρm为在m阶时的前向预测误差最小功率。AR参数在第m-1阶时即可求出。

3 算例

测得的船舶电场原始数据及分解的结果如图3所示。建模样本取400点，之后均采取一步预测并做差值运算验证预测模型准确度。

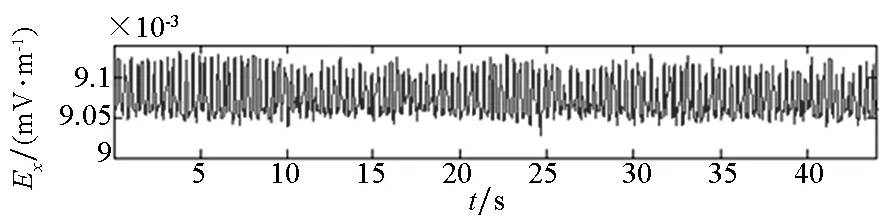
(a) 电场序列(a) Electric field sequence

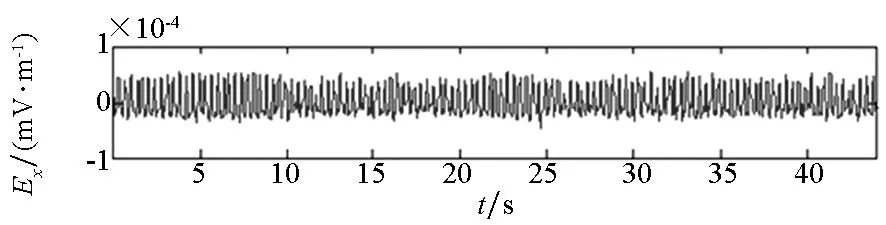
(b) 高频分量(b) High frequency components

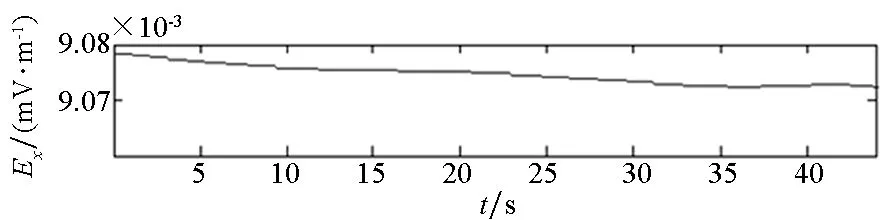
(c) 低频分量(c) Low frequency components图3 原始信号及其高、低频分量信号Fig.3 Original signal, high frequency components and low frequency components in time zone

采用基于db3小波分解、灰色GM(1，1)_AR预测模型对信号进行预测，预测效果如图4所示。以预测信号与原信号的差值的幅度谱作为评价标准。幅度谱计算方法为：在信号中截取等长度的10段序列(序列之间可以相互重叠)，分别对每段信号采用周期图法计算512点功率谱，并取平均值，再进行开方，计算结果取其10倍常用对数。预测误差的时域值如图5所示，原信号以及预测误差的幅度谱如图6所示。

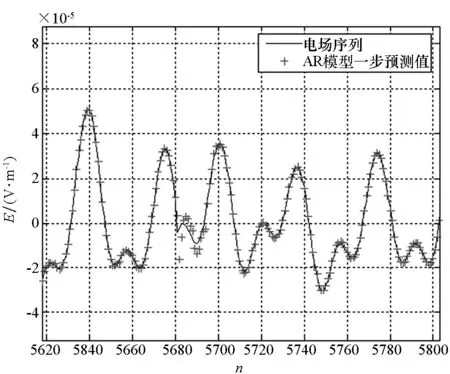
图4 实船轴频电场预测效果Fig.4 Prediction of SR electric field signal

图5 预测误差的时域值Fig.5 Error in time zone

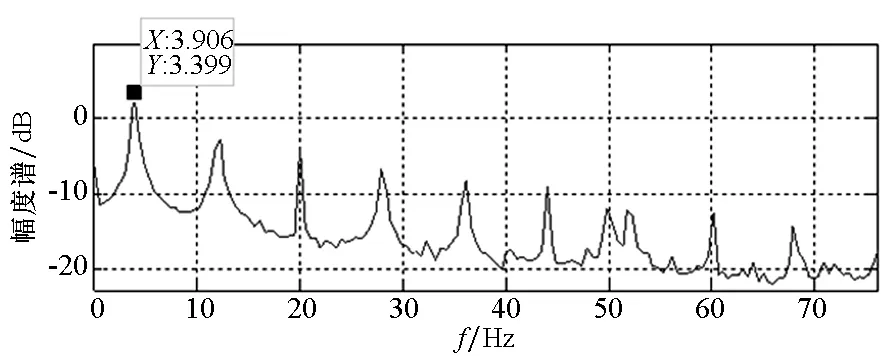
(a) 原信号的幅度谱(a) Amplitude spectrum of original signal

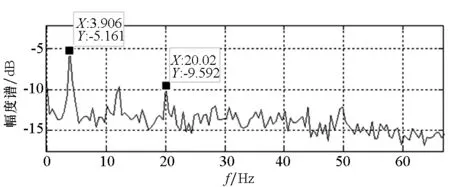
(b) 差值的幅度谱(b) Amplitude spectrum of error图6 原信号与预测误差的幅度谱Fig.6 Amplitude spectrum of original signal and error

由图6中预测误差的时域值可以发现，预测误差的时域峰值大约为原信号的30%左右。在信号的幅度谱中，3.9 Hz处原信号从3.399 dB降低到预测误差的-5.161 dB，设信号控制前后信号时域的幅度分别为A和B，则有10 lg(B/A)=-8.56，计算得到预测误差大约为原信号的13.93%。

处理后的信号中有明显的大约周期为500个数据点的“尖峰”出现，其并非由于方法的有效性存在问题，而是由于硬件系统设计时的缺陷所致。测量过程中数据存储写入SD卡所持续的时间内，采集到的数据没有存储，所以会有周期性数据点的丢失，如图5中写入时间对应于5680的点所示。丢失数据后，波形会出现不平滑的“突变”，导致预测的不准确。而实际的信号特征控制过程中不存在数据长时间存储的情况，所以不会出现类似问题。

由于以上所进行处理的仅为一组数据的结果，不具有普遍性，为验证方法的适用性，另对该海域其他时段的测量数据和实验室不同时段的共十几组测量数据进行了预测有效性检验。尽管不同数据的信噪比各不相同，这些数据的预测误差均能控制在20%以内。对比所有数据的预测误差发现，信号的信噪比越高，预测的效果越好；信号中混入噪声越多，预测模型的阶数需要得越高，模型越复杂。因此，本方法在使用中需要根据不同海域和不同时段的噪声变化调整预测模型的参数，这也是本方法的局限性所在。

4 结论

水下电场是海水中船舶产生的重要的目标特征信号之一，预测方法的研究对其信号特征控制方面具有重要意义。本文将基于小波分解理论的灰色GM(1，1)模型和AR预测模型用于船舶水下电场的预测，采用实测数据进行了计算。结果表明，该方法能对船舶电场信号进行有效的预测，误差能够维持在原信号的20%以内，能够为该领域探测和信号特征控制方法的研究提供参考。

需要注意的是，该方法对船舶水下电场的预测在近场条件下的使用会受到限制，因为静电场的场源是整个船体受到腐蚀的区域，不同于轴频电场明确在螺旋桨附近，因此近场条件下的静电场无法等效为单个的电偶极子。如何对近场条件下船舶水下静电场进行建模，进而实现对其信号的预测和控制将是下一步研究重点。根据目前所掌握的资料，边界元方法在该领域中能够发挥重要作用，这也是下一步研究的方向。

References)

[1] 林春生， 龚沈光．船舶物理场[M].北京： 兵器工业出版社， 2007． LIN Chunsheng， GONG Shenguang. Physical field of ships[M]. Beijing: The Publishing House of Ordnance Industry， 2007.(in Chinese)

[2] 姜润翔， 史建伟， 龚沈光.船舶极低频电场信号特征分析[J]．海军工程大学学报， 2014， 26(1)： 5-8． JIANG Runxiang， SHI Jianwei， GONG Shenguang. Analysis of characteristics of ship′s extremely low frequency electrical field[J]．Journal of Naval University of Engineering， 2014， 26(1)： 5-8．(in Chinese)

[3] Jeffery I, Brooking B. A survey of new electromagnetic stealth technologies[C]//Proceedings of the ASNE 21st Century Combatant Technology Symposium, 1998.

[4] 熊露， 姜润祥， 龚沈光． 浅海中船舶轴频电场建模方法[J]. 国防科技大学学报， 2014， 36(1)： 98-103． XIONG Lu,JIANG Runxiang, GONG Shenguang. Ship modeling method of shaft-ELFE in shallow sea[J]. Journal of National University of Defense Technology, 2014, 36(1): 98-103．(in Chinese)

[5] 陈聪， 李定国， 蒋治国， 等． 二次等效法求三层媒质中静态电偶极子的场分布[J].物理学报， 2012， 61(24)： 2441011-2441017. CHEN Cong, LI Dingguo, JIANG Zhiguo, et al. Electric field of a static electric dipole in three-layer medium model[J]. Acta Physica Sinica, 2012, 61(24): 2441011-2441017. (in Chinese)

[6] 吴正国， 尹为民， 侯新国, 等． 高等数字信号处理[M]． 北京： 机械工业出版社， 2009． WU Zhengguo, YIN Weimin, HOU Xinguo, et al. Advanced digital signal processing[M]. Beijing: China Machine Press, 2009. (in Chinese)

[7] 许绍杰， 王晗中， 王年生, 等. 改进不等时距灰色GM(1,1)模型及其应用[J].数学的实践与认识, 2011, 41(8): 108-114. XU Shaojie, WANG Hanzhong, WANG Niansheng, et al. Research on amendatory unequal interval grey model[J]. Mathematics in Practice and Theory, 2011, 41(8): 108-114. (in Chinese)

[8] 邓聚龙.灰理论基础[M].武汉: 华中科技大学出版社, 2002． DENG Julong. Grey theory fundation[M]. Wuhan: Huazhong University of Science and Technology Press， 2002.(in Chinese)

[9] 胡广书． 数字信号处理: 理论、算法与实现[M]． 北京： 清华大学出版社， 2003． HU Guangshu.Digital signal processing: theory, algorithm and implementation[M]．Beijing：Tsinghua University Press，2003.(in Chinese)

Electric field prediction method for ships at sea

TAN Hao， CHEN Cong， JIANG Zhiguo

(Physics Department, College of Sciences, Naval University of Engineering, Wuhan 430033, China)

To weaken the strength of the signals, a prediction method was presented. The electric field signal was decomposed into a low frequency signal and several high frequency signals. The high frequency part was predicted with auto regressive prediction model and the low frequency part was predicted with GM(1，1) model. The prediction result was the superimposition of the respective prediction. Based on the measurement at sea, the simulation results show that the prediction error of the electric field can be controlled within 20% of the amplitude of the signal.

electric field in sea; prediction model; wavelet decomposition; gray GM(1,1) model; auto regressive model

10.11887/j.cn.201606027

2015-05-31

国家自然科学基金资助项目(51109215)

谭浩(1984—)，男，湖北武汉人，讲师，博士，E-mail：22892728@qq.com

U675.6

A

1001-2486(2016)06-168-05

http://journal.nudt.edu.cn