内埋式弹舱与弹体相互影响的精细模拟
2017-01-07张群峰闫盼盼黎军
张群峰, 闫盼盼, 黎军
(1.北京交通大学 土木工程学院, 北京 100044; 2.中国航空工业集团公司 沈阳飞机设计研究所, 辽宁 沈阳 110035)
内埋式弹舱与弹体相互影响的精细模拟
张群峰1, 闫盼盼1, 黎军2
(1.北京交通大学 土木工程学院, 北京 100044; 2.中国航空工业集团公司 沈阳飞机设计研究所, 辽宁 沈阳 110035)
为了研究内埋式武器舱弹体投放过程中下落弹体与舱体之间强烈的相互作用,利用基于Menter SSTk-ω湍流模型的分离涡模拟方法,结合六自由度刚体动力学方程和重叠网格技术对某一简化开式弹舱和弹体模型的三维流场进行了非定常计算,利用非平稳信号处理方法平滑伪Wigner-Ville分布分析了舱内测点压力的时频特性。研究结果表明:在弹体出舱过程中,剪切层被破坏,导致舱体内流动状态发生较大改变,不再呈现开式舱体自持振荡特性,舱体内噪声的各阶单调声模态不明显,受弹体的影响,舱体内强度较高的涡结构主要集中于舱体后缘,使舱体后缘噪声水平升高;弹体出舱后剪切层迅速重建,自持振荡回路再次形成,舱体流动状态恢复为典型的纯空舱流动状态,但受弹体头部加速气流的影响,剪切层不稳定性增强,导致舱体内部噪声水平升高。弹体在出舱过程中由于剪切层影响受到抬头力矩的作用,使得弹体具有较大的迎角。弹体出舱后,在迎角的影响下,弹体开始受竖直向上的力和低头力矩的作用,竖直向上的力会阻碍弹体的下落。同时,弹体下落过程受舱体强非定常流场的影响,弹体受力也存在强烈的波动。研究结果为内埋武器舱优化设计和制定武器安全投放控制规律提供参考。
流体力学; 内埋舱; 武器分离; 重叠网格; SST分离涡模拟; 平滑伪Wigner-Ville分布
0 引言
武器装载于内埋舱有助于战斗机降低阻力和减小雷达探测面积,其逐渐替代外挂式而被广泛采用。然而当舱门开启时,开式流动内埋式武器舱内部存在极其复杂的流动物理现象,弹舱内会形成大幅度的压力脉动,造成剧烈震荡并产生刺耳的噪声,对控制武器的电子系统及相关结构造成疲劳破坏[1]。
为了研究内埋式弹舱的复杂流场,研究人员通常把弹舱简化为矩形空腔来研究流场的稳态和动态特性,并已经进行了大量的试验及数值模拟研究,研究表明:腔体的长深比[2-3]、腔体形状[4]、来流马赫数[5]、来流边界层厚度[6-7]及有无控制措施[8]等因素均会对腔体内噪声环境产生影响。基于简化纯空腔流动的研究结果,文献[9-10]分别对舱体带弹和弹体固定在舱体不同位置时的流场进行了研究,给出了弹体固定时舱体流场特性。值得提出的是,飞机在进行武器投放时,弹体下落过程中,弹舱剪切层存在破坏和重建过程。这种强烈的相互作用一方面使得空舱具有更强的非定常流动特性;另一方面,在弹体穿越剪切层的过程中,受舱体内强非定常流场及剪切层的影响,弹体受力出现较大幅度的波动,弹体的下落姿态也发生较大的变化,这一阶段很大程度上决定了整个发射过程的成败。为了保护舱内的机载设备和投放安全,同时保证弹体分离品质,对弹体投放过程内埋式舱体与弹体间相互影响进行深入研究显得尤为重要。
现阶段采用风洞试验技术研究内埋投放主要有可控轨迹试验(CTS)和风洞自由飞试验两种,其中CTS基于准定常假设,对于强耦合条件下的分离问题预测,无法获得强非定常非线性效应。自由飞技术可以克服上述问题,但是难以精确控制投放分离的初始条件,同时无法获得瞬态流场的精细化流动结构。由此可见,由于受试验设备和试验安全的限制,采用试验手段研究弹体投放过程中弹体和弹舱的强耦合流动特性具有一定的局限性。而数值模拟方法则有其优越性,尤其是一些新型湍流模拟方法的出现,使得计算精度有较大幅度的提高。本文将通过求解三维非定常Navier-Stokes方程,采用基于SSTk-ω模型的SST-IDDES方法,并利用重叠网格技术[11-12]和求解刚体动力学方程实现弹体的运动,研究舱门打开后到弹体发射完成整个过程中,弹体与弹舱之间强烈的相互作用。
1 数值计算方法
内埋式舱体和弹体的内外流场控制方程包括连续方程、动量方程、能量方程、气体状态方程、湍流模型方程和几何守恒方程(SCL)[13-14]。限于篇幅,这里仅介绍本研究中所用到的SSTk-ω模型和SST DES模型、控制方程的离散方法、重叠网格法及计算方法验证。
1.1 Menter SST k-ω模型
剪应力修正的SSTk-ω模型混合了k-ω模型和k-ε模型的优势,在近壁面处使用k-ω模型,而在边界层外部区域采用k-ε模型。SSTk-ω模型包含了修正的湍流黏性公式,考虑了湍流剪切应力的效应,能更精确地模拟逆压梯度引起的分离和分离区大小,SSTk-ω模型公式[15-19]为

(1)
(2)
式中:ρ为密度;k为湍动能;t为时间;U为速度向量;Ug为网格移动速度,可以通过SCL方程进行求解得到;μ为分子黏性系数;μt为湍流黏性系数

(3)

(4)
Pk为湍动能生成项;ω为湍流耗散比,β=0.075;α=α1F1+α2(1-F1),α1=5/9,α2=0.44;σk1=0.85;σω1=0.85;S为应变率张量;

(5)
y为网格格心到最近壁面的距离,ν为运动黏度,

(6)
Pk=min(μtS2,10Cμρkω);
(7)
Cμ=0.09;σω2=0.856.
1.2 SST DES模型
Spalart将大涡模拟(LES)方法和一方程 (S-A)湍流模型相结合,用S-A湍流模型和LES方法分别模拟以耗散和大涡输运为主要流动特征的区域,并通过当地网格尺度与壁面距离的比较和判断,实现这两种模拟方法的自动转换,构建了分离涡模拟(DES)方法,被习惯性称为DES97[20-21]。由于网格分布不当时,会产生因雷诺应力不匹配而形成的模化应力损耗,甚至出现非物理的分离。为了解决这一问题,2006年,Spalart等通过对边界层参数进行控制,延迟了RANS湍流模型的作用,提出了Delayed-DES(DDES)模型[22]。
2008年Shur等[23]通过引入壁面模化大涡模拟(WMLES)成功克服了对数律不匹配问题,并重新定义亚格子长度尺度为
ΔIDDES=min{max[cwdw,cwhmax,hwn],hmax},
(8)
提出了Improved-DDES。式中:hwn是垂直壁面方向的网格步长;dw为到壁面距离;cw为经验常数,取0.15;hmax为hwn的最大值。Strelets[24]提出以SST模型代替S-A模型的SST-DES模型,使得新的混合模型兼有了SST模型的诸多优点。2012年Gritskevich[25]对SST DDES和IDDES模型的常数进行了进一步的精确校准,下述文中的SST DES均指的是SST-IDDES模型。
1.3 平滑伪Wigner-Ville分布时频分析法
无论是弹体投放中弹体出舱穿越剪切层还是弹体出舱后头部加速区与剪切层相互干扰,都会使得弹舱内部压力脉动发生较大变化而改变舱体声学特性。由于弹体下落的影响,舱体内部脉动压力数据属于非平稳信号,因此不能采用传统傅里叶变换来处理弹体下落过程中舱内的压力脉动,此时必须采用时频分析技术进行舱内监测点压力脉动的频谱特性分析。
对于非平稳信号,现在已有许多时频分析技术,如短时傅里叶变换(STFT)、小波变换(WT)、Wigner-Ville分布(WVD)及平滑伪Wigner-Ville分布(SPWVD)。STFT方法存在时间分辨率和频率分辨率的矛盾,导致时频聚集性很差。WT时频聚集性比STFT优异,但是计算复杂耗时很长,不利于较大数据量的计算。WVD属于二次型时频描述法,由于二次型时频方法固有特性,严重的交叉干扰对其应用范围有较大限制。SPWVD方法继承了WVD的优点同时对交叉干扰进行了平滑处理,因此在计算量和精度上都是适当的。本文即选用SPWVD方法对弹体下落过程中舱体内部压力非平稳信号进行时频分析,以得到舱体声学特性变化。信号x(t)的SPWVD定义[26]为
SPWVDx(t,f)=

(9)
式中:g(u)h(τ)为实对称窗函数,其长度可以独立进行选择。
1.4 重叠网格和离散格式
重叠网格法中存在两套或多套相互交叠的网格,分别称为背景网格区域和重叠网格区域。在计算中通过将背景网格中被重叠区遮挡的网格隐藏,通常称之为“挖洞”,形成一套计算网格。如果重叠网格区域发生移动,则按一定规律重新进行“挖洞”,来得到新的计算网格,即可实现重叠网格区域的运动。背景网格与重叠网格相交的边界区域通过一定的方法进行插值来实现变量值的传递,并保证数值解在交界处光滑过渡。
控制方程对流项的空间离散采用具有2阶精度的Roe格式,扩散项采用中心差分格式。选取修正的Venkatakrishnan[27]限制器保证2阶精度插值且具有TVD性质,同时又具有较小的数值耗散。非定常计算的时间离散涉及控制方程中每一个与Δt有关的项。物理量φ随时间变化描述为
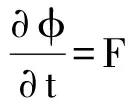
F(φ)包含所有的空间离散项。计算中引入双重时间步法,即在控制方程中引入虚拟时间项,利用物理时间步求解真实解,而每一物理时间步通过虚拟时间迭代达到收敛。
1.5 数值方法验证
1.5.1 对空腔噪声计算方法的验证
开式流动腔体会在腔体唇口处形成剪切层,剪切层由于自身不稳定性或外界扰动形成脱落涡,脱落涡向后传播并与腔后壁碰撞,产生强烈的噪声形成声波,声波通过空腔内部向上游传递,与腔体前壁相撞后激发了剪切层内新的涡生成、发展与脱落,再次与后壁相撞,形成二次声波,在满足一定的空气动力条件和相位条件时,腔内流动形成自激振荡。自激振荡产生后会形成声波反馈回路,诱发腔内产生强烈噪声,出现多个声压级峰值的激振频率。
为了研究空腔气动声学特性,欧洲QinetiQ组织对M219空腔进行了多轮风洞试验得到了可信的试验数据。M219腔体为典型开式空腔[28],尺寸:长L为0.508 m,宽W和深D均为0.101 6 m,长深比L/D=5∶1. 模型几何尺寸如图1所示。

图1 M219模型几何形状及监测点分布Fig.1 Sketch of M219 cavity anddistribution of monitoring points
模型的计算网格数为1 300万,腔体内网格尺寸为1 mm,第一层边界层网格取2×10-3mm,以保证y+值在1左右。来流马赫数Ma=0.85,来流静温T=266.53 K,来流静压p=63 000 Pa. 与试验相同,在腔体底面等间距的布置了10个压力监测点。计算时间步选取1×10-5s,总的计算步为20 000步,总采样时长为0.2 s. 对空腔流动,可用Rossiter[29]、Heller等[30-31]改进的Rossiter半经验公式来估算各阶振荡频率:
(10)
式中:m=1,2,3,…;r、k为常数分别取0.25、0.57;Ma∞为远方来流马赫数;U∞为远方来流速度。由(10)式求得的各阶频率为148 Hz、363 Hz、578 Hz.
对得到的压力时域分布曲线进行傅里叶变换,得到各测点的声压级频谱图,如图2所示。从图2中可以看出求得的声压级频谱曲线与试验测得的结果及公式计算得到的结果三者吻合得很好,证明本文所采用的数值方法和网格分布可以较为准确地求解空腔噪声问题。

图2 腔底声压级分布Fig.2 SPL along the center line of cavity bottom
利用SPWVD时频分析技术对验证算例中计算结果进行时频分析。取后缘监测点10的压力时域曲线进行处理,得到其能量密度时频分布如图3所示。图3中颜色条即表示能量密度SPWVDx(t,f),其单位是Pa2/(s·Hz),较高的能量密度意味着较强的噪声水平。由图3可知能量密度主要集中分布在3个频率附近,分别对应着M219腔体的1~3阶模态,其中1阶模态能量密度较弱,2阶、3阶模态能量密度较强,说明腔体内噪声以2阶、3阶模态为主导,1阶模态噪声水平较弱,这与验证算例得到的声压级频谱图相一致。同时可以看出各阶模态的能量密度随着时间增加并不保持为常数:在0~0.04 s时间内能量密度主要分布在1阶、2阶模态,而0.04 s之后,1阶、2阶模态能量密度减弱,转为集中在第3阶模态。在0.14 s,2阶模态能量密度又有所增加、3阶模态能量密度有所减弱。这一现象即文献[32]中所提到的腔体噪声主导模态随时间的转换。通过以上分析可以看出,腔体内的压力脉动信号严格意义上是非平稳信号,因此通常采用的傅里叶变换是一种近似处理,而SPWVD方法可以精确地分析腔体内气动声学时频特性。

图3 M219腔体底部能量密度时频分布图Fig.3 Time-frequency distribution of energy density on the bottom of M219 cavity
1.5.2 弹体投放问题的验证
机翼/挂架/带舵外挂物(WPFS)模型是美国发起的第一次分离投放计算流体力学计算验证时使用的试验模型,CTS试验测试由阿诺德工程发展中心(AEDC)完成,具体的几何尺寸及结果数据详见参考文献[33]。本文以该模型试验来验证采用本文所选用数值方法并应用重叠网格技术和刚体动力学方程模拟弹体投放过程的准确性。
WPFS模型几何外形如图4所示,模型网格划分为两个区域,包含机翼及挂架的背景网格区域和包含弹体的重叠网格区域。背景网格和重叠网格区域交界处网格尺寸之比保持在1.0~1.2,以保证插值的精度。背景网格区域网格总数为1 150万,重叠网格区域网格总数为320万。壁面第一层网格尺度为2×10-3mm. 计算时间步取1×10-3s.

图4 WPFS模型几何外形Fig.4 Wing-pylon-store geometry
弹体发射时受到两个弹射力的作用,大小分别为10 679.4 N和42 717.5 N,弹射力作用距离为0.1 m,作用时间约为0.05 s,详细参数见表1. 总的计算时间为0.3 s.

表1 弹体参数及发射条件Tab.1 Missile parameters and launching conditions
图5为3个方向弹体质心位移随时间变化曲线。从图5中可以看出,计算得到的弹体位移变化与试验符合较好,由于弹射力作用,弹体下落方向位移要远大于另外两个方向的位移。图6为弹体滚转、偏航、俯仰姿态角随时间变化曲线,同样由于弹体弹射力作用,在下落初期,弹体俯仰角度增长最快,但撤去弹射力后,在重力和气动力共同作用下俯仰角又开始减小,其余两个方向姿态角保持持续增加的趋势。可以看出本文采取的数值方法可以准确地模拟弹体下落运动。

图5 弹体质心位移随时间变化Fig.5 Displacement of missile Cg versus time

图6 弹体姿态角随时间变化Fig.6 Missile attitude angle versus time
2 计算模型和网格划分
2.1 计算模型
为了更接近真实地模拟内埋舱弹体投放过程,本文选取的舱体计算模型为等比放大的M219腔体模型。舱体尺寸为4.57 m×0.914 m× 0.914 m,弹舱长深比保持5∶1. 弹体模型即为WPFS中弹体,其长度为3.38 m,弹径0.508 m,质心位于距弹头1.42 m处,弹体质量为907.2 kg,x、y、z轴3个方向的转动惯量分别为27 kg·m2、488 kg·m2、488 kg·m2.
选择的坐标系为x轴为逆航向,z轴向上,y轴向右,则按此坐标系定义,弹射力为负,弹体抬头为正、左偏航为正。
2.2 计算条件
来流马赫数Ma=0.85,静压p=6.3×104Pa,静温T=266.5 K,基于每米的雷诺数Re=1.35×107. 来流迎角为α=0°,入口条件设置为远场自由来流条件,舱体壁面均采用无滑移壁面条件。弹体投放采用弹射投放方式,弹体所受的弹射力作用规律与WPFS中弹射力作用规律一致,详见表1.
2.3 舱体网格尺寸选择
为了能准确地模拟大尺寸舱体内噪声问题,需要适当的数值方法和恰当的网格密度。对于本文所采用的数值方法已经得到了验证,但是对于大尺寸舱体内网格尺度的选择,还需进一步确定。本文将通过试算的方式来确定恰当的网格尺度。在1.5.1节已经看到,通过Rossiter公式可以准确地预测舱体的各阶模态频率,因此本文将以Rossiter公式求得的频率作为依据来检验网格尺寸是否满足要求,根据Rossiter公式求得各阶模态的频率分别为16 Hz、40 Hz、64 Hz. 本文分别选取了舱体内4种网格尺寸,分别为16 mm、12 mm、8 mm和6 mm. 壁面第一层网格尺度保持与验证算例相一致。最终4种情况总网格数目分别为350万、700万、2 400万和4 200万。
计算时间步长为5×10-5s,总计算步为20 000步,总物理时间为1 s. 计算中按照相同的方式在舱体底面均匀布置10个压力监测点,来流条件保持与验证算例相同。取监测点10将得到的结果进行傅里叶变换,得到声压级频谱如图7所示。

图7 不同网格密度下舱底声压级分布Fig.7 SPLs along the center line of cavity bottom at different mesh density
通过图7中的对比可以看出,当网格尺度从16 mm,减小到6 mm的过程中,计算得到的声压级均与理论公式求得的声压级基本相符。然而对于低频区域的宽频噪声,16 mm和12 mm网格得到的宽频噪声偏大,8 mm与6 mm网格的宽频噪声结果较小且相差不大。综合考虑计算精度、计算资源和计算时间,选取 8 mm的网格作为基准网格尺度。本文后续舱体网格划分及计算时间步长选取均采用本小节选取的尺度。
弹体网格划分时保证交界处重叠网格尺寸与背景网格尺寸之比小于1.2. 弹体壁面第一层网格厚度同样保持为2×10-3mm,总网格数目为450万。
3 结果分析
3.1 弹体投放对舱体声学特性影响
弹体下落算例中,在建立起流场之后,又对舱体带弹状态进行了0.3 s的非定常计算,之后弹体开始下落,下落时长为0.45 s,总计算时间为0.75 s. 取舱体内部前缘监测点2和后缘监测点8的压力数据进行SPWVD时频分析,得到能量密度时频分布图,如图8所示。

图8 舱体底部监测点能量密度时频分布图Fig.8 Energy density distributions on the bottom of cavity
通过能量密度时频分布图可以看出,在弹体下落之前的0.3 s内,能量密度集中在各阶模态对应的3个频率附近,由于舱体带弹的影响,频率值与Rossiter公式求得的3个模态的频率16 Hz、40 Hz、64 Hz有小幅偏差。
在0.3~0.6 s这一阶段,整个舱体内气动声学特性完全改变,从前后缘两个测点都可以看出,能量密度不再分布于各阶模态对应的频率上,而是集中于低频区域,后缘监测点的能量密度幅值较弹体下落之前存在着大幅度的增加,前缘点能量密度幅值虽然有所增加但幅度较小。这说明由于弹体的下落,舱体内噪声水平有所增高,后缘点噪声增加幅度更大,噪声环境更恶劣。通过图9的截面马赫数分布云图可以看出,这段时间为弹体穿越舱体唇口剪切层出舱过程,在此阶段舱体剪切层被破坏,开式空舱自持振荡的回路被阻断。因此舱体内气动声学特性发生显著改变,不再呈现典型的开式舱体气动特性。同时由于弹体对剪切层的干扰以及弹体下落后舱体容积改变产生的容积效应,使得舱体内压力脉动更加剧烈,噪声强度增大。图10为舱体内部Q值等值面分布图。从图10中可以看出,由于弹体下落的影响,舱体内涡结构主要分布在舱体后缘区域,与之相比舱体前部流动较为稳定,因此与舱体后缘相比前缘噪声水平较低。弹体下落后,舱体后缘噪声水平升高,增强的噪声前传使得前缘噪声水平高于弹体下落前噪声水平。

图10 Q准则等值面分布图Fig.10 Iso-surface contribution of Q criterion
在0.60 s之后,能量密度又再次集中在3个模态对应的频率附近。但是舱体后缘点各阶频率上的能量密度较弹体下落前都有所增大。当弹体头部穿过剪切层之后,弹体完成出舱过程,舱体剪切层迅速重建,自持振荡回路再次形成,舱体流动状态恢复为典型的纯空舱流动状态。从图9(c)的马赫数分布云图中可以看出,由于弹体前缘头部的加速气流与剪切层相互作用,使得剪切层不稳定性增强,同时会使得剪切层内涡传播速度增加,脱落涡具有更大的动能与后缘撞击,导致舱体后缘压力脉动更加剧烈,因此舱体后部噪声水平升高。
3.2 舱体对弹体投放的影响
内埋弹体投放过程中存在弹体穿越剪切层过程,此时弹体受到的气动力呈现出强烈的非定常特性,对弹体的姿态产生较大的影响。
图11、图12分别为弹体竖直方向受力及速度随时间变化曲线,图13、图14、图15为弹体下落过程俯仰力矩、俯仰角速度及俯仰角随时间变化曲线。从0.30 s~0.35 s弹体受弹射力作用,此时弹体所受合力较大,具有很大的加速度,短时间内速度由0增加到-3.5 m/s,由于弹射力的作用,使得弹体在这一阶段内受抬头力矩的作用,抬头角速度迅速增加,但由于弹射力作用时间短,弹体迎角约1.6°. 0.35 s时弹射力消失,弹体在重力和气动力共同作用下下落出舱。在0.35~0.42 s时,弹体受力较平稳,向下合力维持在10 kN左右,弹体下落的加速度减小,速度增幅下降但继续保持稳定增长。图16为0.38 s舱体中心截面马赫数分布云图及弹体表面压力分布云图,图16 (a)中截面为马赫数分布,弹体表面为压力分布,图16 (b)为弹体下表面压力分布云图,图16 (c)为弹体上表面压力分布云图。图17为弹体上下表面中心线压力系数分布曲线。由图17可知:弹体此时具有一定的迎角,弹体头部所在区域流动速度较低,压力较高;弹体尾部区域更靠近剪切层,所以流动速度较高,压力较低。因此弹体此阶段受到较小抬头力矩的作用,弹体俯仰角速度小幅度增加,弹体迎角持续增大,到0.42 s时,弹体迎角达到7°左右。

图11 弹体竖直方向受力随时间变化Fig.11 Vertical force of missile versus time

图13 弹体俯仰力矩随时间变化Fig.13 Pitch moment of missile versus time

图14 弹体俯仰角速度随时间变化Fig.14 Pitch angular velocity of missile versus time

图15 弹体俯仰角随时间变化Fig.15 Pitch angle of missile versus time

图16 t=0.38 s时舱体截面马赫数及弹体表面压力分布云图Fig.16 Mach number contours of cavity section and pressure distribution of missile for t=0.38 s

图17 t=0.38 s时弹体上下表面对称线压力系数分布Fig.17 Pressure coefficients of symmetric lines on upper and lower surfaces for t=0.38 s

图18 t=0.49 s时截面马赫数及弹体表面压力分布云图Fig.18 Mach number contours of cavity section and pressure distribution of missile for t=0.49 s

图19 t=0.49 s时弹体上下表面对称线压力系数分布Fig.19 Pressure coefficient distribution of symmetric lines on upper and lower surfaces for t=0.49 s
从0.42 s起,弹体开始穿越剪切层,图18 (a)为0.49 s时舱体中心截面马赫数分布云图及弹体表面压力分布云图。图18(b)、图18(c)分别为弹体下表面和上表面压力分布云图。图19为弹体上下表面中心线压力系数分布曲线。从图18 (a)中可知,弹体头部位置剪切层受到下落弹体的阻碍,撞击在弹体下表面,一部分动能转变为压能。从图18 (b)中可以看出,弹体头部下表面受到剪切层冲击的区域局部压力显著增高。从图18(b)、图18(c)及图19中可以看出弹体上表面压力明显低于下表面。弹体头部下表面的局部高压区使得弹体俯仰力矩保持为抬头力矩,上下表面较大的压力差导致气动力合力方向为竖直向上,且随着弹体出舱过程不断增大。因此在弹体穿越剪切层阶段,弹体俯仰角速度及抬头角度持续增加,且弹体下落受到较大的阻碍,下落速度增速减缓。
随着弹体进一步下落,弹体头部穿过剪切层,作用在弹体上的抬头力矩减小;同时弹体受抬头角速度的影响,弹体迎角持续增加,0.52 s时,弹体迎角增加到14°,弹体后部下表面压力继续增加,尤其是弹翼下表面压力及高压区面积也明显增大。受此影响,最终使弹体合力矩变为低头力矩,且随着弹体的迎角增加、低头力矩持续增大。当俯仰力矩变为低头力矩后,弹体抬头角速度开始减小,但迎角持续增加。到0.53 s时向下的合力减小为0,随后变为向上的合力,弹体下落速度不增反降。
直到0.67 s之后,弹体俯仰角速度减小到0并进一步变为低头角速度,弹体迎角达到最大值后开始减小,弹体的竖直方向合力开始下降,迎角的减小也使得弹体受到的低头力矩逐渐降低。
4 结论
1) 弹体投放过程中内埋舱体与弹体存在强烈的相互作用。弹体下落出舱穿越剪切层会使舱体唇口剪切层被破坏,导致开式舱体流动状态发生改变。舱体自持振荡回路被阻断,舱内噪声不再呈现明显的各阶单调声模态。受弹体的影响,舱体内涡结构主要集中于舱体后缘,且强度较高使舱体后缘噪声水平升高。
2)弹体出舱后,舱体唇口处剪切层迅速重建,舱体恢复典型空腔流动特性。但是受弹体头部加速气流的影响,剪切层不稳定性增强,脱落涡强度增高,与舱体后壁撞击产生的噪声更大,使得舱体内部声压级水平总体上升。
3)弹体下落过程受舱体强非定常流场的影响,弹体受力及力矩均出现较大幅的波动。弹体穿越剪切层时头部受剪切层撞击产生局部高压区,使弹体产生抬头力矩导致弹体姿态角发生改变出现抬头。弹体姿态角的抬头又使弹体受力发生改变,气动力阻碍弹体下落,影响飞机与弹体安全分离。
References)
[1] 冯必鸣, 聂万胜, 车学科. 超声速条件下内埋式武器分离特性的数值分析[J]. 飞机设计, 2009, 29(4): 1-5. FENG Bi-ming, NIE Wan-sheng, CHE Xue-ke. Simulation of the store separation from a cavity at supersonic speed[J]. Aircraft Design, 2009, 29(4):1-5. (in Chinese)
[2] 杨党国, 范召林, 李建强, 等. 超声速空腔流激振荡与声学特性研究[J]. 航空动力学报, 2010, 25(7): 1567-1572. YANG Dang-guo, FAN Zhao-lin, LI Jian-qiang. Cavity flow oscillations and aeroacoustic characteristics at supersonic speeds [J]. Journal of Aerospace Power, 2010, 25(7): 1567-1572. (in Chinese)
[3] 谢露, 艾俊强, 李权, 等. 长深比对空腔流动与声学特性的影响分析[J]. 航空工程进展, 2014, 5(1): 18-24. XIE Lu, AI Jun-qiang, LI Quan, et al. Effect of length-to-depth ratio on flow and aero acoustic characteristics of cavity [J]. Advances in Aeronautical Science and Engineering, 2014, 5(1): 18-24. (in Chinese)
[4] 徐路, 桑为民, 雷熙薇. 三维内埋式弹舱流动特性及形状影响数值分析[J]. 应用力学学报, 2011, 28(1): 85-89. XU Lu, SANG Wei-min, LEI Xi-wei. Numerical analysis of flow characteristics and shape effect of three dimensional internal weapons bay [J]. Chinese Journal of Applied Mechanics, 2011, 28(1): 85-89. (in Chinese)
[5] 王一丁, 陈滨琦, 郭亮, 等. 空腔噪声非线性数值模拟[J]. 国防科技大学学报, 2015, 37(4): 151-157. WANG Yi-ding, CHEN Bin-qi, GUO Liang, et al. Nonlinear numerical simulation of cavity noise [J]. Journal of National University of Defense Technology, 2015, 37(4): 151-157. (in Chinese)
[6] 张群峰,闫盼盼,黎军.边界层厚度对腔体气动声学特性影响数值模拟[J].航空动力学报, 2016, 31(3): 717-725. ZHANG Qun-feng, YAN Pan-pan, LI Jun. Numerical simulation on influence of boundary-layer thickness to cavity aeroacoustic characteristics [J]. Journal of Aerospace Power, 2016, 31(3):717-725. (in Chinese)
[7] 杨党国,罗新福,李建强.来流边界层厚度对开式空腔气动声学特性的影响分析[J]. 空气动力学学报, 2011, 29(4): 486-490. YANG Dang-guo, LUO Xin-fu, LI Jian-qiang. Analysis of aeroacoustic characteristics in open cavities influenced by boundary-layer thickness[J]. Acta Aerodynamica Sinica, 2011, 29(4): 486-490. (in Chinese)
[8] 黎军, 李天, 张群峰. 开式流动腔体的流动机理与控制[J]. 实验流体力学,2008,22(1):80-83. LI Jun, LI Tian, ZHANG Qun-feng. The mechanism and control of open cavity flow[J].Journal of Experiments in Fluid Mechanics, 2008, 22(1): 80-83. (in Chinese)
[9] 黄长强, 国海峰, 唐上钦, 等. 超声速带弹武器舱气动特性数值研究[J]. 兵工学报,2013, 34(8): 975-980. HUANG Chang-qiang, GUO Hai-feng, TANG Shang-qin, et al. Numerical research on aerodynamic characteristics of cavity with store at supersonic speeds[J].Acta Armamentarii, 2013, 34(8): 975-980. (in Chinese)
[10] 司海青, 王同光. 数值模拟有外挂物的空腔流动[J].空气动力学学报,2007, 25(3): 404-409. SI Hai-qing, WANG Tong-guang. Numerical simulations of the cavity with a store [J]. Acta Aerodynamica Sinica,2007, 25(3):404-409. (in Chinese)
[11] 朱自强. 应用计算流体力学[M]. 北京:北京航空航天大学出版社, 1998: 173-174. ZHU Zi-qiang. The application of computational fluid dynamics [M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 1998: 173-174. (in Chinese)
[12] 阎超. 计算流体力学方法及应用[M].北京:北京航空航天大学出版社,2006: 197-217. YAN Chao. The computational fluid dynamics method and its application [M]. Beijing, Beijing University of Aeronautics and Astronautics Press, 2006: 197-217. (in Chinese)
[13] Tamura Y, Fujii K. Conservation law for moving and transformed grids[C]∥Proceedings of 6th National Symposium on Computational Fluid Dynamics. Tokyo, Japan: Japan Society of Computational Fluid Dynamics, 1993: 519-522.
[14] 刘伟. 细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究[D]. 长沙: 国防科学技术大学, 2004. LIU Wei. Nonlinear dynamics analysis for mechanism of slenderwing rock and study of numerical simulation method [D]. Changsha: National University of Defense Technology, 2004. (in Chinese)
[15] Durbin P A, Pettersson B A. Statistical theory and modeling for turbulent flows[M]. 2nd ed. New York: A John Wiley Sons Ltd, 2011.
[16] Wilcox D C. Turbulence modeling for CFD[M]. La Canada, CA: DCW Industries, 1998: 142-148.
[17] Menter F R. Two-equation eddy-viscosity turbulence modeling for engineering applications [J]. AIAA Journal, 1994, 32(8): 1598-1605.
[18] Menter F R, Kuntz M. A daptation of eddy viscosity turbulence models to unsteady separated flow behind vehicles[M]∥McCallen R, Browand F, Ross J. The aerodynamics of heavy vehicles: trucks, buses and trains. Berlin: Springer Berlin Heidelberg, 2004:339-352.
[19] Menter F R, Kuntz M, Langtry R. Ten years of industrial experience with the SST turbulence model [C]∥ Proceedings of the Fourth International Symposium on Turbulence, Heat and Mass Transfer. Danbury, CT: Begell House, 2003: 625-632.
[20] Spalart P R. Detached eddy simulation [J]. Annual Review of Fluid Mechanics, 2009, 41(1):203-229.
[21] Spalart P R, Jou W H, Strelets M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[C]∥1st AFOSR international Conference on DNS/LES. Columbus, OH: AFOSR, 1997.
[22] Spalart P R, Deck S, Shur M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195.
[23] Shur M L, Spalart P R, Strelets M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities [J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649.
[24] Strelets M. Detached eddy simulation of massively separated flows [C]∥39th AIAA Aerospace Sciences Meeting and Exhibit. Reno, NV US: AIAA, 2001.
[25] Gritskevich M. Development of DDES and IDDES formulations for thek-ωshear stress transport model [J]. Flow, Turbulence and Combustion, 2012, 88(3): 431-449.
[26] Auger F, Flandrin P. Improving the readability of time-frequency and time-scale representations by the reassignment method [J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1068-1089.
[27] Venkatakrishnan V. On the accuracy of limiters and convergence to steady state solutions[C]∥ 31st Aerospace Sciences Meeting and Exhibit. Reno, NV, US: AIAA, 1994:152-164.
[28] Henshaw M J C. M219 cavity case: verification and validation data for computational unsteady aerodynamics, RTO-TR-26[R]. London: QinetiQ, 2002.
[29] Rossiter J E. Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds [R]. Farnborough: Aeronautical Research Council, 1964.
[30] Heller H H, Holmes D G, Covert E E. Flow induced pressure oscillations in shallow cavities [J]. Journal of Sound and Vibration, 1971, 18(4):545-546.
[31] Heller H H, Bliss D B. The physical mechanism of flow-induced pressure fluctuations in cavities and concepts for their suppression [C]∥2nd AIAA Aeroacoustics Conference. Hampton,VA,US: AIAA, 1975.
[32] Zhuang N. Experimental investigation of supersonic cavity flow and their control [D]. Tallahassee, Florida, US: Florida State University, 2007.
[33] Heim E R. CFD wing/pylon/finned store mutual interference wind tunnel experiment, AEDC-TSR-91-P4 [R]. Tennessee: Arnold Engineering Development Center, 1991.
Elaborate Simulation of Interaction Effect between Internal Weapon Bay and Missile
ZHANG Qun-feng1,YAN Pan-pan1,LI Jun2
(1.School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;2.Shenyang Aircraft Design and Research Institute,Aviation Industry Corporation of China,Shenyang 110035, Liaoning, China)
To study the strong interaction effect between internal weapon bay and missile during the weapon release, the unsteady flow around a simplified weapon bay and missile model is simulated using SST k-ω improved delayed detached eddy simulation (IDDES) method, six-degrees-of-freedom rigid body dynamics equations and overset mesh method. The fluctuation of pressure in the weapon bay is analyzed using the smooth pseudo Winger-Vile distribution (SPWVD) method, and the time-frequency characteristics of pressure are obtained. The research results show that, when a missile is delivered from the weapon bay, the shear layer is destroyed to lead to the change in the flow structure, the self-sustained oscillation disappears in the weapon bay, and there is no obvious cavity tone. Stronger vortexes concentrate in the trailing edge of cavity, and thus the sound pressure level (SPL) in the trailing edge of the weapon bay increases. After the missile is delivered from the weapon bay, the shear layer is rapidly reestablished and the self-sustained oscillation shows up again. The impact of the accelerated flow near the head of the missile leads to enhance the instability in shear layer. Accordingly, the sound pressure level in the weapon bay is enhanced. The missile flies at a large angle of attack since it is affected by upward force moment during passing through the shear layer. After the missile is delivered from the weapon bay, it begins to be affected by vertical upward force and pitch down moment. The vertical upward force can hinder the missile from falling. Meanwhile, the force and moment acting on the missile fluctuate strongly under the effect of the unsteady flow in the weapon bay.
fluid mechanics; internal weapon bay; weapon release; overset mesh; SST DES model; smooth pseudo Winger-Vile distribution
2016-05-03
国家自然科学基金项目(11172283)
张群峰(1972—),男,讲师,博士。E-mail: zhangqunfeng@263.net
V211.3
A
1000-1093(2016)12-2366-11
10.3969/j.issn.1000-1093.2016.12.024
