计及负荷和电价不确定性的电力零售公司购电组合优化

2017-01-06陈玮梁博淼蒙文川陈政文福拴

电力建设 2016年7期

陈玮，梁博淼，蒙文川，陈政，文福拴

(1.中国南方电网公司，广州市 510623；2.新南威尔士大学商学院，澳大利亚悉尼市 NSW2052；3.南方电网科学研究院，广州市 510080；4.浙江大学电气工程学院，杭州市 310027；5.文莱科技大学电机与电子工程系，文莱斯里巴加湾 BE1410)

陈玮1，梁博淼2，蒙文川3，陈政3，文福拴4,5

随着我国电力市场改革的深化，售电侧随之逐步开放，已经成立了很多售电公司并参与了电力零售业务。如何构造在多个市场的购电组合优化策略是电力零售公司关注的重要问题。为发展电力零售公司的购电组合优化策略，必须适当考虑负荷需求和市场电价的不确定性从而进行风险管理。在此背景下，首先以h为单位构造了描述1天内的负荷需求和电力价格的日向量，并采用区间数来描述负荷和电价的波动范围。另一方面，模拟了零售公司在用户侧实施分时电价时对负荷调整和所占市场份额的影响。之后，以电力零售公司日利润总和最大为目标，建立了购电组合优化的强化区间线性规划(enhanced interval linear programming，EILP)模型，并采用解析方法求解。最后，采用美国PJM (Pennsylvania，New Jersey，Maryland)电力市场的负荷和电力价格实际数据，对所提出的方法做了说明。

电力市场；电力零售；购电组合优化策略；风险管理；负荷转移；强化区间线性规划(EILP)

0 引言

售电市场开放是电力市场改革的重要内容。从电力市场建设的国际实践来看，售电市场开放有助于降低用电成本，优化能源结构，进而改善电力系统的安全与经济运行。对于电力零售公司而言，如何在考虑负荷和电价不确定性的情形下构造最优购电组合策略以适当管理风险是值得研究的重要问题。在这方面，国内外近年来已有一些研究报道。

文献[1]建立了计及分布式发电的电力零售公司运营模型，采用两阶段分层模型分别模拟日前市场和实时市场，且实时市场模型以日前市场决策为边界条件，以实现运营费用最小化或收益最大化为目标。文献[2]着重探究我国目前的需求侧资源和需求响应现状，并从理论、技术和政策3个方面提出了售电侧开放条件下，我国需求侧资源参与电力市场的相关运营机制建议。文献[3]针对电力零售公司在日前市场的决策问题，基于历史数据采用ARMA(autoregressive moving average)模型预测负荷和电价，并利用CVaR (conditional value at risk)分析获得最优购电策略。文献[4-8]研究了电力零售公司的购电组合问题，并从不同角度，采用不同方法进行了探讨，分析了相关金融风险。其中，文献[4]采用了历史模拟法计算VaR (value at risk)；文献[5]导出了考虑分形分布情形下度量VaR风险的计算公式，并采用美国加州电力市场上网电价数据进行了实例分析；文献[6]采用购电收益函数的三阶矩阵(即偏度)来评估风险价值以量化零售公司的运营风险；文献[7]将售电主体分为拥有发电资产的售电企业和不拥有发电资产的售电企业，利用Bertrand寡头博弈模型分析这2类售电企业的定价策略；文献[8]则基于多重分形回归间隔分析来计算电力市场风险价值并进行购电组合风险优化。文献[4-8]的研究中均未考虑分时电价可以引起的负荷转移，进而削峰填谷。采用实时或分时电价可以有效促进负荷响应，改善负荷轮廓，降低供电成本。在现有的非固定电价机制中，实施难度较小的是分时电价[9]。文献[10-11]从期权角度对电力零售公司的经营策略进行分析。其中，文献[10]针对购电期权分析了在实时电价和用户需求随机变化时，期权合同购买方的最优期权合同组合策略；文献[11]定义了断电期权并分析了其在售电公司规避风险问题中的作用。比较而言，文献[10]侧重于零售公司与上游批发市场主体的互动，而文献[11]则注重零售公司与末端客户的交互。文献[12]基于分时电价和需求侧响应，探讨了购电风险的合理分摊，并利用CVaR就对冲合同优化在抑制风险方面的收效进行评价。文献[13]探讨了电力零售公司在分时电价环境下的运营优化策略。

现有文献中所提出的方法多数基于对未来数据的预测来制定购电组合策略，且一般假设负荷和电价服从某种概率分布如正态分布，而合适的概率分布形式并不容易确定。作为一种新的尝试，首先采用区间来表示负荷和电价，一般而言区间范围比概率分布更容易确定。之后，针对采用分时电价的电力市场，计及其在削峰填谷方面的作用，构建了零售公司在竞争电力市场中的购电优化策略的强化区间线性规划(enhanced interval linear programming，EILP)模型，并采用解析方法求解。

1 区间数理论及强化区间线性规划

1.1 简介

现有描述不确定性信息的方法主要包括概率、模糊和区间数等。其中，区间数适用于描述只知道参数的取值区间，无法确定分布的不确定信息，此时采用区间数表示，则可避免采用概率或模糊数表示时由于难以确定分布函数或隶属函数所可能导致的主观误差和系统误差[14]。对于基于区间数的优化决策问题，决策信息也将以区间数的形式给出。在二元和三元区间数的基本运算、排序、优化决策方面已取得了很多研究成果[15]。

对于区间数y±=[y-,y+]∈R±，y-和y+分别被称为区间数y±的小元和大元，且y+≥y-。可对区间数进行加法运算、倍数运算、乘法运算等，二元区间数的乘法运算的定义为

(1)

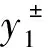
(2)

含区间数的非齐次线性方程组的计算法则与普通方程组的计算法则相似。通过由区间数组成的参数矩阵间的矩阵运算，可求得含区间数的非齐次线性方程组的解。即对于含区间数的矩阵运算，可按照矩阵运算法则结合区间数运算法则来计算。由区间数组成的n维向量Y±的定义为

(3)

1.2 负荷与电价的区间表示

为模拟分时电价环境下零售公司的收益和风险，以及用户针对分时电价所做出的负荷转移，下面针对以h为交易时段的1日24 h定义描述购电组合决策中的相关参量和变量的日向量。

设零售公司在次日24 h某市场中的购电价格和购电比例分别为24维列向量Pk和Mk。其中，Pk=[pk,1，…，pk,t，…，pk,24]T，其中k表示市场类型，k= c、d、r分别表示合约市场、日前市场和实时市场。Mk=[mk,1，…，mk,t，…，mk,24]T。给定次日市场中24 h的负荷需求用24维列向量L表示。

零售公司在制定购电决策时，次日负荷需求和实时市场的电价是不确定的。首先用区间数表示这2个量可能的变化范围，然后在计及负荷和实时电价不确定性的情形下确定零售公司的最优购电策略模型，进而采用EILP算法求取区间形式的购电优化决策结果。

1.3 强化区间线性规划

Moore于1966年在文献[16]中提出了区间分析方法，用于解决自动控制中存在的计算误差问题，之后于1993年提出了得到广泛应用的区间线性规划(interval linear programming，ILP)及其耦合模型[17]。实际中有很多变量和参数适于或便于用区间形式表示。文献[18-19]针对不确定性优化提出了改进区间线性规划(modified interval linear programming，MILP)和EILP的理论模型和求解算法，并论证了这2种模型解空间的绝对可行性。EILP模型在MILP的基础上提出了“适宜区间”概念，有效降低了优化结果的误差。本文将EILP模型及其算法应用于零售公司购电组合优化决策。

区间线性规划模型的一般形式为：

(4)

(5)

式中：X±为决策变量；A±为不等式约束系数；B±为常数项；C±为目标函数系数；I±为目标函数值，且

(6)

在求解EILP模型时，通过引入“适宜区间”D±将式(4)转换为2个交互式子模型进行求解。设相应的可行域为Q±，求解2个交互子模型可各得到一组适宜区间和可行域组合，分别为{D+，Q+}和{D-，Q-}。在构建交互子模型时，保持D+及可行域Q+所得的结果与原算法相同，对D-及可行域Q-进行修改，添加相应约束，即可确保解空间的绝对可行，如定理1所述[18-19]。

(7)

式中η满足：

在求得适宜区间D±的范围后，即可求取目标函数值的期望值，如式(8)所示：

(8)

2 分时电价、负荷转移及市场份额

2.1 分时电价方案

(9)

可构成电价向量ρ=[ρ1,…,ρt,…,ρ24]T。

2.2 零售公司的市场份额

在存在多个零售公司的电力市场环境中，用户可以自主选择任一家零售公司作为自己的电力供应商；另一方面，零售公司也可以采用多种价格策略来吸引自己的目标用户[20]。零售公司所占市场份额不仅对其收益有重要影响，也决定其市场影响力。设某零售公司所占市场份额为Sρ，其取值在一段时期内保持稳定，可定义为

(10)

式中：lt为时段t的原始负荷需求；Qt为该零售公司所承运的负荷总和。

已有研究表明，价格是影响用户作出改变供应商决定的最主要因素，所以零售公司采用的价格策略会在很大程度上影响其市场份额[21-22]。不同用户的行为特点和消费习惯一般也不同，如存在“忠诚客户”和“投机客户”等。“投机客户”是否选择某家零售公司与其价格的相对高低有相当大的关系。参照文献[3]和文献[23]，可用式(11)模拟多家零售公司的市场份额。

(11)

式中：β1和β2分别为该零售公司忠诚客户所占比例和其他电力零售公司忠诚客户所占比例；ωz(z=1，2，…，Z)是与电价相关的关联系数，用于表征因价格因素所引发的客户流动；ferr(x)为误差函数；oz和σz分别为该时段市场电价的均价和标准差。

式(11)模拟了同类零售公司、客户类型(忠诚度)、电价波动等对所研究的零售公司市场份额的影响。忠诚客户与其他影响因素的关联较弱，而价格对非忠诚客户选择零售商具有重要影响。

2.3 负荷调整与负荷转移行为模拟

在分时电价模式下，用户可以通过响应分时电价节约电费成本，主要方式为负荷转移，即将价格较高时段的负荷转移到较低时段。文献[24]提出了在以h为单位的实时电价模式下的负荷线性转移模型，并在文献[3]中经简化后用于对分时电价下的负荷转移行为进行模拟。对于时间跨度较长，如隔1日甚至数日的负荷转移，由于其成因较为复杂且较难界定，这里不予考虑。本文所讨论的负荷调整或负荷转移针对1个自然日进行。考虑到分时电价参数在较长时间段内保持恒定，可基于文献[24]模型定义负荷转移前后，每小时用电量变化情况。

(12)

3 问题描述与求解

3.1 基于区间数的电力零售公司购电决策优化的EILP模型

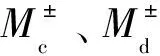
(13)

以日购售电利润总和最大为目标，建立式(4)所描述的零售公司购电决策优化模型，且零售公司在合约市场、日前市场、实时市场的购电比例之和为1，即

(14)

零售公司在日前市场和实时市场中可以按小时购电。另一方面，零售公司的合约购电一般是长期的，可以按照预先商定的合约分解方法把电量分配到每个时段，可认为具体到某日是定值。设Qc,t为分解到一日内某时段的合约购电量，即有

(15)

Qc,min≤λ±=[λ-,λ+]≤Qc,max

(16)

此外，在日前市场和实时市场的购电比例的波动范围可描述为

(17)

(18)

首先将零售公司购电组合优化策略模型转换为标准的EILP模型，进而采用1.3节中所述方法求解。由式(14)—(16)可知，决策向量不具备线性无关性，且可行域差异较大，故按式(19)—(22)进行处理。

(19)

(20)

(21)

(22)

将式(19)—(22)代入式(13)可得

(23)

即有

(24)

(25)

其中，目标函数的参数向量K′为

(26)

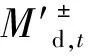
0≤λ′±≤1

(27)

(28)

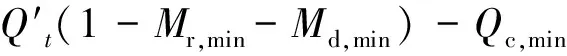
(29)

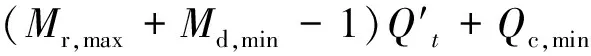
(30)

至此得到零售公司购电组合优化决策的标准EILP模型。之后即可用下述EILP算法对其进行求解。

3.2 EILP的求解方法和步骤

采用区间数描述负荷和电价不确定性的零售公司购电组合优化策略的EILP模型的求解步骤如下。

(1)采集负荷和电价数据，考虑分时电价、负荷转移、市场份额等影响因素，构建零售公司购电组合优化策略模型如式(13)—(18)所示。

(2)采用式(19)—(22)对上一步得到的模型进行标准化处理，得到式(4)所描述的购电组合优化策略EILP模型。

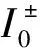
基于上述算法，采用Matlab编制了计算程序。

4 算例分析

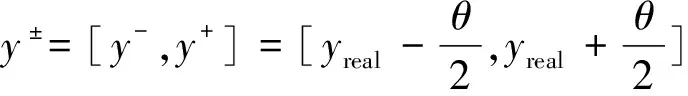
设零售公司每天分3个时段对用户计价：(1)午夜00：00点至早上07：00点按低谷电价计费，电价为γ1=35 $/( MW·h)，时长T1=7 h；(2)早上07：00点至晚上22：00点按峰时电价计费，电价为γ2=50 $/( MW·h)，时长T2=15 h；(3)晚上22：00点至午夜00：00点按低谷电价计费，电价为γ3=35 $/(MW·h)，时长T3=2 h。针对该分时电价机制，用户会对用电负荷进行调整或转移，以期在不影响生产或生活的前提下节约电力支出。对于峰荷时段(即早上07：00点至晚上22：00)，电力需求将向价格低谷时段转移，设转移比率为0.08；低谷时段(即午夜00：00点至早上07：00点，以及晚上22：00点至午夜00：00点)，吸纳由峰荷时段转移出来的电力需求，设价格低谷时段吸纳峰荷的流入比率为0.15。由于峰荷时段为15 h，2个低谷时段总共9 h，且峰荷时段的负荷基数更大，这样峰荷时段的负荷转移比率就小于低谷时段所吸纳峰荷的流入比率。这样，负荷转移弹性标量指数α(t1,t2)可用式(31)确定。

(31)

式中：下标p和v分别表示峰时电价时段和低谷电价时段；Λv和Λp分别为低谷电价时段集合和峰时电价时段集合。

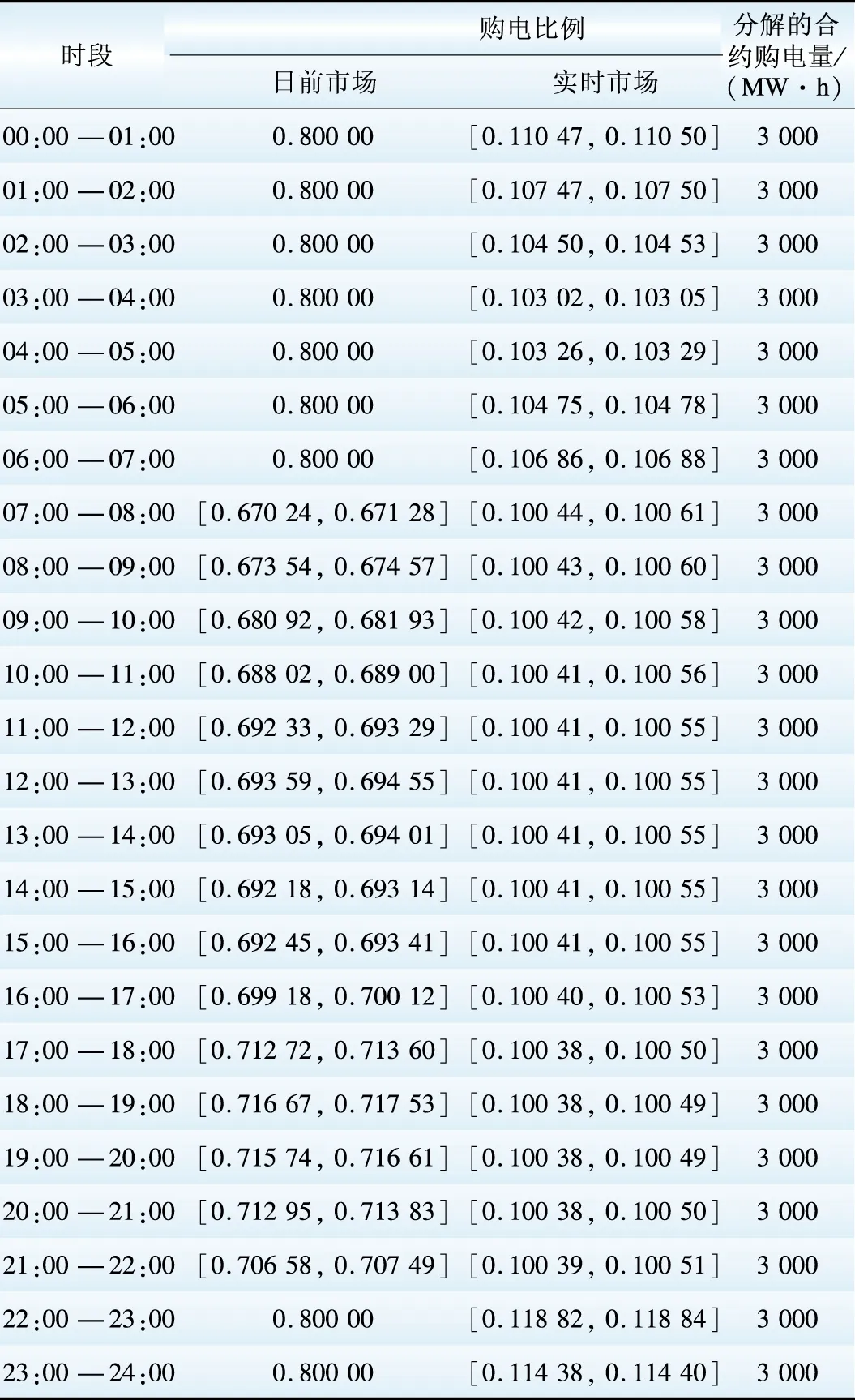
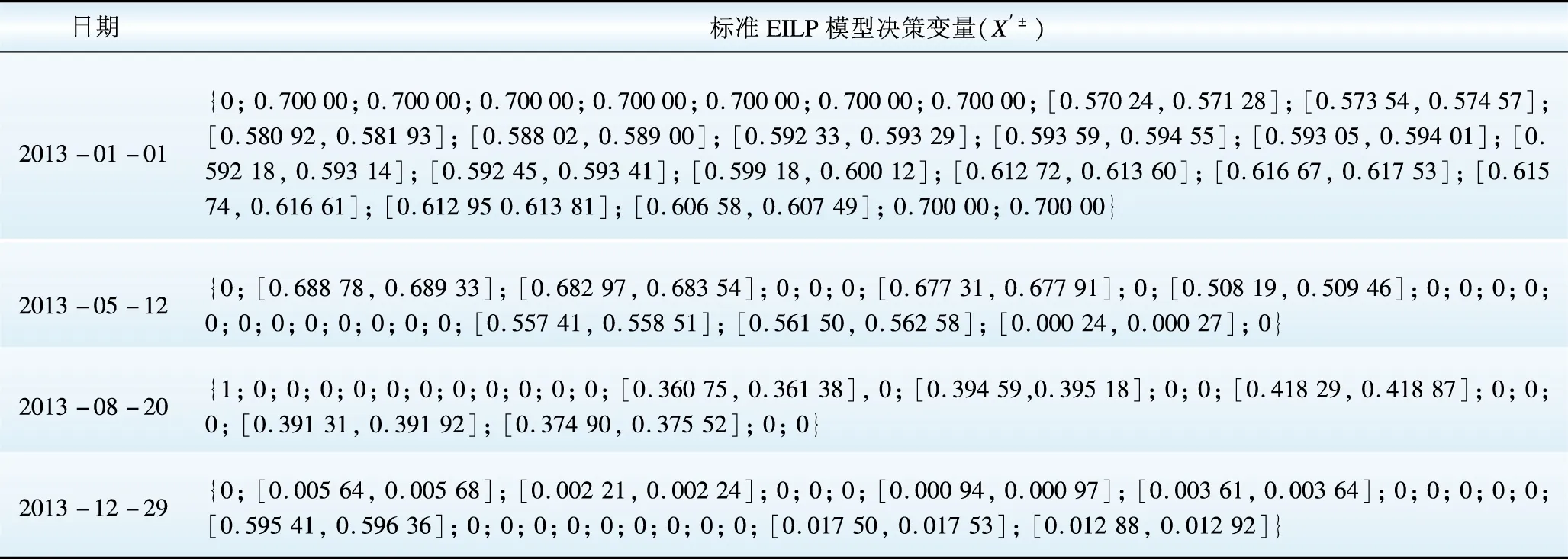
给定β1=0.1，β2=0.2；ω1=0.7，ω2=1，ω3=0.7；o1=34，o2=49，o3=37；σ1=2，σ2=3，σ3=2。则根据分时电价数据和式(11)可求得零售公司所占市场份额Sγ。给定θL=10，θP=2，Qc,min=3 000 MW·h，Qc,max=8 000 MW·h，Md,max=0.8，Md,min=0.1，Mr,max=0.8，Mr,min=0.1，合约购电价Pc=30 $/( MW·h)，分别对所选4日进行购电组合优化，得到的优化结果见附表A4。采用式(24)可求得购电组合优化结果相应的零售公司利润，如表1所示。以2013-01-01为例进行去标准化，可得到表2所示的具体购电组合决策方案。

表1 零售公司最优购电组合策略对应的期望利润
Table 1 Expected profit of optimal purchasing strategy of electricity retail company

表2 电力零售公司最优购电组合方案(2013-01-01)Table 2 Optimal purchasing portfolio schemes of electricity retail company on January 1, 2013

以2013-01-01为例，分析区间数据特性对零售公司盈利的影响。

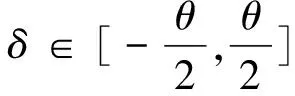
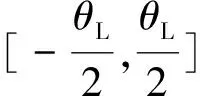
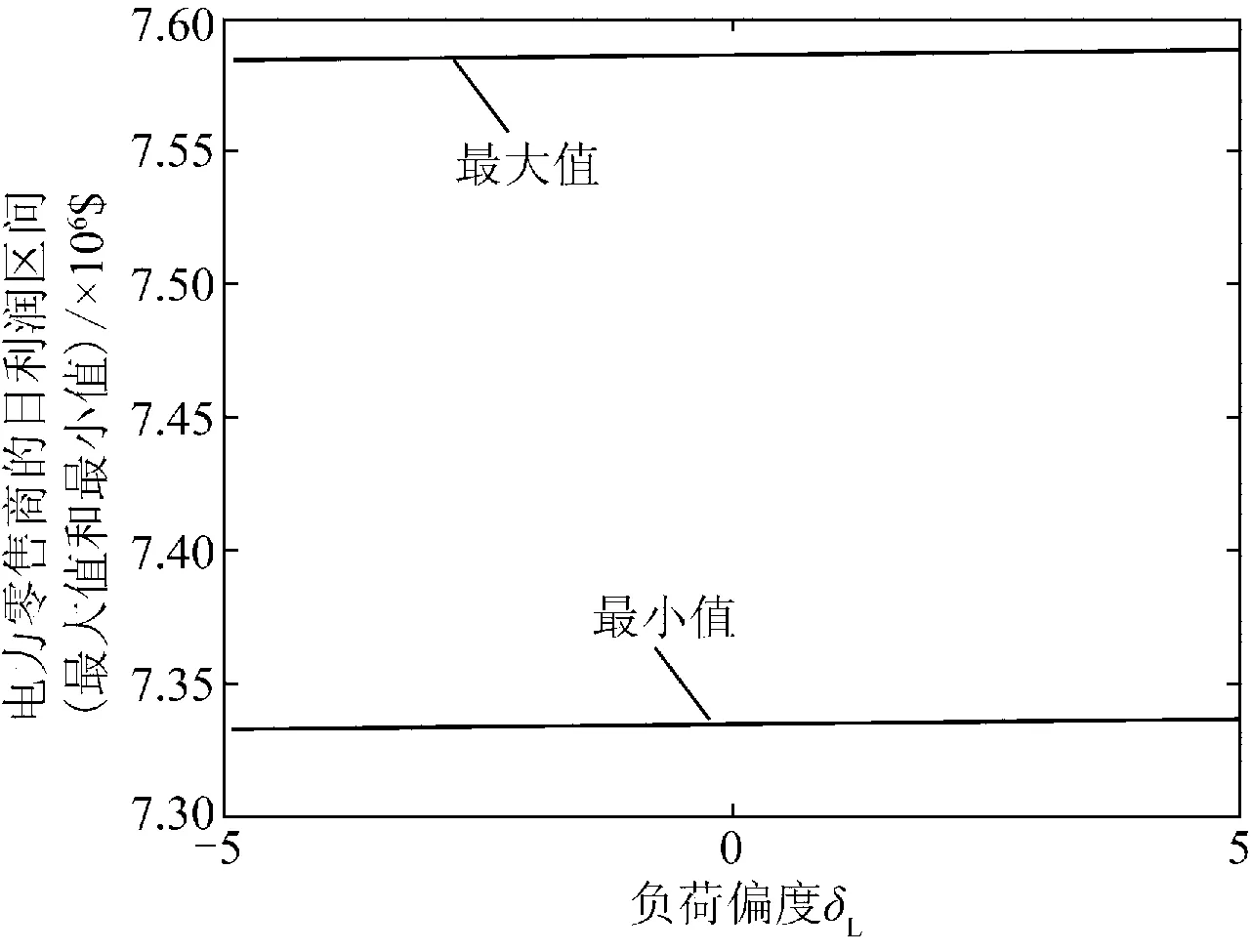
接着分析区间量范围变化对盈利的影响。当θL和θP分别在[0，100]和[0，4]区间内变化时，以θL为x轴，θP为y轴，零售公司利润为z轴，三者的变化关系如图3所示。

区间范围越小，不确定程度越低，反之亦然。从图3可以看出，负荷和实时电价的区间范围越大，零售公司获利所面对的风险越大。

由表1可以看出，采用EILP算法获得的利润区间比较小，即利润分布比较密集，且可以根据“适宜区间”获得日利润的期望值，这可为零售公司确定购电组合决策提供技术支持。

图3 零售公司的利润受θL和θP区间变化的影响Fig.3 The impacts of interval range changes ofθL and θP on the profit of the electricity retail company

5 结论

针对电力零售公司在合同市场、日前现货市场和实时市场的日前最优购电组合策略问题，首先采用区间数来描述次日各个时段的电力负荷和实时市场电价，采用这种方法处理不确定性比较简单和现实。在用户侧，模拟了零售公司对用户采用分时电价时可能导致的用电负荷调整或转移，以及对零售商市场份额的影响。在此基础上，构造了强化区间线性规划模型。用美国PJM电力市场的实际负荷和实时市场数据对所提出的模拟和方法做了说明，分析了用于描述电力负荷和实时市场电价的区间数的偏度和范围对零售公司收益的影响。

电力零售公司的运营策略是一个极其复杂的问题，需要考虑从多个市场的购电策略、向用户的售电策略、购电功率和用户功率的匹配、其他零售公司购售电策略的影响等，涉及大量不确定因素。随着国内电力售电市场的逐步开放，这个问题已经引起广泛关注。本文只是做了些初步的工作，尚有很多问题有待深入研究。

[1]ALGARNI A A S，BHATTACHARYA K. A generic operations framework for discos in retail electricity markets[J]. IEEE Transactions on Power Systems，2009，24(1)：356-367.

[2]赵岩，李博嵩，蒋传文. 售电侧开放条件下我国需求侧资源参与电力市场的运营机制建议[J]. 电力建设，2016，37(3)：112-116. ZHAO Yan，LI Bosong，JIANG Chuanwen. Operation mechanism suggestions of demand-side resources in electricity market under retail power market deregulation in China[J]. Electric Power Construction，2016，37(3)：112-116.

[3]HATAMI A，SEIFI H，SHEIKH-EI-ESLAMI M K. A stochastic-based decision-making framework for an electricity retailer: time-of-use pricing and electricity portfolio optimization[J]. IEEE Transactions on Power Systems，2011，26(4)：1808-1816.

[4]周浩，张富强. 采用VaR历史模拟方法计算电力市场短期金融风险[J]. 电力系统自动化，2004，28(3)：14-18. ZHOU Hao，ZHANG Fuqiang. Calculation of short-term financial risk in electricity market by VaR historical simulation method[J]. Automation of Electric Power Systems， 2004，28(3)：14-18.

[5]王绵斌，谭忠富，张蓉. 分形VaR风险度量下的购电组合模型及实证分析[J]. 电力系统及其自动化学报，2009，21(6)：11-16. WANG Mianbin，TAN Zhongfu，ZHANG Rong. Purchase power portfolio model and an empirical analysis based on risk measure with fractal value-at-risk[J]. Proceedings of the CSU-EPSA，2009，21(6)：11-16.

[6]陈彦州，赵俊华，文福拴，等. 偏度风险价值下供电公司/电力零售公司动态购电组合策略[J]. 电力系统自动化，2011，35(6)：25-29. CHEN Yanzhou，ZHAO Junhua，WEN Fushuan，et al. A skewness-VaR based dynamic electricity purchasing strategy for power supply companies/retail companies[J]. Automation of Electric Power Systems，2011，35(6)：25-29.

[7]黄伟，李玟萱，李宁坤，等. 基于Bertrand模型的两类售电企业定价策略[J]. 电力建设，2016，37(3)：76-81. HUANG Wei，LI Minxuan，LI Ningkun，et al. Pricing strategy for two kinds of electricity retail companies based on Bertrand model[J]. Electric Power Construction，2016，37(3)：76-81.

[8]刘伟佳，尚金成，周文玮，等. 基于多重分形理论的电力市场风险价值评估[J]. 电力系统自动化，2013，37(7)：48-54. LIU Weijia，SHANG Jincheng，ZHOU Wenwei，et al. Evaluation of value-at-risk in electricity markets based on multifractal theory[J]. Automation of Electric Power Systems，2013，37(7)：48-54.

[9]YANG W，YU R，NAMBIAR M. Quantifying the benefits to consumers for demand response with a statistical elasticity model[J]. IET Generation，Transmission and Distribution，2014，8(3)：503-515.

[10]盛方正，季建华. 多种期权合同条件下的供电公司最优购电策略[J]. 电力系统自动化，2007，31(12)：36-39，107. SHENG Fangzheng，JI Jianhua. Optimal purchasing strategy of the electricity supply company under multi-options[J]. Automation of Electric Power Systems，2007，31(12)：36-39，107.

[11]盛方正，季建华. 基于断电期权的供电公司购电价格风险管理方法[J]. 电力系统自动化，2007，31(18)：30-33. SHENG Fangzheng，JI Jianhua. Method of managing power supplier’s price risk of purchasing electricity based on interruptible options[J]. Automation of Electric Power Systems，2007，31(18)：30-33.

[12]ZHANG Q，WANG X. Hedge contract characterization and risk-constrained electricity procurement[J]. IEEE Transactions on Power Systems，2009，24(3)：1547-1558.

[13]ÇELEBI E，FULLER J D. A model for efficient consumer pricing schemes in electricity markets[J]. IEEE Transactions on Power Systems，2007，22(1)：60-67.

[14]张兴芳，管恩瑞，孟广武. 区间值模糊综合评判及其应用[J]. 系统工程理论与实践，2001(12)：81-84. ZHANG Xingfang，GUAN Enrui，MENG Guangwu. Interval-valued fuzzy comprehensive evaluation and its application[J]. Systems Engineering-Theory & Practice， 2001 (12)： 81-84.

[15]胡启洲，张卫华. 区间数理论的研究及其应用[M]. 北京：科学出版社，2010.

[16]MOORE R E. Interval analysis[M]. New York：Prentice-Hall，1966.

[17]HUANG G，DAN MOORE R. Grey linear programming，its solving approach，and its application[J]. International Journal of Systems Science，1993，24(1)：159-172.

[18]周丰，陈国贤，郭怀成，等. 改进区间线性规划及其在湖泊流域管理中的应用[J]. 环境科学学报，2008，28(8)：1688-1698. ZHOU Feng，CHEN Guoxian，GUO Huaicheng，et al. Modified interval linear programming for lake water shed management[J]. Acta Scientiae Circumstantiae，2008，28(8)：1688-1698.

[19]周丰，郭怀成. 不确定性非线性系统“模拟-优化”耦合模型研究[M]. 北京：科学出版社，2010.

[20]CARLSON J A， MCAFEE R P. Discrete equilibrium price dispersion[J]. The Journal of Political Economy，1983，91(3)：480-493.

[21]STANTON P J，CUMMINGS S，MOLESWORTH J， et al. Marketing strategies of Australian electricity distributors in an opening market[J]. Journal of Business & Industrial Marketing，2001，16(2)：81-93.

[22]MULLER M，SENSFUB F，WIETSCHEL M. Simulation of current pricing-tendencies in the German electricity market for private consumption[J]. Energy policy，2007，35(8)：4283-4294.

[23]HANSSENS D M，PARSONS L J，SCHULTZ R L. Market response models：econometric and time series analysis[M]. New York：Springer Science & Business Media, 2003.

[24]SCHWEPPE F C，CARAMANIS M C，TABORS R D，et al. Spot pricing of electricity[M]. New York：Springer Science & Business Media, 2013.

(编辑景贺峰)

附录A

表A1 PJM电力市场2013年4 日中每个时段的负荷量数据
Table A1 Hourly load in PJM electricity market in 4 days of 2013 MW·h

表A3 PJM实时电力市场2013年4 日中每个时段的电价数据Table A3 The real-time electricity prices in PJM day-ahead electricity market in 4 days of 2013 $·(MW·h)-1

Optimal Portfolio Strategies of Purchasing Electricity for Electricity Retail Companies Considering Load and Electricity Price Uncertainties

CHEN Wei1，LIANG Bomiao2，MENG Wenchuan3，CHEN Zheng3，WEN Fushuan4,5

(1. China Southern Power Grid, Guangzhou 510623, China; 2. Business School, University of New South Wales, Sydney NSW2052, Australia; 3. Electric Power Research Institute of China Southern Power Gird, Guangzhou 510080, China; 4. School of Electrical Engineering, Zhejiang University, Hangzhou 310027, China; 5. Department of Electrical and Electronic Engineering, Universiti Teknologi Brunei, Bandar Seri Begawan BE1410, Brunei)

With the development of electricity market reform, electricity retail markets are established and many electricity retail companies are gradually built up and involved in electricity retail business. How to build the optimal portfolio strategies for purchasing electricity by an electricity retail company in multiple markets is an issue with extensive concern. To this end, it is necessary to consider the uncertainties of load demand and electricity prices in the market environment so as to manage risk associated. Given this background, two vectors representing hourly load demands and electricity prices in the real-time electricity market are first employed for a specified day, and interval numbers are used to represent the fluctuation range of load and electricity price. On the other hand, the impacts of the time-of-use (TOU) retail electricity price for terminal users on the load shift and market share of the electricity retail company concerned are investigated. Then, an enhanced interval linear programming (EILP) model is presented with the objective of maximizing the overall profit of the electricity retail company in a given day, and solved by an analytic approach. Finally, actual load and electricity price data from the PJM (Pennsylvania, New Jersey, Maryland) electricity market in USA are employed to demonstrate the presented method.

electricity market; electricity retail; portfolio strategies for purchasing electricity; risk management; load shift; enhanced interval linear programming (EILP)