微网系统鲁棒优化规划模型研究

曾鸣，杨雍琦，范世源，孙辰军

(1. 华北电力大学经济与管理学院，北京市 102206；2. 国网河北省电力公司，石家庄市 050000)

微网系统鲁棒优化规划模型研究

曾鸣1，杨雍琦1，范世源1，孙辰军2

(1. 华北电力大学经济与管理学院，北京市 102206；2. 国网河北省电力公司，石家庄市 050000)

分布式可再生能源发电出力的不确定性给微网系统的优化规划带来了较大困难。以分布式发电的实际出力偏差与预测偏差的差值为主要分析对象，刻画了系统的鲁棒性约束条件，构建以规划成本、运行成本为目标函数的微网系统鲁棒优化规划模型，并整合了相应的NSGA-II优化算法。通过算例分析证明，该文的鲁棒优化模型能够在一定鲁棒约束、系统运行约束条件下求解得到系统最优规划方案，从而为微网系统鲁棒优化规划提供决策依据。

微网；鲁棒优化；分布式发电；NSGA-II算法

0 引 言

近年来在国家各项支持政策、激励机制的扶持下，以分布式可再生能源为主要供能方式的微网取得了迅猛发展[1]。然而受到分布式可再生能源随机性、波动性等特征影响，微网系统的规划与运行都将面临严峻的不确定性，传统的、以确定条件为基础的微网规划运行模式已经难以解决当前的问题[2-3]。因此如何在系统规划阶段就充分考虑分布式发电出力的不确定性，使规划方案及相应的系统运行方案能够以最小的经济成本应对这种不确定性,并保证系统的安全可靠运行，是当前亟需研究的问题。

目前有关微网系统经济运行方面的研究已经较为成熟，包括多种优化调度模型、算法等。如文献[4]建立了负荷优化分配模型与负荷可中断优化模型，针对独立运行模式下的微网能量管理问题，提出微网实时能量优化调度方法。文献[5]构建了优化微网内分布式电源出力的数学模型，同时考虑对主网向微网输入功率的优化问题。文献[6]将需求侧处理成一种可以主动参与微网规划与运行的电源，构建了相应的微网综合资源规划模型。同时，作为处理不确定性的常用方法之一，目前已有将鲁棒优化与微网系统运行结合的相关研究。文献[7]利用风电出力的矩(均值和协方差矩阵)不确定性，构建出风电出力的矩不确定集合，建立微网系统的分布鲁棒经济调度模型。文献[8]构建了计及可再生能源、储能装置和热电联产系统的微电网经济运行鲁棒优化模型；通过改进常规细菌觅食算法中复制操作和驱散操作，有效兼顾了个体寻优过程中寻优速度与寻优深度。

从目前国内外相关文献来看，大部分研究内容是微网规划方案既定条件下的系统运行优化研究，在系统规划阶段就考虑分布式发电不确定性的相关研究较少。针对上述问题，本文拟通过预算约束刻画系统分布式可再生能源发电出力的不确定性，并将该约束与系统规划模型相结合构建微网系统鲁棒优化规划模型，求解得到能够应对发电出力不确定性的、规划及运行成本最小化的系统规划方案，从而为微网规划方案设计与选择提供决策依据。

1 微网规划及运行模型的构建

考虑到规划方案的可行与否必须要通过系统运行结果来验证，因此本文模型的目标函数包括2个部分：规划成本函数及运行成本函数。

1.1 目标函数

(1)系统规划成本：

(1)

式中：Cif，Cjw，CuPV，Cob分别为柴油机组(或火电机组)、风电、光伏机组及储能设备的单位容量投资成本；Qif、Qjw、QuPV、Qob分别为柴油机组(或火电机组)、风电、光伏发电机组投资容量及储能设备容量；此处忽略输配电成本。

(2)系统调度成本。系统调度过程分为日前调度与实时调度。

1)日前调度成本：

(2)

式中：CO,d为日前调度成本；δi表示柴油机组(或火电机组)i是否启用，取值为1时代表机组启用，0代表未启用；ci(qi,t)为机组燃料成本函数，其计算公式为

(3)

式中：qi,t为可调度机组的出力；ai、bi、ci为机组发电的成本系数；本文此处不考虑机组的停机和启动成本，忽略储能设备调动成本；对于风电和光伏的运行成本，本文采用电度成本计量，即cj、cu为风电、光伏的发电成本，元/(kW·h)；qj,t、qu,t为风电、光伏在t时间段内的发电出力(t以每h为1个时间段)；qb,grid为从主网购买的电量，pb,t为购电电价；qs,grid为向主网销售的电量，ps,t为售电电价。

2)实时调度成本：

(4)

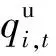
在日前调度过程中，对各个时间段的可再生能源发电出力进行预测，同时给出预计的预测偏差。然而在系统实时运行过程中，这个预测偏差与实际偏差之间仍存在差额，式(4)的第1个多项式就是刻画由于这个差额所产生的成本，是第2节鲁棒约束条件所主要考虑的因素。

1.2 分布式可再生能源出力模型及储能模型

1.2.1 分布式可再生能源出力模型

本文的风电及光伏发电出力模型采用国内常用的测算方法[9-10]。其中风电出力测算模型为

(5)

式中：qj(v)为风电出力功率；v为风速；qr为风机的额定功率；vc为切入风速；vr为额定风速；vf为切出风速。

光伏发电出力测算公式为

qu,t=LMθ

(6)

式中：qu,t为光伏发电出力功率；L为太阳辐照度；M为受光面积；θ为发电效率。

1.2.2 储能模型

储能设备的荷电状态(state-of-charge，SOC)与充放电功率的关系式如下：

(8)

(9)

式中：QSOCmax为储能设备的最大荷电状态；Rmax为储能设备的额定充放电功率；m和n为控制储能设备充放电的参数，根据国内外相关研究，m取值为20.52，n取值为0.55。

1.3 约束条件

(1)日前系统功率平衡约束：

(10)

式中：qLOSS为输电功率损耗；Dtotal为系统总负荷；qo,t为储能设备充放电功率，当储能设备放电时，取值为正，充电时取值为负；εt为每个时间段分布式发电出力偏差的预测值。

(2)日前节点功率平衡约束：

(11)

式中：qij,t和fij,t分别为节点j的可调度机组出力及分布式可再生能源发电出力；nz为j周边节点数量；σj,t和σz,t为节点j和z的电压相位角；dj,t为节点j处的负荷。该等式在任意的t时间段内成立。

(3)实时节点功率平衡约束：

(12)

Qds,t≤Qs,t

(13)

wj,t≤qj,t+qu,t+εt

(14)

(15)

(16)

公式(12)为系统实时运行时的功率平衡约束条件，式(13)表示可中断负荷的偏差值要小于预计可中断负荷，式(14)表示弃风弃光出力小于风电光伏总出力加上误差值。

(4)发电出力及储能设备约束条件：

qimin≤qi,t≤qimax

(17)

0≤qj,t≤qjmax

(18)

0≤qu,t≤qumax

(19)

式中：qimin和qimax为柴油机组(或火电机组)出力上、下限；qjmax和qumax为风电和光伏机组出力上限。该约束条件要求各类机组的出力需保持在上下限之内。

同时要求：

-vi,dΔtud≤Δqi,t≤vi,uΔtud

(20)

式中：Δqi,t为机组i的出力变化；vi,d和vi,u为柴油机组i(或火电机组)单位时间内的最大上升和下降速率；Δtud为这个时段所持续的时间。式(20)代表机组的出力变化需保持在其最大上升和下降速率之间。

(5)储能设备充放电约束：

(21)

QSOCmin≤QSOCt≤QSOCmax

(22)

(23)

(24)

2 微网系统鲁棒性刻画

从第1节的模型构建可以看出，本文共包括3个目标函数，是一个多目标优化问题，而第3个实时调度目标函数考虑到了分布式发电的实际出力偏差与预测偏差，而本文各规划方案能否应对分布式发电不确定性的关键是在预测偏差与实际偏差之间的差额最大时，实现成本的最小化[13]。因此目前的目标函数(公式(4))是一个最大值最小化问题，此时引入ψ作为“预算约束”、ξ作为空间相关性约束，构建鲁棒约束条为：

(25)

(26)

(27)

(28)

用向量来表示目标函数及相关约束条件：

(30)

wa=-Δε-Qb

(31)

qa≤1-qx-Δε

(32)

q≤M

(33)

下面我们将该目标函数转化为混合整数线性规划问题，引入向量η、θ和γ并整合进行拉格朗日变换得：

(34)

0≤γ⊥q-M≤0

(35)

MTγ=-η-qTθ

(36)

(37)

θ≥0

(38)

将约束条件(25)—(29)引入，并联合式(34)进行拉格朗日变换后，将式(34)展开，可得：

(39)

同时还包括以下约束条件：

(40)

(41)

ηj+ωs,t≤Qds,t

(42)

经过上述一系列公式变换，可得新模型的目标函数为

minCP,CO,d,CO,t

(43)

约束条件为式(10)—(24)、式(25)—(29)和式(40)—(42)。同时对偶变量ωs,t、φt、ρj都大于0。

3 算法选择及改进

本文共包括3个目标函数，但是在求解过程中，并不是实现3个目标函数同时最优，而是分步骤进行计算，首先计算日前调度模型，根据实时调度过程中的偏差计算实时调度模型，最后根据前2个模型求解得到的机组出力组合再求解规划成本模型。

本文将采用NSGA-II算法求解，其具体求解流程见文献[14]，作为常用求解方法之一，其常规过程本文不再赘述。然而考虑到上述求解过程，本文的NSGA-II算法并不需要对具体的交叉、变异操作做修改，而是需要对求解流程做部分修改，要求使用2次选择、交叉和变异的操作，并执行多次计算。修改后的流程图见图1。

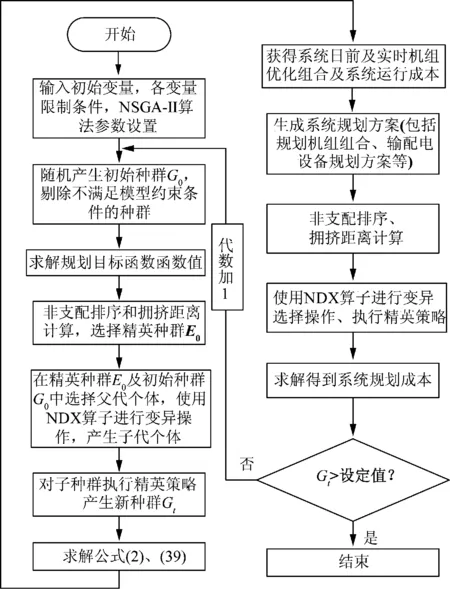
图1 模型求解过程Fig.1 Model solving process

4 实证分析

4.1 系统参数

本文将对文献[15]中的IEEE 13母线系统进行改进，改进后的节点系统如图2所示。

图2 改进后的IEEE 13母线系统图Fig.2 Modified IEEE 13 bus system

图2中节点6、7、9为可中断负荷，其上下限参见表1，对于参与实时调度过程的可中断负荷，按照2元/kW的价格进行补偿，同时假设微网系统从主网购电电价为0.8元/(kW·h)，售电电价为0.5元/(kW·h)。

表1 可中断负荷参数
Table 1 Interruptible load parameters

kW

系统负荷曲线如图3所示。

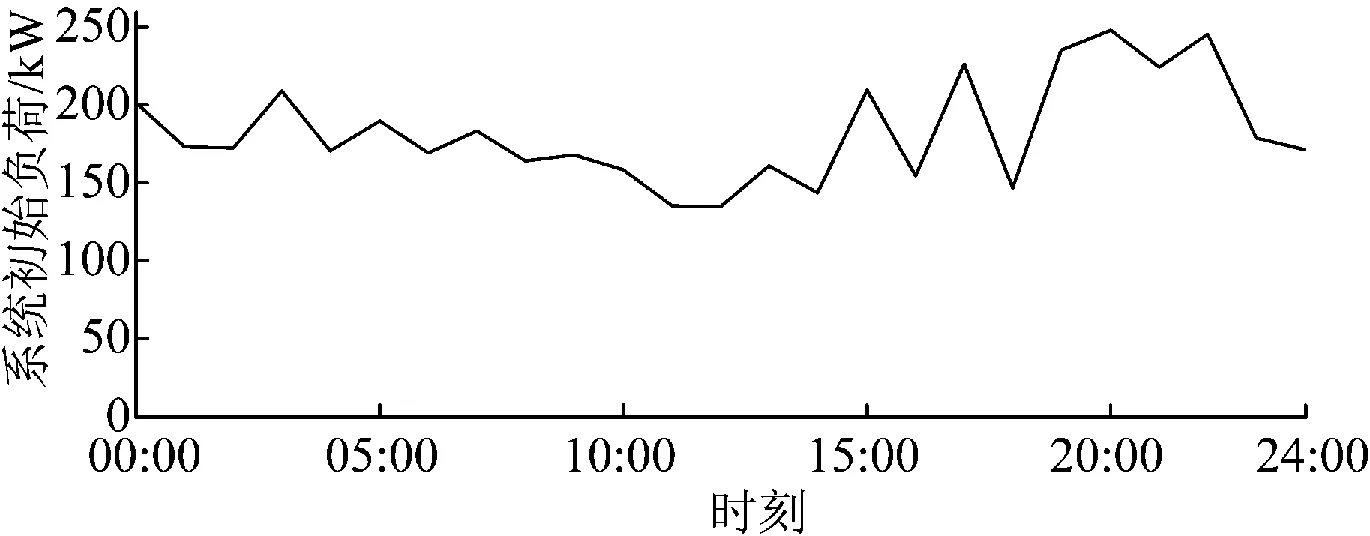
图3 系统总负荷曲线Fig.3 Total load curve of system

算例中共有3个电源点，主要的可调度机组为柴油机组，此处设柴油机组可在DG1与DG2电源点接入，光伏发电与小型风电机组可在DG2与DG3电源点接入。考虑到微网内部主要电力供应方式为分布式可再生能源发电，因此要求可再生能源占大部分，柴油机组不可同时在DG1与DG2电源点接入，因此柴油机组只能在DG1接入。则系统的电源规划方案见表2。

表2 电源规划方案
Table 2 Planning schemes of generation source

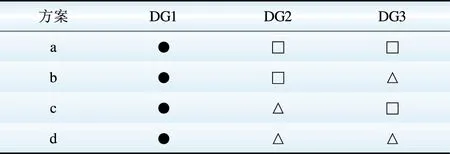
图中：“●”代表柴油机组；“□”代表小型风电；“△”代表光伏发电。柴油机组目前主要有2种型号可供选择，主要参数见表3。

风电机组包括2种，一类额定功率10 kW，购买价格10万元，另一类额定功率20 kW，购买价格14万元。切入风速为3 m/s，额定风速取11 m/s，切出风速取30 m/s。风电成本设为0.47元/(kW·h)，光伏发电成本设定为0.88元/(kW·h)。光伏发电按照6.5元/W计算，储能电池额定容量60 kW·h，成

表3 柴油机组参数
Table 3 Diesel generator parameters

本为2 000元/(kW·h)，本文将采用华北某地的负荷数据、风速数据和太阳辐照度数据来代入进行测算，风电成本设为0.47元/(kW·h)，光伏发电成本设定为0.88元/(kW·h)。

4.2 模型测算

综合国内外相关研究及IEEE13母线系统的相关数据，此处鲁棒预算约束参数ψ的取值为5.2，不同电源点之间的空间相关系数ξ取值见表4。

表4 空间相关系数取值
Table 4 Spatial correlation coefficient values

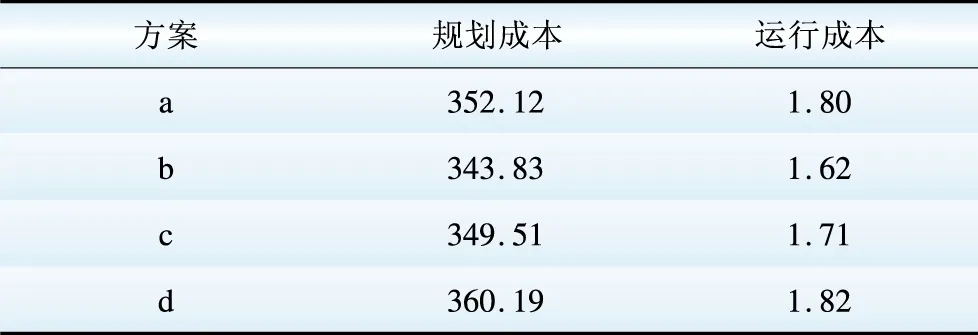
将已有数据代入模型，经200次迭代计算，以系统不出现切负荷情况为最基本要求，可得不同方案下的系统规划成本和系统运行成本见表5，其中系统运行成本为日前调度成本和实时调度成本之和。

表5 系统规划成本及运行成本 万元
Table 5 Planning cost and operation cost of system

各方案迭代收敛过程如图4、图5所示。

从迭代计算过程来看，如图4所示，计算各规划方案的运行成本时，4个方案约在75次迭代计算附近收敛到最优值；如图5所示，在计算运行成本计算时，4个方案约在100次迭代附近收敛到最优值。同时未出现切负荷情况，因此证明经过本文的模型测算，4个规划方案都是科学合理的，在可再生能源分布式发电并网的条件下具有鲁棒性。在本文的4个规划方案中，通过规划成本和运行成本的计算结果来做对比可知，方案b(柴油机组在DG1接入，小型风电机组在DG2接入，光伏发电机组在DG3接入)是最优规划方案。下面本文将对方案b做进一步的分析。

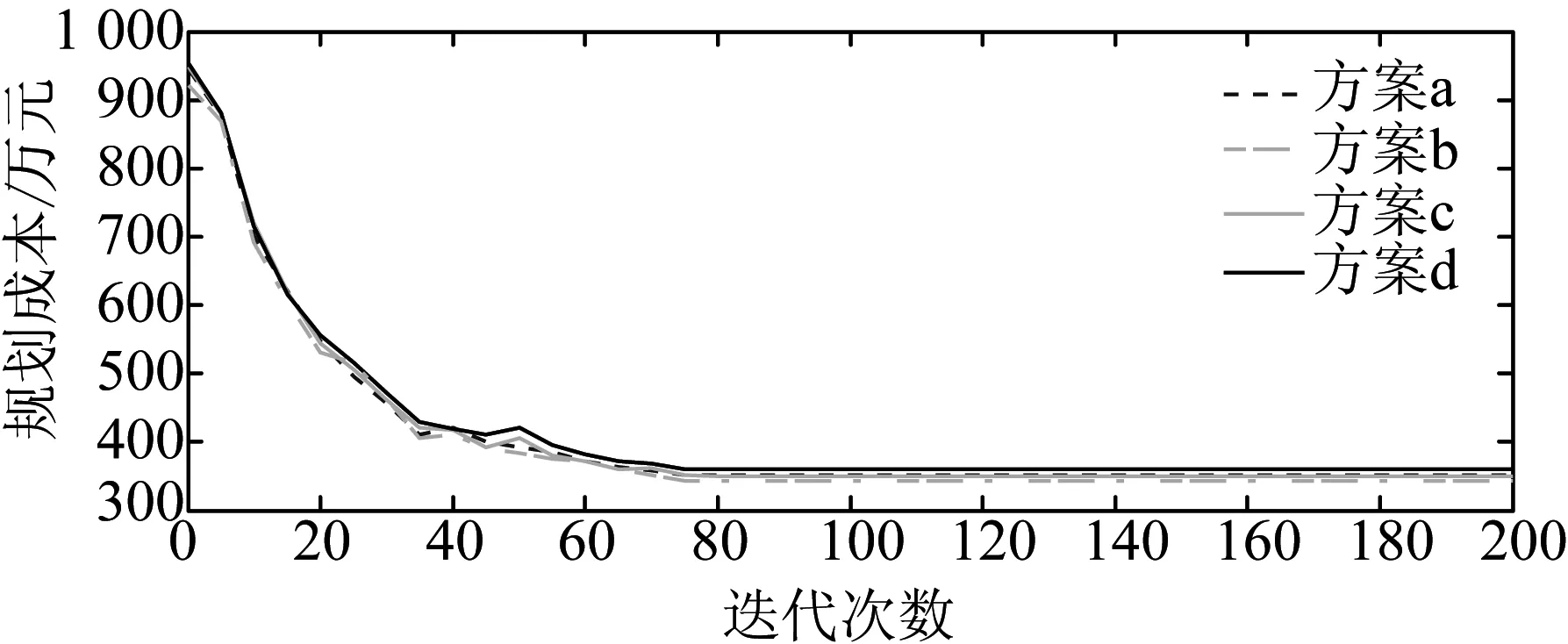
图4 各规划方案规划成本收敛过程Fig.4 Convergence process of planning cost in each planning scheme

图5 各规划方案运行成本收敛过程Fig.5 Convergence process of operation cost in each planning scheme

4.3 优化方案深入分析

通过对机组优化组合模型的深入计算，可以求得实时的系统各类型机组出力及负荷变化曲线如图6所示，系统储能设备充放电、调用用户可中断负荷、从主网购售电的变化趋势见图7。

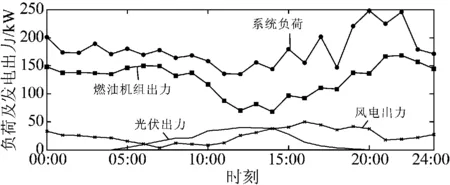
图6 机组出力及负荷变化Fig.6 Unit output and load change

图7 可中断负荷调用、主网购售电和储能设备充放电情况Fig.7 Results of interruptible load, power flow from main grid and charge and discharge of energy storage

将图6的系统负荷与初始系统负荷相比，在加入可中断负荷后，配合储能设备的智能充放电，风电、光伏等分布式可再生能源发电出力的反负荷调节特性显著缓解，同时加上从主网的购售电，使燃油机组的出力曲线更为平滑，能够在降低系统运行成本的基础上，提高系统的安全可靠性。

下面本文将以方案b为例，改变预算约束ψ的取值，以期进一步定性分析不确定约束取值大小与系统规划成本和系统运行成本之间的相互关系。此处从ψ=0开始取值计算，ψ=0时为确定系统(分布式可再生能源发电预测准确率100%，不存在任何偏差)，到ψ=15，此时对系统的鲁棒性要求较高为止，计算不同ψ取值下的系统规划成本及运行成本，计算结果如图8、9所示。

图8 系统运行成本变化趋势Fig.8 Trend of system operation cost

图9 系统规划成本变化趋势Fig.9 Trend of system planning cost

从图8—9可以看出，在ψ取值较小的区间内，随着ψ取值的增加，规划成本和运行成本的变化不大，运行成本在ψ取值大于3后开始随着ψ取值的增加而显著增加，规划成本则是在ψ取值大于1.5处。在ψ取值较大的区间内，规划成本和运行成本也不随着ψ的增加而一直增加，而是增加到一定程度后就不再增加。限于篇幅，此处可以对这种情况做初步的定性分析，ψ的取值较小时，系统为确定性较强的系统，能够以较小的成本增加幅度来应对每一单位ψ的取值变化；ψ的取值较大时，系统所要面对的不确定性最强，因而规划成本与运行成本也最高，则此时的系统与其他条件下的系统相比，较高的规划投入、运行投入带来了更为可控的发电资源、柔性更强的负荷，此时系统的鲁棒性达到峰值，已不需要增加过多的成本来应对不确定性。

5 结 论

本文构建了微网鲁棒优化规划模型，并提出了相应的求解算法，经过算例分析证明本文的模型能够在一定的鲁棒性、不出现切负荷情况的基本要求下，求解多个规划方案的规划成本及典型调度日的运行成本，并从中选择最优方案。同时针对该最优规划方案，测算不同预算约束取值条件下该方案的规划成本及运行成本。

限于篇幅，本文对随着预算约束取值增加所带来的系统规划成本、运行成本的变化趋势只做了初步的定性分析，未来有必要研究相应的模型及算法，详细深入分析二者之间的相互关系，为电力系统的规划方案设计提供更为坚实的理论依据和决策支撑。

[1]刘吉臻. 大规模新能源电力安全高效利用基础问题[J]. 中国电机工程学报, 2013, 33(16): 1-8. LIU Jizhen. Basic issues of the utilization of large-scale renewable power with high security and efficiency [J]. Proceedings of the CSEE, 2013, 33(16): 1-8.

[2]张玲玲, 杨明玉, 梁武. 基于相似日和LS-SVM的微网短期负荷预测[J]. 电力建设, 2014, 35(11): 32-37. ZHANG Lingling, YANG Mingyu, LIANG Wu. Microgrid short-term load forecasting based on similar days and LS-SVM[J]. Electric Power Construction, 2014, 35(11): 32-37.

[3]杨丹萍, 叶林, 赵永宁, 等. 住宅直流微网供电技术研究现状[J]. 电力建设, 2014, 35(11): 25-31. YANG Danping，YE Lin，ZHAO Yongning，et al. Research status of residential DC microgrid power supply technology[J]. Electric Power Construction, 2014, 35(11): 25-31.

[4]石庆均, 耿光超, 江全元. 独立运行模式下的微网实时能量优化调度[J]. 中国电机工程学报, 2012, 32(16): 26-35. SHI Qingjun, GENG Guangchao, JIANG Quanyuan. Real-time optimal energy dispatch of standalone microgrid[J]. Proceedings of the CSEE, 2012, 32(16): 26-35.

[5]宁阳天, 李相俊, 麻秀范, 等. 基于改进粒子群算法的微网动态经济调度算法[J]. 电力建设, 2014, 35(6): 26-30. NING Yangtian, LI Xiangjun, MA Xiufan，et al. Microgrid dynamic economic dispatch based on improved particle swarm optimization[J]. Electric Power Construction, 2014, 35(6): 26-30.

[6]朱兰, 严正, 杨秀. 计及需求侧响应的微网综合资源规划方法[J]. 中国电机工程学报, 2014, 34(16): 2621-2628. ZHU Lan, YAN Zheng, YANG Xiu. Integrated resources planning in microgrid based on modeling demand response[J]. Proceedings of the CSEE, 2014, 34(16): 2621-2628.

[7]张磊, 杨洪明, 刘文询. 基于矩不确定分布鲁棒的微网经济调度[J]. 电力科学与技术学报, 2015, 30(2): 35-40. ZHANG Lei, YANG Hongming, LIU Wenxun. Microgrid economic dispatch based on distributionally robust of moment uncertainty[J]. Journal of Electric Power Science and Technology, 2015, 30(2): 35-40.

[8]彭春华，谢鹏，詹骥文, 等. 基于改进细菌觅食算法的微网鲁棒经济调度[J]. 电网技术, 2014, 38(9): 2392-2398. PENG Chunhua, XIE Peng, ZHAN Jiwen，et al. Robust economic dispatch of microgrid using improved bacterial foraging algorithm[J]. Power System Technology, 2014, 38(9): 2392-2398.

[9]Gupta R A, Gupta N K. A robust optimization based approach for microgrid operation in deregulated environment[J]. Energy Conversion and Management, 2015(93): 121-131.

[10]ALAVI S A, AHMADIAN A, ALIAKBAR-GOLKAR M. Optimal probabilistic energy management in a typical micro-grid based-on robust optimization and point estimate method[J]. Energy Conversion and Management, 2015(95): 314-325.

[11]曾鸣, 段金辉, 孙静惠. 基于改进和声搜索算法的微网电池储能系统规划模型[J]. 电力建设, 2015, 36(10): 27-33. ZENG Ming, DUAN Jinhui, SUN Jinghui. Battery energy storage system planning model of microgrid based on improved harmony search algorithm[J]. Electric Power Construction, 2015, 36(10): 27-33.

[12]肖峻, 张泽群, 张磐, 等. 用于优化微网联络线功率的混合储能容量优化方法[J]. 电力系统自动化, 2014, 38(12): 19-26. XIAO Jun, ZHANG Zejun, ZHANG Pan，et al. A capacity optimization method of hybrid energy storage system for optimizing tie-line power in microgrids[J]. Automation of Electric Power Systems, 2014, 38(12): 19-26.

[13]ZUGNO M, CONEJO A J. A robust optimization approach to energy and reserve dispatch in electricity markets[J]. European Journal of Operational Research，2015, 247(2):659-671.

[14]孙建龙, 吴锁平, 陈燕超, 等. 基于改进NSGA2算法的配电网分布式电源优化配置[J]. 电力建设, 2014, 35(2):86-90. SUN Jianlong, WU Suoping, CHEN Yanchao. Optimal configuration of distributed generation in distribution network based on improved NSGA2[J]. Electric Power Construction, 2014, 35(2):86-90.

[15]DHEER D K, SONI N, DOOLLA S. Improvement of small signal stability margin and transient response in inverter-dominated microgrids[J]. Sustainable Energy Grids & Networks, 2016(5): 135-147.

(编辑 张媛媛)

Robust Optimization Planning Model for Microgrid System

ZENG Ming1, YANG Yongqi1，FAN Shiyuan1，Sun Chenjun2

(1. School of Economics and Management, North China Electric Power University, Beijing 102206, China; 2. State Grid Hebei Electric Power Company, Shijiazhuang 050000, Hebei Province, China)

The uncertainty of distributed renewable energy generation has brought serious negative influence on the optimization planning of microgrid system. This paper studies the robustness constraints based on the deviation between real deviation and estimated deviation of distributed generation, constructs the robust optimization model with system planning cost and operation cost as objective function, and proposes related NSGA-II optimization algorithm. At last, the example analysis results show that the proposed robust optimization model can get the optimal system planning scheme under the certain conditions of robust constraints and system operation constraints, which can provide decision basis for the robust optimization planning of microgrid system.

microgrid; robust optimization; distributed generation; NSGA-II algorithm

国家自然科学基金项目(71271082)；中央高校基本科研业务费专项资金资助项目(2015XS43)；国家电网公司科技项目(分布式电源发展适用性策略分析及评估研究)

TM 715

A

1000-7229(2016)07-0020-07

10.3969/j.issn.1000-7229.2016.07.003

2016-01-31

曾鸣(1957)，男，教授，博士生导师，主要研究方向为能源互联网、电力系统规划；

杨雍琦(1990)，男，博士研究生，本文通信作者，主要研究方向为电力技术经济、电力系统规划。

Project supported by National Natural Science Foundation of China(71271082)；Fundamental Research Funds for the Central Universities(2015XS43)