交叉布索预应力立体桁架拱静力与稳定性研究

贺拥军，张相扬，周绪红，2

(1.湖南大学 土木工程学院，湖南 长沙 410082；2.重庆大学 土木工程学院，重庆 410044)

交叉布索预应力立体桁架拱静力与稳定性研究

贺拥军1，张相扬1，周绪红1，2

(1.湖南大学 土木工程学院，湖南 长沙 410082；2.重庆大学 土木工程学院，重庆 410044)

为提高拱结构的承载力与刚度，改善其静力性能，根据张弦梁结构的布索特点，提出一种新型索拱结构。选取桁架拱为研究对象，建立跨度为100 m的交叉布索预应力桁架拱结构和普通桁架拱结构模型，采用ANSYS分析不同矢跨比下各布索方案结构的最大竖向位移、支座水平反力、杆件内力峰值和内力分布情况、在全跨和半跨荷载作用下的静力稳定性、屈曲模态，以及拉索节点位置对其稳定性能的影响。研究结果表明:索杆体系的引入能有效改善纯拱的受力性能，提高结构的极限承载力和刚度；在全跨、半跨荷载作用下，本文建议的结构最优矢跨比均为0.3；拉索节点位置对结构极限承载力有很大影响。关键词：交叉布索；桁架拱；静力性能；稳定性；极限承载力

钢拱结构具有良好的力学性能，在桥梁、体育场馆、会展以及交通枢纽等大跨度和超大跨度建筑中得到了广泛应用，其主要结构形式有实腹式钢拱、格构式钢拱和索拱结构三大类[1]。近十几年来，国内外学者在索拱结构形式的创新以及稳定性能的研究方面取得了丰硕的成果[2-9]。郭彦林等[2]对车辐拱结构平面内弹性稳定性进行了研究，指出其稳定性能比纯拱结构有很大改善，提出了车辐结构适用的矢跨比和高度的变化范围。杨大彬等[3]提出了一种新型落地索拱结构，相比于其他类型索拱结构，该结构可以保持较高室内净空，建筑使用功能和建筑效果较好。贺拥军等[4]针对折线型立体桁架拱结构，提出了4种拱平面内的布索方案,研究了4种方案下预应力拱结构的静力及稳定性能。黄利锋等[5]采用考虑双重非线性的有限元方法对内凹式索拱结构的极限承载力进行了参数研究与拱结构相比，该结构的整体稳定性、极限承载力、整体刚度都大幅度提高。目前，针对实腹式拱结构的布索方案研究、受力特性分析及结构优化设计，已有很多文献[2-3,5-9]研究，而对于格构式钢拱结构的力学特性分析则较少。为进一步提高立体桁架拱结构承载力与刚度，改善其受力性能，本文选择立体桁架拱(以下简称纯拱)结构为模型进行研究。

1 桁架拱布索方案分析

图1为几种常用的索拱方案。针对桁架拱结构，根据张弦梁布索的特点，提出一种交叉布索桁架拱结构。本索拱结构相对于张弦梁结构可以有效提高其净空使用面积，相对于只布置拉索的拱结构，可以更大幅度提高纯拱结构在全跨、半跨荷载作用下的刚度及承载力。

图1 现有索拱结构方案Fig.1 Existing cable arch scheme

张弦梁结构是目前较成熟的一种杂交结构，由上弦刚性压弯构件与下弦柔性拉索组合，通过合理地布置撑杆形式而形成的一种自平衡结构体系，充分发挥刚性、柔性材料的受力特性，更合理、经济地增大结构跨度[10-13]。但是张弦梁结构在梁下布置撑杆和拉索，梁结构的净空减小。本文根据张弦梁结构布索特点提出交叉布索预应力立体桁架拱(以下简称索拱)。布索方案如图2(其中粗实线表示撑杆，细实线表示拉索)。图2(a)所示为纯拱结构，图2(b)所示的布索方案，是由2个类似张弦梁结构的布索方式在拱结构顶部交叉布置而成。通过研究发现，将拉索在A点连接在一起，对受力性能改善效果更好。同时，将中部两根撑杆连接在A点，形成最终的布索方式。拉索端点B和C的位置可以根据工程实际需要进行设计。方案2是将方案1中的撑杆只保留中间2根，两侧撑杆去掉。方案3是将方案2中与支座相连的2根索去掉，只保留上部的索杆。

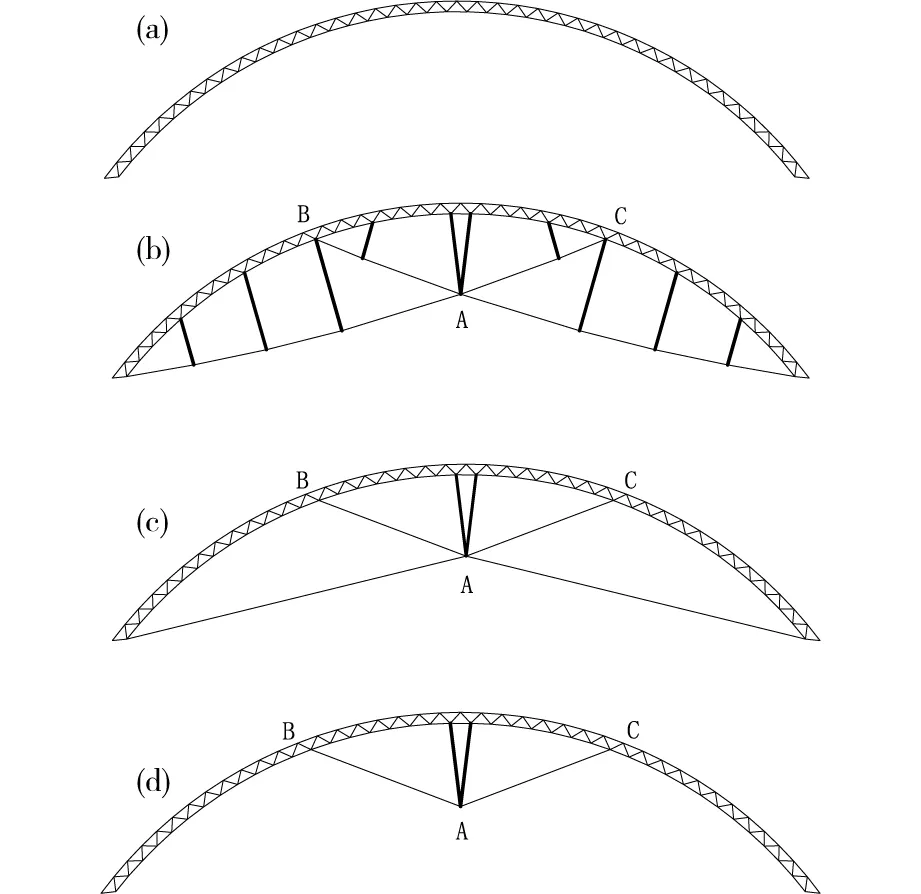
(a)纯拱结构;(b)方案1;(c)方案2;(d)方案3图2 交叉型索拱结构布索方案Fig.2 Schemes of crosscable arch

2 静力性能分析

2.1 结构计算模型及分析方法

选取工程上常用的倒三角桁架拱为研究对象，针对3种布索方案选用跨度为100 m, 矢跨比分别取为0.1，0.15，0.2，0.25，0.3，0.35和0.4的桁架拱，拉索的垂跨比选为0.031 25，上、下弦杆的截面选用Φ236×12，腹杆的截面选用Φ130×5。选用桁架拱截面高度1.5 m,截面宽度1.5 m，拉索截面54×Φ7，撑杆选用Φ328×10，钢弹性模量为2.1×10×1011N/m2，拉索弹性模量为1.8×10×1011N/ m2。利用荷载等效原则，在桁架拱上弦所有上弦节点处同时作用22 kN的竖向集中力。拉索初始预应力均为100 MPa。

利用有限元法来研究索拱的受力性能，整个分析过程仅限于材料的弹性范围内，并假定拱结构只在平面内变形[4]。在桁架拱每个节点约束平面外的位移来考虑侧向支撑对结构的约束作用。选用ANSYS有限元软件，其中桁架拱弦杆采用BEAM188单元，腹杆、撑杆及拉索均采用LINK180单元模拟，各单元之间均假定为铰接。桁架拱两端的支承形式采用上下弦固定铰支。仅考虑结构几何非线性影响[14]。

2.2 静力性能分析与对比

在桁架拱结构中，矢跨比对结构受力性能的影响最明显。本节采用有限元分析法，先对不同矢跨比下桁架拱结构的最大节点位移降低情况进行研究，找出结构刚度随矢跨比的变化规律。然后对结构水平支反力和杆件内力分布这2个方面进行研究，对3种布索方案进行对比分析。

2.2.1 不同矢跨比下结构刚度的比较

对各方案索拱和纯拱结构进行静力性能分析，计算结果见表1。

表1 3种方案的索拱结构最大节点位移Table 1 Maximum nodal displacement of the structures

图3 不同矢跨比下各布索方案最大挠度降低率Fig.1 Decreasing rates of maximum deflection of structures with different rise-span ratios

由表1可以看出：随着矢跨比增大，索拱结构与纯拱结构的竖向位移都呈现减小趋势。3种方案结构的最大节点竖向位移均明显小于纯拱结构。由图3可以发现，随着矢跨比增大，结构最大竖向位移降幅也不断增大，表明索拱结构对于大矢跨比结构的刚度改善效果更明显。针对提高结构刚度而言，方案3略优于方案1和方案2，方案1和方案2效果相差不大。实际上，由于桁架拱结构的最大竖向位移主要由桁架拱顶部的刚度决定，顶部的索杆体系提高了结构的局部刚度，故3种方案索拱结构最大节点竖向位移较纯拱结构减小。又由于方案1和方案2中存在与支座相连的预应力拉索，该预应力拉索给拱的中部一个向下的合力，从而加大了2种方案结构的最大节点位移。

2.2.2 不同矢跨比下支座水平反力比较

拱结构支座处有很大的水平推力，判断布索方案的是否合理，还需要考虑支座水平反力的减小幅度。所以本节从水平支反力方面分析各布索方案的特点。

保持其他几何条件和荷载情况不变，本节针对不同矢跨比各方案结构进行静力分析。支座反力计算结果如表2所示，结构水平支座反力降低率见图4。

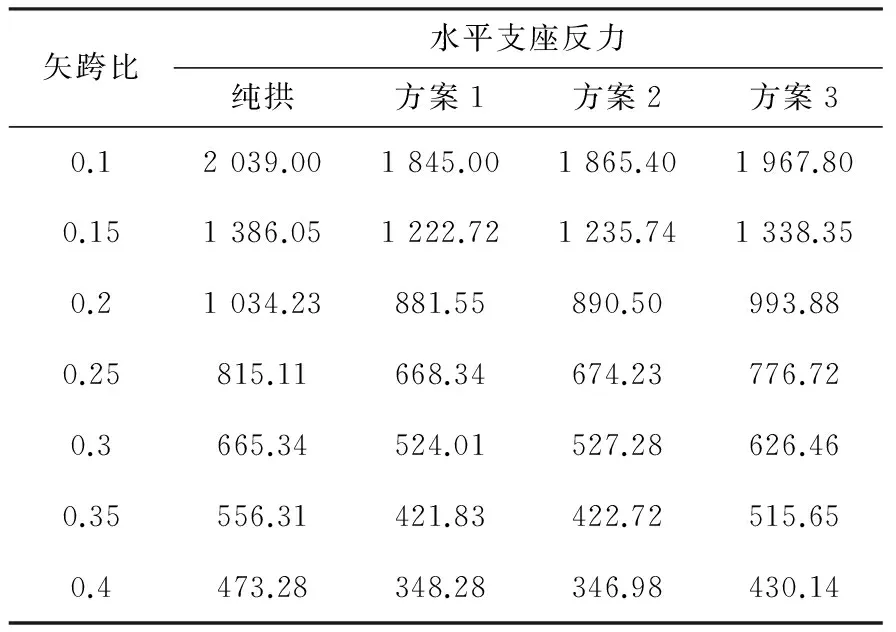
表2 3种布索方案下结构的支座反力对照表Table 2 Bearing reactions of structures with three schemes

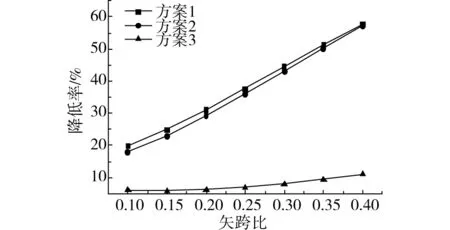
图4 不同矢跨比下各方案支座反力降低率Fig.4 Decreasing rates of bearing reactions of structures with different rise-span ratios of three schemes

由表2和图4可以发现，在初始预应力为100 MPa时，3种方案水平支反力都随着矢跨比的增大而减小。方案1和方案2支座反力的降低幅度明显大于方案3。除矢跨比为0.1的情况下，降低幅度都在10%以上，降低率随着矢跨比的增大变化很大，在矢跨比为0.4时达到最大值为57.8%。而方案3支座反力降低率均在10%以下，改善效果不明显。实际上，因为方案3没有布置与支座相连的拉索，故支座反力减小不明显。而方案1与方案2相比，方案1中，由于两侧布置撑杆，使拉索与水平方向夹角减小，在预应力相同的情况下，拉索在水平方向上的分力较方案2大，因此支座反力降低幅度更多。

综合可见，方案1和方案2可以有效降低支座反力，效果基本相同，而方案3效果较差。

2.2.3 杆件内力分析

从预应力自平衡体系概念出发，除非结构的预应力与荷载作用系统完全吻合，否则在结构体系内总会产生杆件的卸载效应与增载效应，即某些杆件因预应力卸载的同时伴随着另一些杆件的增载[4]。因此本节对矢跨比为0.25时索拱与纯拱进行杆件内力分布情况进行对比分析。考虑到结构及荷载分布的对称性，此处绘出1/2拱范围内结构杆件内力的分布情况，如图5(b)和5(c)所示，其中轴力负值表示杆件受压，杆件编号见图5(a)。

由图5分析可得：预应力索杆体系改变了结构的内力分布情况。对于上弦杆，方案1，2和3杆件内力幅值分别降低12.0%，13.5%和20.6%。在纯拱结构中，上弦杆件内力分布为：由支座至拱顶先减小再增大，幅值出现在支座处。布索后上弦杆件内力分布变为：由支座至拱顶先增大再减小，之后再增大，在拉索上节点C附近达到最大值，这说明拉索增大了节点C附近杆件的内力，减小了支座和拱顶处杆件的内力。对于下弦杆，杆件内力幅值降低不明显。下弦杆件内力分布变化规律与上弦杆件相反，纯拱结构下弦杆件内力分布为由支座至拱顶先增大再减小，在86号杆达到最大值，而布索结构下弦杆件内力分布变为：由支座至拱顶的先减小再增大，幅值出现在支座附近。总体而言，索杆的布置，使桁架拱中间顶部内力很小的下弦杆件内力增大，中间顶部内力比较大上弦杆件内力减小，使结构杆件内力分布更加均匀，材料利用更加充分，同时也减小了杆件内力幅值。

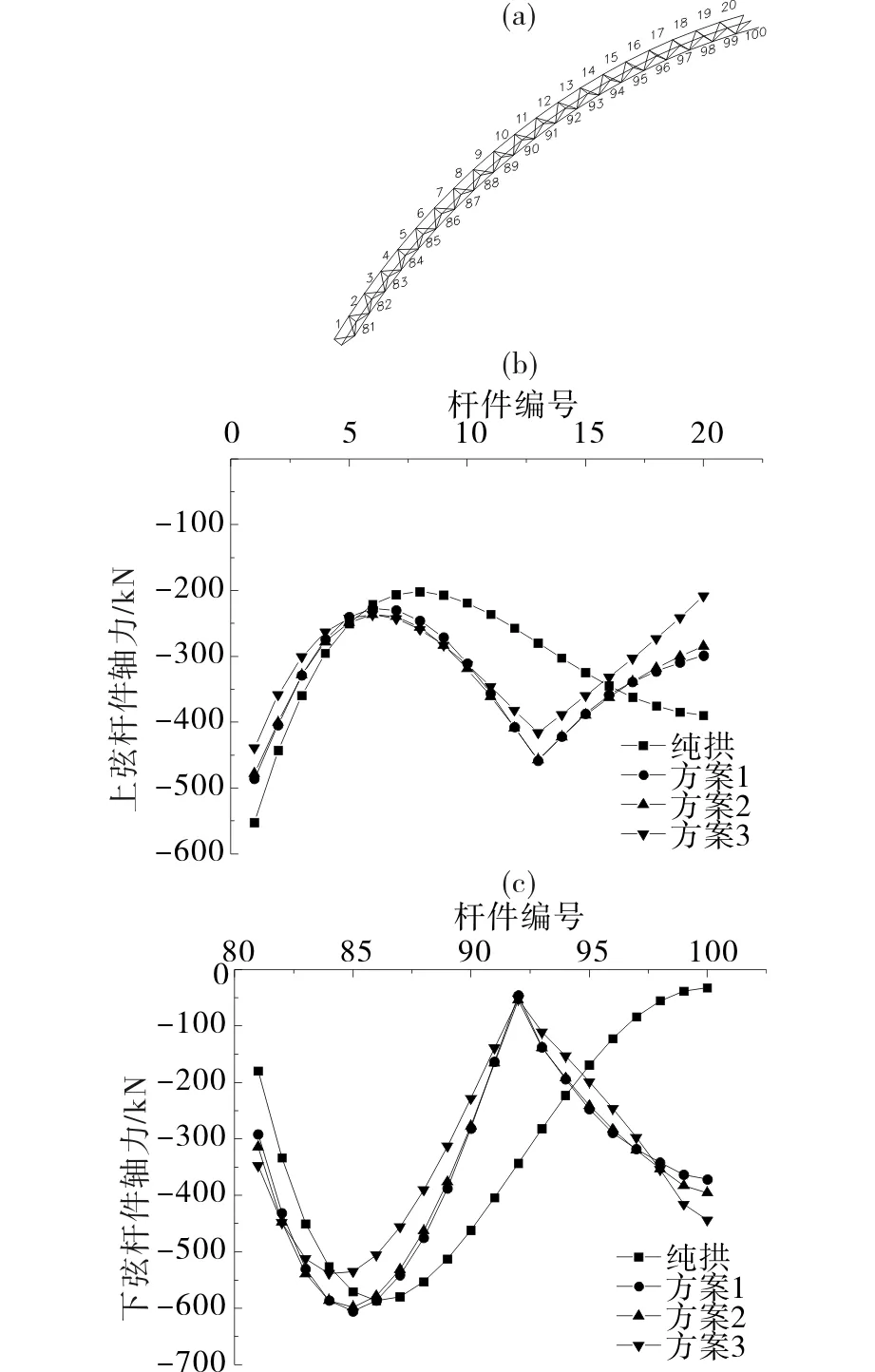
(a)杆件编号；(b)上弦杆件内力分布；(c)下弦杆件内力分布图5 杆件编号及内力分布Fig.5 Distribution of internal forces of structures

3 整体稳定性能分析

一般情况下，平面外的稳定性可以通过设置足够的面外支撑来保证[15]，因此，本节只研究结构的平面内稳定。本节对索拱结构和纯拱结构进行极限分析，得到其荷载-位移全过程曲线，分析结构刚度及承载力提高情况。

3.1 全跨荷载作用下索拱结构和纯拱结构稳定性分析

取矢跨比为0.1，0.15，0.2，0.25，0.3，0.35和0.4的索拱结构和纯拱结构，进行极限分析，得到其极限荷载(见表3)，图6为矢跨比为0.25时结构的荷载位移-曲线。

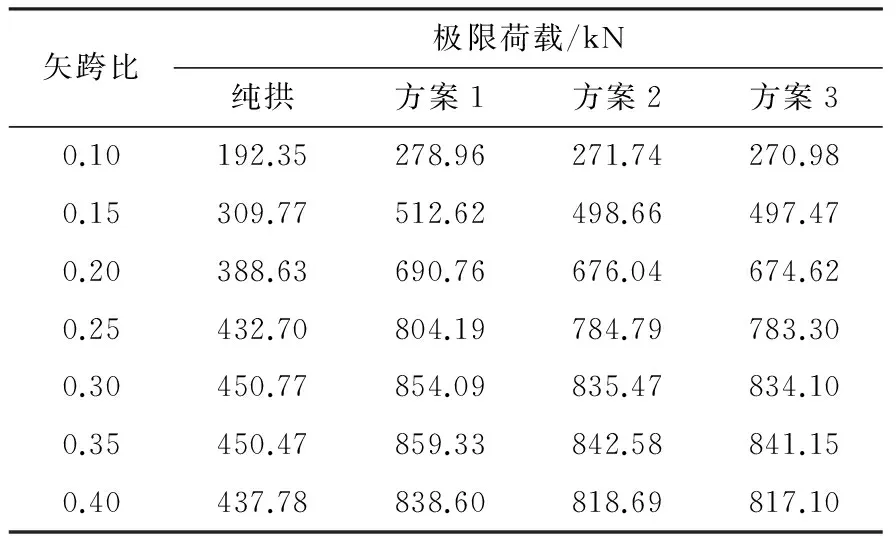
表3 结构极限荷载(全跨荷载)Table 3 Ultimate loads of structures(full span load)

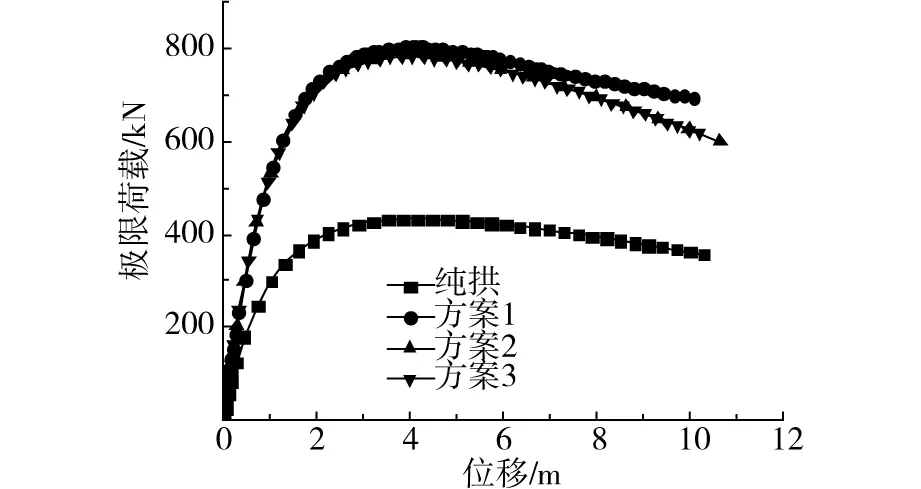
图6 全跨荷载作用下荷载-位移曲线Fig.6 Load-displacement curves of structures under full-span load

由表3可以发现，3种方案索拱的极限荷载较纯拱结构均有较大的提高，提高程度基本相当，且随着矢跨比增大，提高率也逐渐变大，在矢跨比为0.35时取得最大，最大提高了91%，说明各方案对大矢跨比拱的极限承载能力提高程度更明显。通过对比3种方案发现，在全跨荷载作用下，3种方案承载力的提高程度基本相同，这是因为位于拱顶部的索杆起主要作用，提高了跨中部分的刚度，而两侧的索杆起次要作用，对全跨荷载下承载力的提高作用不明显。

由图6可以看出，在相同的荷载下，3种方案索拱结构的位移相差不大，且均比纯拱结构小，说明索拱结构整体刚度相比纯拱结构有较大提高。3种方案索拱结构刚度相差不大，这是因为位于拱顶部的索杆起主要作用，提高了跨中部分的刚度。

3.2 半跨荷载作用下索拱结构和纯拱结构稳定性分析

文献[1]指出，拱形钢结构在全跨荷载作用下一般具有较高的刚度和承载力，但半跨荷载下则相对较低，因此设计中需重点考虑荷载不对称分布的情况[1]。仍以100 m跨度的索拱结构为例，绘制半跨荷载下的荷载-位移曲线,如图7所示,表4为其极限荷载。

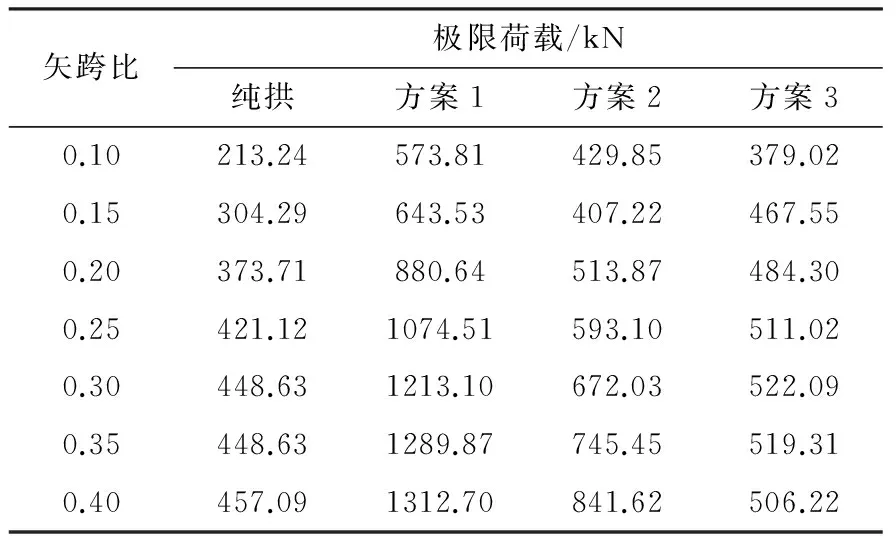
表4 结构极限荷载(半跨荷载)Table 4 Ultimate loads of structures(half-span load)

图7 半跨荷载作用下结构荷载-位移Fig.7 Load-displacement curves of structures under half-span load

表4表明：在半跨荷载作用下，3种索拱结构极限承载力与纯拱结构相比有不同程度的提高，方案1极限荷载提高率均在110%以上，在矢跨比为0.4时达到188%。由图7可以发现，半跨荷载作用下，方案1，2对结构的极限承载力和刚度提高效果比较明显，方案3基本没有提高。其中，方案1效果最明显，这主要是因为方案1结构中的受荷载作用的半跨索杆与桁架拱结构组成类似于一榀张弦梁的结构,对结构的变形起到了很好的约束作用，而未施加荷载的半跨的索杆此时起次要作用，而且在变形达到一定值时，未施加荷载半跨的索杆可能会退出工作。方案2结构由于没有两侧撑杆导致结构的刚度略有降低，承载力大幅度减小，是因为方案2结构失稳的部位没有撑杆，导致结构变形更大，结构过早出现失稳。方案3结构在达到极限荷载之前极限承载力和刚度提高不明显，但是在达到极限荷载之后，承载力仍可以缓慢增加，这是由于达到极限荷载之后，拱的侧向变形很大，此时拉索撑杆体系对结构的变形起到了限制作用。

综合分析，方案1结构静力和稳定性能最优，故下文分析方案1非线性屈曲模态和拉索节点位置对其稳定性能的影响。

3.3 非线性屈曲模态分析

计算分析表明，索拱结构与纯拱结构达到极限荷载后发生失稳，屈曲模态如图8所示，其中图8(a)和图8(b)分别为全跨、半跨荷载下纯拱结构与索拱结构失稳模态。

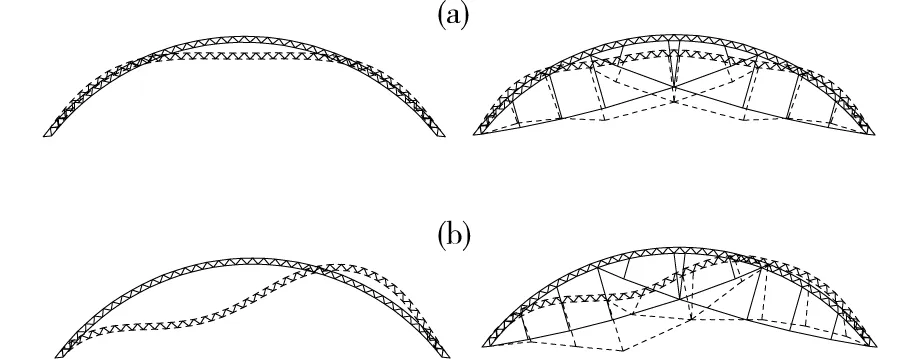
(a)全跨荷载失稳模态;(b)半跨荷载失稳模态图8 非线性屈曲模态Fig.8 Buckling modes of structures

由图8(a)可知，在全跨荷载作用下，索拱结构失稳时变形与纯拱结构相似，均为两边向外凸起，中部塌陷，但不同的是，索拱结构中部有一点上翘，中间部位的整体性更好，因此提高了极限承载力。由图8(b)可知，在半跨荷载作用下，索拱结构失稳与纯拱结构类似，均为非对称失稳，但是索拱结构的变形明显小于纯拱结构，由于有索杆的存在，受荷载作用半跨和非荷载作用半跨变形都有很大幅度减小，说明索杆体系能有效约束结构的变形，大幅度提高结构的极限承载力和刚度。

3.4 拉索节点位置变化对稳定性能的影响

保持其他条件不变，改变拉索与拱连接点B和C的位置，图9为矢跨比为0.25的结构模型图，图9(a)，图9(b)和图9(c)分别对应位置1，位置2和位置2。对索拱结构和纯拱结构进行弹性极限分析，得到相应的极限荷载(见表5～6)。

由表5～6可以看出，拉索节点位置对结构极限承载力有很大影响。由表5可以得出，在全跨荷载作用下，随着拉索节点B和C位置由拱顶向支座移动，极限承载力不断增加。实际上，由于中部索杆体系对提高全跨荷载作用下的承载力起主要作用，随着B和C点由拱顶向支座移动，中部索杆体系高度增大，故承载力大幅度增加。由表6可以得出，在半跨荷载作用下，随着B和C位置由拱顶向支座移动，极限荷载先增加后减小。在3种位置中，位置2时结构极限荷载最高，也就是说节点B和C的位置存在一个最优位置，大概在桁架拱的1/4跨度处。究其原因，在半跨荷载作用下，首先进入屈服的位置是约3/4 跨度处的下弦，继而是约1/4跨度处的上弦[15]，结构变形为反对称，变形最大的位置在结构的1/4处，故拉索节点B和C布置在此处，拉索限制了3/4跨度处水平位移的发展，同时，撑杆限制了1/4跨度处水平和竖向位移的发展，故结构的极限承载力最大。在全跨、半跨荷载作用下，随着矢跨比的增大，极限荷载不断增大，在矢跨比小于0.3时增长较快，矢跨比大于0.3之后增长缓慢，故本文建议的最优矢跨比为0.3。

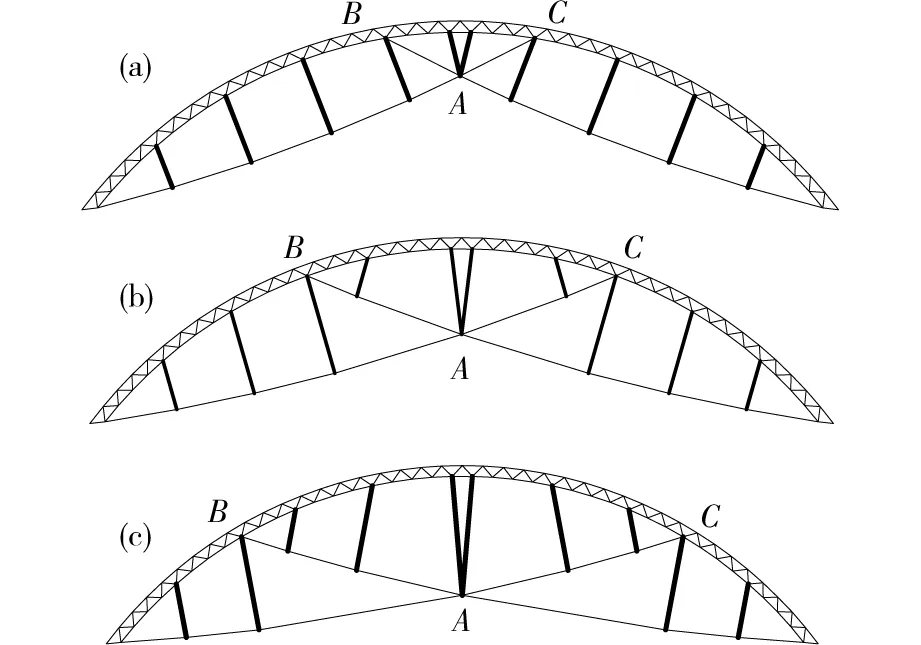
(a)位置1；(b)位置2；(c)位置3图9 不同拉索节点位置模型图Fig.9 Structure models with different cable joint positions

表5 不同拉索节点位置结构极限荷载(全跨荷载)Table 5 Ultimate loads of structures with different cable joint positions (full-span load)

表6 不同拉索节点位置结构极限荷载(半跨荷载)
Table 6 Ultimate loads of structures with different cable joint positions (half-span load)

矢跨比极限荷载/kN纯拱位置1位置2位置30.10213.24290.57573.81352.600.15304.29469.22643.53578.150.20373.71631.28880.64674.990.25421.12780.321074.51808.450.30448.63836.691213.10846.340.35459.29865.901289.87881.040.40457.09875.671312.70916.20

4 结论

1)本文提出的索拱结构较纯拱结构刚度提高效果显著，方案1和方案2可以有效降低支座反力，效果基本相同，而方案3效果较差，索杆体系使结构杆件内力分布更加均匀，减小了杆件内力幅值。

2)在全跨、半跨荷载作用下，索拱结构的极限荷载较纯拱结构有较大提高，且随着矢跨比增大，提高率也逐渐变大，索拱结构对大矢跨比结构的极限承载能力改善程度更明显，本文建议的最优矢跨比为0.3。

3)在半跨荷载作用下，索拱结构极限承载力和刚度与纯拱结构相比有不同程度的提高，只有加载半跨的索杆起到控制结构变形的作用，而非加载半跨的索可能会发生松弛现象。

4)拉索节点位置对结构极限承载力有很大影响。全跨荷载作用下，随着拉索节点位置由拱顶向支座移动，极限承载力不断增加。半跨荷载作用下，随着拉索节点位置由拱顶向支座移动，极限承载力先增大后减小，在拱1/4跨度处达到最大值。

[1] 郭彦林,窦超.钢拱结构设计理论与我国钢拱结构技术规程[J].钢结构,2009,24(5):59-70. GUO Yanlin,DOU Chao. Design theory and Chinese technical specification for steel arch structure [J]. Steel Construction, 2009, 24(5):59-70.

[2] 郭彦林,王高宁.车辐结构平面内弹性稳定承载力及设计建议[J]. 空间结构,2006,12(1):18-23. GUO Yanlin, WANG Gaoning. In-plane elastic stability of spoke structures [J]. Spatial Structures,2006,12(1):18-23.

[3] 杨大彬,张毅刚,吴金志.新型落地索拱结构及其力学性能分析[J]. 建筑结构学报,2011,32(8):51-58. YANG Dabin, ZHANG Yigang, WU Jinzhi. New ground-supported cable arch structure and analysis of its mech-anical performance[J].Journal of Building Structures,2011,32(8):51-58.

[4] 贺拥军,章小桐,周绪红.拉索预应力折线型立体桁架拱布索方案研究[J].湖南大学学报(自然科学版),2011,38(8):7-12. HE Yongjun, ZHANG Xiaotong, ZHOU Xuhong. Resear-ch on arrangement styles of cables for pretensioned fol-ded line type 3D-trussed arch [J]. Journal of Hunan University (Natural Science),2011,38(8):7-12.

[5] 黄利锋,冯健,赵建,等.内凹式索拱结构极限承载力研究[J].建筑结构学报,2010,31(2):41-47. HUANG Lifeng, FENG Jian, ZHAO Jian, et al. Ultimate loading capacity of innerconcave cable arch st-ructure[J]. Journal of Building Structures, 2010,31(2):41-47.

[6] 郭彦林,胡淑辉.一种新型预应力索-拱结构的弹性稳定性能研究[J]. 空间结构,2005,11(3):33-38. GUO Yanlin, HU Shuhui. Elastic stability behavior of a new type of pre-stress cable-arch structure [J].2005,11(3):33-38.

[7] Wu M, Sasaki M. Structural behaviors of an arch stiffened by cables [J].Engineering Structures, 2007, 29(4) : 529-541． [8] Kang H J, Zhao Y Y, Zhu H P, et al. Static behavior of a new type of cable-arch bridge [J].Original Research Article Journal of Constructional Steel Research, 2013,81(2):1-10.

[9] 蒋友宝,廖国宇. 全跨荷载作用下内凹式索拱结构受力过程中刚度的变化[J]. 工业建筑,2014(11):150-154. JIANG Youbao, LIAO Guoyu. Stiffness changes in loading process for inner concave cable-arch structure under full-span load [J]. Industrial Construction,2014,44(11):150-154.

[10] He Y J, Sun S, Zhou X H. The elastic static property and stability of string cylindrical reticulated mega-structures [J]. Journal of Constructional Steel Research, 2015, 11(4):20-29.

[11] Han Q H , Xu Y, Lu Y, et al. Failure mechanism of steel arch trusses: Shaking table testing and FEM analysis [J].Engineering Structures, 2013, 82(1): 186-198.

[12] Makowski Z S. Space structures of today and tomorrow [C]// Third International Conference on Space Structures. London: Elsevier Applied Science Publishers Ltd, 1984:1-8.

[13] Saitoh M, Okasa A. The role of string in hybrid string structure [J]. Engineering Structures, 1999, 21(8):756-769.

[14] 白正仙,刘锡良.张弦梁膜结构几何非线性分析[J].北京工业大学学报, 2002,28(1):22-25. BAI Zhengxian, LIU Xiliang. Geometrically nonlinear analysis on the beam string structure composed of membrane[J]. Journal of Beijing Polytechnic University, 2002,28(1):22-25.

[15] 郭彦林,郭宇飞,窦超.钢管桁架拱平面内失稳与破坏机理的数值研究[J]. 工程力学,2010,27(11):46-55,63. GUO Yanlin , GUO Yufei, DOU Chao. Numerical study on stability behavior and failure mechanism of steel tube truss-arches[J]. Engineer Mechanics,2010,27(11):46-55,63.

Research on the static and stability behavior of cross cable pre-stressed 3D-truss arch

HE Yongjun1, ZHANG Xiangyang1, ZHOU Xuhong1,2

(1.College of Civil Engineering, Hunan University, Changsha 410082, China;2.College of Civil Engineeting, Chongqing University, Chongqing 410044, China)

In order to improve the bearing capacity and rigidity of the pure arch structure, a new cable arch structure is proposed based on the concept of the beam string structure. Ordinary arch and cable arch models with span of 100m are built. The maximum deflection, horizontal support reaction, peak value of member internal force and distribution of internal force, ultimate load and buckling mode of the structure, and the influence of the position of cable joints are analyzed with utilizing ANSYS. The result shows that, the adoption of the prestressing system can significantly improve the stress state of the truss arch, along with the rigidity and ultimate bearing capacity of the structure. And the optimal ratio is 0.3 under full-span load and half-span load. The position of the cable joints has great influence on the ultimate bearing capacity of the structure.

cross cable; truss arch; static performance; structural stability; ultimate bearing capacity

2015-11-19

国家重点研发计划项目(2016YFC0701201)；湖南省高校科技创新团队滚动资助计划项目(湘财教指(2015)616号)

贺拥军(1970-)，男，湖南宁乡人，教授，博士，从事钢结构及大跨空间结构理论与应用研究；E-mail:hyj0087@163.com

TU393.3

A

1672-7029(2016)12-2420-07