基于不同数据处理方法的击实特性求解及应用

赵 敏， 厉广广， 尹文静

(西安工业大学 建筑工程学院， 陕西 西安 710032)

基于不同数据处理方法的击实特性求解及应用

赵 敏， 厉广广， 尹文静

(西安工业大学 建筑工程学院， 陕西 西安 710032)

结合土工击实试验相关规程，以江苏某省道改扩建工程路基土随机取样试验数据为依托，对两种击实最佳指标求解方法进行对比分析，应用二次曲线拟合法对不同灰剂量、不同制备方法和不同击实方式混合料击实指标进行求解。结果表明：路基土的最佳击实指标求解宜采用三点二次插值法或二次曲线拟合法，曲线拟合次数不宜过高，否则容易导致最大干密度虚假偏大，压实度偏小，影响道路压实效果；改变土样的石灰剂量，由0增大至8%，最优含水率呈二次曲线递减，最大干密度呈三次曲线递增；击实土重复利用所测最大干密度比原状土大，最优含水率比原状土小；与轻型击实相比，重型击实的最大干密度要大得多，而最佳含水率要小得多。

击实曲线； 拟合； 最大干密度； 数据插值； 最优含水率

压实度是保证路基强度和稳定性的直接因素之一，在外力作用下，路基压实土干密度增加从而改变其压实度[1]，工程中通常以室内标准击实试验曲线来确定土的最大干密度，以之作为衡量压实性的重要指标。目前关于土的标准击实试验理论和计算方法已相对成熟，主要包括数解法(数据差值)和图解法(曲线拟合)两种。文献[2，3]对击实试验的试验方法进行介绍，并研究了最大干密度和最优含水率两个击实指标的关系，分析其准确性；冯忠居[4]通过三点二次插值法的数值解析方法对最佳压实指标进行分析求解；文献[5，6]和[7，8]分别借助Excel和Matlab软件生成ω-ρ曲线，通过图解法求得最佳压实指标，在工程中得到了广泛应用；而文献[9，10]则通过实验分析和理论计算对传统最佳击实指标求解方法进行优化和改进，使得数据结果更加精确，更贴合实际。

现行土工击实试验规程对于最大干密度和最佳含水率的取值均采用作图取峰值点的方法，但土工试验规程[11]采用的是实际击实曲线，而无机结合料稳定材料试验规程[12]采用的是二次拟合曲线。针对这一差异，本文在总结前人研究成果的基础上对两种击实指标求解方法进行对比，验证试验规程对于最佳压实指标求法的可靠性，并运用在具体案例中，研究石灰剂量、土样制备、击实方式等对击实指标的影响，以指导工程实际。

1 两种求解方法

数据插值和曲线拟合是常用的两种数据处理方法，均能较好地将离散点按照某一趋势生成连续函数，通过"窥几斑"实现"知全豹"的目的[13]。二者的主要区别在于是否要求连续函数曲线过已知离散点，插值函数在离散点上要求满足约束，而拟合则是要求误差总量最小，最大限度逼近离散点。本文随机选取江苏某省道改扩建工程S1标段某取土坑土样的标准击实试验为研究对象，采用轻型击实方式进行击实，下图为5%石灰土标准击实试验最大干密度和最佳含水率成果表。

表1 标准击实试验最大干密度和最佳含水率成果

1.1 数据插值

互不相等的n+1组数据(离散点或称插值节点)(xi,yi)，可以得到一个确定的n次插值函数，P(xi)=yi(i=0，1，2，3，…，n)，即对于表1数据，最高可以确定一个4次插值多项式。一般地，n次插值多项式可表示为[14]：

基函数为：

式中：ω和ρ分别为含水率和干密度。易求得，其一阶导数为零时：最优含水率ωo=18.6，最大干密度ρmax=1.59，即利用三点二次插值法求得该试验工况下最优含水率为18.6%，最大干密度为1.59 g/cm3。

1.2 曲线拟合

已知平面上n组数据(xi,yi)(i=0，1，2，3，…，n)，通过曲线拟合可以寻求在某种准则下所有数据点无限逼近的函数(拟合曲线)y=f(x)，逼近程度越高，则曲线的拟合优度(Goodness of Fit)越好，可决系数R2的值越接近1。

参照文献[6]中Excel拟合击实试验标准曲线的方法，对表1中的5组数据进行不同次数的多项式拟合，得到如图1所示的拟合曲线和最佳击实指标。

对拟合曲线方程求最值，高次方程采用Newton迭代法[16]求其一阶导数的零点，求得不同次数拟合曲线峰值点汇总如表2所示。

图1 击实试验拟合曲线

计算成果曲线次数23≥4拟合曲线方程y=-0.0033x2+0.125x+0.48376y=1.5×10-4×x3-0.01193x2+0.28301x-0.47068y=3.6×10-4×x4-0.0265x3+0.72789-8.7268x+40.627可决系数R20.905110.912791图解法(ωo,ρmax)(18.6%,1.66)(18.6%,1.67)(18.6%,1.67)Newton迭代法(ωo,ρmax)(18.8%,1.66)(17.9%,1.63)(14.2%,1.73)

1.3 对比分析

由图2可知，标准击实试验离散数据整体满足n次多项式函数，且n越高其数据点在曲线周围分布越均匀，曲线拟合度越高。其中当n=2、3时曲线为光滑的“凸”字形，而当n≥4时，曲线两端出现上翘现象呈“Ω”型，不符合实际发展情况；由表2可知，拟合曲线次数越高，R2越接近1，由于精确度有限，图解最优含水率均保持在18.6%左右，而最大干密度随拟合次数增大而增加；使用Newton迭代法对拟合曲线方程最值进行求解，随着拟合曲线多项式次数(阶数)增加，混合料的最优含水率下降，最大干密度先减小后增大。对比图解法所得最佳击实指标，不难发现，次数越高这种差距越大，即在有限精度下拟合次数越高反而误差越大；对比数解法二次插值函数最值(ωo=18.6%，ρmax=1.59 g/cm3)，图解法所求最佳含水率与之一致，均为18.6%左右，而最大干密度则相对偏大，且拟合曲线次数越高其与数解法计算结果差值越大。

由压实度定义[12]可知土的最大干密度越大，压实度越大，即当拟合曲线次数较高时，压实度往往比实际虚假偏大，会造成因实际压实度达不到压实标准或配合比设计水泥用量人为减少等原因而引起路基强度不足、路面病害等不良后果。因此，标注击实曲线拟合次数不宜过高，二次多项式拟合曲线的拟合结果和三点二次插值法求解结果相差较小，二者相互验证，能够较为可靠地反映土的最优含水率和最大干密度，即试验规程中对最佳击实指标求解采用二次多项式拟合曲线或二次插值法是较为合理的。

2 工程应用

2.1 工程概况

该省道位于华南地台扬子准地台苏北坳陷，黄泛冲积平原为所处地区的主要地貌，局部为构造剥蚀丘陵，地势平坦，降水为其地下水补给的主要形式，沿线地层表面主要为第四系全新亚粘土、淤泥亚粘土，其中以可塑性较高的褐黄色、灰黄色亚粘性土为主，局部为不均匀亚砂土，基底主要为泥岩、砂岩。改扩建工程S1标合同段长约6.5 km，起迄桩号为K0+000～K6+500。该路段土质均匀，通过现场试验检测发现其击实特性等较为相似，随机选取某一取土坑土样作为试验研究的取样点，应用二次拟合曲线图解法研究灰剂量、土样制备方法、击实方式等不同因素对该取土土样最佳击实指标的影响，从而以样本特性反映该路段的整体特性，为类似工程提供参考。

2.2 灰剂量

选取剂量分别为0、3%、5%、6%、8%的石灰改善土土样进行标准击实试验，以图解法采用二次多项式拟合曲线对不同灰剂量最佳击实指标进行求解，如图2所示，得到不同灰剂量混合料的最优含水率和最大干密度绘制如图3所示灰剂量与干密度和含水率标准击实曲线变化图。

图2 不同灰剂量击实试验计算曲线

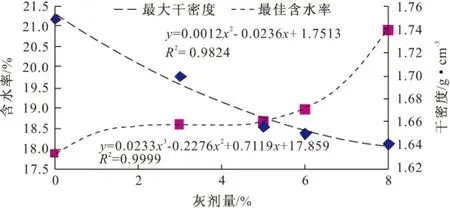
图3 灰剂量与干密度和含水率标准击实曲线

由图2可知，二次多项拟合曲线能够较好地反映ω-ρ变化规律，随着灰剂量增加，拟合曲线在坐标轴内整体呈向右下方移动的趋势，尤其是峰点位置变化最为明显，结合图3的拟合结果，不难发现最优含水率随灰剂量增加而增大，且呈三次曲线增长；而最大干密度随灰剂量增加而减小，呈二次曲线递减，此时相应的曲线拟合度较高，具有一般规律性。究其原因，一方面石灰掺入土体填充了土颗粒之间的空隙使得混合料级配更加均匀[17]，压实相对困难，石灰自身密度相对土体较小，掺入石灰剂量越多则混合料总体干密度越小，故最大干密度随灰剂量增加而减小；另一方面石灰中游离态分子与土体发生一定的物理化学反映，吸收土体中的自由水形成结晶体[18]，导致混合料水分在击实过程中损失减少，含水率增大。

2.3 土样制备方法

考虑到实际工程中，路基土会采用不同利用程度的回填土[19]，以及送检土样用量不足的突发情况，以土样是否重复利用为出发点，仍采用轻型击实对原击实素土配以5%灰剂量进行试验，采用二次曲线拟合法求解结果如图4。

图4 不同利用情况最佳击实曲线

由图4可知，相对原取土，重复利用的土样其最优含水率相对减小，简单计算不难得出减小了3.76%，最大干密度相对增大了0.48%，即土样是否重复利用主要影响混合料的最优含水率，对最大干密度影响相对较小，这主要是因为击实后的土颗粒物理性质发生了变化，超小直径细粒土过筛率下降，颗粒整体较未击实前偏大，土体易于压实，土中自由水在初次击实发生损失以及二次击实前存在一定程度上的蒸发现象。因此，为了保证击实指标的可靠性，在试验中不建议对土样进行重复利用。

2.4 击实方式

在实际工程中，路基压实效果受碾压机械、碾压方式、碾压遍数、碾压速度等多重因素影响[20]，目前常用击实试验方法根据击实功的大小主要分为重型击实、轻型击实试验法。本工程中分别采用单位体积击实功为2687 kJ/m3和598.2 kJ/m3的重型和轻型击实方式对5%灰剂量混合料进行击实，得到结果如图5所示。

图5 不同击实方式最佳击实曲线

由图可知，重型击实和轻型击实两种不同击实方法所得击实指标差异较大，相比轻型击实，重型击实最大干密度增大17.96%，最优含水率减小26.34%，即击实功对混合料最佳击实指标影响较大。在实际操作中要根据土颗粒粒径[11]等因素选取合适的击实方式。

3 结 论

对比曲线拟合法与数据插值法求得最佳击实指标结果，研究不同灰剂量、土样是否重复利用、击实方式等不同因素的击实特征，得出以下结论：

(1)三点二次插值数解法和二次曲线拟合图解法均能较好地反映最佳击实指标的变化情况，两种击实试验规程相互验证，在工程中具有较为广泛的应用价值。对于曲线拟合法，随着拟合次数(拟合多项式阶数)增加，离散点分布相对趋于均匀。二次、三次拟合曲线呈“凸”字形；四次及以上则拟合过度，呈“Ω”型，且高次拟合曲线求得最佳击实指标相对偏大，不能真实地反映路基压实度，为保证数据可靠性和计算操作方便性，一般取二次拟合曲线对最佳击实指标进行求解。

(2)以二次拟合曲线法求解不同灰剂量最佳击实指标，随着灰剂量增加混合料的最佳含水率大体呈二次曲线递减，而最大干密度大体呈三次曲线增长。

(3)二次击实混合料的最大干密度增大，最优含水率减小，对最佳击实指标影响明显，实际操作不宜对击实土进行重复利用。

(4)不同击实方式对混合料击实特性影响较大，重型击实比轻型击实所得最大干密度要大得多，最优含水率小得多。

[1] 王智超, 金 刚, 邓旭华, 等. 路基压实土的超固结应力历史试验研究[J]. 公路交通科技, 2015, 32(7): 41-46.

[2] 曹仕娟. 公路路基土室内击实试验研究[J]. 交通标准化, 2013,(22): 50-52.

[3] 张志权, 王志勇. 最大干密度和最优含水率的准确性探讨[J]. 长安大学学报(建筑与环境科学版), 2004, 21(2): 7-10.

[4] 冯忠居, 张永清. 粗粒土路基的压实试验[J]. 长安大学学报(自然科学版), 2004, 24(3): 9-12.

[5] 黄 英, 符必昌. 确定土的最大干密度和最优含水率的数解法[J]. 岩土工程学报, 2002, 24(4): 538-540.

[6] 田志峰, 张 波. 击实试验数据的Excel处理方法[J]. 科技促进发展, 2011, (s1): 109-112.

[7] 张向东, 周新勍, 张 玉, 等.辽西风积土多因素耦合击实试验[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(11): 1492-1496.

[8] 白宏光. 基于MATLAB的土工击实试验数据处理的探讨[J]. 交通科技, 2014, (6): 113-116.

[9] 周志军, 袁卓亚, 赵小兵. 土石混合料最大干密度理论计算方法研究[J]. 路基工程, 2007, (4): 18-19.

[10]于 新, 杜银飞.考虑集料吸水率的水泥稳定碎石最大干密度及最佳含水量理论计算方法[J]. 公路交通科技, 2012, 29(3): 17-21.

[11]JTG E40-2007, 公路土工试验规程[S].

[12]JTG E51-2009, 公路工程无机结合料稳定材料试验规程[S].

[13]吴群英, 林 亮. 应用数理统计[M]. 天津: 天津大学出版社, 2004.

[14]张民选, 罗贤兵. 数值分析[M]. 南京: 南京大学出版社, 2013.

[15]孙麟杰, 蔺宏伟. 数据插值中的参数化新方法[C]// 中国工业与应用数学学会几何设计与计算专业委员会.第六届全国几何设计与计算学术会议论文集. 2013:154-156.

[16]彭永凯. Excel中用Newton迭代法求解土的最优含水率和最大干密度的方法[J]. 铁路计算机应用, 2014, (6): 67-68.

[17]王绍全, 高 斯, 何钰龙, 等. 基于微观分析的石灰改良粉质粘土击实特性[J]. 中外公路, 2015, (6): 246-248.

[18]边加敏. 石灰改良土灰剂量“衰减”影响因素研究[J]. 地下空间与工程学报, 2016, 12(1): 262-267.

[19]刘运兰. 路基回填土压实度影响因素试验研究[J]. 施工技术, 2015, (s1): 432-434.

[20]轩向阳, 陈海洋, 沈 超, 等. 强夯法和冲击碾压法在地基处理中的试验性研究[J]. 工程勘察, 2016, 44(1): 17-21.

Solution and Application of Compaction Characteristic Based on Different Data Processing Methods

ZHAOMin，LIGuang-guang，YINWen-jing

(School of Civil and Architecture Engineering，Xi’an Technological University， Xi’an 710032， China)

This paper combined with the practice of geotechnical testing regulations, based on a Jiangsu highway expansion project of subgrade soil random sampling test data, it compared and analyzed the two kinds of solving methods of compaction, and used the quadratic fitting curves method to solve compaction index of mixture with different lime content, preparation and compaction methods. Results show that: it’s suggested to use the three point two interpolation method or the two curve fitting method to solve the best compaction index of subgrade soil indicators. In order to ensure the reasonable compaction effect and avoid the maximum dry density being false partial large or the compaction degree being false partial small, the n-power of curve fitting should not be too high; When the lime content increased from 0 to 8%, the optimal water content was decreased in a trend of quadratic curve,the maximum dry density was increased in a trend of cubic curves; compared to the undisturbed soil, the maximum dry density of compacted soil is relatively larger, while the optimum moisture content is smaller; compared with light hammer, the maximum dry density of heavy compaction is much larger, while the optimum moisture content is much smaller.

compaction curve; fitting; maximum dry density; data interpolation; optimum moisture content

2016-03-31

2016-05-20

赵 敏(1970-)，女，陕西杨凌人，教授，硕士，研究方向为岩土工程、隧道与城市地下工程、岩土工程测试理论与技术(Email: zhaominxait@163.com)

U416

A

2095-0985(2016)06-0022-04