改进GM(1,1)模型在建筑沉降变形观测中的应用

2017-01-06李朝奎廖孟光

测绘通报 2016年12期

关键词：灰色背景建模

卜璞，李朝奎，廖孟光

(1. 湖南科技大学地理空间信息技术国家地方联合工程实验室，湖南湘潭 411201； 2. 湖南科技大学地理空间信息湖南省工程实验室，湖南湘潭 411201)

改进GM(1,1)模型在建筑沉降变形观测中的应用

卜璞1，2，李朝奎1，2，廖孟光1，2

(1. 湖南科技大学地理空间信息技术国家地方联合工程实验室，湖南湘潭 411201； 2. 湖南科技大学地理空间信息湖南省工程实验室，湖南湘潭 411201)

灰色预测模型GM(1,1)的建模思想是：原始序列(非负序列)经过一次累加生成后，形成一个单调递增数列，新序列中各数据点的连线可以用指数函数y=aebx进行拟合。根据这个指数函数可以推导出下一个累加值的预测值(即第一个预测期)，最后通过累减生成将累加序列预测值还原为原始序列预测值。本文通过对原始序列进行指数—幂函数变换，增加了原始序列的光滑度；并在灰参数求取过程中对原始序列赋以权重，利用迭代计算的方法推导出了模型精确背景值；最后通过使预测序列残差平方和最小的方法计算出最优初始条件，进而提出了一个改进后的GM(1，1)模型。利用改进后GM(1,1)模型对某大厦沉降监测数据进行模拟与分析，并对改进前后的模型进行对比与分析，结果表明，改进后模型的各项精度因子相比于传统模型均有所提高，且时间序列越往后的预测值，精度越高。

变形监测；灰色系统理论；预测模型；灰色改进模型

近年来我国经济腾飞，高大建筑物如雨后春笋般不断增加。为了保证建筑物可以正常使用及其安全性，对其建设及使用、维护过程进行系统的监测是十分必要的。20世纪80年代初，我国著名学者邓聚龙教授提出了灰色系统理论[1]。灰色系统理论的研究对象是灰色系统中分析、建模、预测、决策和控制的理论问题，经过多年的发展，这一理论已应用到社会科学与自然科学的众多领域中。

对灰色系统理论进行各种优化，建立新的算法模型解决问题有许多途径。邵红梅等通过研究初值选取对预测精度的影响构建了初值修正模型，文中虽然讨论了几种优化模型，但均基于初始值的选取，而没有考虑其他参数对模型精度的影响，优化效果提高不明显[2-3]。徐宁等根据背景值构造应满足无偏性和最小性的要求，针对满足指数增长规律的原始序列提出了新的模型算法[4]。蒋诗泉等利用函数逼近思想结合复化梯形公式提出了新的模型[5]。这两种方法均基于对背景值进行合理选择，但没有考虑到初始值的优化方案，如果初值选取不当会影响优化效果。

本文结合初值选取和背景值构造思想，通过对模型的初始条件增加附加因子、对背景值最小误差进行优化，建立综合模型，以提高GM(1,1)模型的预测精度。

一、传统GM(1,1)模型在建模过程中存在的问题

1. 传统模型中原始序列光滑度的问题

定理：一阶累加生成序列x(1)满足指数函数规律Aeak+B的充要条件是原始序列x(0)服从指数函数Mea(k-1)，x(0)(1)可以例外。

这个定理表明，在建立GM(1,1)模型时，就已经默认一阶累加序列服从指数分布规律，也即假设了原始序列服从指数分布规律[6]。

2. 传统模型中背景值有偏的问题

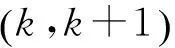
(1)

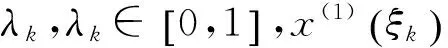
(2)

综上所述，灰色模型微分方程的离散形式可以表示为

(3)

式(3)变形后得到

(4)

根据微分方程的特解

(5)

可以解得λk的表达式为

(6)

可以看出，λk是与发展系数a有关的常数。

并且有

3. 传统模型中初始值选取的问题

传统GM(1,1)模型最终的响应函数为

(7)

二、改进后GM(1,1)模型的建模过程

根据前文中提到的传统灰色建模方法中出现的问题，结合笔者的研究，提出一种改进后的灰色预测模型的建模方法。

1. 数据转换

之前已经证明，只有当原始序列中的数据服从指数函数分布规律时，累加生成才能达到弱化随机性、强化规律性的目的，但在实际的变形监测数据中，数据点往往是离散分布，因此必须对原始序列进行转换之后再进行建模。比较常见的变换方法有加权变换、指数变换、对数变换、t次方根变换、对数—幂函数变换、动态摆动指数变换、黄金分割变换等[7]。

(1) 定义

本文选择对数—幂函数变换作为建模前数据变换的方法。

(2) 定理

(8)

上述定理表明，经过对数—幂函数变换的序列的光滑度要高于原始序列的光滑度。

2. 求取最优背景值

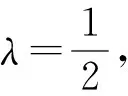
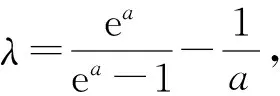
(9)

式中

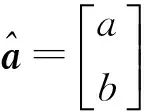
(10)

利用新算出的发展系数a可以继续计算背景值系数λ，如此循环计算，直到λ收敛至要求的精度为止。

3. 求取最优初始条件

对于模型最优初值条件的选取，采用徐涛[9]推导的过程，改进模型的时间相应函数设为

(11)

令

(12)

则时间相应函数可写为

(13)

用S来表示预测模型的残差平方和

(14)

解上述方程可得

(15)

4. 建立最终模型

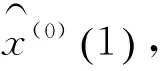
(16)

最后，根据灰色预测模型精度判定的原理，计算出模型的精度判定因子C、P，计算结束。

三、应用实例

某大厦项目是2004年7月在香港经贸洽谈会上签订的昆明市重点开发项目之一，总建筑面积71 886 m2，地上9层，地下2层。该建筑物总高度为50.3 m，地下室埋置深度为11.9 m。根据现场情况确认某大厦与周边5栋主要建筑邻接。大厦基坑距周围5栋主要建筑物距离偏小(10 m以内)，都处于影响范围内，而基坑开挖深度又较大(12 m)。因此，大厦的施工势必对其周边造成较大影响，必须对某大厦周边主要建筑物及地表的沉降变形进行严格监控，确保大厦周边建筑物及地表各类管线的稳定和安全。

该沉降观测从2005年3月开始，到2006年4月结束，历时一年多，累积沉降观测数据32期。鉴于与预测时间越近的数据对研究未来趋势的影响越大，并且灰色模型为少数据建模，选用某一观测点2005年7月8日—2006年4月22日的17期数据为数据背景，对灰色改进模型进行研究。

本文分别用传统灰色模型与改进后灰色模型对沉降数据进行模拟，两种模型得到的模拟结果与精度见表1。原始序列与模拟序列比较如图1所示。

对于一般精度要求的工程,绝对沉降的观测中误差可按低、中、高压缩性地基土的类别,分别选±0.5、±1.0、±2.5 mm。根据该大厦沉降观测实际情况,取绝对沉降观测中误差为±1.0 mm,容许误差为±2.0 mm。从表1及图1中可以看出，原始GM(1,1)模型与改进后GM(1,1)模型的模拟精度都可达到要求，改进后模型的各项精度指标明显高于传统模型，模拟值的残差随时间推移不断减小，说明模型的精度在逐渐提高。

四、结论

本文对传统GM(1，1)模型的建模机理进行了分析，通过对原始序列进行指数—幂函数变换，增加了原始序列的光滑度，使累加序列更加服从指数分布规律；从分析背景值有偏的原因入手，在灰参数求取过程中对原始序列赋以权重，利用迭代计算的方法推导出模型精确背景值；通过使预测序列残差平方和最小的方法，根据最小二乘原理，计算出最优初始条件，进而提出了一个改进后的GM(1，1)模型。利用新旧模型对同一组数据的模拟结果进行对比分析，结果表明改进模型在精度上有明显提高。这对于完善和拓展GM(1，1)模型具有积极的意义。

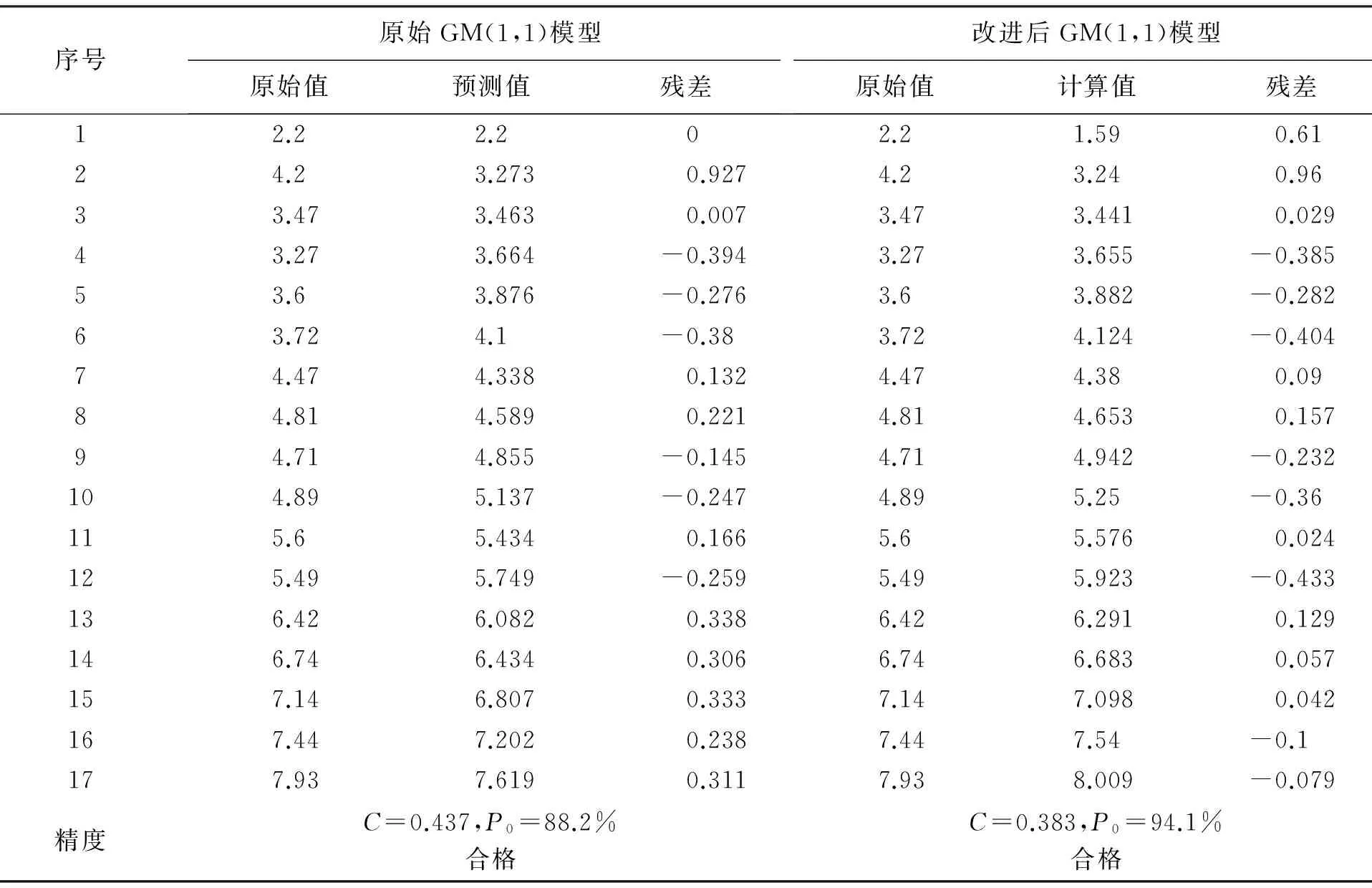
表1 原始GM(1,1)模型与改进后GM(1,1)模型模拟效果对比 mm

图1 原始序列与模拟序列比较

[1] 邓聚龙.灰色系统理论教程[M].武汉:华中科技大学出版社,1990.

[2] 邵红梅,杨建华,兰月新.基于初值修正的组合GM(1,1)模型及其应用[J].统计与决策,2015,422(2):89-90.

[3] WANG Y H,DANG Y G,LI Y Q,et al.An Approach to Increase Predication Precision of GM(1,1) Model Based on Optimization and the Initial Condition[J]. Expert Systems with Applications, 2010, 37(2): 5640-5644.

[4] 徐宁,党耀国,丁松.基于误差最小化的GM(1,1)模型背景值优化方法[J].控制与决策,2015,30(2):283-288.

[5] 蒋诗泉,刘思峰,周兴才.基于复化梯形公式的 GM(1,1)模型背景值的优化[J].控制与决策, 2014, 29(12): 2221-2225.

[6] 刘思峰,邓聚龙.GM(1,1)模型的适用范围[J].系统工程理论与实践，2000,11(5):121-124.

[7] 何君,杨国东.灰色预测理论在建筑物沉降中的应用研究[J].测绘通报，2013(3):63-64.

[8] 穆勇.灰色预测模型的精确解法[J].济南大学学报(自然科学版)，2003, 17(1):62-64.

[9] 徐涛,冷淑霞.灰色系统模型初始条件改进及应用[J].山东工程学院学报，1999,13(1):15-19.

The Application of the Improved Grey Prediction Model on Buildings Deformation Monitoring

BU Pu,LI Chaokui,LIAO Mengguang

2016-01-23

国家自然科学基金(41271390；41571374)；空间信息智能感知与服务深圳市重点实验室(深圳大学)开放基金

卜璞(1988—)，男，博士生，主要研究方向为测量数据处理与三维地理建模。E-mail：pup1988@126.com

卜璞，李朝奎，廖孟光.改进GM(1,1)模型在建筑沉降变形观测中的应用[J].测绘通报，2016(12)：60-63.