一种用于相机检校的黑白棋盘格角点提取算法

王海涛，洪 亮，谭成国

(1. 中国地质大学(武汉)国家地理信息系统工程技术研究中心，湖北 武汉 430074； 2. 湖北省基础地理信息中心(湖北省北斗卫星导航应用技术研究院)，湖北 武汉 430074； 3. 武大吉奥信息技术有限公司，湖北 武汉 430074)

一种用于相机检校的黑白棋盘格角点提取算法

王海涛1，2，洪 亮1，2，谭成国3

(1. 中国地质大学(武汉)国家地理信息系统工程技术研究中心，湖北 武汉 430074； 2. 湖北省基础地理信息中心(湖北省北斗卫星导航应用技术研究院)，湖北 武汉 430074； 3. 武大吉奥信息技术有限公司，湖北 武汉 430074)

黑白棋盘格作为一种人造平面控制条件，是一种重要的相机标定的参考条件。本文基于其角点的对称性、尺度不变性和领域特性，提出了一种有效的角点提取算法；同时针对格网边缘的特性，提出了双边缘的匹配算法，以提取高精度的角点；使用不同型号的相机、不同棋盘格制设备进行试验表明，本文提出的算法是一种具有很强鲁棒性的黑白棋盘格角点提取算法，可以高精度地定位角点。

黑白棋盘格；光束法平差；边缘匹配；直接线性变换；液晶显示器

将平面控制条件(平面格网板[1]、聚脂薄膜格网[2]、打印纸张格网[3]、LCD绘制圆[4]等)作为相机检校参考对象已被广泛应用，黑白棋盘格[5-8]更是被广泛使用。计算机视觉库OpenCV(open source computer vision library)[9]实现了黑白棋盘格角点的自动提取和文献[1](张正友，2000)标定的算法[1]，但其速度和提取效果有待改善，本文使用黑白棋盘格的自身特性提出一种可靠的高精度网格点提取算法。

棋盘格使用内角点(称为X角点)作为平面控制点，多采用Harris[7，10]、SUSAN[5，11]等算子提取，经处理后获得有效格网角点[12]。黑白棋盘格角点作为人造的特征，有其自身的特性，本文称为对称性和尺度不变特性[13]；另外提取的X角点与其邻域点有重要几何特性，本文称为邻域特性，利用该特性可对X角点进行错误检测。

采用光束法平差对相机检校，检校精度与X角点的提取精度相关。棋盘格网作为人造特征，格网黑白变换处形成阶跃边缘，边缘匹配可以高精定位边缘[17-18]，使用提取的边缘直线相交计算子X角点子像素坐标。本文将针对黑白棋盘格网进行详细分析，提出采用自适应边缘模板的边缘匹配方法，以提高X角点的定位精度。

一、黑白棋盘格网绘制及特点分析

黑白棋盘格(如图1—图2所示)使用两类角点(X角点)(图1、图2的点Ⅰ、Ⅱ)用于相机检校。

图1 绘制棋盘格

图2 投影后的棋盘格

1. X角点的相关性

截取图2中X角点的局部图并反向(见表1)。从表1可知，每类X角点原始局部影像与另一类点的反向图像相似。使用相关系数[19]可对X角点进行评估，同类X角点局部影像相关系数约等于1，不同类X角点局部影像相关系数约等于-1。

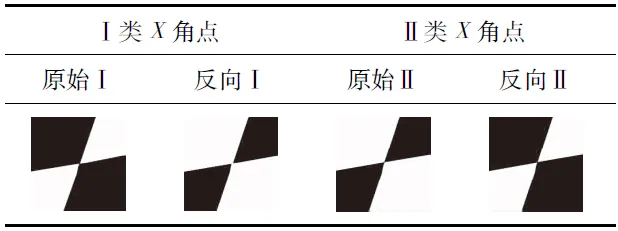
表1 X角点的局部图及反向图

2. X角点的对称特性

(1) 对称模式选择

改革开放至今，中国经济发展取得了较大成就，外向型经济发展的特征也愈加明显，特别是中国“入世”以后，中国对外贸易经济环境得到改善，凭借自身比较优势，对外贸易规模不断扩大，逐渐成为美国的第二大贸易伙伴。据中国海关总署公布2017年全年进出口统计数据显示，中国对美国贸易顺差2758亿美元，超过了2015年的2610亿美元的最高纪录，贸易顺差扩大13%，达到了中美贸易顺差的新高。中美货物贸易赤字不断扩大，美国部分经济学认为中美贸易发展导致美国制造业就业岗位缩减，并导致蓝领失业人口上升30%。 随着中国对美国贸易顺差，中美贸易摩擦持续升级，美国贸易保护主义抬头势头明显。

本文选择原点对称、X轴对称、Y轴对称、y=x轴对称、y=-x轴对称。图3为Ⅰ类X角点关于以上对称轴的示意图(Ⅱ类X角点同理)，点A对称点依次为B、C、D、E、F。

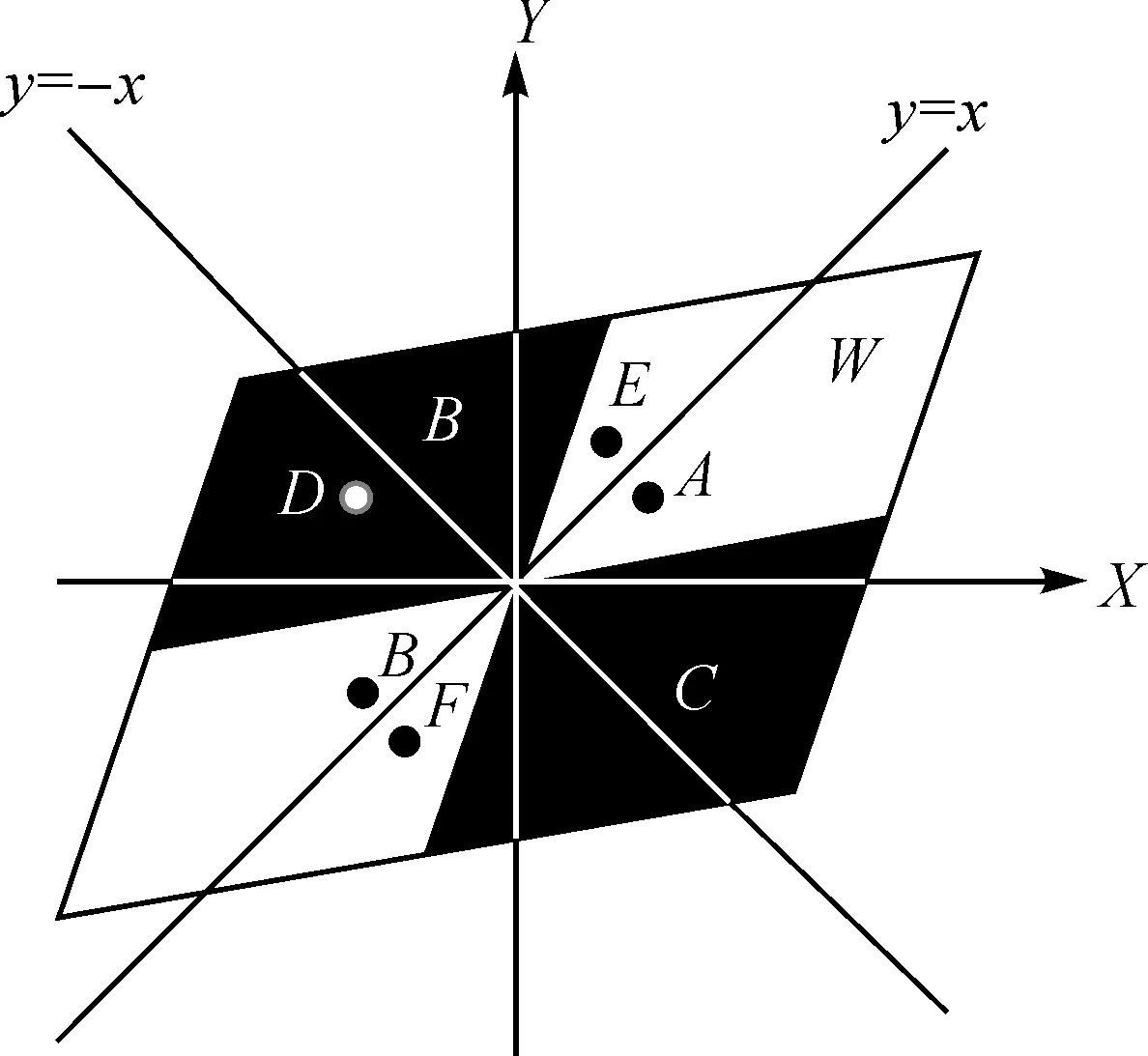
图3 X角点对称特性

(2) X角点对称特性及与像素值关系

表2 X角点对称特性像素值关系

(3) 图像对称变换及特性分析

使用图3的对称方式将X角点图像进行变换，变换后的图像表达式及特性见表3。图4(a)为黑白棋盘格网原始影像，图4(b)—(f)为表4变换方式表达的新影像。

图4 对称特性变换影像表达

(4) 对称特性影像变换及相似性

按照图3对称方式对X角点局部图像进行变换，以Ⅰ类X角点为例(Ⅱ类X角点同理)。为便于突出变换效果，给Ⅰ类X角点不同部分用字母A、B、C、D标识，变换后点结果见表4，可知原始影像关于原点对称，y=x轴与y=-x轴变换影像相似，x轴与y轴变换影像相似，对此相似性可用相关系数[19]进行评定。

3. X角点尺度特性

David Lowe在局部特征描述子提出尺度空间[13]的概念，本文使用影像金字塔的方式表达尺度。由表5可知，对于Ⅰ类X角点来说(Ⅱ类X角点同理)，在不同金字塔影像级别依然相似。不同尺度影像间的相关系数[19]应约等于1。

二、X角点子像素提取

1. 格网点边缘特征

将拍摄的黑白棋盘格影像灰度值作为高度值进行配色显示局部放大，效果如图5(a)所示。将图5(a)椭圆圈住部分显示剖面(如图5(b)所示)，图5(b)箭头标识部分对应图5(a)白色双线对应部分。另外，将图5(a)白色双线对应部分对应的边缘进行三维剖面显示，效果如图5(c)所示。

表3 影像变换及特性

表4 Ⅰ类X角点影像对称变换效果图

表5 X角点不同级别金字塔局部影像

图5 棋盘格剖面

分析图5可知，黑白棋盘格网黑白过渡地方的边缘为直线A和B的中间部分。下面分析X角点与格网边缘的关系，从图6可知，X角点的边缘需使用双线边缘表述。

图6 棋盘格双边缘

2. 边缘匹配

使用理论边缘模板进行边缘匹配[17，20]是一种有效点直线边缘定位方法。图7是文献[17—18]使用的一种边缘描述模板。

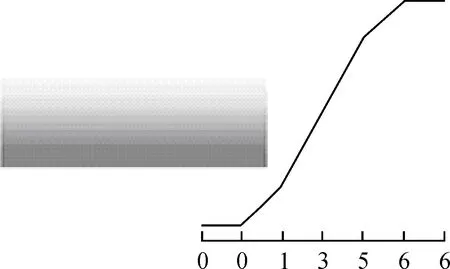
图7 边缘理论模板

从图5(b)剖面图可知，图7边缘理论模板不能充分表达棋盘格网影像黑白过渡区域边缘特征。图8是y=-tan-1x点曲线图，可以看出曲线与棋盘格网影像黑白过渡区域边缘特征相似。本文选择该函数描述棋盘格网影像黑白过渡区域边缘特征，则边缘灰度值与理论模板曲线的关系可表达为

(1)

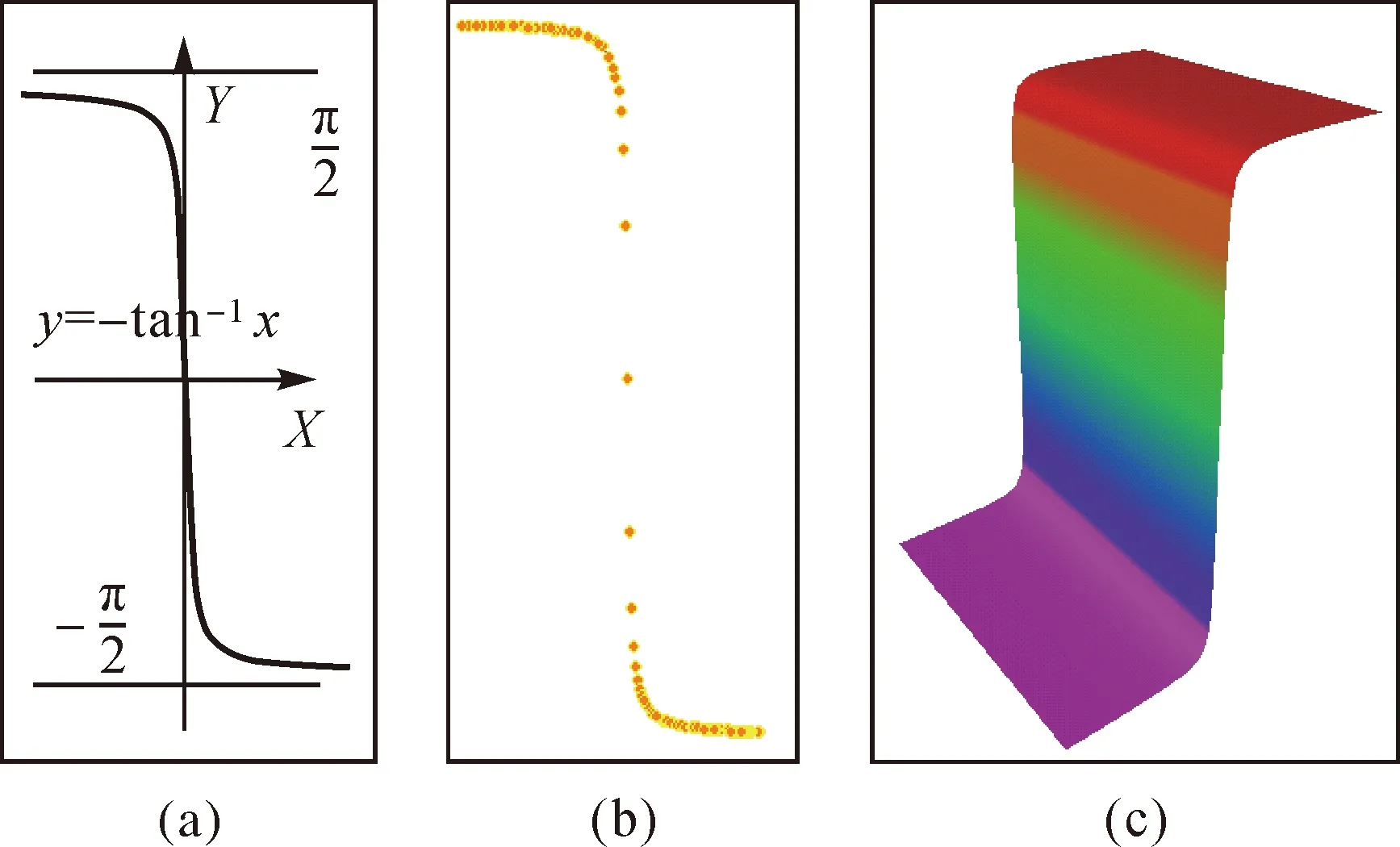
图8 函数曲线

图9 边缘匹配及提取角点(放大4倍)

三、试验分析

笔者采用摄影测量的自检校光束法进行平差[2，4]，相机的畸变模型采用文献[4]、文献[17]中的畸变模型参数。对未知数初值的解算有多种方法(如二维DLT、SVD分解等)，本文采用张永军[2]的二维DLT算法。对于LCD本身的误差[4]，采用附有限制条件的间接平差[4，20]模型进行平差计算。为克服自检校平差中的过度参数化[16]，采用小二乘平差的岭估计解法[21]。

本文使用不同型号的数码相机(见表8)、不同黑白棋盘格网的绘制设备(见表9)来验证算法。绘制黑白棋盘格X角点的数量为391个(23×17)。本文拍摄方式采用文献[4]的方法，拍摄效果如图10所示。

1. X角点提取试验

使用表8中型号的数码相机和表9中的绘制设备，拍摄12组影像，共1076张，验证X角点的提取算法。图11是一副拍摄影像的提取效果图，所有试验结果见表10。

表8 试验用数码相机

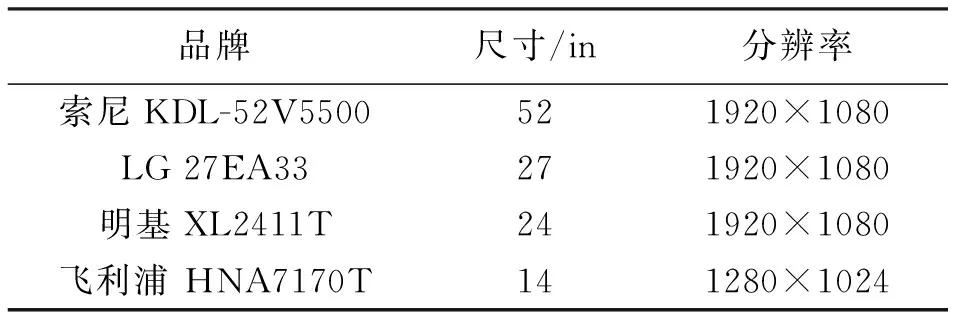
表9 格网绘制设备

图10 拍摄方式

图11 提取的X角点

2. 平差试验

对不同型号的相机、不同型号的黑白棋盘格网绘制设备开展平差试验。采用两种方式见表11—表15：①同一型号相机、不同型号黑白棋盘格网绘制设备；②同型号黑白棋盘格网不同型号相机、绘制设备。考虑到不同相机像元尺寸的不同，本文将精度统一到像素单位。

1) 同一型号相机，不同型号黑白棋盘格网绘制设备，见表11、表12。

表11 相机5D Mark Ⅲ(24 mm)

表12 相机ILCE-7R

2) 同型号黑白棋盘格网绘制设备，不同型号相机，见表13—表15。

表13 绘制设备KDL-52V5500

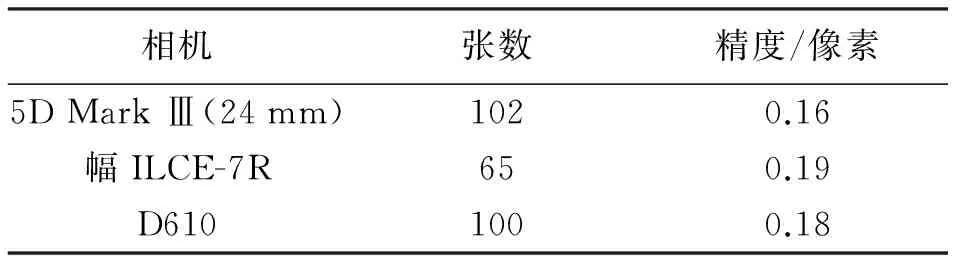
表14 绘制设备LG 27EA33

表15 绘制设备飞利浦 HNA7170T

四、结束语

通过不同型号数码相机、不同型号的绘制设备来绘制黑白棋盘格网的大量试验表明，基于X角点自身特性(对称性、尺度不变性、领域特性)的角点提取算法具有很强的鲁棒性，是一种有效的X角点提取算法。光束法平差验证表明，双边缘的边缘匹配算法可以提取高精度X角点，本文提出的边缘匹配算法是一种有效的边缘定位算法。

[1] ZHANG Z Y. A Flexible New Technique for Camera Calibration[J]. IEEE Trans. Pattern Analysis and Machine Intelligence, 2000,22(11): 1330-1334.

[2] 张永军. 利用二维DLT 及光束法平差进行数字摄像机标定[J]. 武汉大学学报(信息科学版),2002,27(6): 576-571.

[3] NOMA T, OTANI H, ITO T, et al. New System of Digital Camera Calibration,DC-1000[C]∥ISPRS Commission 5 Symposium. Corfu, Greece：[s.n.]，2002.

[4] 詹总谦.基于纯平液晶显示器的相机标定方法与应用研究[D]. 武汉：武汉大学,2006.

[5] 徐树奎,李国辉,张军,等. 基于多方向对称和匀质约束的SUSAN棋盘格角点检测算法[J].计算机科学,2011,38(9):248-253.

[6] 刘洋，王福利，常玉清,等. 黑白棋盘格角点检测算法[J].东北大学学报(自然科学版),2007,28(8):1090-1093.

[7] 王忠石，徐心和. 棋盘格模板图像角点的识别[C]∥2005年中国控制与决策学术年会(17CDC)论文集. 哈尔滨：[s.n.]，2005.

[8] 吴海滨,周英蔚,周雨润,等. 基于Hessian矩阵的黑白棋盘格角点检测[J]. 大气与环境光学学报, 2013, 8(5): 395-400.

[9] OpenCV. Intel OpenCV Computer Vision Library[EB/OL]. [2016-05-31]. http:∥www.intel.com/research/mrl/research/opencv.

[10] HARRIS C, STEPHENS M. A Combined Corner and Edge Detector[C]∥Proceedings Alvey Conference. Manchester, UK:[s.n.]，1988.

[11] SMITH S M,BRADY J M.SUSAN——A New Approach to Low Level Image Processing[J].International Journal of Computer Vision,1997,23(1): 45-78.

[12] 王忠石,徐心和. 棋盘格模板角点的自动定位[J]. 东北大学学报(自然科学版),2006,27(9):949-952.

[13] LOWE D G. Distinctive Image Features from Scale-Invariant Keypoints[J].International Journal of Computer Vision(S0920-5691),2004,60(2):91-110.

[14] TSAI. A Versatile Camera Calibration Technique for High Accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses[J]. IEEE J. Robotics and Automation,1987,3(4): 323-344.

[15] 冯文灏.近景摄影测量[M].武汉：武汉大学出版社,2002.

[16] 李德仁，袁修孝.误差处理与可靠性理论[M].武汉：武汉大学出版社，2002.

[17] HU X,ZHANG Z, ZHANG J. An Approach of Semiautomated Road Extraction from Aerial Image Based on Template Matching and Neural Network[J].International Archives of Photogrammetry and Remote Sensing, 2000, ⅩⅩⅩⅢ(B3/2): 994-999.

[18] 吴军.三维城市建模的建筑墙面纹理快速重建研究[D].武汉：武汉大学，2003.

[19] 张祖勋，张剑清. 数字摄影测量学[M].2版.武汉：武汉大学出版社，2012.

[20] 高士纯. 附有限制条件的间接分组平差模型与公式[J]. 武汉测绘科技大学学报,1996,21(1):36-40.

[21] 王乐洋，许才军，鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报(信息科学版)，2010, 35(11): 1346-1350.

[22] GRUEN A W. Adaptive Least Square Correlation: A Powerful Image Matching Technique[J]. South African Journal of Photogrammetry and Remote Sensing,1985, (14)3:175-187.

[23] 林宗坚,崔红霞,孙杰,等. 数码相机的畸变差检测研究[J]. 武汉大学学报(信息科学版),2005,30(2):122-125.

[24] 张祖勋.数字摄影测量与计算机视觉[J]. 武汉大学学报(信息科学版),2004,29(12):1035-1039.

An Effective Algorithm of the Black and White Checkerboard Corner Detection for the Camera Calibration

WANG Haitao，HONG Liang，TAN Chengguo

2016-06-21

国家863计划(2013AA122104)；测绘地理信息公益性行业科研专项(201512012)

王海涛(1976—)，男，博士生，高级工程师，研究方向为摄影测量与计算机视觉。E-mail：306550757@qq.com

王海涛，洪亮，谭成国.一种用于相机检校的黑白棋盘格角点提取算法[J].测绘通报，2016(12)：33-38.

10.13474/j.cnki.11-2246.2016.0396.

P237

B

0494-0911(2016)12-0033-06