GPS网平差的控制点有效性与选择研究
2017-01-06王秀萍蒋廷臣王继刚董春来李微晓
王秀萍,蒋廷臣,王继刚,董春来,李微晓
(1. 江苏省海洋资源开发研究院,江苏 连云港 222001; 2. 江苏海岸带环境研究所,江苏 连云港 222001; 3. 淮海工学院测绘与海洋信息学院,江苏 连云港 222005)
GPS网平差的控制点有效性与选择研究
王秀萍1,2,3,蒋廷臣1,2,3,王继刚1,2,3,董春来1,2,3,李微晓1,2,3
(1. 江苏省海洋资源开发研究院,江苏 连云港 222001; 2. 江苏海岸带环境研究所,江苏 连云港 222001; 3. 淮海工学院测绘与海洋信息学院,江苏 连云港 222005)
GPS网平差中起算控制点的质量与分布直接影响测量成果精度,解算未知控制点的坐标时,需要至少3个已知点,但并不是控制点越多越好。因此,合理地选择GPS网平差的控制点,对保证GPS控制网的精度起着至关重要的作用。本文结合工程案例,通过相似变换模型寻找质量最优的控制点,结合控制点数量与分布要求,选择出了该案例中最有效的控制点,可为其他类似工程提供参考。
GPS网平差;有效控制点;精度;相似变换
GPS测量成果在约束平差或联合平差前属于大地坐标系的WGS-84坐标系,然而我国建设工程测量多采用参心坐标系,故需将GPS点的地心坐标转换成参心坐标才能被使用[1-2]。一般采用的方法是利用已知控制点作为约束条件进行约束平差,把GPS网强制符合到控制点所在坐标系中[3]。由于这些已知控制点的坐标可能存在误差或粗差,如果不进行有效性检核控制处理,随意将这些控制点用作平差计算或坐标转换的约束条件,将得不到高精度的最终成果[4]。因此想获得高质量的定位成果,必须对已知控制点进行有效性挑选,剔除较大误差或粗差的控制点。有效性控制点指能用于网平差且其成果符合GPS规范要求的已知控制点。
解算未知控制点的坐标时,需要至少3个已知点,但并不是控制点越多越好。控制点的精度、个数及其分布对平差结果有一定的影响,控制点选择不当,将会引起GPS网的扭曲和变形,变形超过一定程度,就会明显降低GPS网的精度,是不能接受的。因此,合理地选择GPS网平差的控制点,对保证GPS控制网的精度起着至关重要的作用,也是GPS数据处理中解决的关键问题。本文以建立江苏连云港市灌南全县范围内的GPS控制网为例进行分析。
一、 GPS网平差的有效控制点选择原则
在GPS网布设中,已知控制点一般有若干个,为了得到高精度高质量的GPS网平差结果,必须选择出GPS网平差有效的起算控制点,其选择原则如下:
1) 精度:在进行GPS网数据处理后得到参心坐标或所需要的坐标时,将已知控制点坐标代入进行约束平差,从而得到最终的平差结果。由此可知,已知控制点的精度是外符合精度,决定了最终的成果质量。由于受到地面变形、人为因素的影响或建立这些控制点时的测量成果质量都会影响这些控制点的坐标,故需要在测量前对这些控制进行检核。
2) 控制点数量:根据公共控制点的选取与分布要求所建立的GPS网的成果与现有成果相似度最好时,则起算的公共控制点数量越多越好。反之,通常情况下一般选3~5个起算控制点为宜,用于实现基准的转换及必要的检核,这种处理方式既保证了新老坐标成果的一致性,也保持了原有GPS网的精度[5]。
3) 控制点分布:挑选有效控制点位置时,要纵观全局,切勿盲目选取。起算控制点不能位于网的一侧或某个角落,要平均分布于整个测区。两起算控制点间距离增大时,方位角较差和相对较差均减小,精度就会提高,当距离继续增大出现控制点各自分布在控制网边界时,会突然增大相对较差。选择位于网形的中央区域的起算公共控制点,而不能使它们分布在角落[4-6]。如果GPS网呈带状,则不应使起算控制点位于网的一端。
二、GPS网平差控制点有效性选择原理
1. 相似变换模型
相似变换模型(平面四参数模型)用于点在不同平面直角坐标系间的转换。设原坐标系下的平面直角坐标为(x1,y1),目标坐标系下的平面直角坐标为(x2,y2)。平面坐标转换涉及的4个参数分别为:2个平移参数,1个旋转参数 ,1个尺度参数[4]。其坐标转换模型如下
(1)
式中,x0、y0为平移参数,坐标单位均为m;α为旋转参数,单位为弧度;k为尺度参数。
将上式改写为
(2)
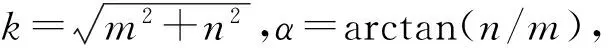
(3)
将式(3)写成矩阵形式为
L=BX
(4)

(5)
则误差方程为

(6)
若两坐标系中有n个控制点时,则可列出误差方程为
(7)
根据最小二乘原理,由观测方程列出误差方程进而组成法方程,根据法方程,得出计算四参数的公式为
(8)
式中,P为单位矩阵。求解转换参数,最后将转换参数回代入式(1)即可完成坐标转换[7]。
相似变换坐标转换方法是一种降维的坐标转换方法,即由三维空间的坐标转换转化为二维平面的坐标转换,避免了由于已知点高程系统不一致而引起的误差。在区域较小的情况下,应用二维四参数坐标转换将不同坐标系下的直角坐标进行转换[8]。
2. 最优控制点提取步骤
1) 将控制点坐标换算成高斯平面坐标或空间坐标。
2) 将全部控制点利用相似变换模型求取转换参数,再将求取的转换参数回代,求出全部控制点的转换坐标,进而计算各控制点的坐标残差。
3) 分析残差值较大(大于2倍残差中误差)的点的有效性,检查点位和成果是否正确,对残差较大特别是大于2倍残差中误差的点进行剔除后重新确定坐标转换控制点。
4) 重复上述步骤2)和3),回代残差到一定范围内和起算公共控制点在3~5个为止[3]。
另外,在上述步骤中,不要仅仅追求转换参数的回代精度,要同时兼顾网结构和图形强度。
3. 坐标转换精度估计
根据已知控制点和坐标转换模型计算出原坐标系到目标坐标系的转换参数,然后对坐标转换精度进行估计,精度评判如下:
1)V(残差)=转换坐标-已知坐标 。
2) 平面坐标x、y残差中误差,大地高H残差中误差(见表1)。坐标转换的精度通过求算转换参数的控制点的中误差体现。

表1 平面坐标x、y及大地高H残差中误差
三、案例分析
1. 测区概况和工作内容
(1) 测区概况
灌南县位于江苏省北部海滨城市连云港市的南翼,地处北纬33°59′—34°27′、东经119°07′—119°48′之间。东濒黄海,四市交界,西接宿迁的沭阳,南邻淮安的涟水,东与盐城的响水相连。县境最大直线距离东西长71 km,南北宽30 km。县域地势南高北低,西高东低,地面高程西南部达5.9 m,东部2.0 m,地面坡降1/18 000。东北东友引河一线高程仅1.6 m。由西南向东北逐渐倾斜,地形西宽东窄。
(2) 工作内容
在灌南县第二次土地调查期间布设的(基础控制测量网点D级GPS点25个)控制网基础上,引入三等以上水准点5个,建立覆盖全县范围内的E级GPS控制网,为全县下一步开展农村宅基地及集体土地建设用地使用权确权登记发证打下坚实的基础。
(3) 测区已有资料及利用
采用委托方提供的全县D级GPS控制点成果表,该套控制点属于1980西安坐标系,中央子午线为120°,1985国家高程基准。经实地调查、踏勘后,有25个控制点符合要求,分布如图1所示。这25个点现场保存完好、交通便利、视野开阔,周围没有大型障碍物和信号干扰设备,符合GPS观测要求,可以作为E级平面控制测量起算依据。由于该测区海拔较低,属于软土地基,故易受到地面变形影响,为有效建立GPS控制网,需对这25个控制点进行分析与挑选。

图1 控制点点位分布
2. 数据处理分析

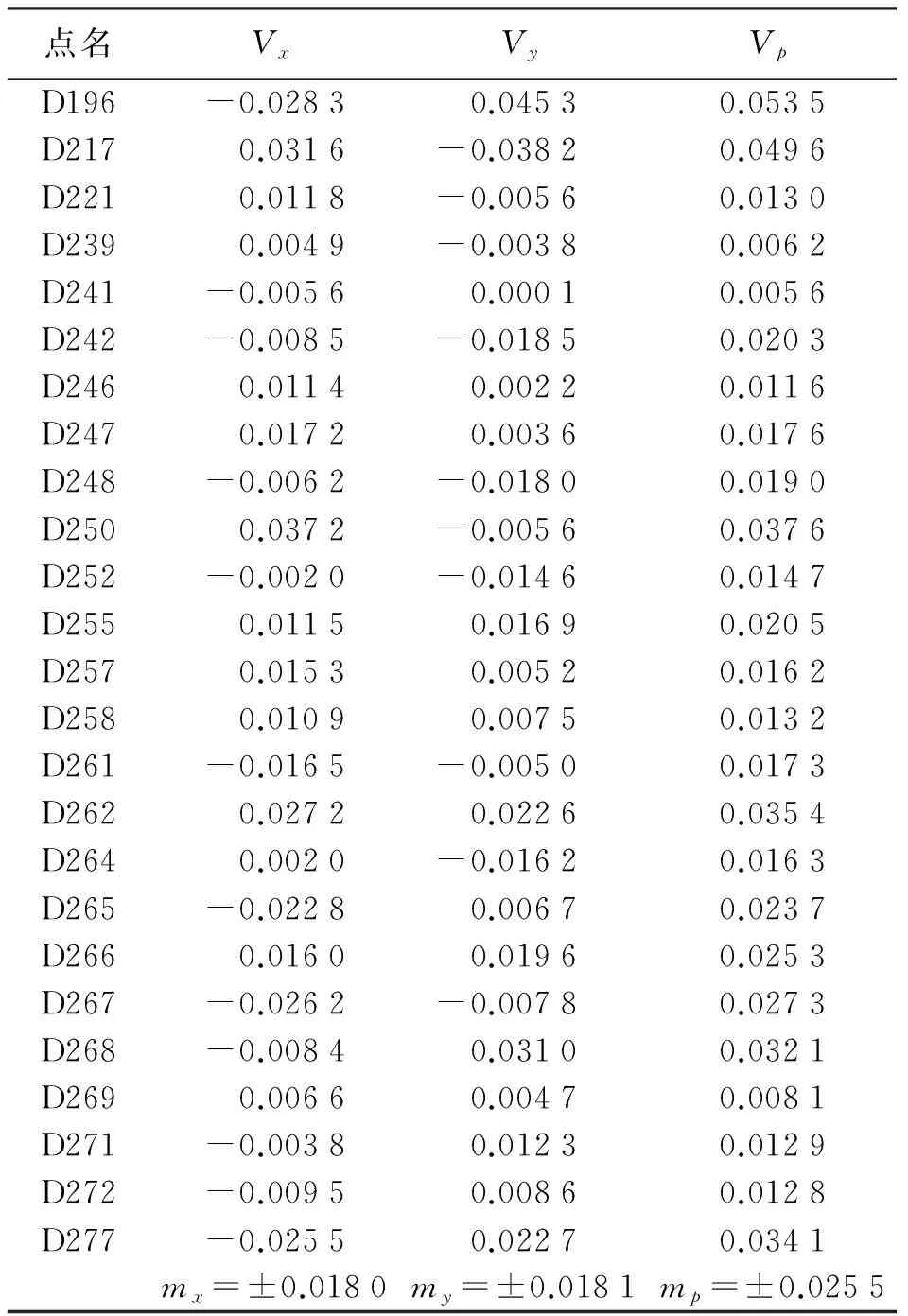
表2 25个公共点坐标转换残差结果 m

表3 5个控制点坐标转换残差结果 m
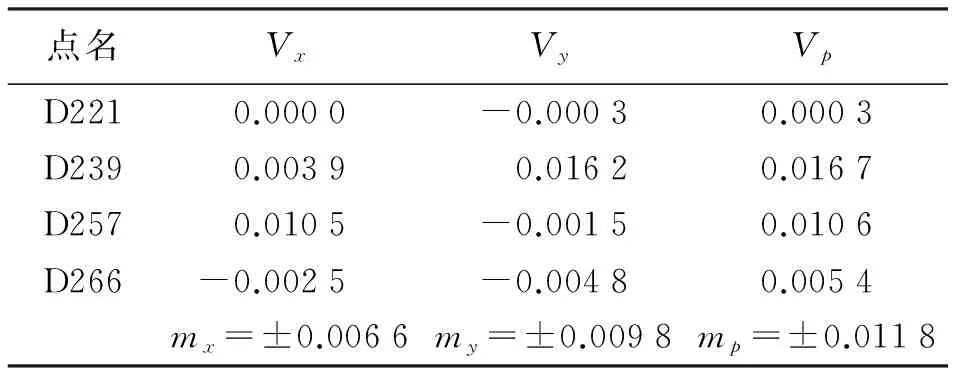
表4 4个控制点坐标转换残差结果 m
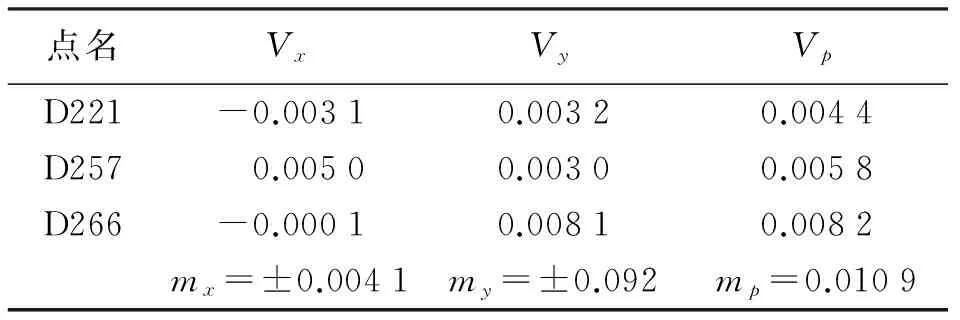
表5 3个控制点坐标转换误差结果 m
其中,表3是5个控制点坐标转换残差结果,其mx为5.6 mm,my为10 mm,mp为11.5 mm;表4是4个控制点坐标转换残差结果,其mx为6.6 mm,my为9.8 mm,mp为11.8 mm;表5是3个控制点坐标转换残差结果,其mx为4.1 mm,my为9.2 mm,mp为10.9 mm;根据表3—表5和控制点分布要求原则,在后续的约束平差中,如果选择5个控制点来进行计算,则5个控制点分别是:D221、D239、D257、D266和D269;如果选择4个控制点来进行计算,则4个控制点分别是:D221、D239、D257和D266;如果选择3个控制点来进行计算,则3个控制点分别是:D221、D257和D266。其相应的有效控制点分布如图2所示,这些有效控制点平均分布于整个测区,防止了误差的积累。

图2 最终选定的3~5个有效控制点分布图
四、结束语
本文以连云港市灌南县第二次土地调查GPS测量为例,结合GPS网平差控制点有效性选择原则,利用相似坐标变换模型,经过反复迭代,并根据控制点分布要求原则,在后续的约束平差中,如果选择5个控制点来进行计算,则5个控制点分别是D221、D239、D257、D266和D269;如果选择4个控制点来进行计算,则4个控制点分别是D221、D239、D257和D266;如果选择3个控制点来进行计算,则3个控制点分别是:D221、D257和D266。从结果证明,本文提出的方法对这样的工程案例是有效的,可以作为借鉴与参考。
[1] 刘学杰. 矿区GPS 网平差方案优化及精度分析[J].测绘通报,2016(6): 64-68.
[2] 党引群,王小瑞,黄功文,等. 起算点误差对GPS定位结果影响的分析[J]. 测绘标准化,2011,27(03):31-32.
[3] 焦立芬. 基于坐标转换重合点的分布、密度、精度与转换精度分析[J]. 测绘技术装备,2013,15(4):25-28.
[4] 陈舫益,熊登亮,邱云峰. GNSS控制网起算点的选择及分析[J]. 测绘与空间地理信息,2014,37(1): 200-202.
[5] 安卫,闫学静,王宝明,等. 一种平面四参数法坐标转换方法的实现[J]. 北京测绘,2012(5):53-55.
[6] 张恒璟,程鹏飞,孙小荣. 多项式拟合模型病态性问题的分析与应用研究[J]. 测绘通报,2012(7):35-38.
[7] 孙小荣,李明峰,刘支亮. 平面四参数坐标转换模型的改进与应用研究[J]. 大地测量与地球动力学,2015,35(1):132-135,144.
[8] 曹雪娟,阳凡林,张龙平,等. 不同区域范围的二维坐标系转换方法[J]. 工程勘察,2012(12):58-63.
[9] 吕红涛,左海玉,方广杰. 曲面拟合在GPS坐标转换中的应用[J]. 测绘与空间地理信息,2015,38(4):219-221.
[10] 辛明真,翟敏,褚恒滨. 基于整体最小二乘的平面坐标转换模型比较[J]. 工程勘察,2015(5):60-63,77.
Effectiveness and Selection of Control Point for GPS Network Adjustment
WANG Xiuping,JIANG Tingchen,WANG Jigang ,DONG Chunlai,LI Weixiao
2016-07-21
国家自然科学基金(41004003);江苏省自然科学基金(BE2016701); 连云港自然科学基金(SH1506);江苏省教改课题(JGZZ16_092);江苏省六大高峰人才项目(JNHB016);江苏省"333高层次人才"项目;连云港市"521高层次人才培养工程"项目;江苏省青蓝工程
王秀萍(1974—),女,硕士,实验师,主要从事GPS相关理论与方法研究。E-mail:wangxiuping502@sohu.com
P228.4
B
0494-0911(2016)12-0016-04
