寻求零件相似度的优化模型及梯度遗传算法

王 科

(成都工业学院 信息与计算科学系，成都 611730)

寻求零件相似度的优化模型及梯度遗传算法

王 科*

(成都工业学院 信息与计算科学系，成都 611730)

零件相似度的高效、精确的计算对于汽车的制造工艺有重要的实际意义。本文利用离散化的方法将零件相似性的问题转变为求相似度最大的非线性优化问题，然后通过构造拉格朗日函数将有约束优化转化为无约束优化问题，并结合梯度遗传算法对优化模型进行求解。最后，通过一些实例验证，说明该算法计算相对比较简单，收敛效果好。

零件相似度；优化模型；梯度遗传算法

由于当前国内汽车发展迅速，车型变化很快。在中国，一个主机厂至少每年要推出两款不同的车型，基本上才能赶上车市的变化节奏。而模具又是汽车开发周期的一个瓶颈，一个车型就冲压模具而言至少300多个冲压件，上千套模具，各个制件都有其成型特点。而对于一个车系来讲，虽然款式不同但其同类零件具有相似性，也有不同类别的车型在同类零件具有相似性。因此，对于模具供应商来讲，如果将其已经制作过的模具能够实现数字化库，而新接单的模具如果在这个库内能够查出相似的零件，那么这个制件所需模具的制作就可以借鉴库内的工艺方案。这样就节省了设计费用、缩短整个模具制造周期。因此对零件相似度的比对工艺的研究可以更好更快地查找到相似的零件，从而缩短设计周期。而且它还可以推广到其他相同或相似性产品的查找中，具有极强的推广意义。

零件相似度的比对本质上是三维形状相似的比较，也是当前搜索技术研究的热点。常用的三维相似算法有基于谱函数的相似算法[1]、基于概率统计的相似算法[2-3]以及基于目标识别的相似算法[3]、角点变换相似法[4]、递归分割生成有序满二叉树方法[5]等。基于谱函数的相似法通常使用傅里叶级数将离散的三维模型分解为前n阶项级数的近似和，虽然该方法具有很高的效率，但却不能分辨出相似的形状。基于概率统计的相似算法将采样点的数目和计算的花费进行了折中，采取减少采样点的数目来提高计算的效率，但计算精度也会随之降低。基于目标识别的相似算法只能测量有限的储存形态，并且要付出较高的储存和计算代价。角点变换通过角点匹配找到两张图相似的3个角点，由这3个角点为一个平面，在该平面下建立直接坐标系进行变换，这样就可以使得图形的形状与位置无关。而对于一个三维图形，要寻找角点，首先需要建立MLS平面，再通过角点匹配变换将两个不同坐标系下的图形变换到同一坐标下，然后通过梯度变换对图形进行细微调整，这样可以使减少图形的损失率，但角度变换的MLS平面和曲率的计算比较困难。递归分割生成有序满二叉树方法，即生成模型凸包围盒获取机械零件的初始位置并对其进行归一化变换，再生成自适应有界分割面对实体进行分割，检测分割过程中实体的几何和拓扑参数变化，递归建立有序满二叉树，结合工程特征构建特征矢量，比较特征矢量的相似性获得非根结点实体的相似度，从而获得各机械零件三维形状结构的相似度。但该方法分解起来比较困难，而且容易陷入局部最优解。

本文利用离散化的方法将零件相似性的问题转变为求相似度最大的非线性优化模型，然后通过构造拉格朗日函数将约束优化转化为无约束优化和梯度遗传算法相结合对优化模型进行求解，相对图形比较方法，该方法更高效，精度更高。

1 问题提出

在工程软件获取已有模具扫描图的数据的基础上，比较模具的相似度即对于任意的两件产品，当产品1与产品2放在同一朝向、同一平面上时，其高度差在2 cm内的区域面积。由于扫描过程中，产品摆放的位置不同、方向不同(见图1)。因此，根据工程需要，在定义的相似度原则下，将通过图形的旋转、平移来进行搜索查找。然而对于三维数据，数据量较多，如果采用穷举的方法在坐标系下直接进行旋转、平移是无法实现的。需要快速而准确的找到一个冲压模恰当的方向和坐标来与其他模具进行比较是解决该问题的关键。

图1 任意2件产品的摆放方式

2 模型分析与建立

对于任意的两件产品，设产品1为将要设计的零件，产品2为比对的零件。要判断产品2是否可用来设计产品1，问题转化为计算这两件产品的相似程度。由于产品大小不一，使得相似度的比较没有统一的标准。

2.1 目标函数的确定

设Sr表示绝对相似的面积，S1表示参照零件的总面积，以绝对相似面积与总面积之比定义为2个零件的相似度，则产品的相似度W可表示为

W=Sr/S1。

为了便于计算，将2件产品按照一定的距离进行离散化处理，产品2相对于产品1可用点的总数为绝对相似面积，产品1包含的点的总数为总面积。设产品1含有m个点，产品2含有n个点，则wij为m×n的0-1矩阵，显然m和n不宜取得过大。又由于相似的要求是高度差在2cm内的区域的面积，则L可适当取大一点，这里不妨取L=2.1 cm。将产品1投影到一个平面上，若长宽分别为l1和l2，则所取点数m应小于l1·l2/4。从而，

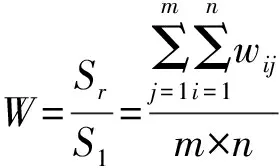
(1)

其中：1表示该点可用;0表示该点不可用。显然，相似度越大，则说明产品2的可用程度越高。则目标函数表示为：

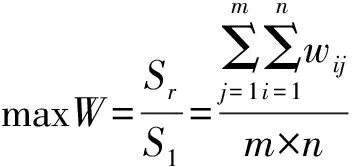
2.2 约束条件

对于相似度的比较，主要问题是零件摆放的位置和零件旋转的角度。以其中一个零件作为参考零件，另外一个零件作为候选零件，将候选零件进行旋转、平移，直到使得候选零件的相似度取得最大为止。所以，零件相似度的比较需要用到三维坐标的平移和旋转。

2.2.1 三维坐标的变换准备

1)三维坐标的平移变换

表示成矩阵的形式为：

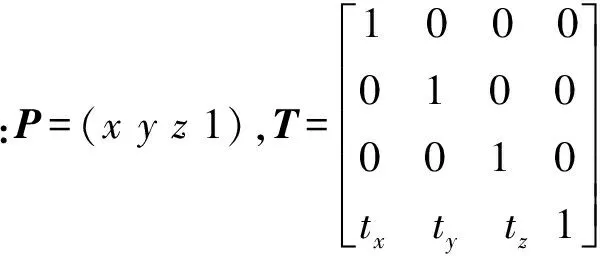
2)三维坐标的旋转变换：

①设绕x轴旋转α

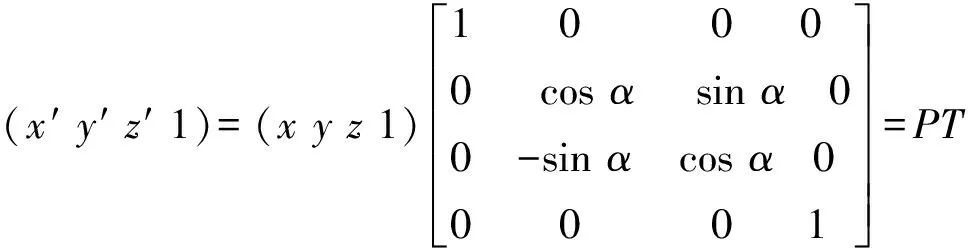
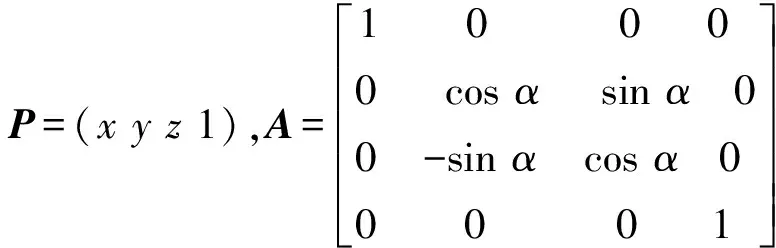
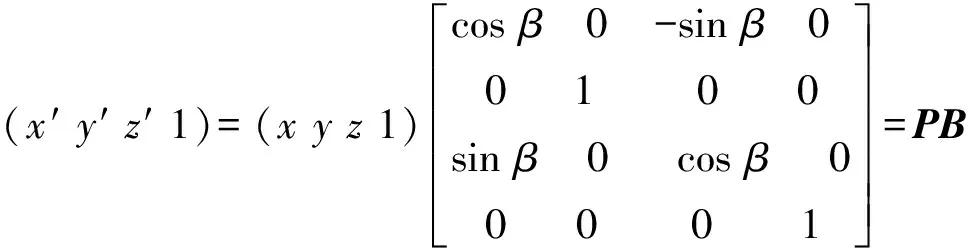
③设绕z轴旋转γ可表示为：

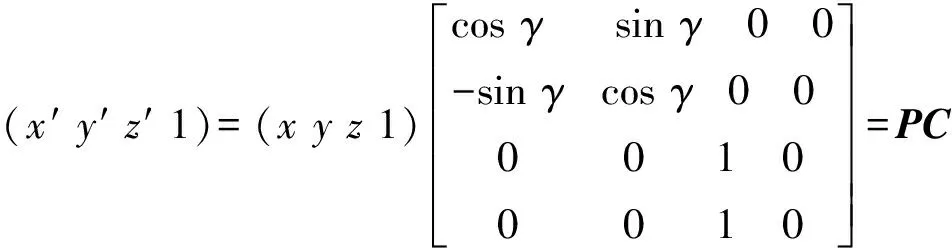
则三维坐标的变换公式为：(x′y′z′ 1)=PABCT

则

x′=tx-sinγ(ycosα-zsinα)+

cosγ(sinβ(zcosα+ysinα)+xcosβ)

y′=ty+sinγ(sinβ(zcosα+ysinα)+xcosβ)+

cosγ(ycosα-zsinα)

z′=tz-xsinβ+cosβ(zcosα+ysinα)

2.2.2 相同位置上的两点距离小于L为相似

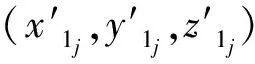
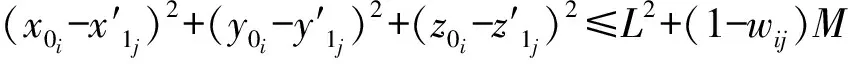
其中：M是一个非常大的数，即wij=1，该条件成立；wij=0时，该条件不成立。

2.2.3 优化模型的建立

综上所述，可建立优化模型为：

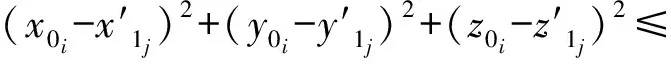
L2+(1-wij)M

x′=tx-sinγ(ycosα-zsinα)+

cosγ(sinβ(zcosα+ysinα)+xcosβ)

y′=ty+sinγ(sinβ(zcosα+ysinα)+xcosβ)+

cosγ(ycosα-zsinα)

z′=tz-xsinβ+cosβ(zcosα+ysinα)

其中：α,β,γ分别是绕x,y,z轴的旋转角。

3 算法分析

算法的关键是将不同三维图形通过平移、旋转变换，快速的转换到同一坐标下，以便进行比较。首先，将零件进行离散化处理，由于采集的图形点并不是规则的网格节点，本文采用反距离加权平均值法来生成均匀的网格节点。其次，对于非线性优化模型的求解，这里有旋转的三个方向的角度和平移的距离，考虑使用近似算法求解，但近似算法的收敛速度较慢，无法快速的得到最优解。于是，本文结合遗传算法的灵活性和梯度算法收敛速度快的优点，使用梯度遗传算法进行求解。

作拉格朗日辅助函数：

λ[(x′-x)2+(y′-y)2+(z′-z)2-L2-(1-wij)M]

(2)

3.1 反距离加权平均插值法

插值法是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况估算出函数在其他点处的近似值。常见的插值方法有拉格朗日(Lagrange)插值、分段线性插值、Hermite及三次样条插值、反距离加权平均插值法。

反距离加权平均插值法是一种局部插值法，其假设前提是未知值的点受较近观测点的影响比较远观测点的影响更大。由于水质的变化具有连续性特征，且越近的观测点其水质越接近，这里采用反距离加权平均插值法。

反距离加权插值指计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。当计算一个格网结点时，配给的权重是一个分数，所有权重的总和等于1.0。当一个观测点与一个格网结点重合时，该观测点被给予一个实际为1.0的权重，所有其它观测点被给予一个几乎为0.0的权重。换言之，该结点被赋给与观测点一致的值。其计算公式为：

(3)

其中：f(x,y)为坐标在点(x,y)插值后的值；fk为与点(x,y)间距为rk的观测点的值。

3.2 梯度遗传算法

1)生成初始种群α,β,γ,tx,ty,tz；

2)利用公式(2)计算各组值中对应的值；

3)以F值作为适应度函数，对α,β,γ,tx,ty,tz进行选择、交叉、变异；

5)使用梯度算法对以上结果进行优化；

6)重复步骤2—5有限次，则可求出该问题的近似最优解。

4 计算实例

本文数据来源于我校模具实验中心。以其中的10个零件为例，产品与产品经过旋转平移后的图形如图2—图10所示。

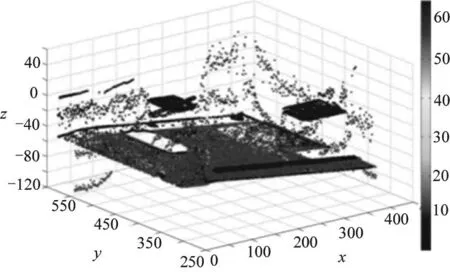
图2 旋转平移后产品2与产品1相似度为79.57%

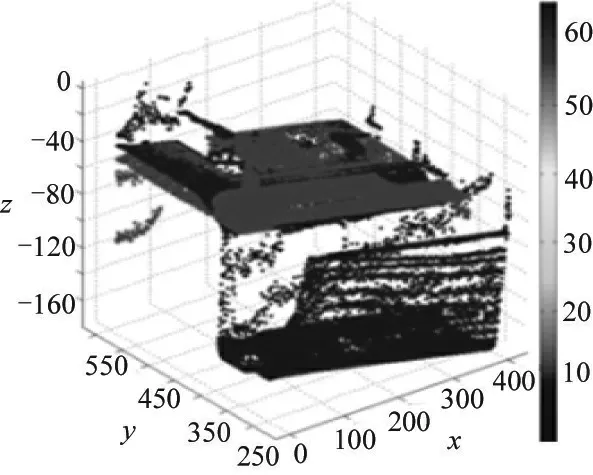
图3 旋转平移后产品3与产品1相似度为32.03%

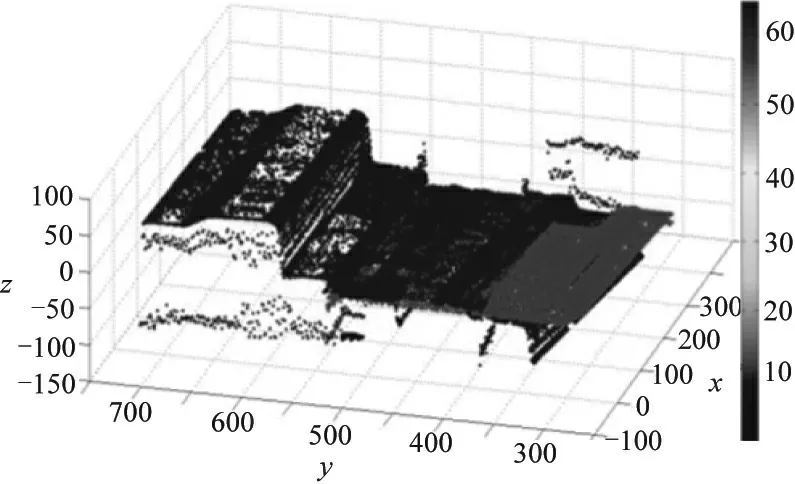
图4 旋转平移后产品4与产品1相似度为23.89%

图5 旋转平移后产品5与产品1相似度为21.47%

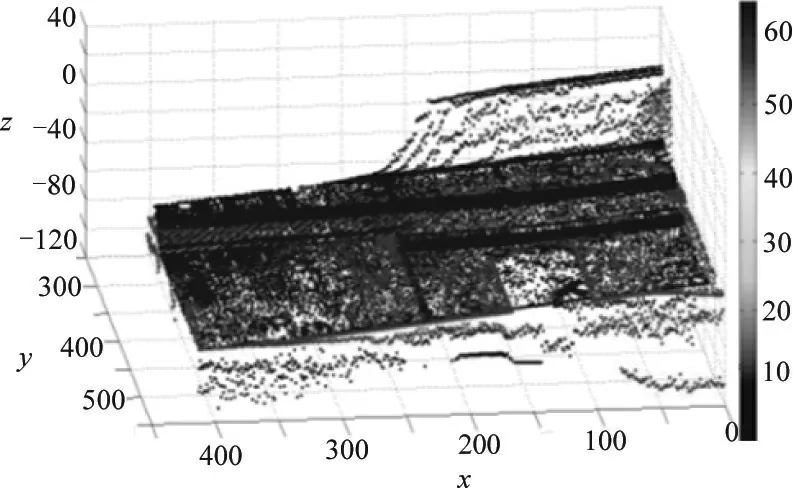
图6 旋转平移后产品6与产品1相似度为62.73%

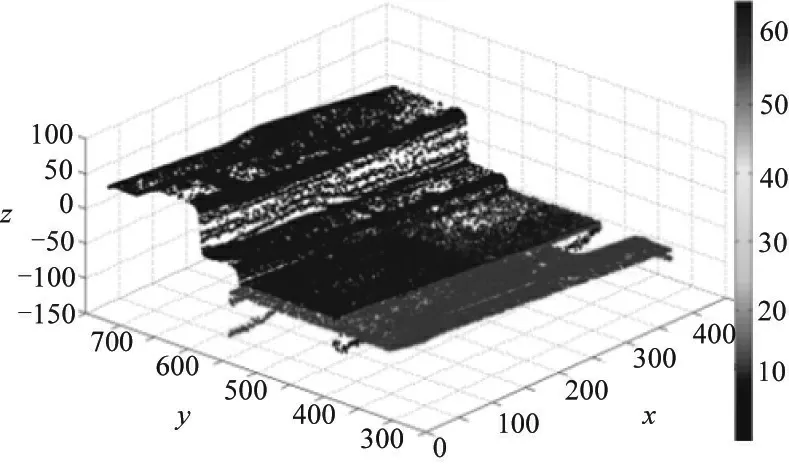
图7 旋转平移后产品7与产品1相似度为31.51%

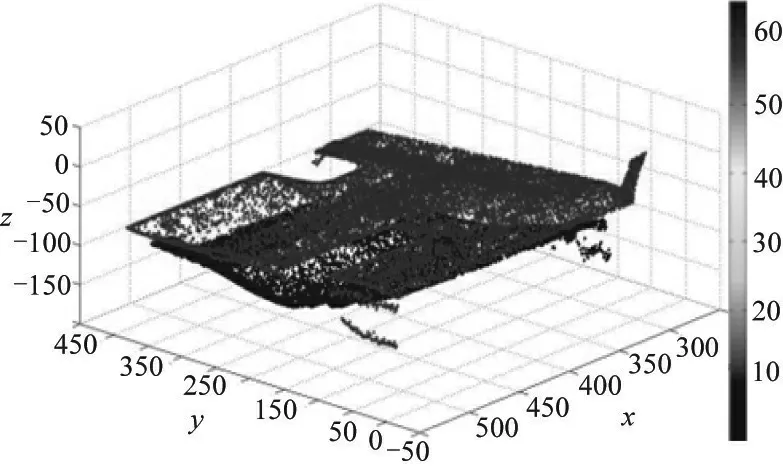
图8 旋转平移后产品8与产品1相似度为8.14%

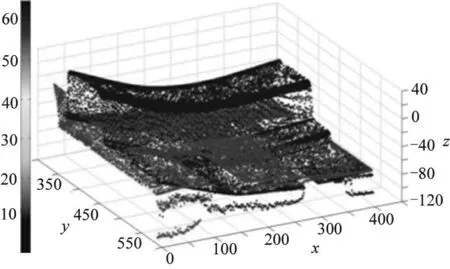
图9 旋转平移后产品9与产品1相似度为6.13%

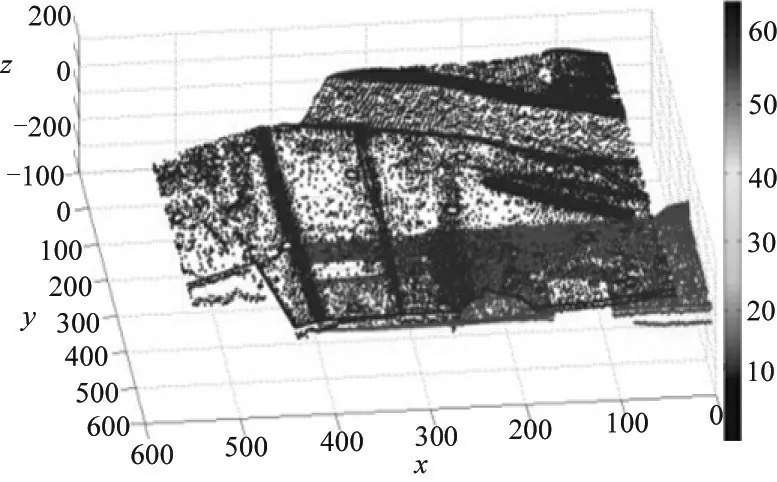
图10 旋转平移后产品10与产品1相似度为8.22%

从以上结果可以看出，通过旋转、平移的零件基本与比对的零件达到了使相似度达到最大的平面。

通过梯度遗传算法能够有效求解由零件相似度建立的优化模型，并且所涉及的理论和计算相对比较简单，收敛效果好。

[1] KAZHDAN M,FUNKHOUSER T,RUSINKIEWICZ S.Rotation invariant spherical harmonic representation of 3D shape descriptors[C]// Eurographics/acm SIGGRAPH Symposium on Geometry Processing.Eurographics Association,2003:156-164.

[2] OSADA R, FUNKHOUSER T, CHAZELLE B, et al.Shape distributions[J].ACM Transactions on Graphics, 2002,21(4):807-832.

[3] HONG T, LEE K, KIM S.Similarity comparison of mechanical parts to reuse existing designs[J].Computer-Aided Design,2006,38(9):973-984.

[4] CYR C M, KIMIA B B.3D object recognition using shape similiarity-based aspect graph[C]// Computer Vision, 2001. ICCV 2001. Proceedings. Eighth IEEE International Conference on.IEEE,2001:254.

[5] 陈德明,孙光民,许磊,等.基于角点检测的图像分割算法及在三维重建中的应用[J].计算机测量与控制,2009,17(1):173-176.

[6] 徐敬华,张树有.基于递归分割的机械零件三维形状结构检索方法[J].机械工程学报,2009,45(11):182-189.

[7] 李秀娟.求解多目标优化问题的随机梯度遗传算法[J].南京航空航天大学学报,2003,35(4):455-458.

Optimization Model and Gradient Genetic Algorithm for the Similarity of Parts

WANGKe*

(Department of Science and Information, Chengdu Technological University, Chengdu 611730, China)

Efficient and accurate calculation of parts similarity is of great practical significance to the automobile manufacturing process. In this paper, we used the method of discreting parts to translate similarity problem of nonlinear optimization model to its maximum similarity, then the constrained optimization into unconstrained optimization problem by constructing the Lagrange function. And it combined with the gradient genetic algorithm to solve the optimization model. Finally, it is proved that the algorithm is relatively simple and the convergence effect is good through some examples.

similarity of parts; optimization model; gradient genetic algorithm

10.13542/j.cnki.51-1747/tn.2016.04.020

2016-11-20

四川省教育厅项目“冲压模具产品寻求相似度模型及算法研究”(13ZB0044)

王科(1977— )，男(汉族)，四川金堂人，副教授，硕士，研究方向：模型与算法、数据分析、优化控制，通信作者邮箱：475169513@qq.com。

O242

A

2095-5383(2016)04-0078-05