基于DORIS数据的JASON-3卫星精密定轨

高园园，赵春梅，张小强

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266510；2.中国测绘科学研究院，北京 100830；3.中国航天科工信息技术研究院，北京 100070)



基于DORIS数据的JASON-3卫星精密定轨

高园园1，赵春梅2，张小强3

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266510；2.中国测绘科学研究院，北京 100830；3.中国航天科工信息技术研究院，北京 100070)

针对JASON-3卫星的精密定轨问题，采用了将DORIS RINEX格式的相位观测值转换为距离变化率的数据处理方法，基于统计定轨原理，精密确定了JASON-3卫星2016-03-01—2016-03-07和2016-03-06—2016-03-12两个7 d弧段的轨道。结果表明：通过重叠弧段检验，2弧段的定轨结果相差在7.5 cm左右，反映了定轨精度的可靠性。将2弧段的定轨结果与SSA轨道比较，轨道偏差在X、Y、Z方向上的标准差在3.12～4.71 cm范围内，其径向轨道偏差分别为1.55 cm、1.63 cm，满足海洋测高卫星定轨任务的需求。

JASON-3卫星；DORIS；DORIS 相位数；精密定轨；精度评估

0 引言

JASON-3卫星是由美国宇航局(National Aeronautics and Space Administration，NASA)，法国空间研究中心(Centre National d′Etudes Spatiales，CNES)，美国海洋和大气局(National Oceanic and Atmospheric Administration，NOAA)等机构合作研制的又一颗海洋测高卫星，于2016-01-17发射成功。JASON-3卫星采用了与JASON-2卫星相同的轨道设计，其轨道高度为1 336 km，倾角为66°，轨道周期为10 d。Jason-3卫星主要用于全球气候监测、业务海洋学和季节预报工作，是海洋测高卫星星座的重要组成部分。JASON-3卫星上装载有星基多普勒轨道确定和无线电定位组合系统(doppler orbitography and radio-positionng integrated by satellite，DORIS)接收机、全球定位系统(global positioning system，GPS)接收机和卫星激光测距(satellite laser ranging，SLR)反射器，用以对卫星进行精密定轨。

DORIS系统是由法国空间研究中心、法国大地测量研究所和法国国家地理研究所共同经过近十年的努力研制成功的，可以提供全弧段高精度轨道产品，主要用于卫星精密定轨和地面精确定位[1-2]。JASON-3卫星上装载了新一代DGXX-S接收机，考虑了JASON-2卫星的优势和不足。新一代接收机可以进行实时定位和精密卫星定轨，相比之前的DORIS接收机主要有以下优点：新一代DGXX-S接收机吸取了JASON-2卫星得到的经验与教训；DORIS的天线定位作了调整以联合多个潜在的发射通道作业；优化了太阳能电池的位置模型；远距离测距技术使得观测数据可以生成地极产品。JASON-3卫星的DORIS数据格式为与GPS观测数据格式类似的RINEX DORIS 3.0格式。数据类型为码观测值和相位观测值，其中相位观测值的精度可以达到几毫米，可以用于精密定轨和定位。

DORIS观测具有周期短、全天候、数据多、信标站分布均匀等优点[3-4]。目前，国内外很多学者对DORIS系统及其精密定轨进行了许多成熟的研究[5-17]：文献[5]基于DORIS跟踪数据实现对JASON-1和JASON-2的径向定轨精度达到1 cm；文献[6]计算的三维位置精度分别达到了2.7 cm和2.9 cm；文献[7]基于HY-2A卫星的DORIS数据，实现了径向1.6 cm的平均定轨道精度；文献[8]研究了相位观测数据与传统的DORIS距离变化率数据的转换方法，并利用DORIS3.0格式的数据实现了JASON-2卫星的cm级定轨；文献[9]研究了DORIS系统RINEX观测值模型的建立并在此基础上进行了JASON-2卫星的定轨，径向精度达到1 cm量级.本文针对2016-01-17日发射的JASON-3卫星，利用其DORIS RINEX 3.0格式的数据进行了精密轨道确定，并对其定轨结果进行了比较和分析。

1 基本公式与数据处理

1.1 卫星运动方程

卫星在围绕地球的运动过程中会受到多种作用力的影响。总的来讲，这些作用力可以分为两大类：一类为保守力；另一类为发散力。保守力包括地球引力、日、月、行星对卫星的吸引力以及地球的潮汐现象导致的引力场的变化等。发散力包括大气阻力、地球红外辐射以及卫星姿态控制的动力等[10]。

卫星在地心天球参考坐标系中的运动方程[11]为

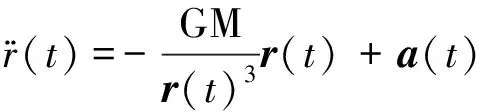
(1)

1.2 RINEX数据处理

早期的DORIS 2.2格式数据是经过初步定轨并计算误差改正项之后发布给用户的，获取定轨数据通常需要一定的时间延迟[12]。新的DORIS RINEX 3.0格式数据则主要包括不加任何误差修正的原始观测双频相位和伪距测量数据，其最大的优点就是可以很快获得，并且每天发布，直接用于定轨[13]。DORIS数据格式3.0与GPS数据的RINEX格式类似。RINEX数据文件提供双频伪距和相位观测值，第一频率标称值为2.036 25 GHz，第二频率标称值为400.125 MHz，第二频率数据主要用于双频电离层改正[9]。由于频率越高波长越短、测量精度越高，因而高精度轨道计算一般采用高频2 GHz相位数据。本文基于JASON-3卫星的RINEX格式的相位观测数据，利用文献[8]中提到的方法进行数据处理，基本过程为：

1)选取观测文件中10 s开始的观测序列，将相位观测值转换为距离变化率数据；

2)数据转换的过程中对数据进行预处理，剔除粗差较大的数据；

3)将各历元时刻的距离变化率数据进行DORIS接收机天线相位中心偏差修正。

在步骤3)中需要将星固系下的DORIS接收机与卫星质心间的偏差α转换到J2000惯性系中.涉及到的转换公式为：

α′=R(t)·α；

(2)

R(t)=[g1，g2，g3]T；

(3)

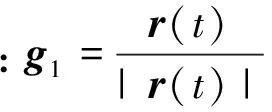
2 定轨数据及策略

2.1 定轨数据

定轨过程采用RINEX DORIS3.0格式数据，定轨弧长选为7 d，分别为01弧段：2016-03-01—2016-03-07；02弧段：2016-03-06—2016-03-12。弧段之间有两天重叠，具体如图1所示。

图1 观测数据及重叠轨道示意图

2.2 定轨策略

卫星精密定轨策略是卫星精密定轨中首要解决的问题[15]。本文关于JASON-3卫星的研究基于CASMORD软件平台。采用统计定轨原理和最小二乘批处理算法[15]。DORIS地面信标站坐标采用ITRF2008框架。

卫星定轨选取的力学模型及定轨策略如表1。

表1 力学模型及解算参数

3 定轨结果与精度分析

本文对统计定轨的精度评定的方法分为内符合精度检核和外符合精度检核两种方法。内符合精度采用检验观测资料的拟合程度和重叠弧段比较的方式。外符合精度通过与CNES计算的精密轨道(以下简称为SSA轨道)进行比较，对JASON-3卫星的DORIS定轨结果进行评估和分析。

3.1 观测资料的拟合程度

通过本文选取的定轨策略，分别对01、02弧段进行了精密轨道确定。各弧段的台站数、观测值的数目及观测值残差均方根误差的统计结果如表2所示。

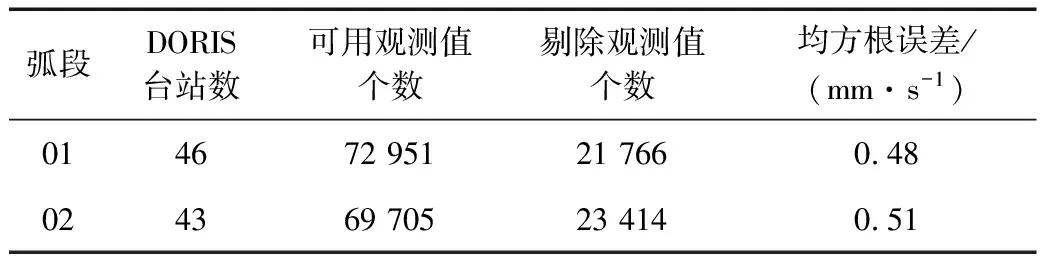
表2 01、02弧段观测残差统计

从表2中可以看出虽然2弧段的时间不同，因而观测量有差异，但是由于采用相同的定轨策略，2弧段的观测值残差均方根误差基本一致，也就表明定轨道精度相同。同时01弧段相比02弧段观测资料的拟合程度较好，亦即定轨内符合精度较好，约为0.48 mm/s。从2弧段参与运算的DORIS台站的数目和可用观测值的数量可知，01弧段观测资料的质量较好，在预处理和定轨软件计算中剔除的数据量较少，也是造成2弧段定轨内符合精度差异的原因之一。

3.2 重叠弧段的比较

对于01、02两个弧段采用相同的定轨道策略，分别进行独立轨道确定，弧段间有2 d的轨道重叠。重叠时段轨道偏差如图1所示，具体的统计结果见表3。

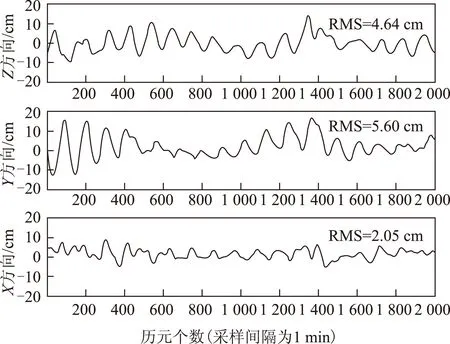
图2 01、02弧段重叠轨道检验

表3 重叠弧段轨道偏差统计 cm

从图2和表3可以看出，重叠弧段的定轨结果相差在7.5 cm左右。图2中均方根(root mean square，RMS)值为轨道对比得到的残差值。虽然2 d的重叠弧段的观测数据相同，但是这两段轨道是通过两次独立定轨过程得到的，即可以认定此两天的重叠轨道不相关，所以，重叠轨道的吻合程度可以反映轨道的定轨精度[16]。

3.3 定轨结果与SSA轨道比较

JASON-3的SSA轨道由DORIS国际服务组织(International Doris Service，IDS)的官方网站提供的，是法国CNES DORIS数据处理中心计算的事后精密轨道。01弧段的定轨结果与SSA轨道之间的差异如图3所示。图中，横坐标为历元个数，纵坐标为轨道差值(单位为cm)，不同颜色的曲线分别表示在X、Y和Z3个方向上的坐标差值。图3中RMS值为轨道对比得到的残差值。具体统计结果如图表4所示。

图3 01弧段定轨结果与SSA轨道的比较

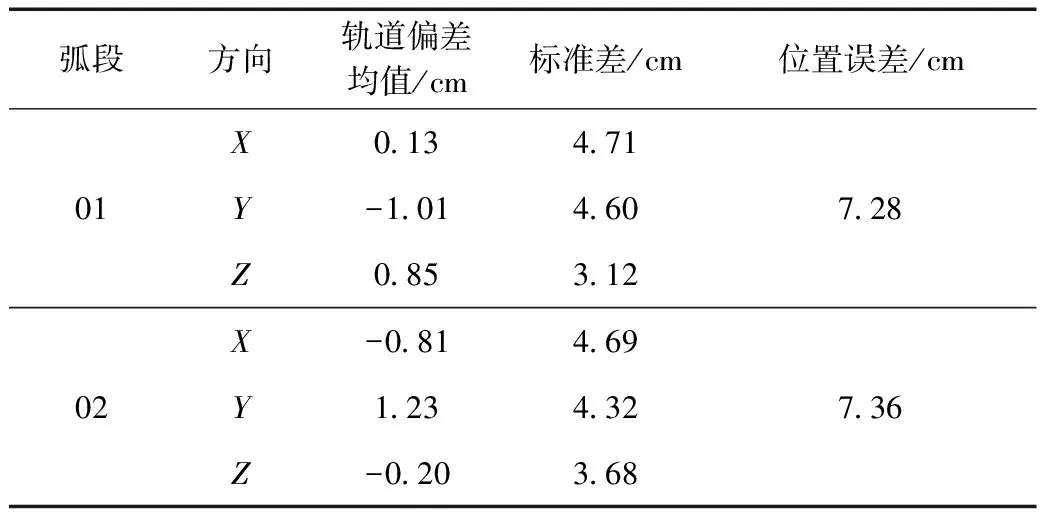
弧段方向轨道偏差均值/cm标准差/cm位置误差/cm01X013471Y-101460Z08531272802X-081469Y123432Z-020368736

从图3和表4中可以看出，通过与SSA轨道比较，对于01、02弧段的定轨结果，在X、Y、Z3个方向上标准差都在cm级，说明定轨精度达到厘米级别，符合精度要求。2弧段在Z方向上的定轨精度较好，在X、Y方向上的定轨精度相当。

由于JASON-3为海洋测高卫星，其径向(R方向)定轨精度是卫星任务中关注的首要问题。图4反映了01、02弧段的定轨结果与SSA轨道在R方向上的轨道差异变化，红色曲线和蓝色曲线分别为01、02弧段R方向的轨道偏差。2弧段的定轨结果与SSA轨道相比在R方向上的残差标准差分别为1.55 cm、1.63 cm，满足海洋测高卫星对径向定轨道结果的需求。

图4 01、02弧段定轨结果与SSA在径向上的差异

4 结束语

本文主要研究了基于DORIS系统的JASON-3卫星精密定轨问题，通过检验观测资料的拟和程度、重叠弧段比较和与精密轨道对比的方式验证了定轨的有效性。

采用相同的定轨策略，分别对01、02弧段进行精密轨道确定，2弧段的观测值残差均方根误差在0.40～0.55 cm范围内。其中01弧段的观测资料的数据剔除率较小，参与定轨的台站数目多，进而观测资料的拟合程度较好。通过重叠弧段检验，01、02弧段的定轨结果相差在7.5 cm左右，反映了定轨精度的可靠性。将2弧段的定轨结果与SSA轨道比较，轨道偏差在X、Y、Z方向上的标准差在3.12～4.71 cm范围内，其径向轨道偏差分别为1.55 cm、1.63 cm，对于最关心卫星径向定轨精度的海洋测高卫星来说，完全满足其定轨需求。

[1] 李培佳.利用DORIS测轨系统实现高精度定轨[J].飞行器测控学报，2010，29(3)：58-64.

[2] AURIOL A，TOURAIN C.DIRIS system：The new age [J].Advances in Space Research，2010，46(46)：1484-1496.

[3] 张强，廖新浩，黄瑸.两种观测技术综合精密定轨的探讨[J].天文学报，2000，41(4)：347-354.

[4] 王慧君.高精度DORIS定轨系统[J].光电系统，2010(3)：27-31.

[5] NIKITA P Z，FRANK G L，MAREK Z，et al.DORIS/SLR POD Modeling Improvements for Jason-1 and JASON-2[J].Advances in Space Research，2010，46(12)：1541-1558.

[6] CLAUDIA F，MICHIEL O，TIM S，et al.Generating precise and homogeneous orbits for Jason-1 and JASON-2[J].Advances in Space Research，2011，48(1)：152-172.

[7] 周旭华.HY2A卫星的GPS/DORIS/SLR数据精密定轨[J].武汉大学学报·信息科学版，2015，40(8)：1000-1011.

[8] 赵春梅.基于DORIS数据的JASON-2卫星精密定轨分析[J].地球物理学进展，2013，28(1)：49-57.

[9] 李文文.利用DORIS相位数据的JASON-2卫星精密定轨[J].武汉大学学报·信息科学版，2013，38(10)：1207-1211.

[10] 李济生.人造卫星精密轨道确定[M].北京：解放军出版社，1995：1.

[11] 孔巧丽.HY-2卫星星载DORIS和SLR的cm级综合精密定轨仿真研究.武汉大学学报·信息科学版，2013，38(6)：694-699.

[12] 朱俊.HY-2卫星DORIS厘米级精密定轨[J].宇航学报，2013，34(2)：163-169.

[13] MERCIER F，CERRI L，BERTHIAS J P.JASON-2 DORIS phase measurement processing[J].Advances in Space Research，2010，45(12)：1441-1451.

[14] 盛传贞.JASON-2卫星精密轨道确定：GPS，SLR和DORIS分析[J].中国科学，2013，43(2)：219-224.

[15] CHI-TAI H，CHUH-CHIH K，WANG C L，et al.Jason-1 precision orbit determination using GPS combined with SLR and DORIS tracking data[J].Rock and Soil Mechanics，2003，32(10)：2917-2916.

[16] 秦建.JASON-2卫星星载GPS数据cm级精密定轨[J].武汉大学学报·信息科学版，2014，39(2)：137-141.

[17] LUTHCK S B，ZELENSKY N P，ROWLANDS D D，et al.The 1-centimeter orbit：Jason-1 precision orbit determinationusing GPS，SLR，DORIS and altimeter data[J].Marine Geodesy，2003，26(3)：399-421.

JASON-3 orbit determination based on DORIS data

GAO Yuanyuan1，ZHAO Chunmei2，ZHANG Xiaoqiang3

(1.College of Geomatics，Shandong University of Science and Technology，Qingdao，Shandong 266510，China；2.Chinese Academy of Surveying and Mapping，Beijing 100830，China；3.China Aerospace Science and Information Technology institute，Beijing 100070，China)

In view of the precise orbit determination of JASON-3，based on statistical orbit determination theory，the data transformation method from phase observation data to traditional DORIS distance rate were used，and the orbit of JASON-3 were determined from 1 March to 12 March in 2016.The orbit is composed of two seven days arcs which overlap time of two days.The results indicated that by the overlapping arc inspection，the difference between the result of the orbit of the two arc is about 7.5 cm，which reflects the reliability of the orbit determination accuracy.when compared the result of the orbit determined in this paper with SSA precise trajectory file，the root-mean-square of the orbit deviation inX，Y，Zdirection is within the scope of 3.12 cm to 4.71 cm，and the values in radial direction are 1.55 cm，1.63 cm respectively，which meet the demand of the task of ocean altimetry satellite orbit determination.

JASON-3；DORIS；DORIS phase measurements；Precise Orbit Determination；accuracy evaluation

2016-00-00

国家自然科学基金项目(41274018)；科技部基础性工作专项(2015FY310200)。

高园园(1991-)，女，山东济宁人，硕士研究生，研究方向为卫星精密定位与定轨。

高园园，赵春梅，张小强.基于DORIS数据的JASON-3卫星精密定轨[J].导航定位学报，2016，4(4)：55-58,87.(GAO Yuanyuan，ZHAO Chunmei，ZHANG Xiaoqiang.JASON-3 orbit determination based on DORIS data[J].Journal of Navigation and Positioning，2016，4(4)：55-58,87.)

10.16547/j.cnki.10-1096.20160411.

P228

A

2095-4999(2016)04-0055-05