基于模糊理论的悬浮火箭控制器设计与仿真①

胡思翱，杨 军，潘 涛，陈华兵

(中国航天科技集团公司四院四十一所，西安 710025)

基于模糊理论的悬浮火箭控制器设计与仿真①

胡思翱，杨 军，潘 涛，陈华兵

(中国航天科技集团公司四院四十一所，西安 710025)

悬浮火箭采用推力矢量控制方式，箭体俯仰、偏航通道存在控制耦合作用，模型参数在飞行过程中存在时变性，传统的PID控制算法无法取得较好的控制效果。为此，以模糊理论为基础，分别设计了参数自整定PID控制器及模糊控制器。利用MATLAB构建悬浮火箭俯仰-偏航联合控制回路仿真系统，在俯仰、偏航通道之间存在20%控制耦合作用、加入随机干扰及模型参数时变的条件下对两种控制器的性能进行检验。由仿真结果可看出，参数自整定PID控制器具有较好的鲁棒性，能够抑制系统中存在的干扰作用，控制性能更优。利用Simulink搭建悬浮火箭的六自由度仿真模型，由仿真结果可看出，采用参数自整定PID控制器后，悬浮火箭能够快速抑制干扰并迅速响应俯仰角指令。

模糊控制器；参数自整定；PID控制器；悬浮火箭

0 引言

悬停式有源诱饵是一种通过模拟舰艇雷达信号，将反舰导弹诱骗至舰艇外安全区的反导防御武器[1]。主要由悬浮火箭及其搭载的电子干扰设备构成。由于悬浮火箭弹体无翼面，飞行速度低，气动力小，弹体严重静不稳定，常规的气动力控制方式已不适用。针对悬浮火箭这些特性采取的控制方式是通过推力矢量完成弹体俯仰和偏航方向姿态控制。在这种控制方式下，悬浮火箭的俯仰、偏航通道存在控制耦合作用，加之飞行过程中模型参数的时变性，传统的PID控制算法无法取得较好的控制效果。

模糊控制是以模糊集合论为理论基础，将工程技术人员的经验总结出的控制规则用计算机予以实现的一种自动控制方法。与传统控制方法相比，它具有不依赖于被控对象的精确数学模型，鲁棒性和适应性好，容易被操作人员接受等优点[2-3]。模糊控制有两种实现形式：一种是利用模糊规则修正PID控制参数的参数自整定PID控制器；另一种是直接通过模糊推理形成控制量的模糊控制器。

本文首先以模糊理论为基础分别设计了参数自整定PID控制器及模糊控制器；然后利用MATLAB构建俯仰-偏航联合控制回路仿真系统，在系统中存在控制耦合、随机干扰及模型参数时变的情况下对两种控制器的性能进行检验。由仿真结果可看出，参数自整定PID控制器更加符合悬浮火箭的控制需求。最后，对参数自整定PID控制器在悬浮火箭六自由度仿真模型中的控制性能进行验证。

1 两种控制器的设计

1.1 参数自整定PID控制器设计

基于模糊理论的参数自整定PID控制器的结构如图1所示[4]。

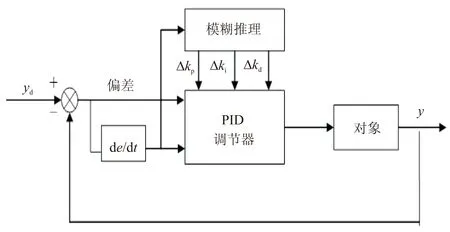
图 1 参数自整定PID控制器结构图Fig.1 Structure of parameter self-tuning PID controller

由图1可知，参数自整定PID控制器的输入是偏差e和偏差变化率ec，对输入量进行模糊化处理后根据规则进行模糊推理，得到输出Δkp、Δki和Δkd，将其分别输入PID调节器中，对PID参数进行实时在线整定。计算公式如下[5]

(1)

式中kp'、ki'、kd'为PID控制器的初始值。

PID控制器3个参数kp、ki、kd的在线模糊自整定应遵循如下规则[6-8]：

(1)当│e(t)│较大时，应取较大的kp，但不能过大；应取较小的kd，同时取消积分环节。

(2)当│e(t)│处于中等大小时，应取较小的kp，要恰当地选取kd，同时适当增加一点 。

(3)当│e(t)│较小时，应取较大的kp和ki，应取恰当的kd。

(4)当│ec(t)│较大时，kd可取得小些；当│ec(t)│较小时，kd可取得大些。

1.2 模糊控制器的设计

1.2.1 确定输入、输出变量及其模糊子集

选择Mamdani型模糊控制器，清晰化方法使用重心法。

控制器的输入是偏差e和偏差变化率ec，输出是控制量u。将输入变量e和ec的模糊论域取为[-1,1]，输出变量u的模糊论域取为[-2,2]。

输入变量取5个模糊子集，即{负大，负小，零，正小，正大}，可简记为{NB,NS,ZE,PS,PB}。各模糊子集的隶属度函数选为高斯型，其数学表达式如表1所示。

输出变量u同样取5个模糊子集，{NB,NS,ZE,PS,PB}。各模糊子集的隶属度函数选为高斯型，其数学表达式见表1。

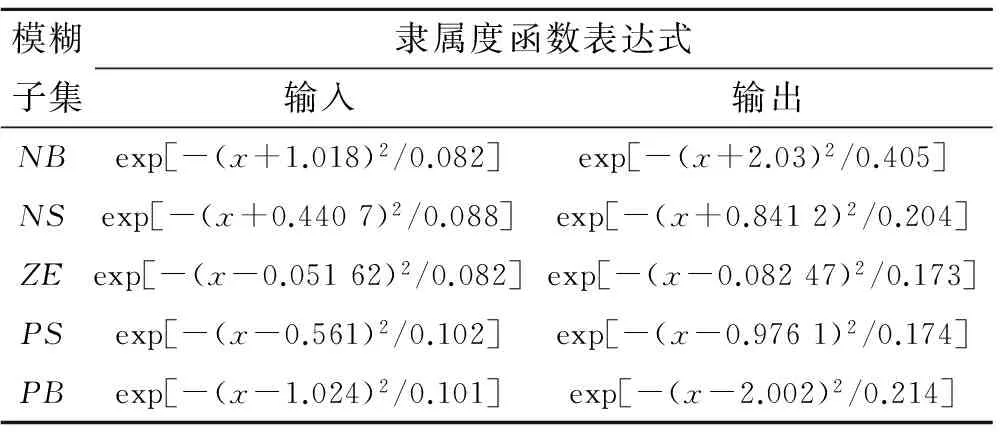
表 1 模糊控制器输入、输出变量隶属函数表Table 1 Membership function of input and output variable in fuzzy controller

1.2.2 确定模糊控制规则[9]

当偏差e为NB时，无论偏差率ec如何变化，控制量都应取为NB，以尽快减小误差。

当偏差e为NS时，如果ec为NB，会导致e向NB反方向变化，所以控制量应取为NB；如果ec为ZE或PS，则需要较小的控制量以帮助偏差e恢复至零，故取u为NS；如果ec为PS，则不需要控制量，取u为ZE。

当偏差e接近于零，即为ZE时，主要矛盾集中于稳定性，这时较小的控制量更加适合小幅度的调整。故ec为NB时，u取PS；ec为NS、ZE、PS时，u取ZE；ec为PB时，u取NS。

当偏差e为PS、PB时，可由上述规则对称得到，因此可总结出控制量u的模糊规则，如表2所示。

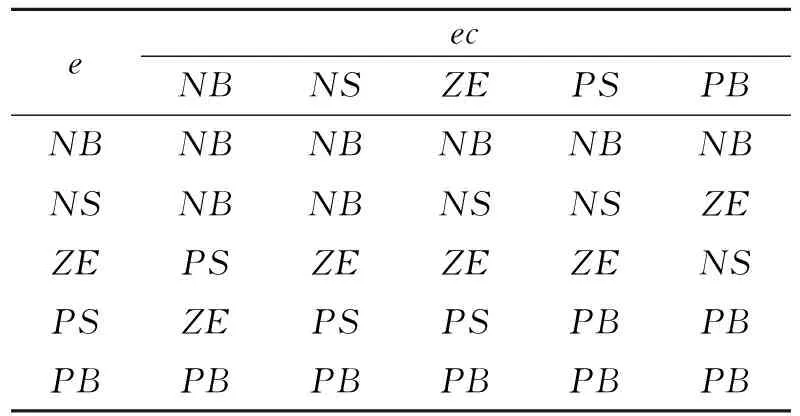
表 2 调节u的模糊规则表Table 2 Fuzzy control rules of u

2 仿真试验

2.1 俯仰-偏航联合控制回路仿真

在实际中，悬浮火箭的俯仰、偏航通道存在着控制耦合作用，耦合系数大小为10%～20%。同时，控制系统中还存在着随机干扰。因此俯仰-偏航联合控制回路模型如图2所示。

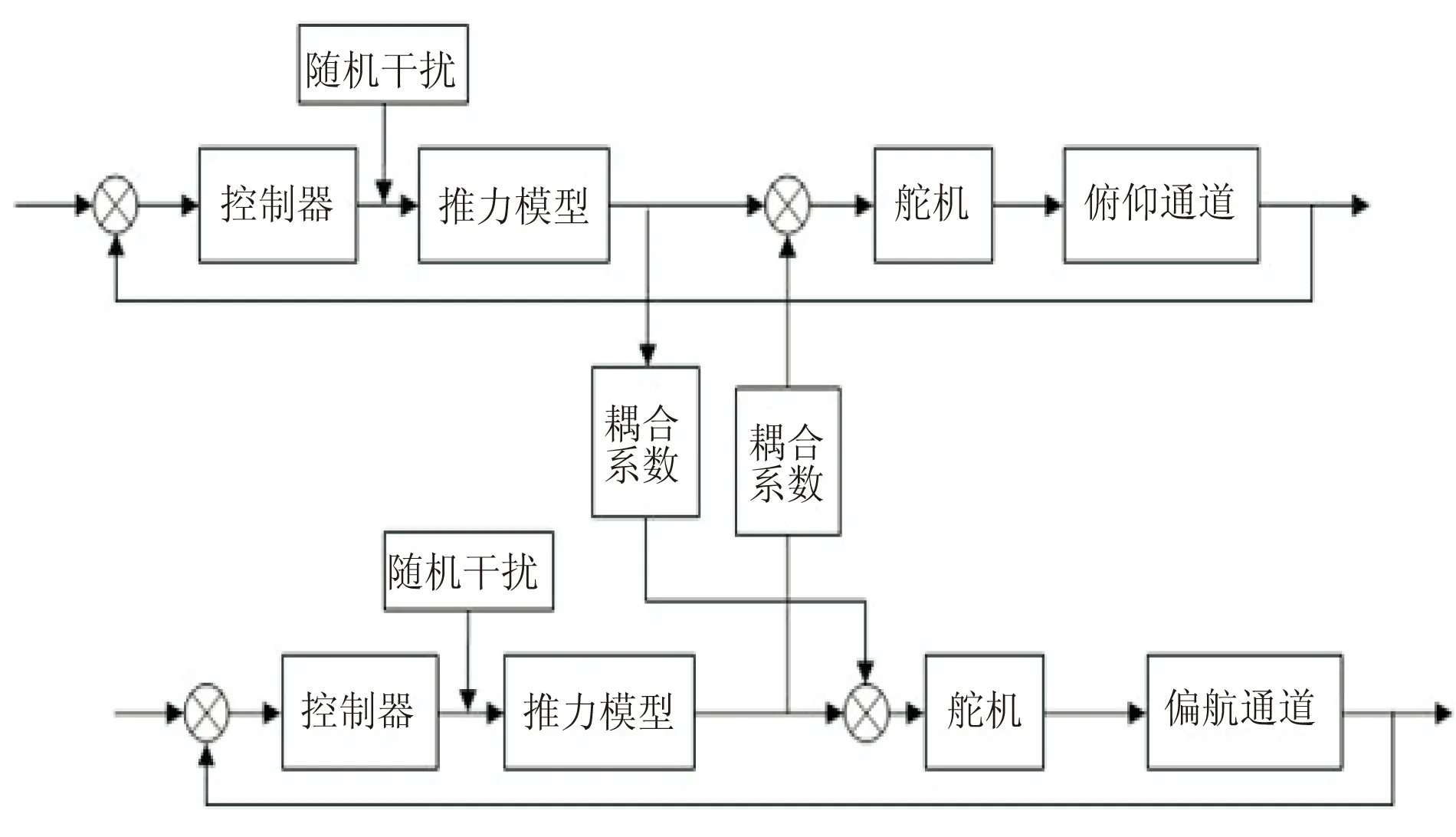
图 2 俯仰-偏航联合控制回路Fig.2 Joint control loop of yaw-pitch channel

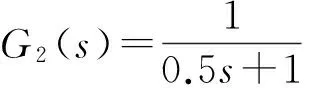
由于悬浮火箭的轴对称性，其俯仰、偏航通道模型一致：

其中，K2=1 280，K1=640，T3=24.2。而参数T2、T1、T0是随时间不断变化的。

利用MATLAB中的Simulink工具箱构建悬浮火箭的俯仰-偏航联合控制回路仿真系统。分别在仿真系统中验证参数自整定PID控制器及模糊控制器的控制性能。

如表3所示，选取5组参数，在耦合系数为20%时，加入如图3所示的随机干扰进行仿真。

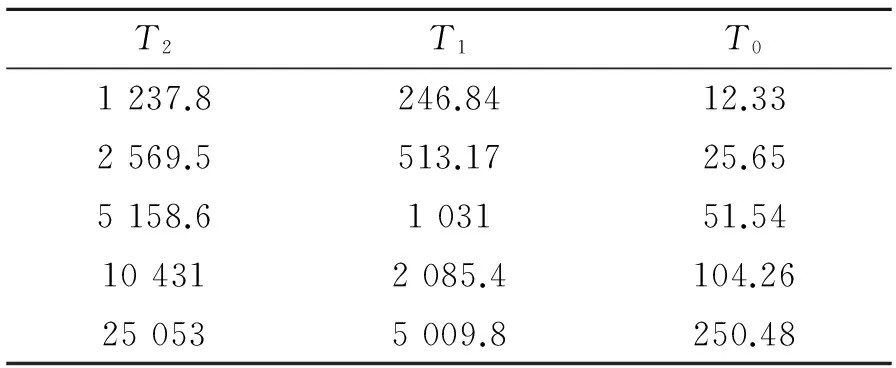
表 3 传递函数参数Table 3 Transfer function parameters

图 3 随机干扰Fig.3 Random interference

图4为传统PID控制器、模糊控制器、参数自整定PID控制器的5组阶跃响应。总结图4可得到3种控制器的阶跃响应动态性能如表4所示。

(a)传统PID控制器 (b)模糊控制器 (c)参数自整定PID控制器图 4 3种控制器阶跃响应Fig.4 Step response of three controllers

由表4可看出，文中利用模糊理论设计的2种控制器与传统PID控制器相比超调量明显降低，响应速度加快，调节时间缩短，控制性能有了明显提高。虽然当模型参数增大时，模糊控制器可较好地抑制系统超调，但调节时间也会随之增加，系统的响应减慢。而参数自整定PID控制器的阶跃响应则比较稳定，控制性能的变化很小。这说明参数自整定PID控制器具有较好的鲁棒性，能够抑制系统中存在的干扰作用，并且能适应参数时变系统，更加符合悬浮火箭的控制需求。

2.2 悬浮火箭六自由度仿真

如图5所示，利用Simulink搭建悬浮火箭的六自由度仿真模型。在初始俯仰角ϑ0=80°，初始偏航角ψ0=0°，初始滚转角γ0=5°，初始角速度ωx0=10(°)/s，ωz0=-10(°)/s的条件下，采用文中设计的参数自整定PID控制器进行悬浮火箭的六自由度仿真。

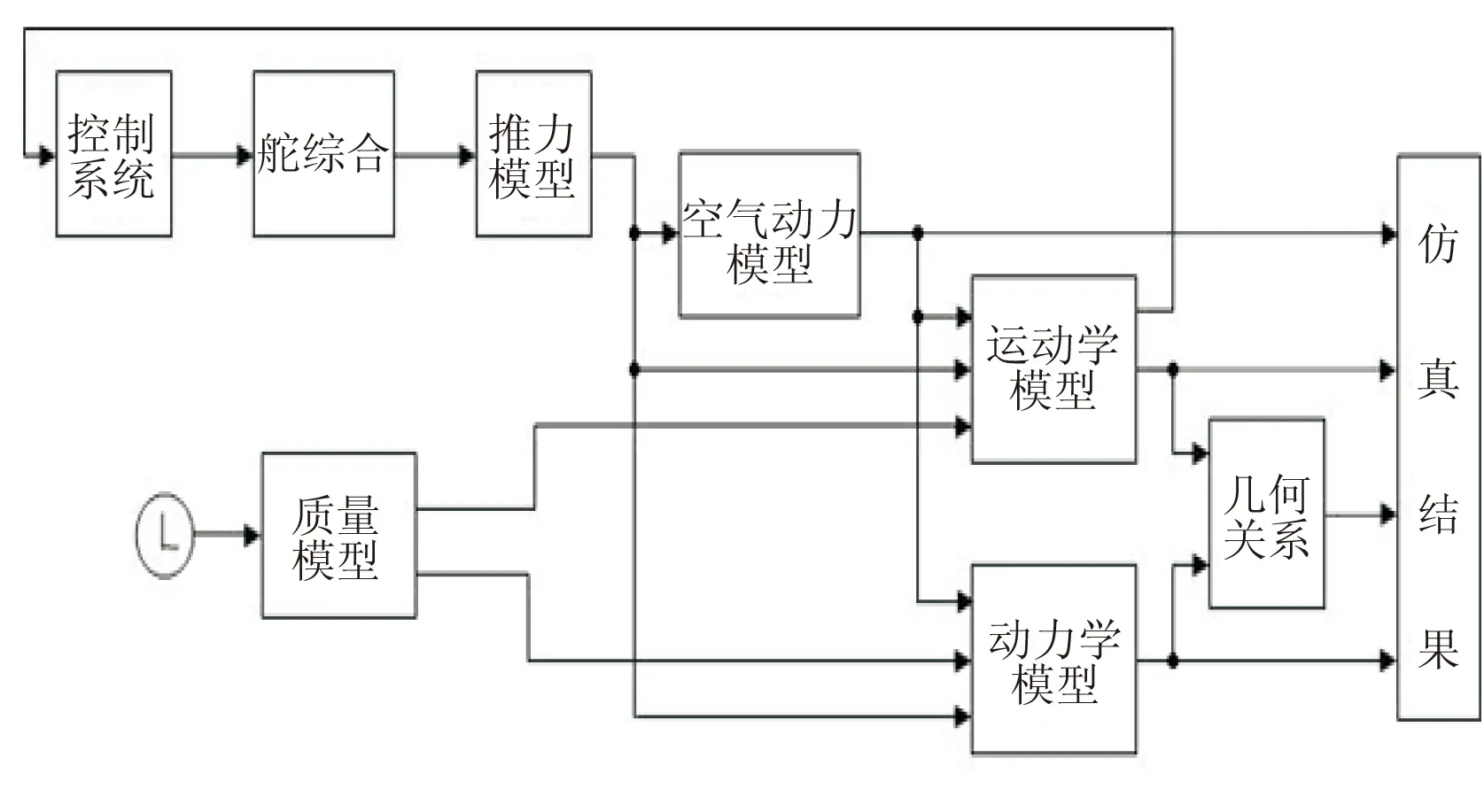
图 5 悬浮火箭六自由度仿真模型结构图Fig.5 6-DOF simulation model of suspended rocket

俯仰角仿真结果如图6所示。图6中虚线代表俯仰角指令，实线代表实际俯仰角。从图6可看出，由于初始偏差的干扰，在飞行初期，实际俯仰角与指令之间出现了最大3.08°的偏差。但在参数自整定PID控制器的作用下，误差在1.2 s内得到了纠正。并且在8 s后实际俯仰角与指令基本一致。这说明，在悬浮火箭的六自由度仿真中，参数自整定PID控制器能够快速抑制干扰，对指令信号的响应迅速，可获得优异的控制效果。

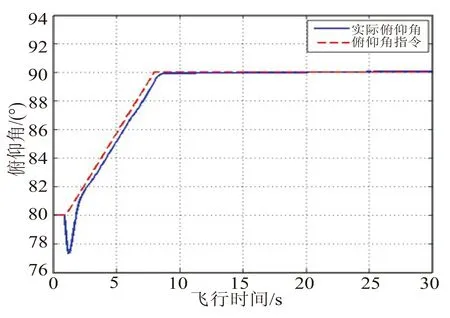
图 6 悬浮火箭俯仰角Fig.6 Pitch angle of suspended rocket

3 结论

(1)基于模糊理论设计了参数自整定PID控制器以及模糊控制器。与传统PID控制器相比，这两种控制器能够使系统性能得到明显提高。

(2)参数自整定PID具有较好的鲁棒性，能够抑制系统中存在的干扰作用，且能够适应参数时变的系统。与模糊控制器相比，控制性能更优，更加符合悬浮火箭的控制需求。

(3)参数自整定PID控制器在悬浮火箭的六自由度仿真中能够快速响应指令信号并抑制扰动，控制效果优异。

[1] 石长安,李为民,付强,等.舷外诱饵及其战术使用方式分析[J].飞航导弹, 2004 (11):59-62.

[2] 石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京：清华大学出版社；北京交通大学出版社, 2008:6-10.

[3] Eric Ting, Mohammad A Ayoubi. Optimizied fuzzy-proportional/integral/derivative controller for aircraft pitch control[J].Journal of Aerospace Information Systems,2013,10(8):414-429.

[4] 王辚,张科.基于MATLAB的自整定模糊PID控制系统[J].探测与控制学报,2008, 30(2):73-76.

[5] 焦仁雷,宋慧波,任亚宁,等. 模糊自适应PID控制系统的研究及MATLAB仿真[J].装备制造技术, 2015(2):87-89.

[6] 何鹏.基于Matlab的模糊PID控制器设计与仿真研究[J].微型电脑应用,2010,26(4):59; 62; 64; 69.

[7] 崇阳,李言俊,张科,等.基于DSP的模糊PID舵机控制算法设计与实现[J].飞行力学,2011, 29(2):86-88.

[8] 洪霖. 基于模糊PID策略的发动机调速控制研究[J].自动化技术与应用, 2015, 34(2):9-12.

[9] 石良臣. MATLAB/Simulink系统仿真超级学习手册[M]. 北京：人民邮电出版社, 2014:352-361.

(编辑：吕耀辉)

Design and simulation of suspended rocket controller based on fuzzy theory

HU Si-ao，YANG Jun，PAN Tao，CHEN Hua-bing

(The 41st Institute of the Fourth Academy of the CASC，Xi'an 710025，China)

Due to the control coupling in pitch and yaw channel caused by thrust vector control and the time varying parameters of the model, the traditional PID control algorithm cannot achieve an ideal control effect. In this paper, parameters self-tuning PID controller and fuzzy controller were designed based on fuzzy theory.A pitch-yaw joint control loop of suspended rocket was built by using MATLAB.The performance of the two controllers was verified under condition that 20% control coupling between the pitch and yaw channel and random noise were added to the simulation system. Time varying model was used in the simulation. As can be seen from the results, the parameters self-tuning PID controller has good robustness.The controller can suppress interference in the system. The performance of parameters self-tuning PID controller was verified in the 6-DOF simulation model of suspended rocket. Simulation result indicates that the suspended rocket can respond to the direction quickly.

fuzzy controller；parameter self-tuning；PID controller；suspended rocket

2015-09-20；

2016-02-03。

胡思翱(1991—)，女，硕士，研究方向为飞行器控制。E-mail：dearesth@126.com

V448

A

1006-2793(2016)06-0847-04

10.7673/j.issn.1006-2793.2016.06.019