高含硫气藏非均质试井解释模型研究
2017-01-04刘振平
刘振平
(中国石油新疆油田分公司勘探开发研究院,新疆克拉玛依834000)
高含硫气藏非均质试井解释模型研究
刘振平
(中国石油新疆油田分公司勘探开发研究院,新疆克拉玛依834000)
高含硫气藏在开采过程中,随地层压力不断下降,元素硫将以单体形式析出,从而堵塞天然气的渗流通道,降低地层有效孔隙空间及渗透率,影响气井的产能。针对高含硫气藏的特征,推导了地层中任一点的相对渗透率与距气井中心的径向距离之间的函数关系,并建立了高含硫气藏的非均质试井解释数学模型。然后,将模型在拉普拉斯空间的解经过解析反演后,与均质模型实空间的解进行对比分析。最后,利用Stehfest数值反演算法绘图验证了分析结果,并研究了试井分析理论曲线影响因素。研究结果表明,高含硫非均质试井解释模型能准确反映地层的渗流规律和解释地层的非均质性。元素硫在地层中的沉积具有“叠加效应”,并且随地层系数的减小,越易在地层中沉积。
高含硫气藏;硫沉积;非均质性;试井分析;拉普拉斯变换;解析反演
当天然气中的H2S达到一定的数值,在一定温度和压力下,元素硫会析出。地层中硫颗粒形成后,一部分随气流在多孔介质中运移,另一部分吸附沉积在孔喉表面,堵塞孔道,降低地层的孔隙度和渗透率[1]。严重时会发生“硫堵”,致使生产无法正常进行[2]。目前,对于硫沉积的研究大多侧重于沉积机理和预测模型的研究[3-6],而对气体在硫沉积地层中的渗流规律研究较少。而且,已有的研究都使用均质复合模型来描述高含硫气藏的渗流规律,物性在衔接面处呈阶梯变化[7-9]。
但是,实际生产中由于硫元素在地层中的沉积,地层的非均质性严重。Roberts[10]在1996年研究发现地层中某一点硫的沉积速度与该点距气井中心的径向距离的平方成反比。这说明硫的沉积对地层相对渗透率的影响是一个沿径向渐变的过程,存在过渡带。而均质复合模型中渗透率沿径向呈“台阶状”,在连接面处是突变的。因此,本文提出新的数学模型来描述高含硫气藏的非均质性,并用其建立了试井解释模型。
1 地层的相对渗透率分布
若地层中某一点硫的沉积速度与该点距气井中心的径向距离的平方成反比,则该点的气相相对渗透率满足:

式中:krg-气体相对渗透率;t-时间,s;b1-常数;r-地层中任一点距气井中心的径向距离,m。
设气井刚开始投产t=0时,krg=1,则对(1)式分离变量并积分得:

其中:b=b1t。
由式(2)可知,b是时间的函数,随着时间的持续而增大。高含硫气藏在开发早期,由于地层压力降低较小,元素硫析出沉积的量不多,此时地层渗透率下降并不明显。但到了开发的中后期,硫沉积达到一定规模后就将引起渗透率迅速降低,甚至堵塞孔道,使气井停产或报废。利用Roberts文中的数据计算某口气井的地层相对渗透率的分布(见图1)。
从图1可以看出,硫沉积对地层相对渗透率的影响沿径向的增大而逐渐减小,并不是突变的。并且,硫沉积对地层相对渗透率的影响主要集中在井筒附近,远井地带的地层渗透率变化并不明显。
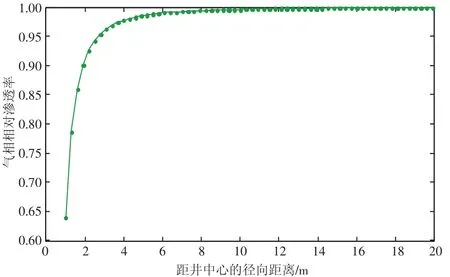
图1 气相相对渗透率沿径向的分布
2 高含硫气藏非均质试井解释数学模型
2.1 假设条件
(1)地层非均质,但各向同性,其渗透率为k(r),是径向半径r的函数;
(2)无限大边界等厚气藏,中心一口生产井以定产量q生产;
(3)考虑气体单相流体,在地层中渗流服从达西定律;
(4)考虑井筒储集效应和表皮效应,忽略重力和毛管力影响。
2.2 无因次数学模型
基于以上假设,可得高含硫气藏单井的非均质渗流模型。
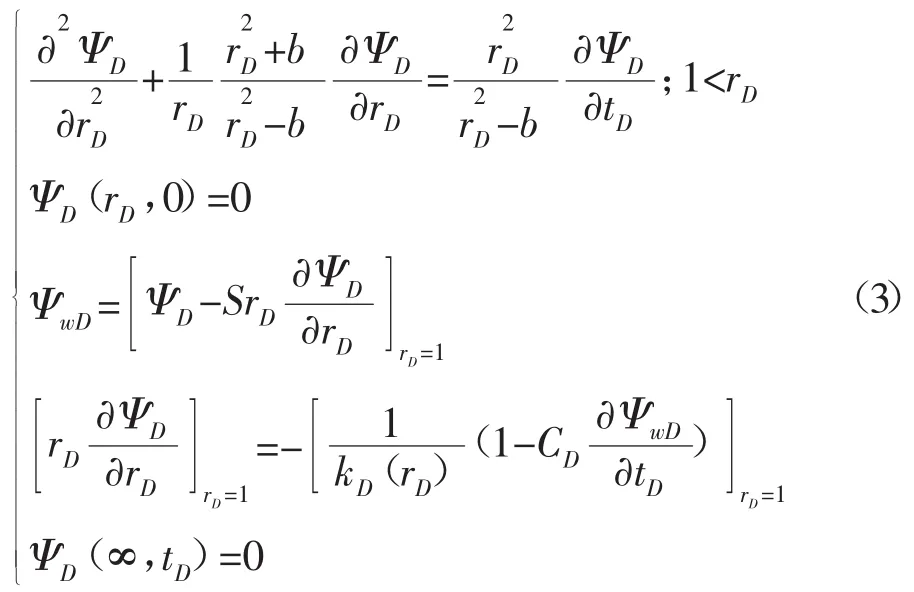
其中无因次变量定义如下:

式中:S-表皮系数,无量纲;ka-地层初始渗透率,mD;h-储层有效厚度,m;qg-产气量,104m3/d;T-地层温度,K;rw-井半径,m;Φ-储层孔隙度;Ct-综合压缩系数,MPa-1;μ-天然气黏度,mPa·s;t1-时间,h;C-井筒储集系数,m3/MPa;p-地层压力,MPa;Z-天然气压缩因子。
对(3)式进行Laplace变换,求解可得气井在无穷大边界条件下的无因次井底拟压力在拉普拉斯空间的解:
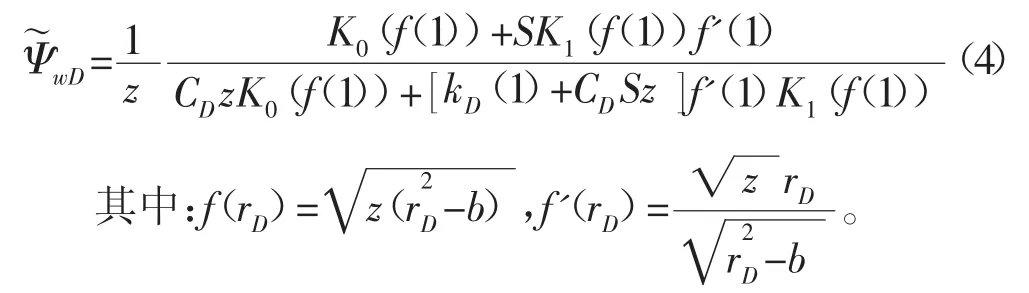
式中:z-拉普拉斯变量。
K0(x)、K1(x)-零阶、一阶第二类虚宗量贝塞尔函数。当b=0时,(4)式退化为均质模型的解,与李顺初、黄炳光[11]给出的解一致。显然,均质模型只是高含硫气藏非均质模型的一种特殊情况,而本文提出的高含硫非均质模型具有更普遍的适用性。
2.3 高含硫气藏非均质模型解的解析反演及对比分析
下面对(4)式解析反演,求出模型在实空间的解析解,并将结果与均质模型进行对比。
在早期,即z→∞,由Bessel函数的性质:

对(4)式进行化简和反演可得实空间解:

在晚期,即z→0,由Bessel函数的性质有:

则(4)式可化简为:
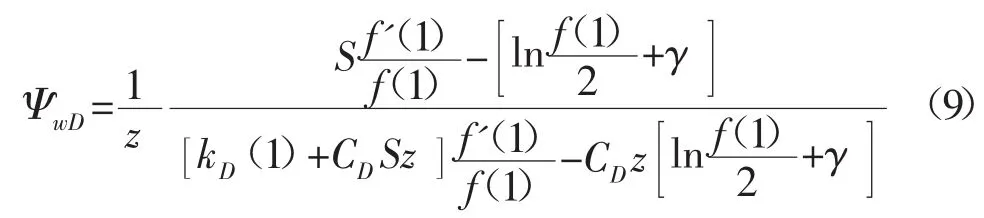
式中:γ-欧拉常数,取γ=0.577 2。
对式(9)进行解析反演和简化,可得径向流时无因次井底拟压力在实空间解:
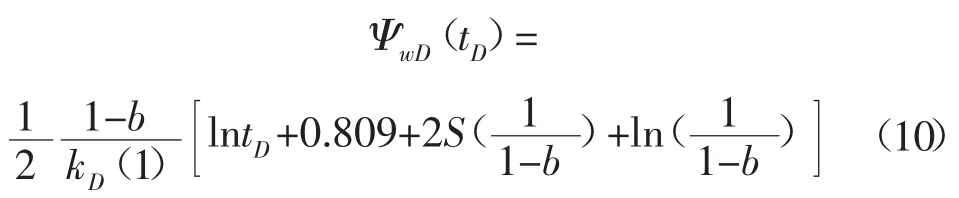
对(10)式两边关于lntD求导,得无因次井底拟压力导数:
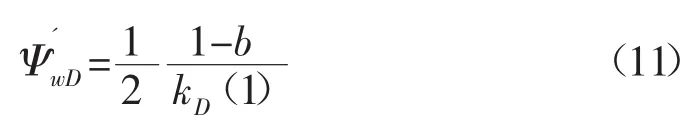
对于均质无限大气藏,李晓平等[13]给出无因次井底拟压力实空间解为:

观察(6)式和(12)式发现,在早期纯井筒储集阶段,高含硫气藏非均质模型和均质模型的解相同。对比(10)式和(13)式,在晚期由于硫沉积的影响,两者的解差别较大,但在形式上有一定的相似性。高含硫气藏非均质模型增加了考虑非均质性影响的变量,更能准确地反映地层的实际情况。
3 模拟验证及影响因素分析
3.1 模拟验证
根据(4)式,利用Stehfest数值反演算法,可以计算出高含硫气藏试井分析理论曲线,并与相同条件下的均质模型曲线进行对比(见图2)。
从图2上可以看出,在早期纯井筒储集阶段,高含硫气藏非均质模型和均质模型的曲线完全重合。这是因为此时仅存在井筒的续流效应,井底的压力响应并未反映出地层的特征。在纯井筒储集阶段结束后,二者的无因次拟压力和导数曲线都开始出现分离,并且高含硫非均质模型的曲线一直在均质模型曲线的上方。由于硫在地层中的沉积导致流体渗流阻力增大,高含硫气藏非均质模型的无因次拟压力曲线比均值模型的曲线高。在无限作用径向流阶段,高含硫气藏非均质模型的无因次拟压力导数曲线确实是一条大于0.5的水平线。这说明高含硫气藏非均质模型对硫沉积引起的非均质性更为敏感,无因次拟压力导数曲线偏离0.5水平线越多,地层的非均质性就越强。
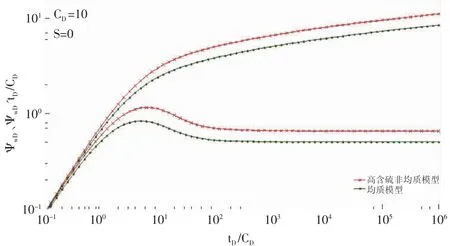
图2 高含硫气藏非均质模型与均质模型的对比图
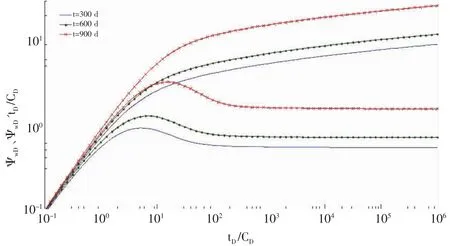
图3 生产时间t对试井分析理论曲线的影响
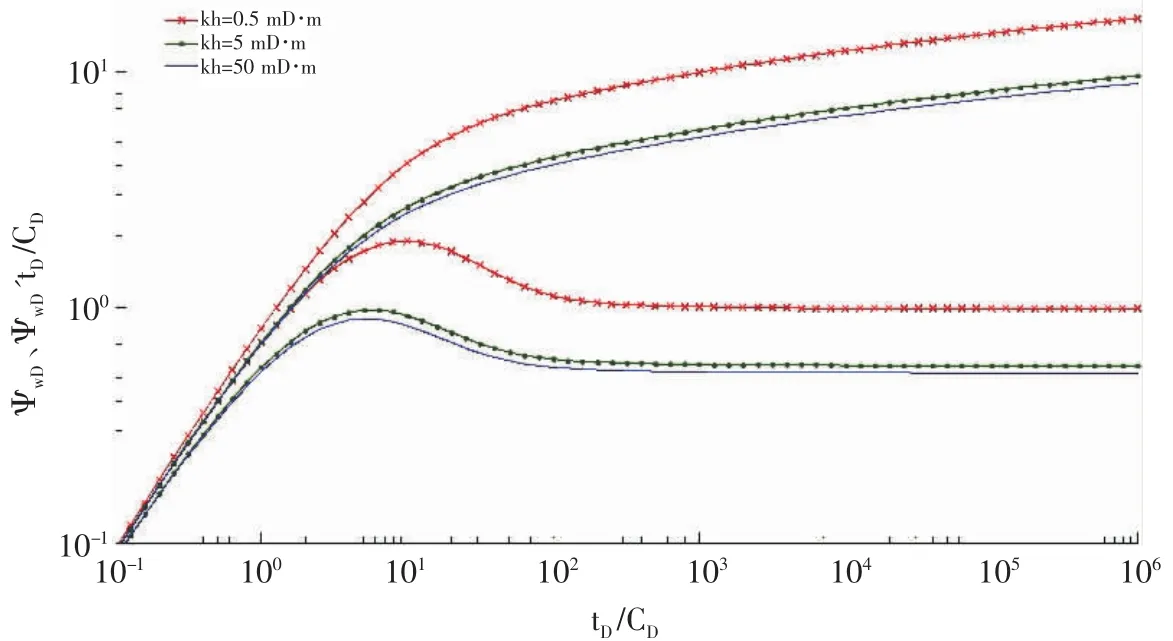
图4 地层系数kh对试井分析理论曲线的影响
3.2 影响因素分析
3.2.1 生产时间对试井曲线的影响(见图3)从图3可以看出在纯井筒储集效应结束后,随着生产时间t的增大,无因次拟压力和导数曲线会越来越高,硫沉积造成的渗流阻力越来越大。这说明硫的沉积会在地层中产生“叠加效应”,如果任由元素硫在地层中沉积,随着开发时间的延长,元素硫在地层中的沉积速度会加快,流体在地层中的渗流阻力会越来越大。因此,针对高含硫气藏,建议采取有关预防元素硫沉积危害的技术,如定期向井中加入硫溶剂,及时清除硫沉积造成的污染。
3.2.2 地层系数对试井曲线的影响(见图4)从图4可以看出在纯井筒储集效应结束后,地层系数越小,无因次拟压力和导数曲线就会越高,硫沉积造成的渗流阻力也就越大,说明硫沉积对低渗薄层气藏的影响更为严重。首先,因为低渗透气藏的渗流阻力大,气体流动速度较慢,元素硫更容易在地层中沉积。其次,由于产气层越薄,气体的渗流通道越少,对元素硫的沉积作用就越敏感。因此,对于低渗薄层高含硫气藏,射孔时应尽量整个气层全部射开,并尽早的采取措施,减少硫在地层中的沉积,防止“硫堵”的发生。
4 结论
(1)高含硫气藏的非均质试井解释模型能准确反映硫沉积气藏的渗流规律,均质模型仅是该模型的一种特殊情况。
(2)高含硫气藏非均质渗流模型在无限作用径向流阶段,无因次拟压力导数曲线是一条大于0.5的水平线。
(3)低渗薄层高含硫气藏更容易引起元素硫在地层的快速沉积,发生“硫堵”。
[1]胡书勇,张烈辉.高含硫气藏硫沉积的研究进展[J].钻采工艺,2009,32(1):71-74.
[2]欧成华,胡晓东,万红心.含硫气藏元素硫沉积及防治对策研究[J].钻采工艺,2005,28(6):86-89.
[3]付德奎,郭肖,杜志敏,等.高含硫气藏沉积机理研究[J].西南石油大学学报(自然科学版),2009,31(5):109-111.
[4]付德奎,郭肖,邓生辉.基于溶解度实验的高含硫非均质模型及应用研究[J].西南石油大学学报,2007,29(1):57-59.
[5]黄兰,孙雷,孙良田,等.高含硫气藏硫沉积预测模型和溶解度计算方法研究[J].重庆科技学院学报(自然科学版),2008,10(2):13-17.
[6]H.Mei,M.Zhang,X.Yang.The effect of sulfur deposition on gas deliverability[C].SPE 99700.
[7]李成勇,张烈辉,刘启国,等.高含硫气藏试井解释方法研究[J].钻采工艺,2006,29(1):51-53.
[8]刘永良,徐艳霞,徐艳梅,等.高含硫气藏产量递减模型研究[J].西南石油大学学报(自然科学版),2011,3(2):104-108.
[9]方晓春,蒋鑫,刘启国,等.高含硫气藏两区复合地层试井解释方法研究[J].重庆科技学院学报(自然科学版),2013,15(5):36-39.
[10]Bruce E.Roberts.The effect of sulfur deposition on gas well inflow performance[C].SPE 36707,1996.
[11]李顺初,黄炳光.拉普拉斯变换与Bessel函数及试井分析理论基础[M].北京:石油工业出版社,2000:176-199.
[12]吴明录,成珍,成绥民,等.非均质油藏试井分析新方法[J].油气井测试,2003,12(4):5-7.
[13]李晓平,张烈辉,刘启国.试井分析方法[M].北京:石油工业出版社,2009:60-61.
Study on anisotropic analytical model of well testing of high sulfur gas reservoir
LIU Zhenping
(Research Institute of Exploration and Development of PetroChina Xinjiang Oilfield Company,Karamay Xinjiang 834000,China)
During the exploitation of high sulfur gas reservoir,with the formation pressure declining,sulfur element will precipitate in the form of monomer,thus blocking flow matrix for natural gas,which cause severe reduction in the effective drainage porosity and permeability, affecting gas well productivity at last.For high sulfur gas reservoir characteristics,the functional relationship between relative formation permeability and radial distance of the well spacing has been derived.Further more,it has established a high sulfur gas reservoir anisotropy well testing analysis model.Then,comparative analysis the model solution in Laplace after space inversion parsed and solution in the real space model with homogeneous solution.Finally,drawings made by Stehfest numerical inversion algorithm method validated the analytical results,and further research on influence factors of the well test the theoretical curve.The results showed that the anisotropic analysis model of well testing can accurately reflect the formation percolation theory and interpret the extent of formation anisotropy.In the formation of elemental deposition has a"duplicate effect",and with the decrease of for-mation capacity,the more deposited in the formation.
high sulfur gas reservoir;sulfur deposition;anisotropy;well testing analysis;Laplace transform;analytic inversion
TE375
A
1673-5285(2016)12-0021-05
10.3969/j.issn.1673-5285.2016.12.006
2016-09-22
2016-10-11
刘振平,男(1990-),陕西渭南人,硕士,从事试井解释及油气藏开发方面的研究工作。
