西北荒漠区动植物关系定量探究

徐 路，朱家明，李美玲，程 刚

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

西北荒漠区动植物关系定量探究

徐 路1，朱家明2，李美玲1，程 刚1

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

针对西北荒漠区动植物关系的问题，进行线性回归分析，得出动植物生物量的变化趋势。然后通过相关性分析，得到不同干扰下动植物生物量之间的变化关系。最后使用多元统计方法处理数据，使用均匀系数计算和可行性检验，分别构建植物高度、盖度和密度对啮齿动物稳定性影响模型，不同干扰对啮齿动物群落影响模型，从而揭示不同干扰对啮齿动物群落的影响机制，可为我国荒漠区生态环境的保护和治理提供参考。

动植物相关性；回归分析；均匀系数；可行性检验；MATLAB；EVIEWS

0 引言

随着现代化的发展和社会科学技术的进步，人类活动的不断加剧，使得荒漠化现象愈发突出，已经成为当今全球主要的生态环境问题之一，而荒漠化在我国的生态环境问题之中是涉及当下以至未来的重点问题，土地荒漠化不仅危害到了生物生存的生态环境，影响生物多样性，而且威胁到了人类赖以生存的自然资源环境和社会经济的持续发展。西北干旱区是我国典型的荒漠化地区，降水量极少，蒸发量极大，且地貌也显现出风化特性，它独特的自然地理特征决定了它生态系统十分脆弱，而这样的脆弱的生态系统一旦被破坏，其本就不平衡的自然环境将会迅速退化甚至崩溃。所以，了解荒漠干旱区生态系统在不同干扰模式下植物地上生物量，啮齿动物生物量的变化趋势，揭示两者之间的变化关系，并对啮齿动物群落稳定性展开研究，发现干扰对于啮齿动物群落的影响机制，可为我国治理干旱区生态系统提供有效的建议。

1 数据的获取及假设

数据来源于2015年第八届“认证杯”数学建模网络赛C题[1]。为了便于解决问题，提出以下假设：1)过牧区和轮牧区土壤PH植保持不变；2)光照对于牧区植物动物影响很小，可以忽略；3)不考虑一个月内的时间变化因素；4)测试所取的土地面积无差异；5)忽略瘟疫、地震等突发灾害对物种的多样性的偶然影响。

2 不同干扰下植物和啮齿动物生物量的变化趋势

2.1 不同干扰下植物生物量的变化趋势

利用控制变量法，首先温度(月份)不变，得过牧区植物生物量与轮牧区植物生物量的相关关系与变化；然后人类活动(牧区)不变，得7月份植物生物量与10月份植物生物量的相关关系与变化。根据以上两者的相关关系与变化，得出不同干扰因素下、植物生物量的变化趋势。

(1)不同非生物因子下植物群落生物量变动趋势。

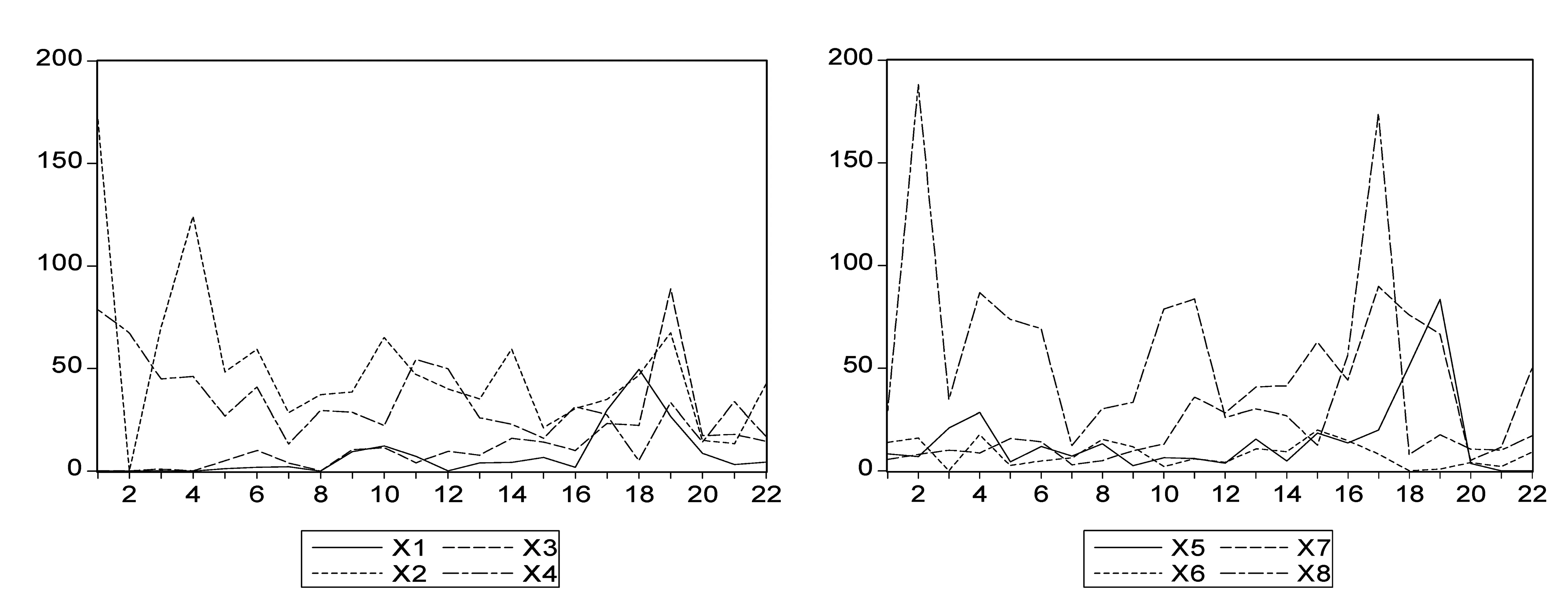
图1 7月份和10月份草本和灌木在不同区域生物量的变动趋势

(2)分析不同人为干扰因子下植物群落生物量的变动趋势。

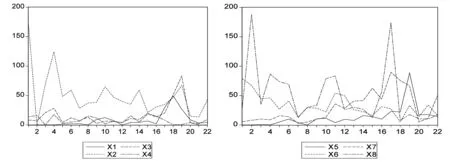
图2 过牧区和轮牧区不同月份植物群落地上生物量的变动趋势

(3) 最后，建立植物因子对于植物生物量的影响模型，并进行相应检验。经过多次尝试，最终决定建立倒数变换模型(双曲线函数模型)，7月份草本植物在过牧区不同生物因子与生物量关系的函数：

其中，y1为7月份草本过牧区生物量；x1、x2、x3分别表示7月份草本过牧区的高度、盖度、密度。计算结果表明：在假定其他变量不变的情况下，高度每增加1单位，草本植物生物量减少1/0.0832，盖度每增加1单位，草本植物生物量增加 1/0.2042，密度每增加1单位，草本植物生物量增加1/52.6780。即：草本生物量与高度呈负方向变动，回归系数为12.1092，变动幅度明显，随着高度的变动，植物群落地上生物量变动幅度明显；与盖度呈正方向变动，回归系数为4.8972，随着盖度的变动，植物群落地上生物量变动幅度较为明显；与密度正方向变动，回归系数为0.0190，变化幅度不明显，随着密度的变动，植物群落地上生物量变动幅度很小。

通过前面的分析，综合对各个模型进行不同的多元回归分析见下表：

表1 各个模型进行不同的多元回归分析数据

综合分析：根据对以上数据以及结果的分析，对于总的植物生物量而言，过牧区7月份的植物生物量大于10月份的植物生物量；而在轮牧区中，7月份的植物生物量却小于10月份的植物生物量。

2.2 不同干扰下啮齿动物生物量变动趋势

(1) 过牧区不同月份啮齿动物优势种百夹捕获率：

在过牧区，7月份不同的啮齿动物种群的变化幅度几乎一致，其捕获率小毛足鼠>子午沙鼠>三趾跳鼠；在10月份不同的啮齿动物种群存在差异，其中三趾跳鼠与子午沙鼠的捕获率高，且变化幅度明显。

(2)轮牧区不同月份啮齿动物优势种百夹捕获率：

轮牧区，7月三种优势种的捕获率变动存在明显的差异，子午沙鼠的捕获率较高，且变动幅度大，而小毛足鼠与三趾跳鼠的捕获率很低，且变化幅度不明显；10月份优势种的变化幅度大致相同，其捕获率子午沙鼠>小毛足鼠>三趾跳鼠。

综合所述，不同的啮齿动物种群在不同的干扰下，其生物量的变化趋势存在明显的差异，子午沙鼠在不同的干扰下其生物量较高，小毛足鼠在过牧区7月份生物量较高，三趾跳鼠在过牧区10月份生物量较高。而对于总的啮齿动物生物量而言，过牧区之中，7月份的啮齿动物生物量高于10月份的啮齿动物生物量。

2.3 植物生物量和啮齿动物生物量相关变化模型

分析植物生物量以及动物生物量共同在人为因素以及自然因素的干扰下所做出的相同或不同反映或变化。然后，对于植物生物量以及动物生物量两者变化之间的关系进行观察研究，讨论植物生物量变化对动物生物量变化的影响以及动物生物量变化对植物生物量变化的影响。

对植物生物量和啮齿动物生物量进行相关性分析：

表2 植物生物量和啮齿动物生物量进行相关性分析表

由上表植物生物量和啮齿动物生物量的相关系数为-0.255，植物生物量标准化数值x和啮齿动物生物量标准化数值y大体呈负相关。

3 啮齿动物群落稳定性研究

对于不同的啮齿动物优势种百夹捕获率，在22次的重复下，对于不同的人为干扰因子，求出7月和10月(代表夏季与秋季)的百夹捕获率总和，再求各种群生物量捕获率在该月总捕获率中占的比例，利用Pielou均匀性指数计算得出夏季与秋季啮齿动物群落生物量的均匀性值。进行啮齿动物群落生物量在不同干扰因子下的均匀性研究，建立均匀指数模型。

其中：Pielou的均匀度指数计算公式为：

J=(—∑Pi*ln(Pi))/lnS

式中S为百夹捕获率总和，Pi表示每一种啮齿动物在不同干扰下的捕获率占其总捕获率的比例。

计算不同干扰方式下啮齿动物群落捕获率均匀性值，如表3所示。

表3 不同干扰方式下啮齿动物群落捕获率均匀性值

由表3可知，啮齿动物群落生物量的月份(季节)均匀性在不同人为干扰因子下的变动不同。啮齿动物群落生物量在过牧区均值为0.56～0.70之间，变化幅度大，7月(夏季)低于10月(秋季)；在轮牧区均值为0.50～0.86，变化幅度大，7月(夏季)高于10月(秋季)，在轮牧区对于不同的种群存在明显的差异，三趾跳鼠的均匀性值明显大于子午沙鼠，而小毛足鼠的数据存在较大误差，因此无法比较。通过啮齿动物群落生物量均匀性指数的比较分析说明，不同干扰方式对啮齿动物群落生物量产生了明显不同的作用，其中主要是在夏季的轮牧区以及秋季的过牧区啮齿动物群落生物量均匀性指数较高，而在过牧区夏季处于较低的水平。

4 动物群落对不同干扰类型的敏感性的多元回归模型

对于动物群落对不同干扰类型的敏感性研究，建立相应的多元回归模，并进行残差分析。通过MATLAB软件，分析在过牧区10月份草本植物的高度、盖度、密度对三种啮齿优势种捕获率总和的影响，建立多元回归模型。对数据进行残差分析，结果如图3所示。

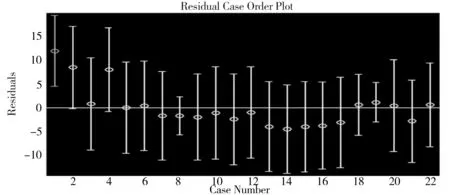
图3 10月份草本植物的高、盖、密对三种啮齿优势种捕获率总和的影响多元回归残差分析

由图3得出，第一组数据偏离较大，因此剔除第一组数据后，对高度、盖度、密度和三种啮齿优势种捕获率总和建立多元回归模型：

y=6.7391-0.5808x1-0.0967x2+0.0026x3

其中，y为三种啮齿优势种捕获率总和；x1、x2、x3分别为高度，盖度，密度。在过牧区10月份草本植物啮齿动物生物量与高度呈负相关，与盖度呈负相关，与密度呈正相关。通过MATLAB软件，分析在过牧区10月份灌木植物的高度、盖度、密度对三种啮齿优势种捕获率总和的影响，建立多元回归模型。对数据进行残差分析，结果如图4所示。

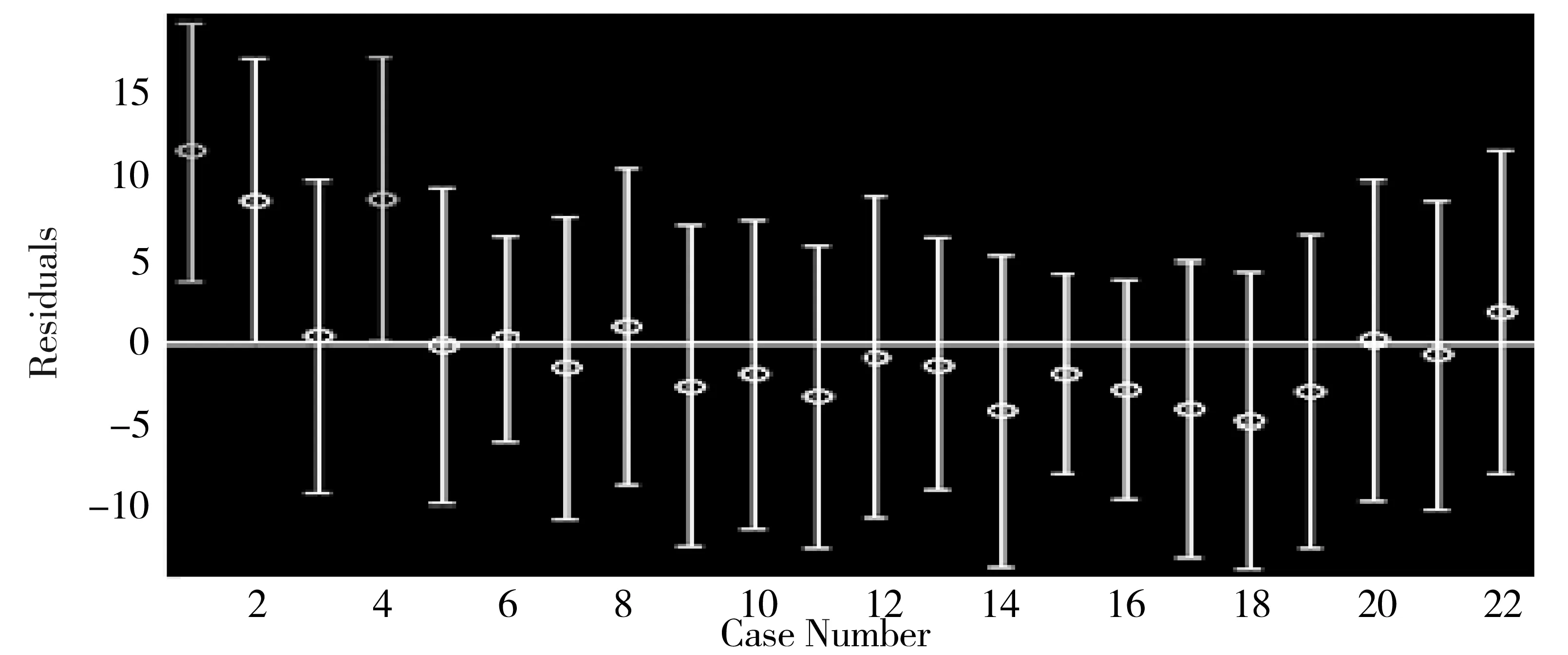
图4 10月份灌木植物的高、盖、密对三种啮齿优势种捕获率总和的多元回归残差分析

由图4得出，第一组、第四组数据偏离较大，因此剔除该数据后，对高度、盖度、密度和三种啮齿优势种捕获率总和建立多元回归模型：

y=6.0378+0.0088x4-0.0756x5-0.3922x6

其中，y为三种啮齿优势种捕获率总和；x4、x5、x6分别为高度，盖度，密度。通过模型的分析，在过牧区10月份草本植物啮齿动物生物量与高度呈正相关，与盖度呈负相关，与密度呈负相关。

5 结论和建议

首先通过建模分析出荒漠区不同干扰下植物地上生物量、啮齿动物生物量的变化趋势, 其次揭示了不同干扰下植物生物量与啮齿动物生物量之间的变化关系，最终通过对啮齿动物群落稳定性的研究, 揭示出干扰对于啮齿动物群落的影响机制。以下是本次研究的重要结论：

(1)不同干扰下，对植物生物量的影响。

在人类活动不变(即为牧区)的情况下，求出7月份植物生物量与10月份植物生物量的相关关系与变化：对于总的植物生物量而言，过牧区7月份的植物生物量大于10月份的植物生物量；而在轮牧区中，7月份的植物生物量却小于10月份的植物生物量。

在温度不变(即为月份)的情况下，求出过牧区植物生物量与轮牧区植物生物量的相关关系与变化：轮牧区植物生物量小于过牧区植物生物量。所以，西北干旱区应该提高植被总量，有利于植物的恢复力稳定性，为了保持资源的可持续利用，人类应该减少过牧区，增加轮牧区。轮牧区是草地采取围栏轮牧的利用方式，轮牧区对土地的不断循环利用较好，而过牧区是过度放牧利于方式，容易造成土地沙化。

(2)不同干扰下，对啮齿动物生物量的影响。

不同的啮齿动物种群在不同的干扰下，其生物量的变化趋势存在明显的差异，子午沙鼠在不同的干扰下其生物量较高，小毛足鼠在过牧区7月份生物量较高，三趾跳鼠在过牧区10月份生物量较高。而对于总的啮齿动物生物量而言，7月份的啮齿动物生物量高于10月份的啮齿动物生物量。所以，由于几乎所有的啮齿目动物都以植物为食,尤其是以种子为食，啮齿动物数量大不利于放牧，在食物链上，啮齿动物会和牛羊是竞争者，所以人们在不同牧区放牧时，要考虑啮齿动物放牧的影响，把啮齿动物的数量控制在有效的范围内，群落之间形成相对稳定的状态。

(3)植物生物量和啮齿动物生物量之间的关系。

再将动物生物量与植物生物量建立关系，得出动物生物量与植物生物量大呈较弱的负相关。所以，动物与植物数量保持一定的稳定性，有利于两者协调生存。

因此,合理放牧成为一个重大问题。合理放牧使得优势鼠种与草本、灌木达到一个平衡状态，使生态系统得以稳固。积极开展和深化干旱区的生态学研究,对于该区域的经济发展与生态环境保护具有深远的理论意义与实践价值。为该地制定农田小型啮齿动物区域性综合治理措施提供主要依据，对指导该地区农田害鼠的监测与防控，确保粮食生产安全等具有重要意义，采用以天然恢复为主的人工治理与天然恢复相结合措施进行生态环境建设。

[1] 2015年第八届“认证杯”数学中国数学建模网络挑战赛C题[EB/OL]．http://www．tzmcm．cn/．

[2] 周道玮，钟秀丽．干扰生态理论的基本概念和扰动生态学理论框架[J]．东北师大学报，自然科学版，1996，28(1)：90-96．

[3] 王利清．不同干扰方式对荒漠植物与啮齿动物群落的作用[J]．内蒙古农业大学学报，2006，27(3)．

[4] 张福顺．不同干扰下荒漠啮齿动物群落格局动态及其敏感性研究[D]．内蒙古农业大学，2005．

[5] 杨桂元，朱家明．数学建模竞赛优秀论文评析[M]．合肥:中国科学技术大学出版社，2013．

[责任编辑：崔海瑛]

Quantitative relationship between explore northwest desert plants and animals

XULu1,ZHUJia-ming2,LIMei-ling1,CHENGGang1

(1.SchoolofFinance,AnhuiUniversityofFinanceandEconomics,Bengbu233030,China;2.SchoolofStatisticsandAppl.Math,AnhuiUniversityofFinanceandEconomics,Bengbu233030,China)

According to the problem of the relationship between animals and plants in the desert area, the linear regression analysis was carried out, and the change trend of the plant biomass was obtained. And then, the relationship between the different disturbance of plant biomass was obtained by correlation analysis. Finally multivariate statistical method of data processing, respectively, using uniform coefficient calculation and the feasibility test, plant height, coverage and density effect on the stability of the rodent model are built up respectively, different interference effects on the rodent community model so as to reveal the influence mechanism of different disturbance of rodent community, provide a reference for the protection and management of the ecological environment in the desert area in China.

Animals and plants; Regression analysis; Uniformity coefficient; Feasibility test; MATLAB; EVIEWS

朱家明(1973-)，男，安徽泗县人，副教授，从事应用数学与数学建模方面研究。

国家自然科学基金资助项目(11301001)；安徽财经大学教研项目(acjyzd201429)。

Q

A

DOI10.13356/j.cnki.jdnu.2095-0063.2016.06.014