概率分析微信群抢红包的本质
2017-01-04刘洋
刘 洋
(大庆师范学院 教师教育学院,黑龙江 大庆 163712)
概率分析微信群抢红包的本质
刘 洋
(大庆师范学院 教师教育学院,黑龙江 大庆 163712)
随着手机网络的普遍应用,微信群抢红包大肆流行,甚至愈演愈烈,直至犯罪。概率是研究随机现象统计规律的一门学科,数学期望是随机变量的重要数字特征之一,在量化获利方面有着重要的意义。首先介绍了几种较为流行的微信群抢红包玩法,接下来利用古典概型,条件概率及概率的性质等概率知识对最小金额红包接龙玩法进行分析,然后通过数学期望揭示微信群抢红包的本质。
概率;数学期望;条件概率;微信群抢红包;本质
0 引言
微信群抢红包是一种大众化的娱乐方式,已成为人们传递情感,分享喜悦的一种不可缺少的手段。微信群红包一般有两种,一是普通等额红包,二是拼手气群红包。由于拼手气群红包的随机性、隐蔽性和开放性等特点,给别有用心的人提供了平台和工具,微信群抢红包犯罪事件频频浮出水面,涉案人数众多,金额庞大。那么在拼手气抢红包的微信群中,群成员到底能不能获利,微信群抢红包的本质又是什么,本文根据拼手气群红包的随机性等特点,利用概率知识揭示微信群抢红包的本质。概率起源于博弈,是研究随机现象统计规律的学科,在日常生活中应用十分广泛。比如说,在工业生产中用来检验产品的次品率;在车间包装线上用均值来掌控净重;在投资决策中用期望量化获利,用方差评估风险;在城市交通中也被用来合理规划路线[1];在抽奖活动中用来揭示其本质等等。
1 微信群抢红包的玩法
1.1 最少金额红包接龙
最少金额红包接龙大致有两种方式:
方式一:群主建立一个拼手气微信抢红包群,按此规则接龙:若群里有四人及以上成员同时响应,群主开始发一个启动红包,金额500元分四个包给群成员(不包括群主)抢,抢到金额最少的成员给群主发一个500元的红包,群主从中抽取10%,剩下金额分四个包发到群里给群成员(不包括群主)抢。
方式二:按此规则接龙:若群里有四人及以上成员同时响应,群主开始发一个启动红包,金额500元分四个包发到群里大家抢,抢到金额最少的成员以同样的方式发下一个红包,如果群主抢到金额最少的红包,由抢到金额倒数第二少的群成员发红包。
1.2 尾数最小红包接龙
群主建立一个“128元分四包,少发一分退群”的拼手气微信红包群,定下抢红包规则:由群里代包手先发128元分四个包给大家抢,抢到的红包尾数最小者,要以扫码的方式发给代包手128元的红包,代包手从中抽走20元后,将剩下的108元红包以同样的方式发回群里。每个红包抽走的20元分成两部分:10元是群主和代包手分成费;还有10元放在微信群奖金池里,用来调动群成员的积极性。
1.3 提前下注猜红包尾数
群主建立一个微信抢红包群,规定以第二个抢到的红包尾数作为随机开奖号码,群成员在开奖前私信找群主押注,买中大小和单双均为两倍,买中数字为六倍。每注可押20元到500元不等。只要猜中大小、单双或者数字,就可以获得倍数不等的收益,反之,押注统统不退还。
微信群抢红包的玩法仍在不停地发生改变,群主的盈利是显而易见的,特别是红包接龙玩法。参与的群成员认为微信抢红包是公平的,因为在抢红包结束后结果才能确定,之前的随机性是无法预测的,因此微信抢红包时只要运气好是可以获利的。事实是什么呢?下面针对最少金额红包接龙方式一进行分析。
2 微信群抢红包的本质
微信群抢红包之所以受大家欢迎,除了展示运气好以外,更重要的原因是大家觉得在微信群抢红包的过程中可以获利。但是由于微信群抢红包具有随机性,红包的分配金额及抢到红包的人都是不确定的,所以参与者的获利情况是不确定的。为此,引入随机变量,利用随机变量的数学期望量化参与者每轮抢红包的获利,然后根据数学期望的可加性分析参与者的获利。
2.1 建立数学模型
为了研究方便首先假定微信红包群有11人,群主1人,群成员10人。排除作弊器等外在人为因素,并作如下模型假设:
1) 假设每轮抢红包群成员间彼此独立;
2) 假设每轮抢红包时不响应成员不抢红包,且每位成员是否响应是等可能的;
3) 忽略群主的启动红包;
4) 假设每轮四个红包的分配金额分别为a元,b元,c元,d元,其中d为最小值,并且a+b+c+d=450;
5) 规定从群主发红包到抢到金额最少的成员给群主发红包为一轮。
在上述模型假设下,最少金额红包接龙方式一可以变为如下概率问题:
四个装有a元,b元,c元,d元的微信红包,随机的分配给十个互不相干的人(小王为其中一员),在四人及以上成员响应的条件下,讨论小王每轮的获利情况。
2.2 模型求解
记X表示小王每轮抢到的红包钱数,Y表示小王每轮获利的钱数,Z表示每轮抢红包时响应的人数,
根据接龙规则及模型假设,随机变量X的所有取值为a,b,c,d,0,根据条件概率的定义[2]可知

由概率的有限可加性[3]得

根据模型假设1)与2)易得随机变量Z的分布,
Z~B(10,0.5)
于是

又因为
P{X=a;Z=i}=P{X=a;小王以及其余(i-1)人同时响应},
记小王以及其余(i-1)人同时响应为事件A,则
P{X=a;Z=i}=P{X=a;A}
=P(A)P{X=a|A}


综上随机变量X的分布列为
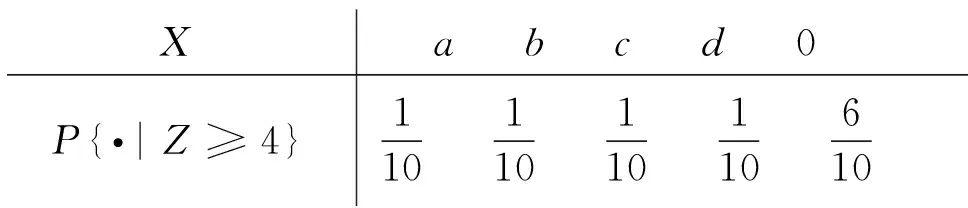
X a b c d 0P{·|Z≥4}110 110 110 110 610
根据随机变量Y与随机变量X的关系,易得随机变量Y的分布列,
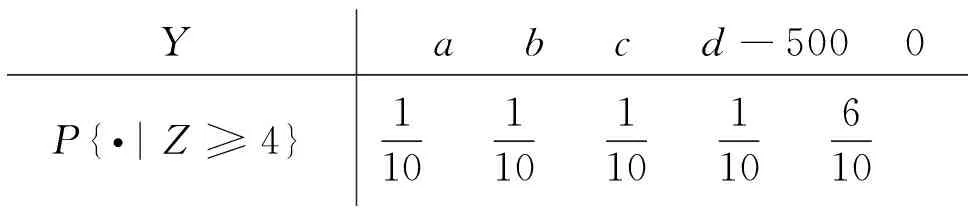
Y a b c d-500 0P{·|Z≥4}110 110 110 110 610
根据离散型随机变量数学期望的定义[3]得
从结果来看,小王每轮获利的钱数期望值为-5。尽管每轮小王抢到红包金额最少的概率为0.1,比较小,但是每轮抢到红包不用发红包的概率也不大,只有0.3。并且从平均意义上来看,小王平均每轮陪-5元。因此,在最小金额红包接龙方式一的规则下群成员不会获利,不仅如此,玩的越久输的越多。如果群主不从中抽红,可以看到EY=0,此时就是所谓的零和游戏。
3 总 结
本文首先阐述了当下较为流行的微信群抢红包的玩法,然后利用概率知识分析了最少金额红包接龙方式一。通过恰当的模型假设,引入离散型随机变量X,Y,Z,进而求得随机变量X,Y的分布列,然后利用数学期望量化获利,揭示微信群抢红包的本质,群成员不会获利,玩的越久,输的越多。微信群抢红包作为一种娱乐方式是可以接受的,但是大家不要沉迷其中,更不要参与上述抢红包的微信群,远离赌博,小心红包陷进!
[1] 朱耀兵,宋城.城市平面交叉可靠性分析[J]. 中国城市交通,2010(1):31-32.
[2] 李贤平.概率论基础[M].北京:高等教育出版社,2005:56-59.
[3] 李晓明,谢祥俊,刘建兴.概率论与数理统计[M].高等教育出版社,2010.
[责任编辑:崔海瑛]
刘洋(1985-),女,黑龙江大庆人,讲师,从事多元统计分析研究。
A
DOI10.13356/j.cnki.jdnu.2095-0063.2016.06.013
