概率论中关于标准正态随机变量乘积的探究
2017-01-04王蓉华徐晓岭顾蓓青雷平
王蓉华,徐晓岭,顾蓓青,雷平
(1.上海师范大学 数理学院,上海 200234;2.上海对外经贸大学 商务信息学院,上海 201620)
概率论中关于标准正态随机变量乘积的探究
王蓉华1,徐晓岭2,顾蓓青2,雷平2
(1.上海师范大学 数理学院,上海 200234;2.上海对外经贸大学 商务信息学院,上海 201620)

标准正态分布;分布函数;密度函数;随机变量的乘积
1 引言

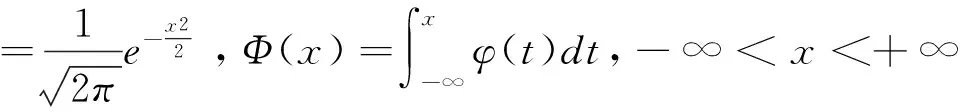
2 两个标准正态随机变量乘积的分布




所以X1+X2,X1-X2相互独立,进而有Y1,Y2相互独立。
又
对y≤0,
FY(y)=P(Y≤y)=P(Y1-Y2≤2y)
对y>0,
FY(y)=P(Y≤y)=P(Y1-Y2≤2y)

(方法二)对y≤0,
FY(y)=P(Y≤y)=P(X1X2≤y)
对y>0,FY(y)=P(Y≤y)=P(X1X2≤y)=P(X1X2≤0)+P(0 下面验证方法一与方法二的结果是一样的,即要验证如下等式成立: 定理2:设总体X~N(0,1),Y~N(0,1),且相互独立,而X1,X2和Y1,Y2是分别来自总体X,Y的容量为2的一个简单随机样本。记Z=X1Y1+X2Y2,则Z的密度函数为: 证明:注意到 即矩阵A是正交阵,也即上述线性变换为正交变换。 则 又 进而得Z的密度函数为: 则 又Y1,Y2,X1,X2的联合密度函数为:fY1,Y2,X1,X2(y1,y2,x1,x2)=φ(y1)φ(y2)φ(x1)φ(x2) 则Y1,Y2,X1,Z的联合密度函数为: (方法二)对-∞ 证明:注意到 又 (Z11,Z12,Z21,Z22,…,Zn1,Zn2)′=A(X1,Y1,X2,Y2,…,Xn,Yn)′ 又 而 特别地,当n=2时, 对-∞ 即Z~N(0,1) 一般地,对n≥2,作如下变换: 又Y1,Y2,…,Yn,X1,X2,…,Xn的联合密度函数为: 则Y1,Y2,…,Yn,X1,X2,…,Xn-1,Z的联合密度函数为: fY1,Y2,…,Yn,X1,X2,…,Xn-1,Z(y1,y2,…,yn,x1,x2,…,xn-1,z) 注意到 则 如此进行下去,则有: 于是 由此得:Z~N(0,1) [1] 张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,1997:65-118. [2] 方开泰.实用多元统计分析[M].上海:华东师范大学出版社,1986:67-104. [3] 于秀林,任雪松.多元统计分析[M].北京:中国统计出版社,1999:9-28. [责任编辑:崔海瑛] The Study on Product of Standard Normal Random Variables in the Probability WANG Rong-hua1, XU Xiao-ling2, GU Bei-qing2,LEI PING2 (1. Mathematics and Science College, Shanghai Normal University, Shanghai200234, China;2. Business Information Management School, Shanghai University of International Business and Economics, Shanghai201620, China) standard normal distribution; distribution function; density function; product of random variables 王蓉华(1972-),女,上海人,副教授,主要研究方向应用统计。 上海师范大学骨干教师教学激励计划教研团队建设项目;2015年上海高校外国留学生英语授课示范课程建设(商务统计)项目(A1A-6122-15-002)。 O211.5 A 2095-0063(2016)06-0037-12 2016-06-07 DOI 10.13356/j.cnki.jdnu.2095-0063.2016.06.010




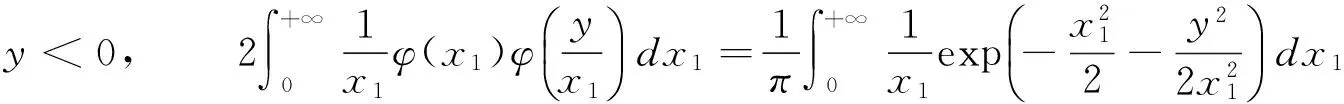
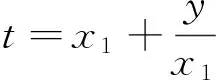


3 容量为2的两个独立标准正态总体样本乘积的分布




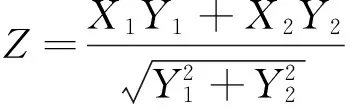

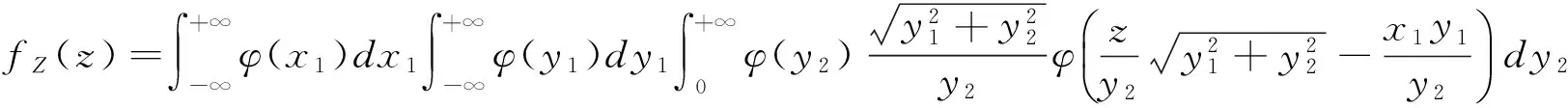
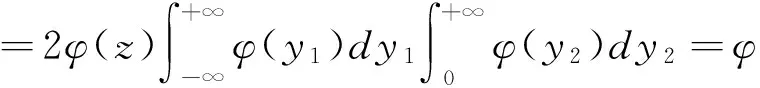
4 容量为n的两个独立标准正态总体样本乘积的分布








