基于空间协方差矩阵的欠定卷积盲源分离

邱珊，李石林

(湖南人文科技学院，湖南 娄底，417000)

基于空间协方差矩阵的欠定卷积盲源分离

邱珊，李石林

(湖南人文科技学院，湖南 娄底，417000)

利用空间协方差矩阵表示的盲源分离模型与瞬时理想模型的一致性，本文提出了基于空间协方差矩阵的欠定卷积盲源分离方法。本方法用零均值高斯随机变量的协方差矩阵来表示各个源信号经过传输信道后的短时傅里叶变换，采用层次聚类估计出高斯随机变量协方差矩阵的初值，并使用极大期望值算法(EM)求解对数似然函数，最后采用维纳滤波法语音增强技术求解时频域内的源信号。通过仿真实验，验证了算法的有效性。

欠定卷积 空间协方差矩阵 维纳滤波

在实际环境中，语音会受到来自噪声或者其他信号的干扰，因此出现了语音增强技术。盲源分离技术是一种有效的增强技术，它在语音信号分离等许多实际人机交互领域有着广泛的应用。盲源分离技术最具代表性的算法是独立分量分析算法，该方法要求观测信号数目大于或者等于源信号的个数也就是非欠定信号。然而，在实际应用中，不可避免地会出现观测信号数目会小于源信号数目的情况,且考虑源信号到各个传感器会产生延时效应的欠定盲源分离问题更加具有研究意义。1991年，Cardoso[1]首次提出欠定情况下的盲源分离问题。关于欠定模型的算法越来越多，当信源具有某种稀疏性时，可以将欠定模型转化成正定模型，从而降低了问题的难度，Karvanen和Cichocki[2]提出了将信号度量成稀疏程度的方法，这时在时域上的稀疏性。而Bofil[3]等人则利用了变换域中的稀疏性。当源信号在时域变换域没有全部充分稀疏时，一些经典的矩阵估计算法就提出来了。Arbret[4,5]等人提出了基于时频比的混合矩阵估计方法。而混合矩阵的列矢量是通过一些聚类算法得到的。如A.Cichocki、P.D.O’Grady等[6]提出的K-均值聚类算法，M.Zibulevsky等[7]提出的FCM聚类算法。而本文采用层次聚类估计出高斯随机变量协方差矩阵的初值，并根据空间协方差矩阵表示的盲源分离模型和瞬时理想模型的一致性，使用极大期望值算法(EM)求解对数似然函数，最后采用维纳滤波法语音增强技术求解时频域内的源信号。

1 欠定盲源分离模型

欠定卷积混合模型可以表示为：

…,I,

(1)

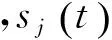
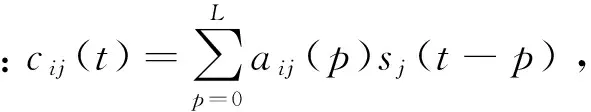
(2)

cij(t)表示第j个源信号的直达波和第j个源信号经L条反射路径形成的回声与直达波一起传入第i个传感器的信号。cj(t)=[c1j(t),c2j(t),…,cIj(t)]T；cj(t)表示第j个源信号的直达波和第j个源信号经L条反射路径形成的回声一起传入I个传感器的信号，表示第j个源信号的在时域内的空间特性。

aj(p)=[a1j(p),a2j(p),…,aIj(p)]T；表示第j个源信号到达所有传感器幅度衰减。

则(1)式可以表示为：

(3)

其中：

(4)

(5)

2 基于空间协方差矩阵的欠定卷积盲源分离算法

Rcj(f,τ)=vj(f,τ)Rj(f),

(6)

其中，Rcj(f,τ)表示cj(t)的协方差矩阵，vj(f,τ)是一个标量，表示第j个源信号在(f,τ)时频点所包含的能量，其初始值为1.Rj(f)表示源信号传输信道的空间特征，是一个时不变的协方差矩阵。因此，观测信号的协方差矩阵可以表示为：

(7)

利用EM算法对Rj(f)，vj(f,τ)进行迭代收敛。

EM算法分为两步： E步：根据参数初始值或上一次迭代的结果计算当前似然函数；M步：将似然函数最大化以获得新的参数值通过循环E步和M步，直到满是某一个收敛条件为止，这就使得被估计的参数能够逼近于真实的参数。EM算法的主要目的是提供一个简单的迭代算法计算后验密度函数,通过EM算法对Rj(f)，vj(f,τ)进行更新：

Estep:

(8)

(9)

(10)

(f,τ))Rcj(f,τ),

(11)

其中，I为单位矩阵。

M step:

(12)

(13)

最大期望算法(EM)估计出v和R之后，通过聚类进行源序(初值)调整

(14)

f∈Fj=1,2,…,J。

(15)

维纳滤波是对平稳信号时域波形的最小均方误差准则下的估计。

假设y(n)表示离散时间的含噪声序列:

y(n)=x(n)+b(n),

(16)

其中，x(n)是所需要的信号，也称为“目标信号”，而b(n)是背景噪声。从y(n)中恢复目标信号x(n)方法是寻找一个线性滤波器h(n)，使得通过滤波器操作后的序列：

(17)

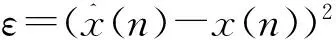
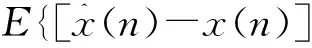
(18)

将式(18)代入(17)，并对式子两边取傅立叶变换，得：

(19)

根据维纳滤波的最小误差准则，本算法用维纳滤波器语音增强技术求解出频域内的源信号[5]

Sj(f,τ)=Gj(f,τ)X(f,τ),

(20)

对频域内的源信号进行反傅里叶变换，估计出时域内的源信号:

(21)

本算法的流程框如图1所示。

图1 算法流程框图Fig.1 Flow chart of algorithm

3 仿真实验分析

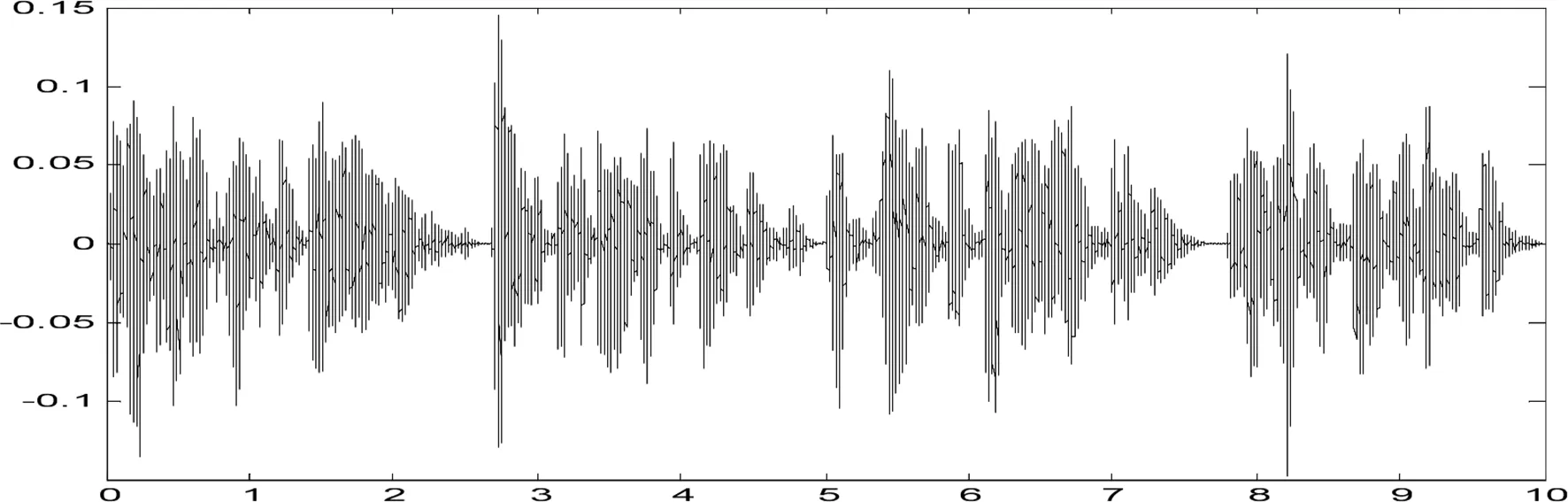
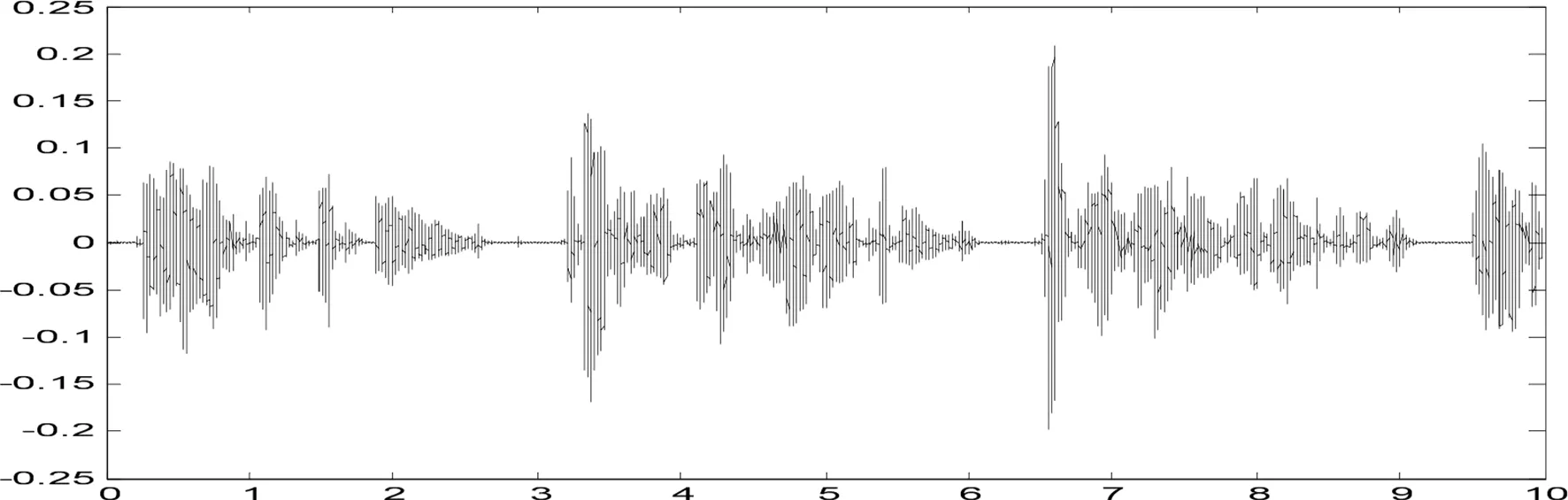
为了验证本算法有效性,本章采用真实房间录音信号进行仿真实验；房间中2个全向传声器接收来3个不同方位的语音信号，3个声源成Y字状等间隔放置。采样频率为16KHz，进行STFT变换时选择窗长为1024的Hanning窗进行FFT，帧移为512。实验采用的混合信号为双声道立体声信号，s1、 s2、 s3分别来自三个不同的人随机说出的语句。图2为三个语音信号的时域图，图3为二个混合信号时域图。

(a)s1时域图

(b)s2时域图

(c)s3时域图

(d)麦克风x1信号时域图

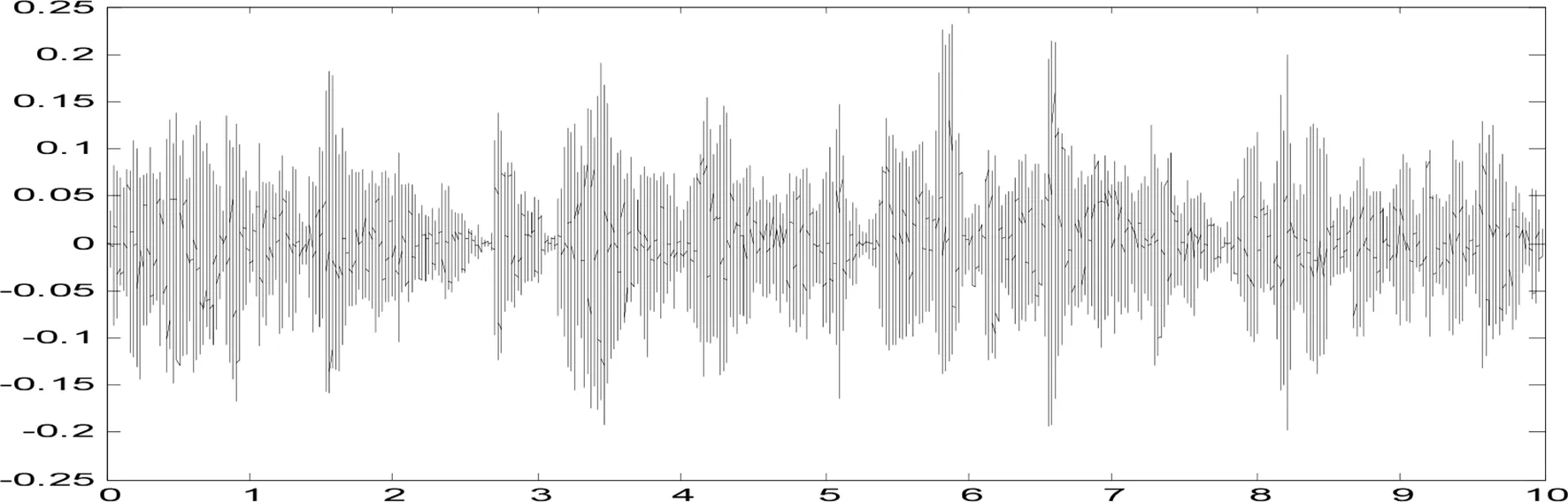
(e)麦克风x2信号时域图

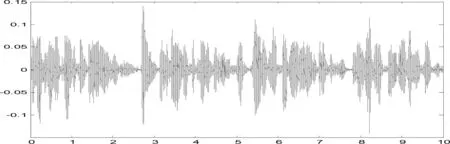
(a)分离出的s1时域图

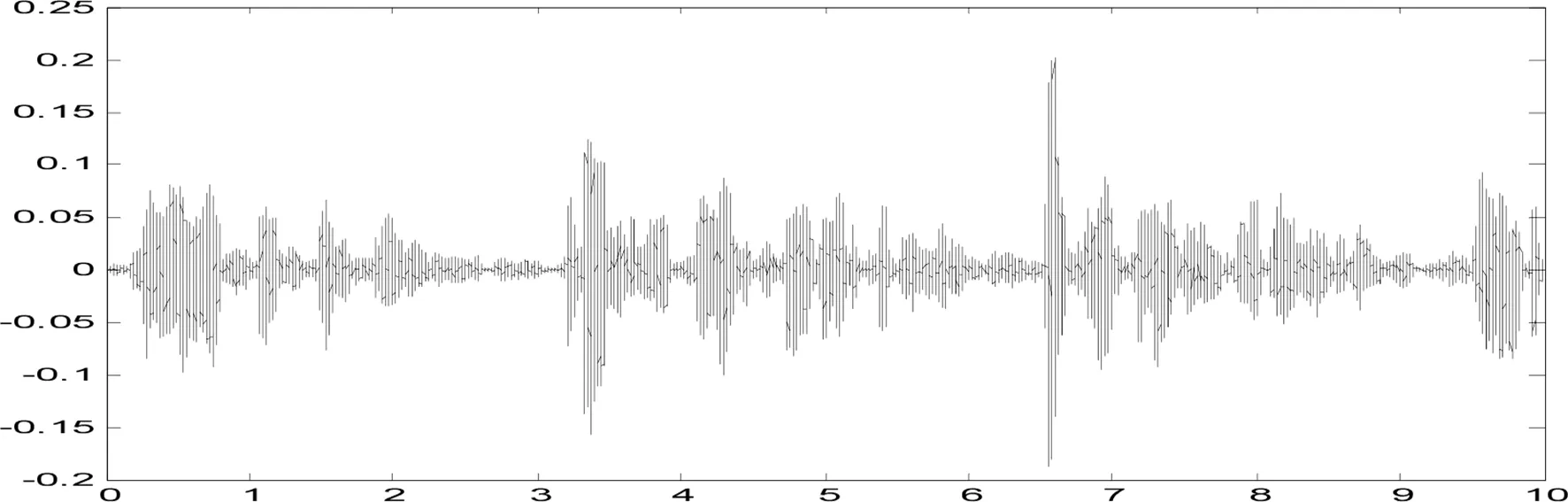
(b)分离出的s2时域图

(c)分离出的s3时域图

将图4本章算法分离出的源信号时域图与图2源信号时域图进行对比，从直观上看三者在波形上都十分相似，从三个图的比较中可以看出上面本章所提出的分离方法的结果十分理想。

为了定性衡量本文算法，采用信号与失真比率SDR(dB)、信号与干扰比率SIR(dB)、信号与人造成份比率SAR(dB)来衡量每个估计出的信号与真实的源信号之间的误差。信号与失真比率、信号与干扰比率、信号与人造成份比率越高，分离出的源信号与真实的源信号就越接近，其误差如表1所示。

表1 三种误差比率

SDR(dB)是用来衡量每个估计信号与源信号之间的误差，信曲比越高，恢复信号与源信号越接近。表2为采用2种算法得到的信曲比的比较结果。

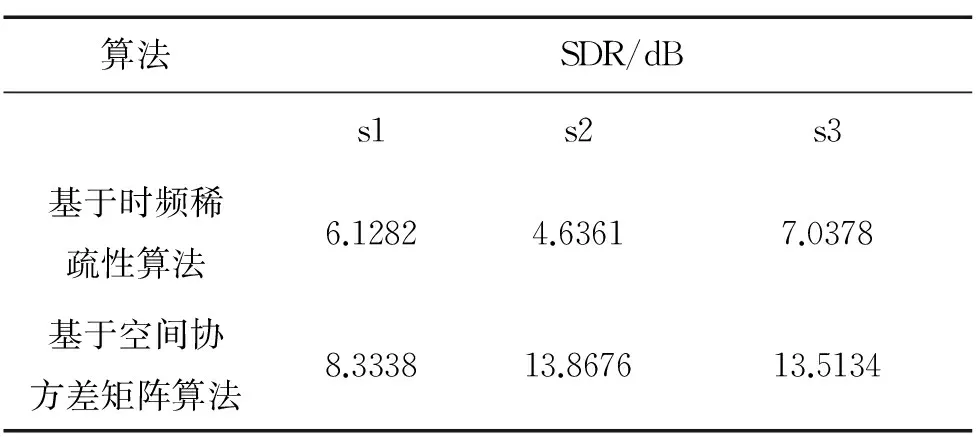
表2 二种方法所得信曲比的比较结果

从表2中我们可以明显看出，使用本文所提出的算法分离出于音频信号的信曲比对比于基于时频稀疏性算法所分离出的音频信号的信曲比得到了极大的提升：采用基于时频稀疏性算法的SDR均值为5.9340dB，采用基于空间协方差矩阵算法的SDR值均值为11.9049 dB。

4 结论

本章主要介绍了基于空间协方差矩阵的欠定卷积盲源分离算法。该算法用零均值高斯随机变量的协方差矩阵来表示各个源信号经过传输信道后的短时傅里叶变换。采用层次聚类估计高斯随机变量协方差矩阵的初值，使用极大期望值算法(EM)求解参数，并利用维纳滤波法语音增强技术求解频域内的源信号。最后采用信曲比(SDR)做为衡量标准与基于时频稀疏性算法进行比较，其结果大大优于基于时频稀疏性算法。

[1]JF Cardoso.Blind identification of more sources than sensors[C]∥In International Conference on Acoustics,Speech,and Signal Processing,1991,5:3109-3112.

[2]Karvanen J,Cichochi A.Measuring sparseness of noisy signals[C]∥4th International Symposium on Independent Component Analysis and Blind Signal Separation,2003:125-130.

[3]Bofill P,Zibulevsky M.Underdetermined blind source separation using sparse representations[J].Signal Processing.2001,81(11):2353-2362.

[4]Arbret S,Vandergheynest P,Carrillo R E,et al.Sparse reverberant audio source separation via reweighted analysis[J].IEEE Transactions on Audio,Speech,and Language Processing,2013,21(7):1391-1402.

[5]Gu F,Zhang H,Wang W,et al.Generalized generating function with tucker decomposition and alternating least squares for underdetermined blind identification[J].EURASIP Journal on Advances in Signal Processing,2013,2013(1):1-9.

[6]Pederson M S.Two-Microphone Separation of speech Mixtures[J].IEEE Transactions on Neural Networks,2008,19(3):475-492.

[7]Ngoc Q.K.Duong.Under-Determined Reverberant Audio Source Separation Using a Full-Rank Spatial Covariance Model[J].IEEE Transactions on Audio,Speech and Language Processing,2010,18(7):1830-1840.

Research on underdetermined convolutive blind source separation based on spatial covariance matrix

QIU Shan，LI Shilin

(Hunan University of Humanities,Science and Technology，Loudi 417009，China)

Based on spatial covariance matrix for utilizing the consistency of the blind source separation model represented by space covariance matrix and instantaneous ideal model,this paper propose a underdetermined convolution blind source separation method.We used the covariance of zero-mean Gaussian random variable to represent the short Fourier transform of each source signal after transmitting in the channel.Adopt the hierarchical clustering to estimate the initial value of the covariance matrix of Gauss random variables.Used the expectation-maximum algorithm to slove the log-likelihood function.At last,using the Weiner filtering speech enhancement technique,figure out the frequency domain source signal.Through the simulation analysis verified the validity of the algorithm.

underdetermined convolutive;spatial covariance matrix;Weiner filtering

1672-7010(2016)04-0045-05

2016-04-15

湖南人文科技学院校级青年基金项目(2015QN02)；湖南省教育厅科学研究项目(15C0726)

邱珊(1986-)，湖南娄底人，助教，硕士研究生，从事自适应信号处理研究；E-mail:272865017@qq.com

TN911.7

A