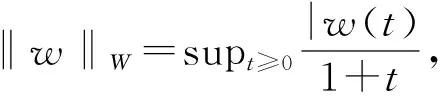分数布朗运动的局部Strassen重对数律
2017-01-03刘永宏李东升李丰兵姜淼
刘永宏,李东升,李丰兵,姜淼
(桂林电子科技大学 数学与计算科学学院,广西 桂林,541004;广西高校数据分析与计算重点实验室,广西 桂林,541004)
分数布朗运动的局部Strassen重对数律
刘永宏,李东升,李丰兵,姜淼
(桂林电子科技大学 数学与计算科学学院,广西 桂林,541004;广西高校数据分析与计算重点实验室,广西 桂林,541004)
应用[1]中方法,研究了分数布朗运动局部Strassen重对数律,将[1]的结果推广到了分数布朗运动情形,也将[2]的结果推广到了局部情形。
分数;布朗运动;平稳增量;局部Strassen重对数律
1 引言与主要结果
布朗运动的Strassen重对数律是一个经典结果,这一结果被人们推广到各种情形,高付清和王清华研究了布朗运动增量的极限定理[3],后来人们又把布朗运动的结果推广到分数布朗运动, Monrad 和 Rootzen研究了分数布朗运动的钟重对数律[6],王文胜[2]得到了分数布朗运动增量的极限定理, 林正炎等研究了分数布朗运动增量在Holder范数下的极限定理[4]。将这些结果推广到局部情形也是人们研究的课题。Gantert研究了布朗运动的局部Strassen重对数律,本文研究分数布朗运动的局部Strassen重对数律,我们的研究结果将Gantert的结果[1]推广到分数布朗运动情形,也将王文胜[2]的结果推广到了局部情形。
设{X(t):t≥0}是一个标准的α阶分数布朗运动具有X(0)=0和平稳增量,且0<α<1,那么{X(t):t≥0}有方差函数
其中{B(s):-∞ 设C[0,1]={f:f为从[0,1]到R的连续函数},赋予上确界范数, 记 下面的定理是本文主要结果: 定理1 对u≥3,定义 (2)对每个f∈K,存在的子列{ξ1/un:n≥1},使得ξ1/un→f(n→∞)。 为证定理,需要下面引理: 引理1 对u≥3, 定义 那么,对P-a.s.,有下面的性质: (1){ηu:u≥3} 在C[0,1]中相对紧,且每个极限点在K中。 (2)对每个f∈K,存在的子列{ηun:n≥1},使得ηun→f(n→∞)。 证明 参看[2]的推论3.1。 下面是定理1的证明 设T:W→W, 定义如下: 注意到T:W→W是等距映射,TH1:H1→H1是等距映射, 而且,P在T下是不变的。 容易计算证明‖Tw‖W=‖w‖W且‖Tf‖H1=‖f‖H1。 我们有 由引理1知{ηu(w)|u≥3}满足引理1中结论(1),(2), 其中 {ηu(w)|u≥3}定义如下: 我们应用T的不变性质,故ξ1/u(w)=Tηu(w)满足定理1中的结论(1),(2), 至此定理1得证。 [1]N.Gantert.An inversion of Strassen’s law of the iterated logarithm for small time[J].The annals of Probability,1993,21(2):1045-1049. [2]W Wang.On a functional limit result for increments of a fractional Brownian motion[J].Acta math.Hungar,2001,93(1-2):153-170. [3]F Gao,Q Wang.The rate of convergence in the functional limit Theorem for increments of a Brownian motion[J].Statistics & probability letters.2005,73:165-177. [4]Z Y Lin,W S Wang,K S Hwang.Functional limit theorems for d-dimensional FBM in Holder norm[J].Acta mathematica sinica,English series.2006,22(6):1767-1780. [5]J Ortega.On the size of the increments of nonstationary Gaussian processes[J].Stochastic Processes and their Applications.1984,18;47-56. [6]D Monrad,H Rootzen.Small values of Gaussian processes and functional laws of the iterated logarithm[J].Probability theory and related fields.1995,101;173-192. Local Strassen’s law of the iterated logarithm for fractional Brownian motion LIU Yonghong,LI Dongsheng,LI Fengbing,JIANG Miao (School of Mathematics and Computing Science,Guilin University of Electronic Technology,Guilin 541004, China;Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guilin University of Electronic Technology,Guilin 541004,China) Using the method in [1],local Strassen’s law of the iterated logarithm for fractional Brownian motion is investigated.The result in [1]is extended to the case of fractional Brownian motion,the result in [2]is also extended to local case. fractional;brownian motion;stationary increments;local Strassen’s law of the iterated logarithm 1672-7010(2016)04-0019-03 2016-09-20 广西教育厅高校科研基金资助项目(YB2014117);国家自然科学基金资助项目(11661025);大学生创新项目资助(201510595198);国家社科基金资助项目(16XTJ002) 刘永宏(1964- ),男,湖北松滋人,教授,博士,从事概率论极限理论研究 O211.4 A
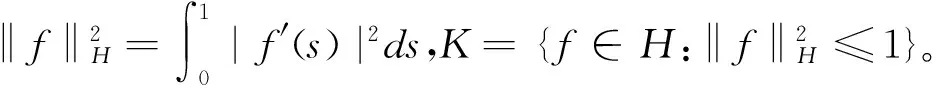
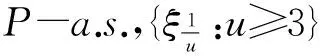
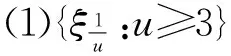
2 定理的证明