一类退化奇点在中心流形上的中心焦点问题

王勤龙

(贺州学院 理学院，广西 贺州,542899)

一类退化奇点在中心流形上的中心焦点问题

王勤龙

(贺州学院 理学院，广西 贺州,542899)

研究了一类三维系统高次奇点在中心流形上的中心问题。通过奇点量的计算得出并证明了这类系统在中心流形上局部可积的充分必要条件。

中心流形；退化奇点；极限环分支

微分自治系统中心焦点的判定主要集中在平面系统[1,2]，而高维系统的中心焦点问题，特别是高维系统中退化奇点的可积性判定等方面的结论还十分少见。这里我们将讨论一类高次奇点在中心流形上的极限环分支问题，具体系统如下

(1)

其中u,d1≠0为实数，z,w,T为复数，且其中akl,bkl满足共轭关系，即

(2)

事实上,系统(1)对应一类实变量微分自治系统(即实共轭系统)，可知系统的原点是一类高次奇点，且有两个零特征根和一个负特征根，因此我们可利用中心流形定理[3]。待定如下近似流形:

u=u(z,w)=u2(z,w)+h.o.t.

(3)

其中u2为z,w的齐二次多项式，h.o.t.表示高次项。然后把(3)代入系统(1)，我们可逐项确定上述(3)式中各项的系数。这里我们得到其前六次项如下:

(4)

其中u2=-d1zw,u4=2δd1z2w2,u3=u4=u5=0,

u6=-id1wz[(a02-b20)d1w3z+(a11d1-b11d1-8iδ2)w2z2+(a20-b02)d1z3w]，

然后把(4)代入系统(1)中的前两个方程可得

本文先计算(5)的奇点量，然后确定系统(1)在中心流形上原点的前几个焦点量，并由此讨论系统在中心流形上奇点邻域可积(即为中心)的条件。

1 系统的奇点量

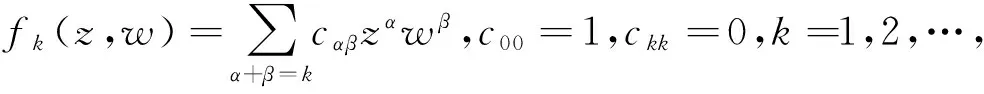
其中μm是系统(5)原点的第m个奇点量，与系统(1)用Poincaré形式级数法求得的原点的第m个焦点量V2m+1有关系V2m+1～iμm,m=1,2,….

在定理1中，记号“～”表示代数等价，定义见[4].

运用定理1和计算机运算化简得：

(6)

在上述的表达式中已置μ1=μ2=...=μk-1=0,k=2,3。

进一步地，由式(2)我们有

定理3 在系统(1)中心流形上，原点的前3个焦点量V2i+1(2π),i=1,2,3如下:

V3=2πd1B1,

V7=2πd1[(A0-A2)2+(B0+B2)2]。

(7)

2 极限环分支

现在我们可以讨论系统(1)原点在中心流形上的中心焦点问题，这里所用概念及方法详细可见文献[5-7]

定理4 在系统(1)中心流形上原点前3个焦点量全部为零的充分必要条件是:

B1=0，A0=A2，B0=-B2，

(8)

也即

b11=a11，a20=b02，b20=a02

(9)

定理5 在中心流形上，系统(1)在其原点邻域内可积(原点为中心)的充分必要条件是(8)或(9)成立。

证:根据定理4必要性明显成立，只需证充分性，当上述条件(8)或(9)成立时，系统(1)为:

(10)

很容易验证系统(10)前两个方程的首次积分为:zw=c0,由此进一步可求得u=c1eiT+c0d1或者u=c1e-t+c0d1，其中c0,c1为积分常数，可见系统(1)中心流形上在原点邻域内可积，也即原点为中心。

[1]叶彦谦.多项式微分系统定性理论[M].上海：上海科学技术出版社，1995.

[2]刘一戎，李继彬.平面向量场的若干经典问题[M].北京：科学出版社，2010.

[3]Carr J. Applications of Centre Manifold Theory[M].Appl Math Sci vol 35,New York:Springer,1981.

[4]刘一戎.一类高次奇点与无穷远点的中心焦点理论[J]，中国科学，A,2001，(1)：37-48.

[5]Wang Q,Liu Y,Chen H.Hopf bifurcation for a class of three-dimensional nonlinear dynamic systems,Bulletin des Sciences Mathematiques[J].2010，(134)：786-798.

[6]Wang Q,Huang W,Feng F.Multiple limit cycles and centers on center manifolds for Lorenz system[J].Applied Mathematics and Computation 2014,(238):281-288.

[7]袁月定.一类具有常数存放率的Kolmogorov捕食系统的极限环[J].邵阳学院学报(自然科学版)，2014，11(1)：1-4

Center-focus problem of degenerate singularity on center manifold

WANG Qinlong

(School of Science,Hezhou University,Hezhou 542899,China)

In this paper,center-focus problem of the degenerate equilibrium of a three-dimensional system is investigated.By computing the singular point quantities,the center conditions of the origin on center manifold is given.

center manifold;degenerate singularity;limit cycle bifurcation

1672-7010(2016)04-0016-03

2016-09-20

国家自然科学基金资助项目(11461021)；广西自然科学基金资助项目(2015GXNSFAA139011)；广西高校符号计算与工程数据处理重点实验室项目资助

王勤龙(1972-)，男，湖北荆州人，教授，博士，从事微分方程定性理论、计算机符号计算研究

O175.1

A