基于多目标混合遗传算法认知无线电频谱分配

刘蕊蕊

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

基于多目标混合遗传算法认知无线电频谱分配

刘蕊蕊

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

在认知无线电的频谱分配问题中，论文提出基于图着色模型的多目标混合遗传算法。该算法采用多目标函数为适应度函数，将模拟退火算法嵌入到遗传算法的循环中，弥补遗传算法局部搜索能力的不足。仿真结果表明多目标混合遗传算法能增强全局搜索能力，提高收敛速度，更好地实现系统效益最大化。

认知无线电；频谱分配；多目标混合遗传算法；模拟退火算法

随着远程通信产业的迅速发展，无线电频谱的需求急速上升。再加上现有频谱资源利用率不到10%， 导致频谱资源越来越稀缺。[1]为解决这一问题，认知无线电(CR)的概念[2]被Joseph Mitola 博士首先提出。(CR)是一种能感知周围环境的智能无线电系统，并可以使用智能的学习方法，与周围环境进行信息交流。因此，本地频谱可以被认知用户自适应占用，同时在通信过程中不会给主用户带来不利干扰，实现频谱共享，[3]大大提高频谱利用率。

认知无线电频谱分配现已成为研究热点。文献[4]应用量子遗传算法解决频谱分配问题。文献[5]将遗传算法(Genetic Algorithm， GA)应用到谱分配领域，验证了(GA)在此领域的有效性。文献[6]认为遗传算法虽然在网络效益上高于经典算法，但容易陷入局部最优解。文献[7]提出基于遗传算法的MOP 算法(Max-Overall-Performance Algorithm， MOPA)，通过改变适应度函数来提高系统效益。文献[8]和文献[9]提出以进化博弈论模型为基础的频谱分配。其它频谱分配问题的数学模型有图着色模型，[10-11]拍卖竞价模型等。[12-13]

本文针对静态系统给出解决方案。首先，建立基于图着色模型的认知无线电频谱分配方法，然后采用多目标遗传算法优化给出问题的求解方法。为保证遗传算法的全局搜索性， 并避免遗传算法陷入局部最优解，我们在遗传算法过程中引入模拟退火算法。

本文结构如下: 首先定义认知无线电频谱分配模型相关的模型矩阵；然后给出多目标混合遗传算法的适应度函数，遗传算子。借助MATLAB 仿真工具，文章最后给出了静态系统的仿真结果，并与其它方法进行比较，说明了本文算法的有效性。

1 认知无线电频谱分配模型

论文采用信道可用性矩阵，信道奖励矩阵，干扰限制矩阵，免冲突信道分配矩阵来描述图着色模型。假设系统内有n个认知用户，m条信道。各个矩阵定义如下:

定义1 信道可用性矩阵

L={lij|lijε∈{0,1}}n×m

表示认知用户i(1≤i≤n)是否可以使用信道j(1≤j≤m)。若可以使用，则lij=1；否则lij=0。

定义2 信道奖励矩阵

B={bij|bij>{0,1}}n×m

其中bij代表i(1≤i≤n)使用信道j(1≤j≤m)所获得的奖励。

定义3 干扰限制矩阵

C={cikj|cikj∈{0,1}}n×n×m

表示网络中的干扰。当i=k时，ciij表示授权用户与认知用户之间的干扰，若认知用户i使用频谱j时对同时使用该频谱的授权用户产生干扰，则ciij=1，反之ciij=0；当i≠k时，表示认知用户之间的干扰，若认知用户i与k同时使用频谱j，就会产生干扰，则cikj=1，反之cikj=0。

定义4 免冲突信道分配矩阵

A={aij|aij∈{0,1},aij}≤lij}n×m

当aij=1时表示频谱j分配给了认知用户i，反之aij=0。同时，分配矩阵A必须满足干扰矩阵C的约束：

cikj=1,∀1≤j≤m; 1≤i, k≤n, i≠k⟹aij·akj=0

2 多目标混合遗传算法设计

2.1 染色体编码。

论文采用二进制编码方法对染色体进行编码。当可用性矩阵L中的元素等0时，分配矩阵A所对应的元素必为0。为了减少运算，提高运行效率，仅对lij=1的位置编码，故矩阵L中元素为1的个数决定染色体编码之后二进制串的长度。染色体的编解码示例如图1所示: 假设有四个用户，五条信道，Xi代表第i条染色体，xij∈[0,1], j=(1,2,3,4,5,6,7)。

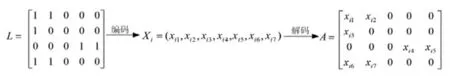
图1 染色体编解码示例

原始群体中每个染色体的二进制编码都是随机形成的并且容易受到交叉和突变的影响， 因此它并不完全满足预先定义的干扰矩阵C，故提出以下方法进行改进:

对于所有的频谱j(1≤j≤m)，观察所有的数对(i,k)是否满足cikj=1；若cikj=1，检查aij与akj是否同时为1，如果同时为1，则随机选取一个为0。

2.2 适应度函数。

在论文中， 我们考虑以下目标函数:

系统总效益函数

最大比例公平函数

其中Ai(i=1,2,3,…,n)为A的第I行元素。

本文采用多目标函数的权重方法获得遗传算法的总适应度函数。可以随机调整系统效益和最大比例公平的权重值，若认知用户间的频谱分配着重于最大比例公平，则将最大比例公平函数U的权重设的大些，反之亦然。设R的权重为α，U(A)fair的权重为β(α+β=1)，则总目标函数为

f(A)=α·R(A)+β·U(A)fair

2.3 选择，交叉，变异操作。

本文采用“轮盘赌”选择法。在该方法中，每个个体的选择概率与它的适应度值成比例。设群体大小为n，其中个体Xk的适应度为fk(A)，则Xk被选择的概率

选择个体后，随机组成交配对，为后面的交叉操作创造条件。

交叉操作采用两点交叉，即在个体中随机设定两个交叉点，然后将两交叉点之间个体结构互换。自适应交叉概率

自适应变异概率

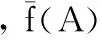
2.4 模拟退火操作。

模拟退火算法 (Simulated Annealing，SA) 以通过选择，交叉，变异等操作产生的种群为当前解，在邻域内进行局部搜索，产生优化的新种群。并进入到下一个遗传算法的进化循环中。为了更好地实现本文算法对频谱的分配，SA直接操作GA生成种群的染色体，设GA 的进化代数g为SA的退火时间，GA 的适应度函数看作SA的能量函数。

模拟退火操作具体过程如下:

(1) 新染色体产生方式。

当前解Xk解码为免冲突信道分配矩阵A，随机生成一个扰动量W(长度和认知用户的个数相等)，随机替换A的某个信道对其进行约束操作，形成新的分配矩阵A，将A映射为新生的染色体Xj。

(2) 温度更新函数。

为了计算简便，采用时齐的方式进行温度管理，即：

T(g)=K·T(g-1)

K为Boltzmann常数，其中T(g)为当前退火温度。

(3) 新染色体接受准则。

因本文所求的是极大值，故新解的接受率如以下函数所示：

fk(A)，fj(A)分别为染色体Xk与Xj的适应度。

3 多目标混合遗传算法流程

设最大遗传代数G=500为终止条件，多目标混合遗传算法流程如下：

(2)种群初始化。随机选取n个初始个体组成原始群体Q(g)，令进化代数g=0并对染色体进行二进制编码，得到二进制串X,X2,X3,…XN。

(3)将染色体Xi(i=1,2,3,…,Xn)的第s个字节映射到aij，其中(i,j)是L1中的第s个元素，并且1≤s≤d。对于任意的j，观察所有的数对(i,k)是否满足cikj=1；若cikj=1，核查一下aij与akj是否同时等于1。若同时为1，则随机选取一个为0，令一个保持不变。

(4)根据权重值计算适应度函数值。

(5)对Q(g)执行选择、交叉、变异操作。得到新种群Q1(g)。

(6)对种群Q2(g)中所有染色体进行模拟退火操作。得到新的群体Q3(g)。

(7)终止条件判断。若g≤G(最大遗传代数)，则g=g+1，将Q3(g)作为新的下一代群体，然后转到混合算法的第二步；若g>G，则输出结果，算法结束。

4 仿真结果与分析

本文仿真是在Windows环境中利用MATLAB建立的。对本文算法和基于图着色模型的多目标遗传算法和一般遗传算法进行比较。在仿真过程中参数设置如下:目标函数权重值α=0.6，β=0.4，认知用户n=10，信道m=18。随机生成L，B，C矩阵，L，C中的元素由0，1组成，B中元素为[0,n]中的自然数。

随着迭代次数的增加，系统效益逐渐增加，本文算法迭代250次达到最优解，其他两种算法迭代400次左右达到最优解，很明显本文算法收敛速度较快，且系统效益更高，如图2所示。

随着认知用户的增加，系统效益逐渐减少，但在认知用户相同情况下，本文算法的系统效益明显优于其他两种算法，如图3所示。

图4表示系统效益随试验次数的变化曲线图，本文算法的优越性虽然在很少情况下效果不明显，但在大部分情况下系统效益明显优于其他两种算法。

图5表示三种算法时间开销随迭代次数的变化曲线图，由图5可知:算法的时间开销随着迭代次数的增加逐渐上升，本文提出的算法分配时间开销明显比多目标遗传算法和一般遗传算法的要少，故此算法提高了系统的运行效率。

结束语

论文针对现有频谱分配算法的不足，将多目标混合遗传算法应用到频谱分配中，提高了频谱的利用率以及系统效益，同时还减少了系统的运行时间，提高了收敛速度。通过仿真可以得出以下结论:该算法系统效益高，收敛速度快，优化过程较简单.故此方法为提高频谱利用率，解决频谱分配问题提供了新思路。

[1]Akella A，Judd G，Seshan S，Steenkiste P. Self-management in Chaotic Wireless Deployments[J]. International Conference on Mobile Computing and Networking，2005，13(6):737-755.

[2]Milola J. Making Cognitive Radio:Software Radios More Personal[J]. IEEE Personal Communications，1999，6(4):13-18.

[3]Akyildiz IF，Lee W，Vuran MC，Mohanty S.Next Generation Dynamic Spectrum Access Cognitive Radio Wireless Networks: A Survey[J].Computer Networks，2006，50(13):2127-2159.

[4] Zhao Zhijin，Peng Zhen，Zheng Shilian，et al. Cognitive Radio Spectrum Assignment Based on Quantum Genetic Algorithm[J]. Acta Physica Sinica，2009，58(2):1358-1363.

[5] Mustafa Y，Nainay E.Island Genetic Algorithm-based Cognitive Networks[D].Blacksburg，USA: Virginia Polytechnic Institute and State University，2009.

[6]Zhao Zhijin，Peng Zhen.Cognitive Radio Spectrum Allocation Using Evolutionary Algorithms[J]. IEEE Transactions on Wireless Communications，2009，8(9):4421-4425.

[7]Wen Kai，Fu Lingsheng，Li Xuesong.Genetic Algorithm Based Spectrum Allocation for Cognitive Radio Networks[J]. Advances in Computer，Communication，Control & Automation，2012，693-700.

[8]Nie N，Comaniciu C. Adaptive Channel Allocation Spectrum Etiquette for Cognitive Radio Networks[J]. IEEE Computer Society，2005，11(6):269-278.

[9]Ni Qiufen，Zhu Rongbo，Wu Zhenguo，Sun Yongli.Game-based Spectrum Allocation Algorithm in Cognitive Radio Networks[J]. Springer Berlin Heidelberg，2013，1-13.

[10]Tandra R，Mishra SM，Sahai A. What Is a Spectrum Hole and What Does It Take to Recognize One[J]. Proceedings of the IEEE，2009，97(5):824-848.

[11]Chunyi Peng，Haitao Zheng. Utilization and Fairness in Spectrum Assignment for Opportunistic Spectrum Access[J]. Mobile Networks and Applications，2006，11(4):555-576.

[12]Huang J，Berry RA，Honig ML. Auction-based Spectrum Sharing[J].Mobile Networks and Applications，2006，11(3):405-408.

[13]Kloeck C，Jaekel H，Jondral FK. Dynamic and Local Combined Pricing，Allocation and Billing System with Cognitive Radios[J]. IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks 2005，73-81.

Class No.:TN92:O29 Document Mark：A

(责任编辑：宋瑞斌)

Allocation of Cognitive Radio Spectrum Based on Multi-objective Hybrid Genetic Algorithm

Liu Ruirui

(School of Mathematics and System Science, Shandong University of Science and Technology, Qingdao，Shandong 266590，China)

As for the cognitive radio spectrum allocation，this paper puts forward a multi-objective hybrid genetic algorithm based on graph coloring model. The algorithm adopts the multi-objective function as the fitness function, embedding the simulated annealing algorithm into the cycle of basic genetic algorithm in order to make up the lack of local search ability of genetic algorithm. Simulation results show that multi-objective hybrid genetic algorithm can enhance the global search ability and convergence speed，and can realize the system benefit maximization better.

cognitive radio; spectrum allocation; multi-objective hybrid genetic algorithm; simulated annealing algorithm

刘蕊蕊，在读硕士，山东科技大学。研究方向：计算理论与数据处理。

1672-6758(2016)12-0059-4

TN92:O29

A