基于自平衡静载试验的单桩承载性能分析
2016-12-30刘江磊
刘江磊
(铁道第三勘察设计院集团有限公司,天津 300251)
基于自平衡静载试验的单桩承载性能分析
刘江磊
(铁道第三勘察设计院集团有限公司,天津 300251)
建立自平衡试桩与传统静载荷试验的分析模型,采用有限元法模拟桩土受力体系。根据实测轴向力分布曲线和荷载-位移曲线反演拟合出双曲线力学模型参数。将反演得到的模型参数应用于同等条件下桩顶加载试桩的分析模型中,确定出等效荷载-位移曲线,并与简化转换法和精确转换法确定的荷载-位移曲线进行可靠性和适用性评价。结果表明,根据有限元法得到的荷载-位移曲线与按相关规范、简化法、精确法确定的极限承载力都很接近,三种数据转换方法均合理。
自平衡试桩法 有限元模拟 极限承载力 荷载沉降曲线
自平衡静载荷试验[1-3]是由基桩自身反力平衡来测定单桩承载力的一种测试方法。通过预埋在桩身截面处的荷载箱加压,上、下两段桩体会受到一对大小相等,方向相反的作用力,且分别同时产生上、下位移,调动桩侧摩阻力与下段桩底端阻力发挥,从而实现试桩的自身反力平衡,试验原理如图1所示。
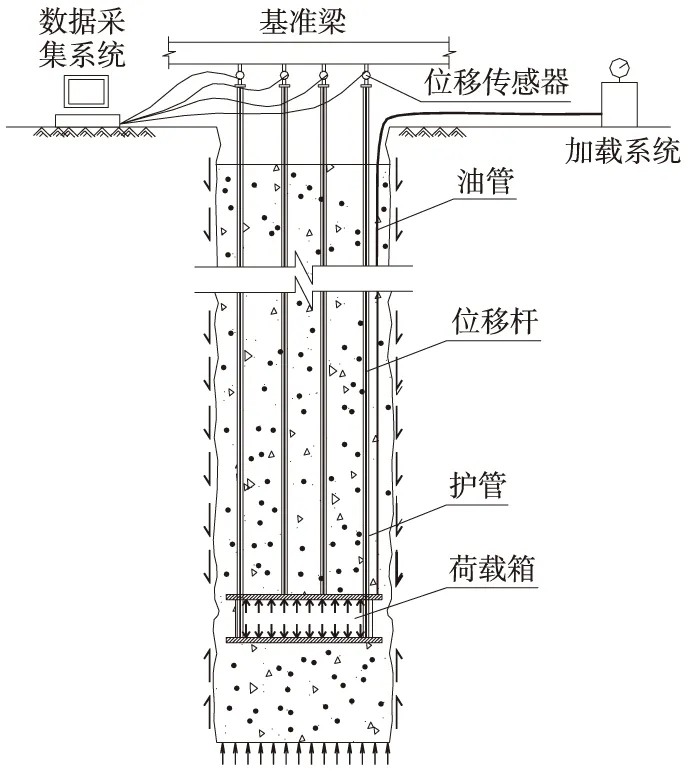
图1 桩承载力自平衡试验示意
根据试验数据绘制“力-位移”关系图,从而确定单桩承载力。与传统的测试方法相比,该方法不需要压重平台或反力支架,不受场地环境的限制,且不需准备压重物,整个过程省时省力。
1 工程概况
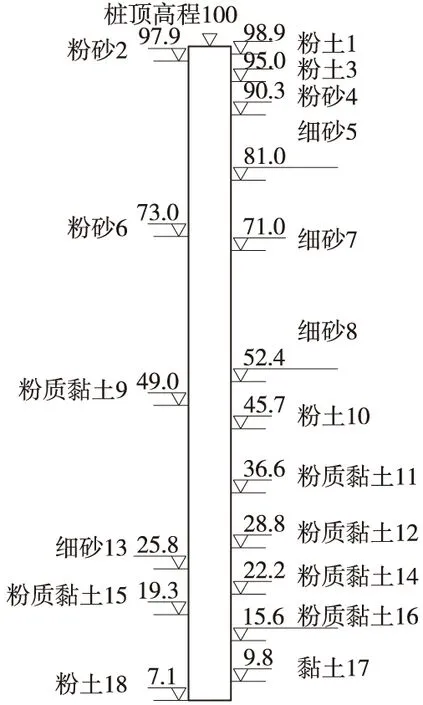
图2 桩土剖面(单位:m)
某铁路跨黄河特大桥项目的自平衡试桩TSZ1场地桩土布置如图2所示,沿桩深共穿过18个土层。设计桩长90 m,桩径1.8 m,实际桩长91.987 m,实际平均桩径1.825 m。荷载箱埋深于高程为25~25.5 m位置。荷载共分8级加载,各级加载量分别为3 814 kN、5 721 kN、7 628 kN、9 536 kN、11 443 kN、13 350 kN、15 258 kN、17 164 kN。测得荷载-位移曲线见图3,加载到各级荷载桩身轴力分布曲线见图4。
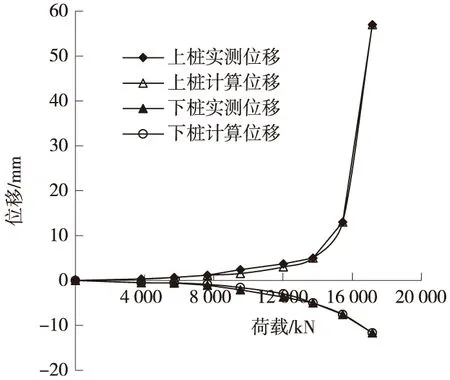
图3 TSZ1自平衡静载荷试验Q-s拟合曲线
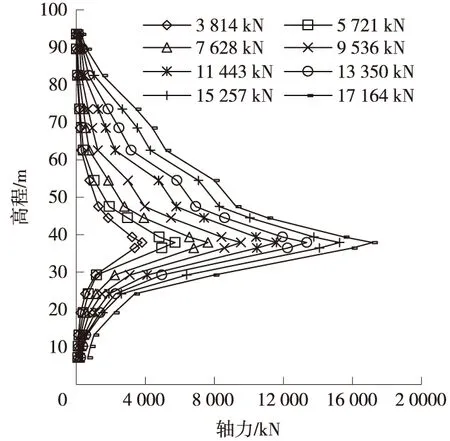
图4 TSZ1试桩轴力
2 有限元分析模型建立
2.1 基本假设
桩土体系分析模型见图5和图6。
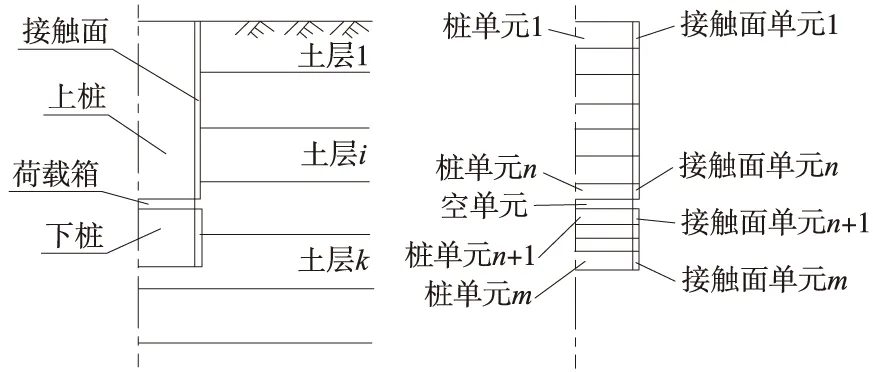
图5 自平衡测试法模型及单元划分
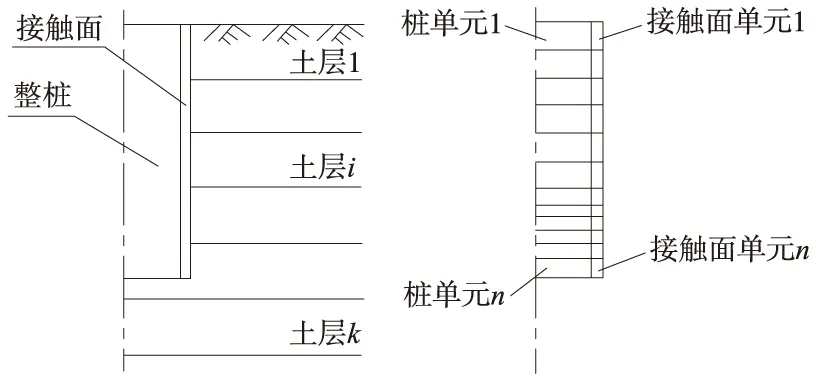
图6 传统静载试验模型及单元划分
(1)采用平面轴对称模型模拟桩体和桩周土体;
(2)荷载箱位置为空单元,上下段桩所受载荷相同,分别作用于上段桩桩底和下段桩桩顶;
(3)桩身混凝土单元为连续均质弹性体,材料类型设为线弹性材料;
(4)土体假设为均质地基,材料类型为非线性弹性模型,本构模型选用邓肯-张模型;
(5)考虑土体与桩体的接触,分析过程中桩体与土体之间摩擦系数不变。
2.2 本构模型
(1)桩身本构模型
桩身为线弹性体,采用C30混凝土,弹性模量选为3.0×104MPa。
(2)土体本构模型
桩周土体通常采用弹塑性模型或线弹性模型,模型选用邓肯-张模型[4,5],邓肯-张双曲线模型的本质在于假定土应力应变之间的关系具有双曲线性质。
(3)接触面力学模型
桩土接触面采用无厚度的Goodman单元,并采用双曲线形剪应力-切向位移差的力学模型,设桩土接触面间的剪应力为τ,接触面两侧的切向位移差为Δu,则两者之间满足如下关系[6]
其中a=1/Kτ,max,b=1/τult,式中,Kτ,max为初始切线刚度,τult为最终剪应力,如图7所示。
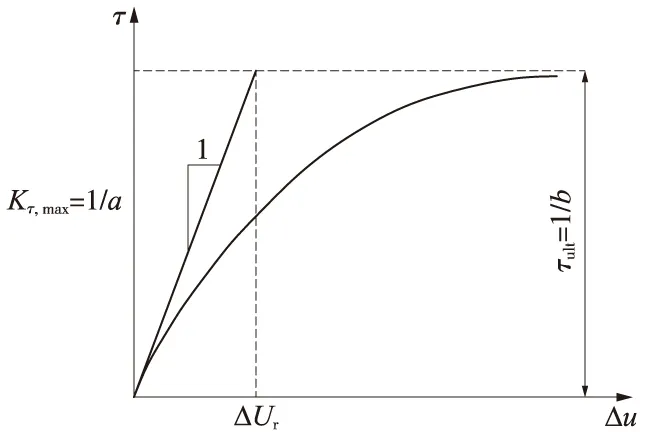
图7 τ~Δu关系曲线
式中,ΔUr—参考位移。
在此应指出,常规计算方法中桩的极限侧摩阻力τf与上述公式中最终剪应力τult的关系为
式中,Rf为破坏比,一般取值范围为0.8~0.9。
3 分析步骤和结果
首先建立自平衡试桩桩土分析计算模型,拟合自平衡试桩实测得到的桩身轴力和荷载位移曲线,确定出桩周土力学模型及桩阻力参数。将这些参数应用于桩顶加载计算模型,确定出桩顶加载的荷载位移曲线,对精确转换法、有限元法及简化转换法三种方法确定的极限承载力进行比较。
3.1 桩-土接触面模型参数确定
由于桩身两个断面之间轴向力差值等于这两个断面间的桩侧阻力,则桩侧阻力沿深度的分布可以根据桩轴力沿深度的变化确定。通过桩身轴力曲线的拟合,可以确定桩土接触面模型参数,也保证了桩端阻力和桩侧阻力分布与实际情况吻合。
采用5 721 kN、11 443 kN、17 164 kN三个等级荷载数值模拟轴向力分布曲线,得到自平衡桩的轴向力分布曲线(如图8所示)。其中相对应的桩-土接触面的力学模型参数见表1。
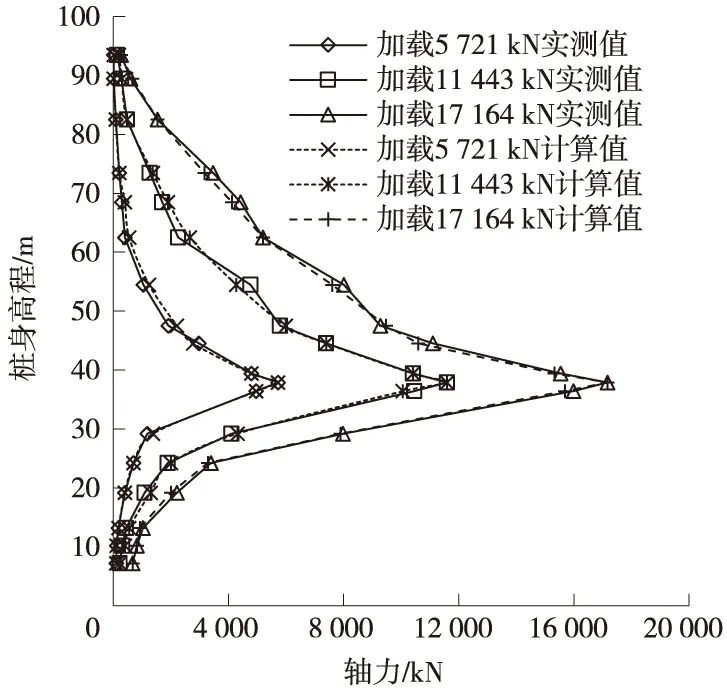
图8 TSZ1试桩轴向力分布曲线
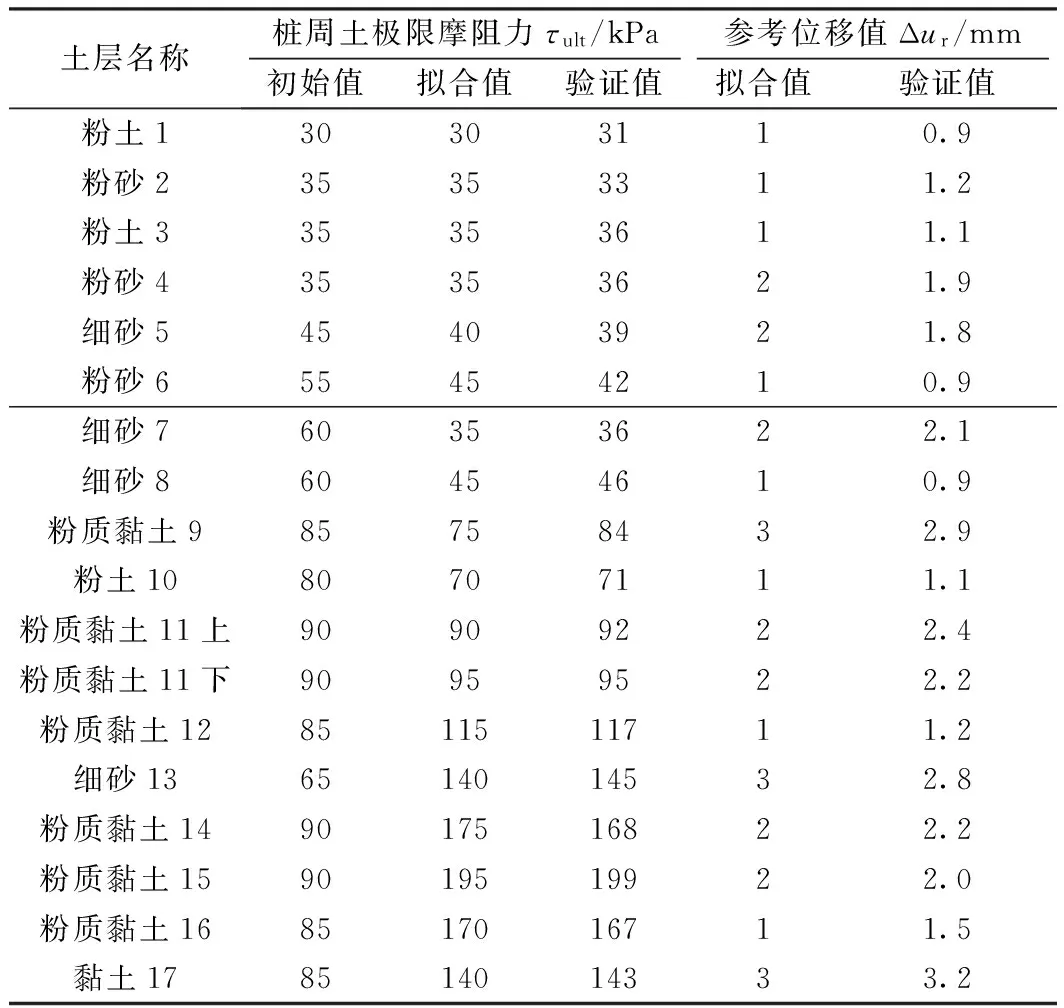
表1 TSZ1试桩接触面的力学模型参数
3.2 桩侧土模型参数确定
可以根据荷载-沉降曲线拟合调整参数,最终确定参数。采用初始参数模拟得到的桩顶-沉降曲线一般与实际测试结果不同,再对参数进行调整,通过数值模拟,最后得到的荷载位移曲线与实际测试结果如图3,计算曲线能够与实测曲线很好地拟合。反演得到的桩周土体邓肯-张模型参数见表2。
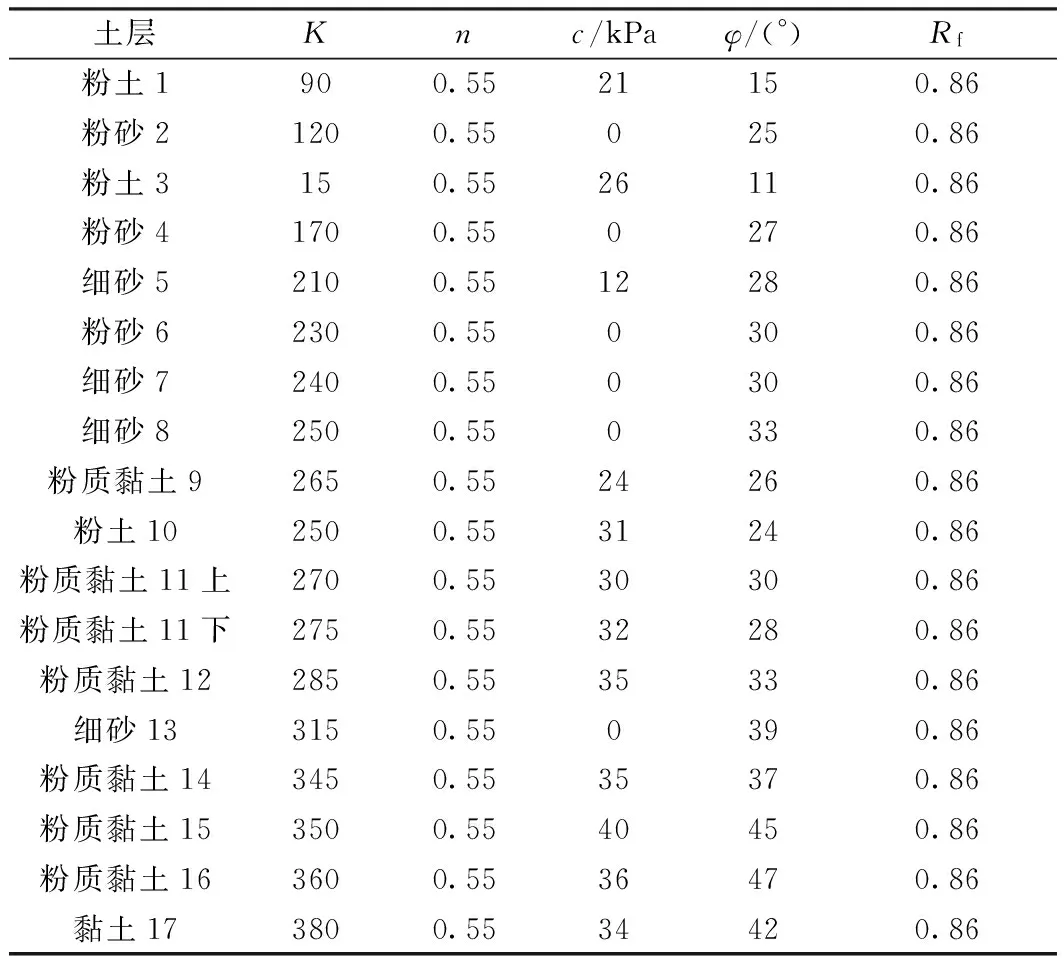
表2 TSZ1试桩桩周土邓肯-张本构模型参数
3.3 等效荷载-沉降曲线的确定及对比
通过以上自平衡试桩的模拟分析,得到桩周土体及桩-土接触面的本构模型参数,相同土层条件下,加载方式改为桩顶加载,即可得到整桩等效桩顶加载荷载-位移曲线。由于上段桩受力状态的改变,上段桩所受负摩阻力转变为正摩阻力及松土效应消失,在桩顶加载的数值模拟时,上段桩的接触面极限侧摩阻力取表1的极限侧摩阻力除以一个系数λ,其他土体参数和接触面参数与自平衡试桩加载方式时相同。其中λ按如下方法取值:粉土0.8,粉砂0.7,细砂0.7,粉质黏土0.8。下段桩接触面的极限侧阻力值直接采用表1中相应的极限侧阻力拟合值,不考虑加载方式变化的影响。由整桩模拟分析得到的整桩荷载沉降曲线如图9所示。图9中也同时给出了按精确转换法和简化转换法[7,8]确定的整桩荷载位移曲线。比较三种方法确定的整桩荷载位移曲线可发现:
(1)采用有限元分析得到的等效荷载-位移曲线提供了一条经过弹性线性段到弯曲过渡段,最后沉降急剧增加至破坏的完整等效桩顶加载的荷载-位移曲线,曲线完整,能够适应各种相关规范标准。
(2)由简化转换法和精确转换法确定的等效桩顶加载的荷载-位移曲线很接近,同时,该两种方法得到的荷载位移曲线与自平衡模拟得到的荷载位移曲线也基本重合。由此可得,这三种方法用于自平衡试桩结果向桩顶加载结果的转换具有一定的可靠性。
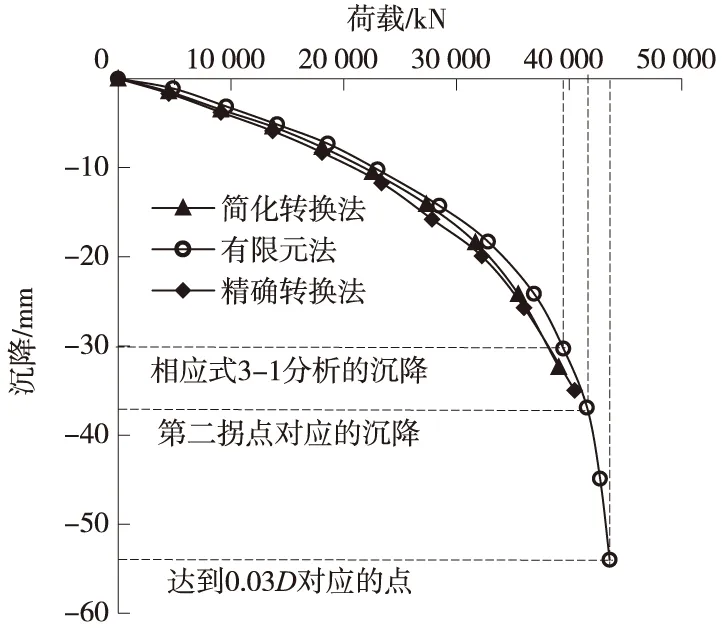
图9 TSZ1试桩等效荷载-位移曲线比较
3.4 极限承载力的确定
《基桩静载试验自平衡法》(JT/T738—2009)规定
式中Qu——单桩竖向抗压极限承载力;
Qu下——自平衡试桩上段桩极限承载力实测值;
Qu下——自平衡试桩下段桩极限承载力实测值;
W——自平衡试桩的荷载箱以上桩,即上段桩的自重,若荷载箱处于透水层,取浮自重;
γ——试桩的抗托系数,根据荷载箱上部土的类型确定。若上部有不同类型的土层,取加权平均值。
根据由有限元模拟得到的荷载-沉降曲线,采用如下两种标准确定试桩的整桩极限承载力[9,10]:
(1)沉降等于0.03倍桩直径时对应的荷载值;
(2)荷载-沉降曲线中第二个拐点对应的荷载值。
图9在有限元法得到的荷载-位移曲线上标出了按上述两种标准确定的点所对应的极限荷载值及位移值。为了比较各种方法确定的极限荷载,在图9中有限元法得到的荷载-位移曲线上也标出了按公式(5)计算的极限荷载及对应的位移值。表3给出了上述三种方法及简化转换法和精确转换法所确定的沉降量与极限承载力。
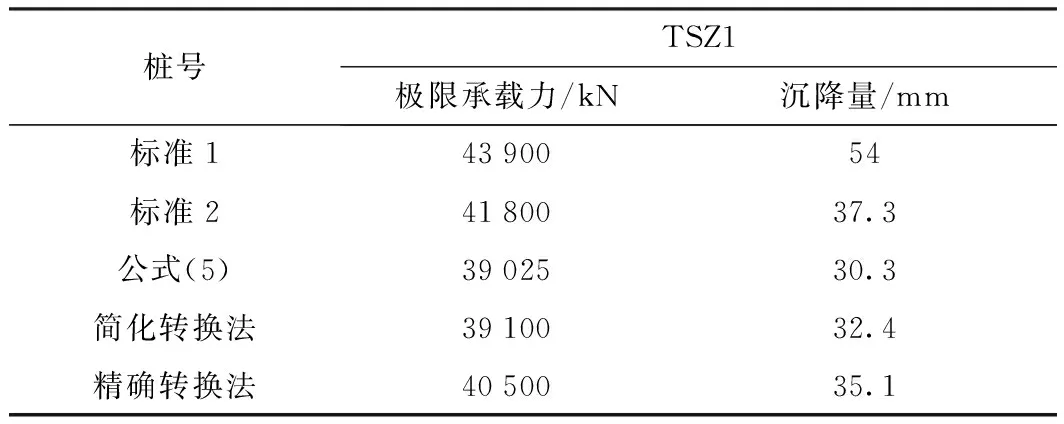
表3 TSZ1试桩按不同方法确定的极限承载力及沉降量
4 结论
(1)以武西高速公路桃花峪黄河大桥某桩基检测试验为背景,采用自平衡现场试验对桩基承载性能进行研究,并通过有限元数值模拟反分析的方法,拟合确定桩周土和接触面力学参数,分析钻孔灌注桩整桩性能,为试桩结果提供依据。
(2)所采用的反分析拟合参数方法能很好地模拟桩与桩周土体的相互作用,模型参数可以和传统桩分析方法的模型参数相对应,如土体的极限侧阻和接触面刚度等都便于引用到传统载荷桩分析中。通过数值模拟结果与实测结果的对比,更加验证了自平衡试桩的可靠实用性及转换方法的准确性。
(3)简化转换法和精确转换法确定的等效桩顶加载的荷载-位移曲线很接近。同时,该两种方法得到的荷载位移曲线与自平衡模拟得到的荷载位移曲线也基本重合。由此可得,这三种方法用于自平衡试桩结果向桩顶加载结果的转换具有一定的可靠性。
(4)有限元分析得到的等效荷载-位移曲线提供了一条经过弹性线性段到弯曲过渡段,最后沉降急剧增加至破坏的完整等效桩顶加载的荷载-位移曲线,曲线完整,能够适应各种相关规范标准。
[1] 史佩栋.桩基工程技术[M].北京:中国建材工业出版社,1996:400-409[2] 龚维明,戴国亮.桩承载力自平衡测试技术及工程应用[M].北京:中国建筑工业出版社,2005:1-45
[3] 史佩栋.桩基工程手册[M].北京:中国建筑工业出版社,1995:1-68
[4] 庄茁,张帆,岑松,等.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005:7-16,188-205,312-384
[5] 李桅.基于ANSYS10.0桩土共同作用分析[J].科技咨询导报,2007(16):1-3
[6] 王博林.自平衡法桩土荷载传递机理及承载特性研究[D].兰州:兰州交通大学,2012:21-35
[7] 马远刚.基桩承载能力自平衡测试技术及其工程应用[D].武汉:中国科学院武汉岩土力学研究所,2010:56-78
[8] 龚维明,戴国亮,蒋永生,等.桩承载力自平衡测试理论与实践[J].建筑结构学报,2002,23(1):82-88
[9] 李正祥.铁路桥梁工程单桩承载力测试的自平衡法[J].铁道标准设计,2010(6):63-66
[10]戴国亮,龚维明,刘欣良.自平衡试桩法桩土荷载传递机理原位测试[J].岩土力学,2003,24(6):96-101
Analysis of Single Pile Bearing Performance Based on O-cell Test Results of Piles
LIU Jianglei
2016-10-19
刘江磊(1984—),男,2010年毕业于中国地质大学地质工程专业,工学硕士,工程师。
1672-7479(2016)06-0063-04
TU473.1+1; TU413.4
A
