高中物理电场叠加问题的解题技巧

江西省金溪县第一中学 许涛涛

高中物理电场叠加问题的解题技巧

江西省金溪县第一中学 许涛涛

高中物理中，电场叠加问题十分重要，是高考经常涉及的知识点。由于电场叠加问题十分抽象，因此很多学生在学习过程中会觉得有些困难。本文主旨是分析高中物理电场叠加问题的解题技巧。

高中物理 电场叠加 解题技巧

一、叠加场简介

场的含义主要是指空间中物体的分布情况，而叠加场就是指多中场并列存在的同一个区域内，如磁场、重力场和电场等。电力场叠加问题中，比较常见的就是叠加场中的运动问题。这类问题往往涉及很多知识点和空间想象力，还涉及物体的运动状态，如匀加速运动、圆周运动和曲线运动等，计算中还会考察学生的计算能力，所以这类题目具有较强综合性，解题时需要综合运用所学知识，才能更好地解答题目。

二、例题

例题1：半径为R的绝缘球壳上均匀地带有电量为+Q的电荷，另一带电量为+q的点电荷放在球心O上，由于对称性，点电荷受力为零，现在球壳上挖去半径为r（r＜ R）的一个小圆孔，则此时置于球心的点电荷所受力的大小为？（已知静电力恒量为k）

这道题目一共有两种解法。第一个解法如下：利用“补偿法”求解。在球壳上挖一小圆孔，相当于圆孔处放一等量异种电荷，电量为:，因为挖去小孔前受力平衡，所以挖去后受力即为q'与q的库仑力。即，方向由球心指向小孔中心。第二种解法如下：本题还可以等效为在挖去一小圆孔的关于球心对称的另一侧放一等量同种电荷q'，对球心处的q产生的电场力，因，且它与q是同种电荷，所以，方向仍由球心指向小孔中心。

我们通过这道题目可以看出，求解电场强度时可通过对研究对象进行分割或补偿，从而使非理想化模型、非对称体转化为对称体，达到简化结构的目的，进而算出题目。

例题2： 如图所示，均匀带电圆环的带电荷量为＋Q，半径为R，圆心为O，P为垂直于圆环平面的对称轴上的一点，OP＝L，P点的场强为多少?

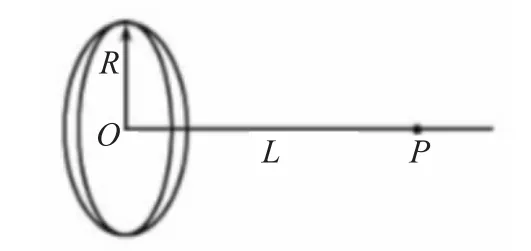
可以利用为微元法解题，也就是在圆环位置处截取一段设为Δl，用P表示圆环位置电荷分布密度，那么p×Δl则为此段的带电量，即Δq，则为P点场强，用E表示，已知r²＝ R²＋L²，那么还可以用Ex＝Ecosθ，cosθ＝，Ey＝ Esinθ。分解P点处场强，圆环位置处的电荷有对称性的分布特点，由此可知，Y轴合电场是0。那么就可以用ΣEx＝表示P点场强，即Ep。这道题目主要应用的是微元法进行解题。

例题3：如图所示，在半径为R的圆环上分布有不能移动的正电荷，总电量为Q，AB是它的一直径，如果要使AB上的场强处处为零，问圆环上的电荷应该如何分布？

解题方法如下：由对称性可知均匀分布的圆环圆心处的场强为0，由此可推广：均匀带电球壳其内部场强处处为0。由于要求直径AB上的场强为0，而圆环只对圆心具有中心对称性，故可知圆环上的电荷分布是不均匀的，可设想把原均匀分布在球面上的电荷，对应地压缩到以AB为直径的一圆环上，它们在直径AB上的场强则处处为0。

如图所示，圆环上任一点P处一段弧长ΔL，ΔL上的电量应等于半径为R，电量为Q的均匀带电球面上相应一小环带所带电的一半有，ΔL即圆环上电荷分布规律为：

通过这道题目可以看出，将圆环上电荷的分布不均匀、球面上的电荷的均匀分布联系起来，是解开本题的重要步骤。而这种联系是建立在两者于直径上的场强等效而产生的，静电学的等效处理在解答这类习题时十分有效。

以上三道题目不难发现，在计算电场叠加问题时有一些固定的公式和办法，为了更好方便学生在题目中的应用现对这些方法进行总结。第一种是最基本的解题方法，通常要遵循平行四边形定则（矢量合成）进行解题。第二种方法就是对称法，就是利用一些物理现象、物理规律，或者图形自身的一些对称性进行解题。利用这些现有的规律和性质能够省去很多复杂的计算环节，让题目变得更加容易。第三种方法就是例题中提到的补偿法，这种方法通常应用与题目中题目中所给的条件不够完整，但是要解开题目又必须要建立模型，这时候就需要用到补偿法，需要利用原有的条件补充出一些新的条件，构建完整的模型，再去解答题目，不要忘记新模型是补充了条件的，最后要记得减去补充条件的差值。第四种方法是微元法。这种方法就是将研究对象分割，变成很多微小的部分，然后针对微小的部分进行分析。从而使一些比较难求的量转化成比较容易确定的量甚至转换成常量。从而使题目的解答变得更加容易。第五种方法是极值法。在物理题目中经常会应用到数学知识和数学技巧。所以物理题目中也会涉及极值问题，这时候就可以利用数学中解答极值问题的技巧来解决相关问题。最后一种则是等效替代法，实现类似条件之间的转换。例如，ABC之间，从A的事实出发，然后论证B的事实可以代替A，然后如果需要在由B到C知道出现需要的解决问题的条件。也可以用模型代替实物，或者以合力代替分力等。这种方法就是利用本质相似或相近的物体或条件，进行替换最后解答题目的方法，经常是用简单的因素或条件代替复杂因素或条件。

ISSN2095-6711/Z01-2016-12-0217