无刷直流外转子电机结构参数优化

刘志强

舒刚华1

杜荣华1

杨中华2

(1. 长沙理工大学汽车与机械工程学院，湖南 长沙 410114；2. 长沙中成汽车零部件有限公司技术部，湖南 长沙 410114)



无刷直流外转子电机结构参数优化

刘志强1

舒刚华1

杜荣华1

杨中华2

(1. 长沙理工大学汽车与机械工程学院，湖南 长沙 410114；2. 长沙中成汽车零部件有限公司技术部，湖南 长沙 410114)

齿槽转矩脉动是影响直流外转子电机输出转矩脉动的主要原因。为抑制齿槽转矩脉动，根据电机的结构参数建立了有限元分析模型，并对齿槽转矩进行仿真；仿真结果与试验获取的齿槽转矩曲线吻合较好，证明了所建模型的正确性。然后，采用Taguchi方法，以齿槽转矩峰值和平均输出转矩作为优化目标，以槽口宽度、极弧系数、气隙长度、平行齿宽为控制因子，选取槽口宽度加工误差、气隙长度加工误差、平行齿宽加工误差和永磁体剩磁变化作为噪声因子，对电机进行了优化设计，并利用所建立的有限元分析模型进行性能仿真验证。结果表明：用Taguchi方法优化电机设计参数，能够在电机平均输出转矩略有增加的同时，显著降低齿槽转矩。

优化设计；Taguchi方法；齿槽转矩；直流外转子电机；有限元分析

永磁无刷直流外转子电机正获得越来越广泛的应用。电机外转子与驱动系统直接相连，可使结构更加简单、紧凑、高效。然而，永磁无刷直流外转子电机转矩波动大，直接驱动方式对电机提出了更高的要求——输出转矩大，转矩脉动低，调速范围宽[1]，所以需要优化设计以提高其性能指标。抑制齿槽转矩脉动而不降低电机平均输出转矩是永磁直流电机研究的主要内容之一。从电机设计角度出发，其方法通常包括：磁极偏移、斜槽和斜极、不等气隙、优化磁极极弧宽、磁极分段错位、采用分数槽绕组、虚拟样机等方法[2-6]。传统的方法在分析电机设计中的非线性耦合问题时，往往会出现以下问题：① 全局优化方法计算时间太长，可能得不到全局最优解；② 局部优化方法的优化对象和目标有限，求解多目标优化问题时比较乏力，往往容易忽视噪声因素对电机性能的影响，因此其优化结果与实际产品的性能有着不容忽视的差异。

Taguchi方法[7]是依据统计学原理、方法，利用正交试验法来安排试验的一种参数优化设计方法，可以用较少的试验时间和成本获取需要的试验结果。目前，Taguchi方法已应用于转子系统动力学[8]、冲压工艺参数[9]、动力总成悬置[10]、柔性铰链柔度[11]等方面，但在电机优化设计方面鲜有报道。

本试验提出采用Taguchi方法，在不采取提高工艺水平、改善材料品质的前提下，考虑多目标优化问题，以齿槽转矩峰值最小、平均输出转矩最大为目标，以对齿槽转矩峰值和平均输出转矩影响较大的参数作为控制因子，同时考虑加工误差等噪声因子对优化设计的影响，对无刷直流外转子电机进行优化设计。

1 电机有限元模型的建立

1.1 齿槽转矩的测量

采用步进电机法测量了一台无刷直流外转子电机的齿槽转矩。通过联轴器将步进电机、转矩传感器、被测电机联接。用步进电机控制器控制脉冲数，使步进电机精准地转过一定角度。由于被测电机的齿槽转矩作用，试图使转子定位在某一个位置，而步进电机转过一个角度后本身存在一个保持转矩，让传感器的一端定位在当前的位置，成为一个固定端。这样外转子电机的齿槽转矩就直接作用在传感器上，从数据采集设备中可以直接获取[12]。

1.2 有限元分析模型的建立

无刷直流外转子电机的基本结构参数见表1。其定子槽结构见图1，尺寸为：Bs0=2 mm，Hs0=1.3 mm，Bs1=6.5 mm，Bs2=4.9 mm，Hs2=16 mm。

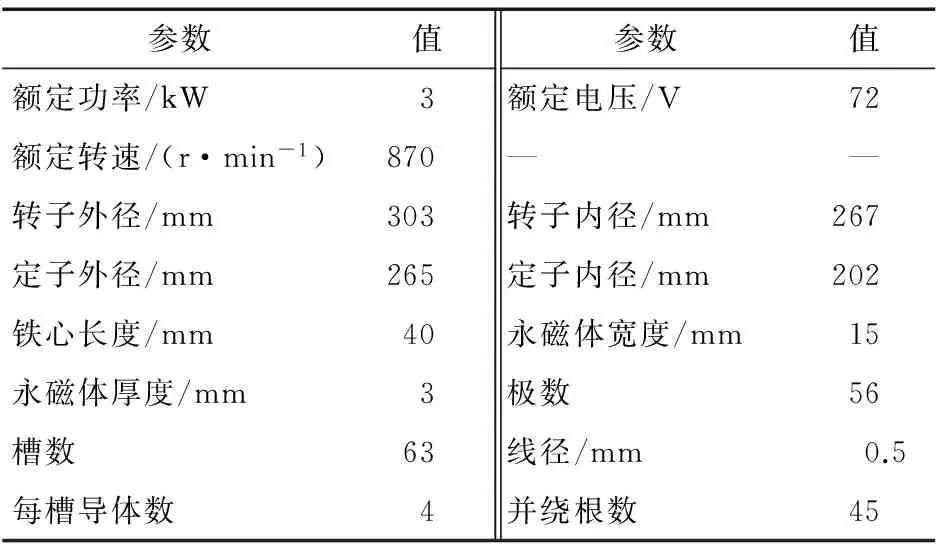
表1 电机基本参数Table 1 Parameters of an external rotor motor

在Maxwell 2D中建立有限元分析模型，调整相应的仿真设置(如漏磁系数、步长、能量误差、网格大小)，对比所测量的齿槽转矩曲线，使仿真结果和试验数据能够较好匹配，得到分析模型见图2，仿真结果见图3。

图1 定子槽结构Figure 1 Structure of stator slot

图2 电机有限元分析模型Figure 2 Finite element analysis model of the motor

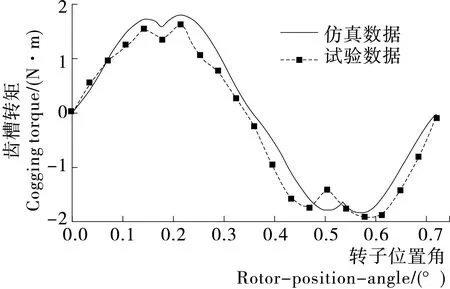
图3 齿槽转矩仿真曲线和测试曲线对比Figure 3 Comparison of cogging torque between simulation and test value

2 基于RMXPRT的参数化分析

本试验主要对电机的本体结构进行优化设计以抑制转矩脉动，主要是减少齿槽转矩。永磁无刷直流外转子电机的齿槽转矩表达式为[13]：

(1)

式中：

Tcog(α)——齿槽转矩，N·m；

La——电枢铁心轴向长度，mm；

μ0——空气磁导率，H/m；

R1——定子轭外半径，mm；

R2——转子内半径，mm；

z——定子槽数；

Gn——与定子槽数、槽口宽度、气隙长度等有关的傅里叶展开式系数；

Brm——与极弧系数、永磁体剩磁等有关的傅里叶展开式系数；

α——定转子之间的相对位置角，rad。

利用RMXPRT软件对式(1)中的各参数进行分析，确定各参数对电机平均输出转矩和齿槽转矩的影响大小及参数合理取值范围。以永磁体极弧系数为例，首先将极弧系数设为变量arc，取值范围为0.5～1.0，步长为0.01，以齿槽转矩峰值和平均输出转矩为求解参数，得到的曲线见图4、5。

由图4、5可知：平均输出转矩随极弧系数的增大而单调增大，这是因为极弧系数增大后，永磁体宽度增大，使气隙磁通量增大，从而导致输出转矩增加。而齿槽转矩峰值随着极弧系数的增大呈波动变化，最小值出现在极弧系数约为0.57和0.64处。这说明同时对电机的平均输出转矩和齿槽转矩优化时，需要对极弧系数进行慎重选择。同理可得到其它对电机齿槽转矩和平均输出转矩影响较大的参数及其变化范围，用于Taguchi方法的参数水平确定。

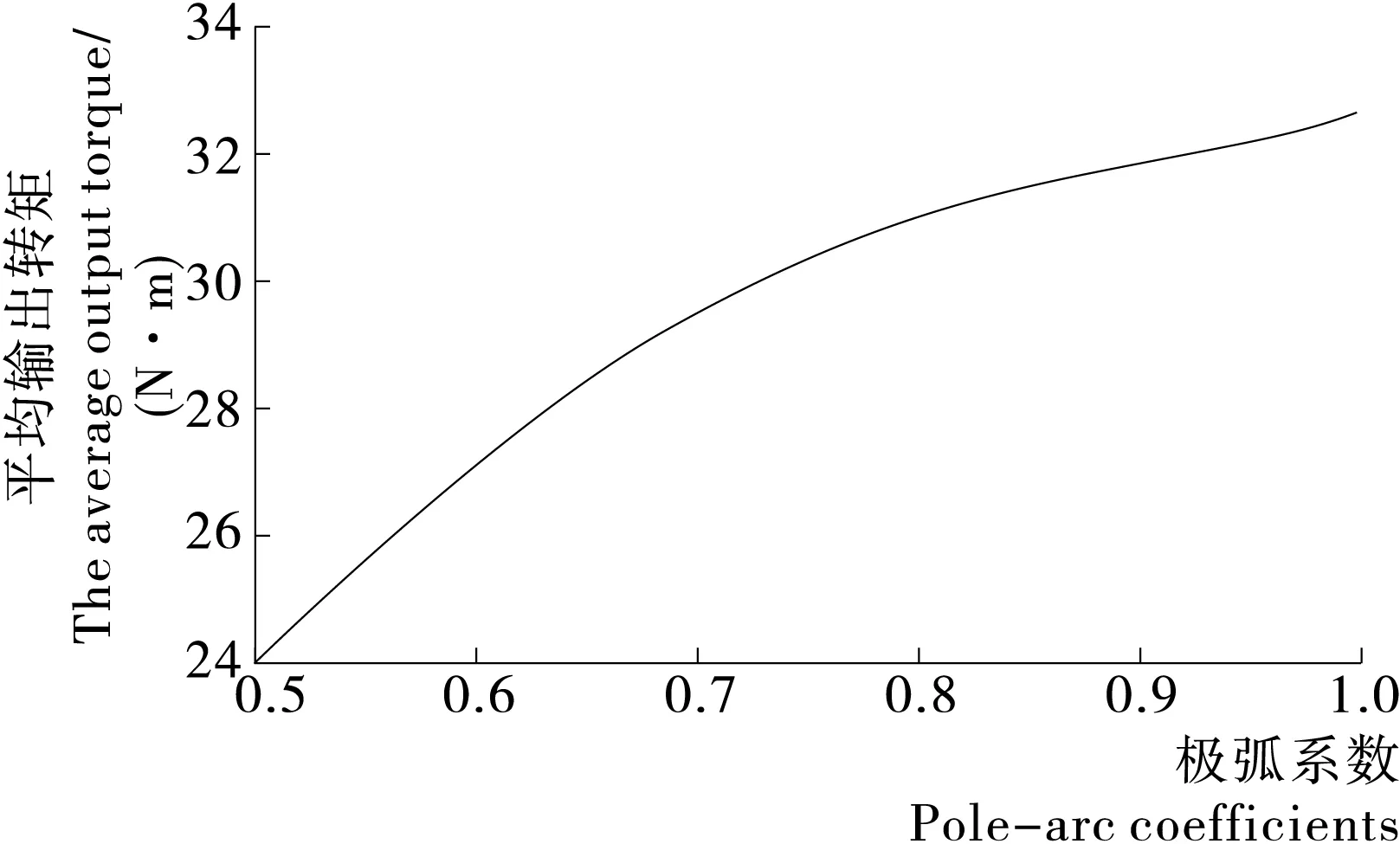
图5 平均输出转矩随极弧系数的变化曲线Figure 5 Relationship of average output torque with pole-arc coefficient

3 基于Taguchi方法的电机优化设计

3.1 确定控制因子和噪声因子

通过对影响电机齿槽转矩和平均输出转矩的各结构参数进行参数化分析，结合参数变量允许的变化范围，确定槽口宽度bs、永磁体极弧系数αp(αp=l/τ)、气隙长度δ、平行齿宽bt作为可控因子，每个因子水准的取值见表2。

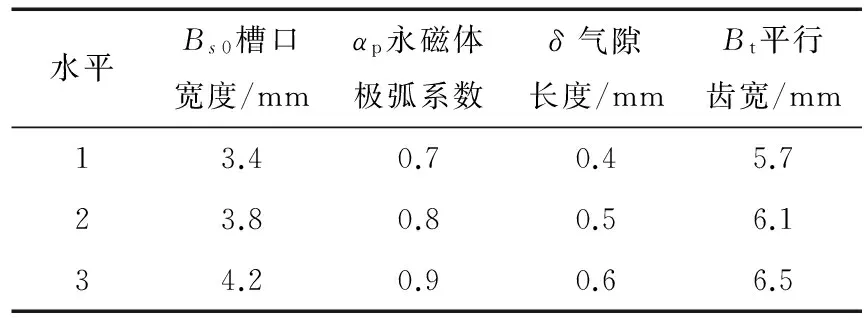
表2 可控因子取值水平表Table 2 Value level of the controlled factor

考虑到所选的控制因子及加工误差、材料变化等因素，选取的噪声因子为槽口宽度加工误差ΔBs0、永磁体剩磁偏差ΔBr、气隙长度加工误差Δδ、平行齿宽加工误差ΔBt。各因子的水平值见表3。对于其它环境因素、材料性能变异等噪声因子不做单独考虑，假设其影响已包含在各参数的取值变化范围内。

表3 噪声因子取值水平表Table 3 Value level of the noise factor

3.2 进行正交试验

由表2、3可知，控制因子、噪声因子都为4因子3水平，若改变一个参数进行一次试验并进行有限元分析，则需要进行6 561次试验。若根据选取的控制因子及其水平值选取内表，根据选取的噪声因子及水平值选取外表，将内外表组合确定试验方案(表4)，则只要进行81次有限元分析，大大降低了优化设计所耗时间。

根据表4所示的表头安排试验，用ansoft对各种参数组合进行有限元分析，得到电机平均输出转矩Ta和齿槽转矩峰值Tc(见表5、6)。

3.3 数据分析

先根据平均输出转矩和齿槽转矩峰值的期望特性得到相应的信噪比计算公式，然后运用统计学方法，进行均值分析、方差分析，得到各控制因子对平均输出转矩和齿槽转矩峰值的影响大小。

3.3.1 信噪比分析 信噪比(sigal-to-noise ratio, SNR)是Taguchi优化方法的重要工具，是评价参数设计优劣的指标。信噪比定义式为：

表4 正交试验表头设计Table 4 Orthogonal experiment table

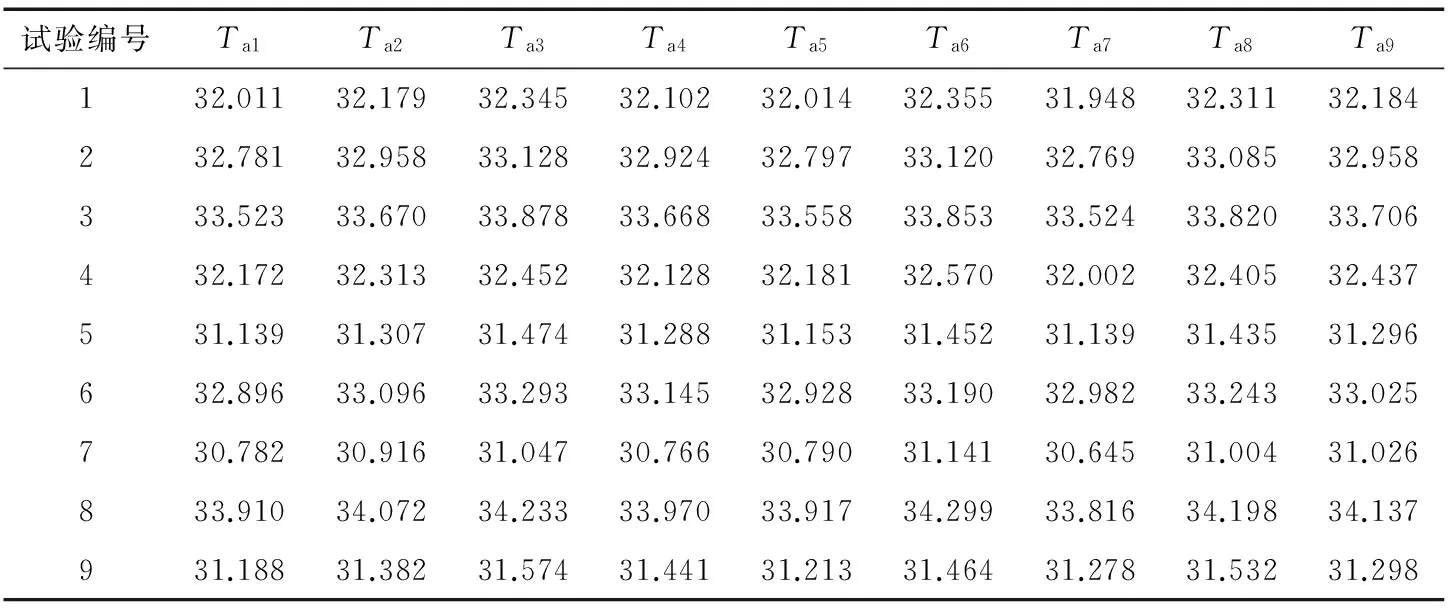
表5 Ta有限元分析值Table 5 Results of Ta by finite element analysis N·m

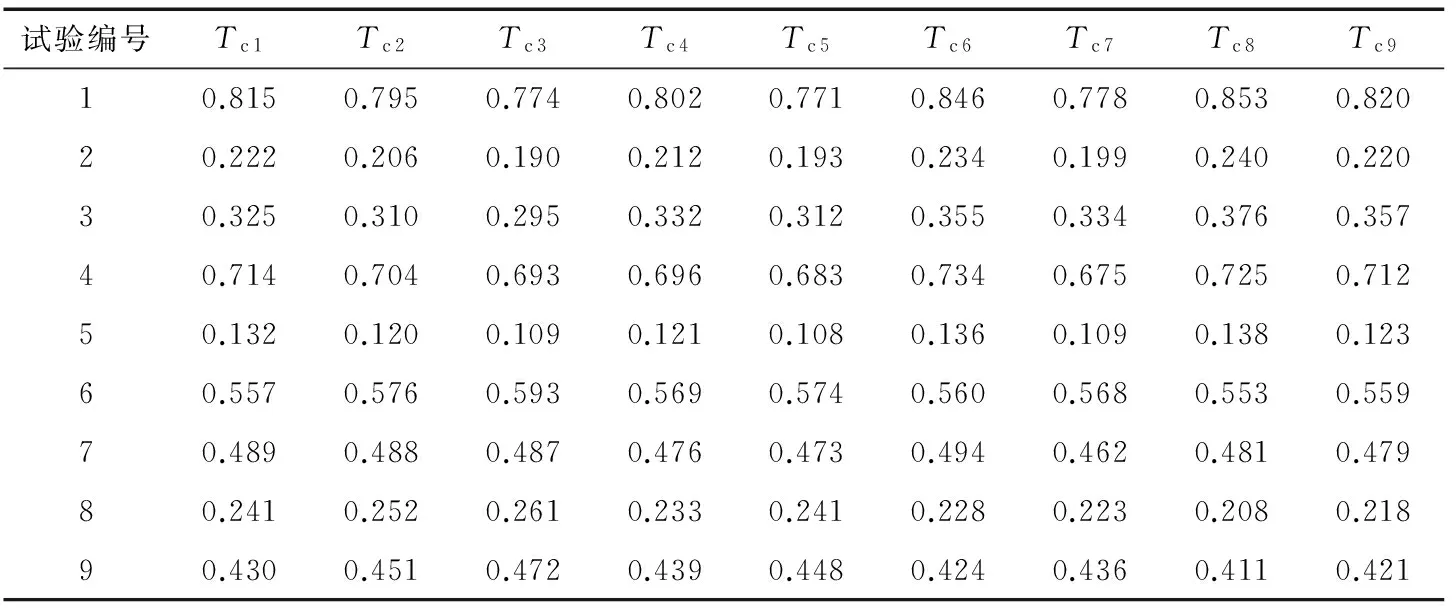
表6 Tc有限元分析值Table 6 Results of Tc by finite element analysis N·m

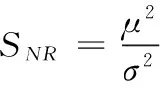
(2)

式中：

SNR——信噪比

μ——产品输出特性yi的期望，

σ2——产品输出特性yi的方差。

电机的平均输出转矩表现为典型的望大特性，而齿槽转矩峰值表现为典型的望小特性。即期望平均输出转矩的均值越大越好，方差越小越好，而齿槽转矩峰值的均值和方差都越小越好。

望小特性的信噪比表达式：

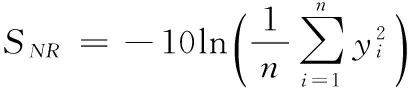
(3)

式中：

n——同一试验编号下获取的产品某一输出特性的试验数据的个数。

望大特性的信噪比表达式：

(4)

利用式(3)和式(4)分别计算齿槽转矩峰值和平均输出转矩的信噪比，得到的结果见表7。

3.3.2 均值分析 计算不同可控因子在不同因子水平下的Ta与Tc信噪比的平均值，结果见表8。

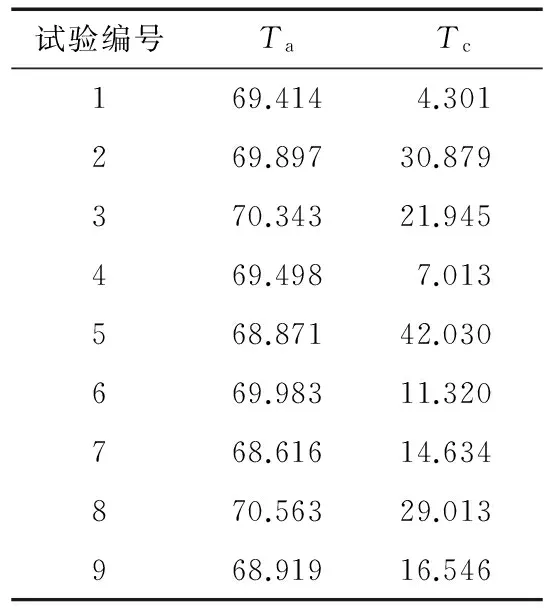
表7 平均输出转矩Ta和齿槽转矩峰值Tc的信噪比Table 7 Signal-to-noise ratio of Ta and Tc dB

由表8可知：控制因子Bt对Ta的影响最大，αp对Tc的影响最大。若要以平均输出转矩最大为优化目标，则选取的最佳参数组合为Bs01(3.4 mm)、αp2(0.8)、δ1(0.4 mm)、Bt3(6.5 mm)；若以齿槽转矩峰值最小为优化目标，则选取的最佳参数组合为Bs03(4.2 mm)、αp2(0.8)、δ3(0.6)、Bt1(4.7 mm)。

3.3.3 方差分析 方差分析主要通过分析研究不同参数的改变对电机性能参数的贡献大小，来确定控制因子在电机优化设计中所占比重大小。各参数总的方差的计算公式：

表8Ta与Tc在不同控制因子及水平下的信噪比平均值

Table 8 Mean value of signal-to-noise ratio ofTaandTcunder different control factors and levels

dB

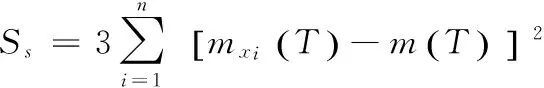
(5)

式中：

x——Bs0、αp、δ、Bt控制因子；

T——电机的性能指标，指Ta或Tc；

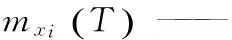
m(T)——Ta或Tc的平均值。

方差计算结果见表9。

表9 各个参数对性能参数的影响Table 9 Influence of design parameters on performance

由表9可知，Bs0、δ、Bt在Ta中所占比重比Tc中所占比重大，αp在Tc中所占比重比Ta中大。因此若同时考虑平均输出转矩和齿槽转矩峰值，则选取的最佳参数组合为Bs01(3.4 mm)、αp2(0.8)、δ1(0.4 mm)、Bt3(6.5 mm)。

3.3.4 优化结果仿真验证 利用前面建立的Maxwell 2D模型，改变相应的设计参数取值，对选取的最佳参数组合进行有限元仿真验证，得到的齿槽转矩曲线和转速稳定后的输出转矩曲线分别见图6、7。

由图6可知，优化后的齿槽转矩峰值约为0.8 N·m，优化前的齿槽转矩峰值约为2.3 N·m，通过优化设计大大减小了齿槽转矩的峰值；由图7可知，优化前的输出转矩在23.0～37.5 N·m，优化后的输出转矩在27.5～36.5 N·m，通过优化设计明显降低了转矩脉动。同时由仿真分析的结果可知，优化前的平均输出转矩约为33.6 N·m，优化后的平均输出转矩约为33.8 N·m。

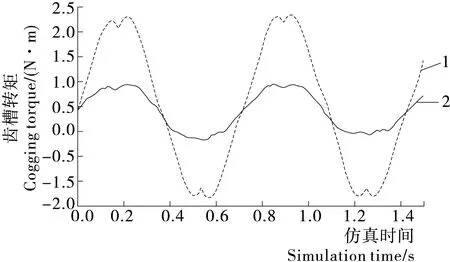
1. 优化前 2. 优化后图6 优化前后齿槽转矩波形图Figure 6 Waveform of cogging torque

图7 优化前后输出转矩波形Figure 7 Waveform of output torque

由上述分析可知，经过Taguchi方法优化后的电机，齿槽转矩降低了约2/3，转矩脉动情况也有明显改善。同时平均输出转矩略有增加，达到了优化设计目的。

4 结论

(1) 建立了无刷直流外转子电机的有限元分析模型，并以试验获取的齿槽转矩曲线加以验证；并对影响电机齿槽转矩和输出转矩的各结构参数进行了敏感性分析，确定了控制因子。

(2) 采用Taguchi方法，对电机进行了优化设计。性能仿真结果表明，齿槽转矩显著降低，转矩脉动明显改善，同时平均输出转矩略有增加。研究发现，在不改进加工工艺、使用高性能的材料的前提下，采取各设计参数的优化来实现电机的稳健设计，在电机的多目标局部优化中有重要的工程应用价值。

[1] YOSHIMURA M, FUJIMOTO H. Driving torque control method for electric vehicle with in-wheel motors[J]. Electrical Engineering in Japan, 2012, 181(3): 49-58.

[2] METIN A, MEHMET G. Reduction of cogging torque in double-rotor axial-flux permanent-magnet disk motors: a review of cost-effective magnet-skewing techniques with experimental verification[J]. IEEE Transactions on Industrial Electronics, 2014, 61(9): 5 025-5 034.

[3] WANG Dao-han, WANG Xiu-he, YANG Yu-bo, et al. Optimization of magnetic pole shifting to reduce cogging torque in solid-rotor permanentmagnet synchronous motors[J]. IEEE Transactions on Magnetics, 2010, 46(5): 1 228-1 234.

[4] CLAUDIO B, FABIO I, EMILIO L, et al. Review of design solutions for internal permanent-magnet machines cogging torque reduction[J]. IEEE Transactions on magnetics, 2012, 48(10): 2 685-2 693.

[5] WOO D K, KIM I W, LIM D K, et al. Cogging torque optimization of axial flux permanent magnet motor[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2 189-2 192.

[6] 毛文贵, 傅彩明, 谭加才. 基于虚拟样机技术的立式电机结构设计分析[J]. 食品与机械, 2006, 22(4): 67-69.

[7] TAGUCHI G, CHOWDHURY S, WU Yin. Taguchi's quality engineering handbook[M]. New Jersey: John Wiley Publication, 2004: 125-169.

[8] 杨隽, 臧朝平, 刘永泉, 等. 基于Taguchi方法的转子系统动力学容差设计[J]. 航空动力学报, 2014, 29(7): 1 583-1 590.

[9] 王卫洪. 基于田口方法的冲压工艺参数稳健性设计[J]. 模具制造, 2015(12): 10-16.

[10] 张代胜, 张旭, 王浩, 等. 基于Taguchi方法的动力总成悬置系统稳健优化 [J]. 汽车工程, 2014, 36(4): 475-480.

[11] 伍建军，万良琪，吴事浪, 等. 基于田口方法的柔性铰链柔度稳健优化设计[J]. 工程设计学报, 2015, 22(3): 224-229.

[12] 冯兆冰, 吴孔圣, 丁云飞, 等. 几种简单的齿槽转矩测量方法[J]. 制造技术与机床, 2012(5): 102-103.

[13] 王秀和. 永磁电机[M]. 北京: 中国电力出版社, 2007: 80-81.

Optimal design on a brushless DC external rotor motor

LIU Zhi-qiang1

SHUGang-hua1

DURong-hua1

YANGZhong-hua2

(1.SchoolofAutomotiveandMechanicalEngineering,ChangshaUniversityofScienceandTechnology,Changsha,Hunan410114,China; 2.ChangshaZhongchengAutomotiveComponentsCo,Ltd,Changsha,Hunan410114,China)

Cogging torque ripple is the main impact factor of the output torque ripple of electric vehicles driven by wheel hub motors. To suppressing cogging torque ripple, a DC external rotor motor was studied, and a finite element analysis model was established in Ansoft Maxwell according to its structural parameters. The simulation results of cogging torque agreed well with those obtained from experiments, and this showed the analysis model was correct. Then, the main parameters of the hub motor were optimized by using Taguchi method, in which the peak values of cogging torque and average values of output torque were taken as the optimization goals, the slot width, pole arc coefficient, air gap length and parallel tooth width as the control factors, the processing errors of notch width, air gap length and parallel tooth width, and residual magnetism variation as noise factors. The performances of the motor were simulated in the finite element analysis model with optimal structural parameters. The results showed that the cogging torque of the motor was reduced significantly, and the average values of output torque were increased slightly at the same time.

optimal design; Taguchi method; cogging torque; DC external rotor motor; finite element analysis

国家自然科学基金(编号：11572055)；交通运输部基础应用研究项目(编号：2013319825090)；长沙市科技局项目(编号：K1301006-11)

刘志强(1970-)，男，长沙理工大学副教授，博士。 E-mail:lzq0228@126.com

2016-09-21

10.13652/j.issn.1003-5788.2016.11.021