基于模糊PID控制的电磁式定量给料系统

戚 俊

龚大伟1

李 燕

闫清泉

(1. 中国科学院合肥物质科学研究院应用技术研究所，安徽 合肥 230088；2. 中科院合肥技术创新工程院，安徽 合肥 231283)



基于模糊PID控制的电磁式定量给料系统

戚 俊

龚大伟1

李 燕

闫清泉

(1. 中国科学院合肥物质科学研究院应用技术研究所，安徽 合肥 230088；2. 中科院合肥技术创新工程院，安徽 合肥 231283)

为解决传统电磁式定量给料系统开环控制过程中给料速度设定随意性较大，无法根据智能控制策略动态调节给料速度的问题，提出并设计了一种基于模糊PID控制的电磁振动定量给料系统；设计了系统整体机械结构，通过理论分析得到了可控硅导通角与振幅的数学关系；并在此基础上建立了简化的电磁振动给料机二阶数学模型。仿真试验结果表明，该系统动态跟随性较好、控制精度较高、响应速度较快和鲁棒性较高，具有较好的应用前景。

电磁振动给料机；模糊PID；给料速度；

电磁式定量给料系统由于结构简单、能耗低、可靠性高、可控性良好等优点被广泛应用于定量给料和大剂量颗粒食品自动包装领域[1][2]1-2。目前中国的颗粒食品定量给料系统给料速度大多为开环控制，现场通过人工调节电磁铁激振电压的方式调整给料速度[3-4]，由于每台给料设备的差异导致每台设备相同的给料速度对应的激振电压不一致，速度给定的随意性较大，无法实现在给料过程中给料速度的动态调节。此外，电磁振动给料系统的出料速度受物料性状、机械安装和器件性能偏差的影响，并在系统长期工作中机械特性和控制特性会因机械振动和器件老化等因素产生变化[5]，因此电磁振动给料系统为多参数时变系统。

传统的PID控制器对于一个模型固定的系统具有结构简单、性能可靠等优点[6]，参考文献[6～7]提出并设计了基于PID控制的电磁振动给料系统，但是由于电磁振动给料机的参数的时变性，一组固定的PID参数无法满足系统应用要求；参考文献[5]和[8]24-34分别基于振幅自适应算法和模型自适应算法设计了电磁振动给料的智能控制系统，能较好的动态适应和调整相关控制参数，由于该智能算法较为复杂，实际工程应用难度较大。

模糊PID控制是一种将传统PID控制与模糊控制理论相结合的一种控制算法，在不需要掌握被控对象准确的数学模型情况下,根据设定的模糊规则自适应调整PID控制器参数，因其较显著的改善传统PID控制器的控制性能而被广泛应用于各种工业控制领域[9]。为提高电磁式定量给料系统的给料效率，改善传统电磁式定量给料系统控制性能的不足，实现给料过程中给料速度根据给料策略动态调节，设计了一种基于模糊PID控制的电磁式食品定量给料系统。

1 电磁式食品定量给料系统及其原理

电磁式食品定量给料系统是一种利用电磁振动给料的基本工作原理结合智能控制算法设计的智能定量给料系统。系统的机械结构图见图1。

系统整个给料过程根据智能给料策略实行二级给料[10]，即在给料过程初期以较快的速度给料，在给料过程后期以较慢速度给料，以兼顾给料速度和给料精度。系统启动后电磁铁2吸引旋转出料盘1做受迫振动，物料通过旋转出料盘1导料槽输送到称重斗3内，通过对称重斗内颗粒食品重量变化率的计算得到实时出料速度。当颗粒食品在正常出料状态时，根据物料输送的进程和相关参数给定，系统动态调节施加在电磁铁上的激振电压，实现对整个给料过程的动态调节和智能化控制；当系统工况出现异常或称重斗内颗粒食品超过允许范围，系统控制挡板开合将本次物料导入物料回收仓内并重新给料。

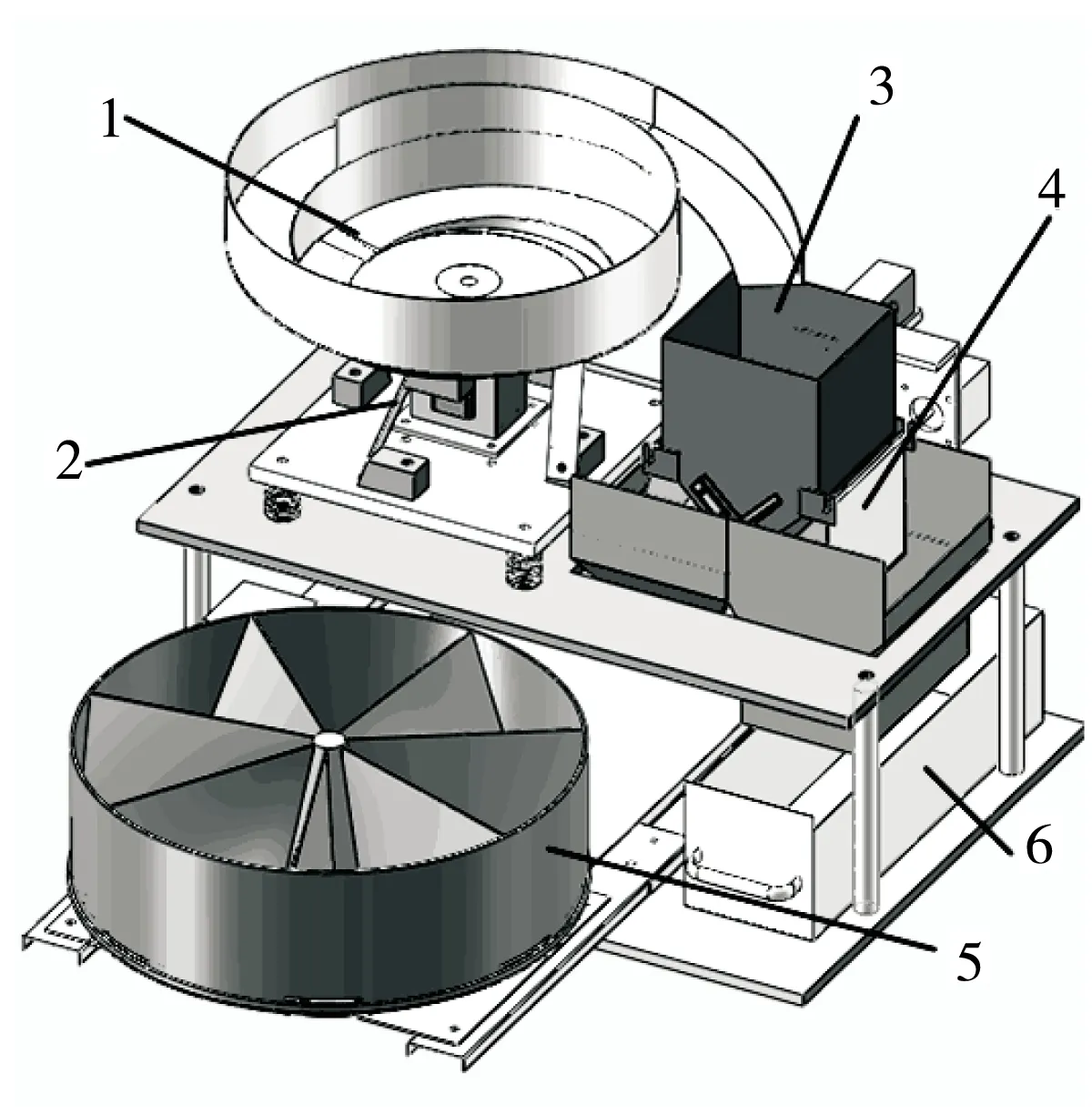
1. 旋转出料盘 2. 电磁铁和弹片 3. 称重斗 4. 导料挡板 5. 旋转接料盘 6. 物料回收仓

图1 电磁式食品定量给料系统机械结构图

Figure 1 Electromagnetic food quantitative feeding system mechanical structure

2 电磁振动给料器数学模型

为便于数学分析，将电磁振动给料器力学模型抽象成图2 所示的二自由度双质体受迫振动系统，图2中m1为振动出料盘和物料的折算总重量(kg)，m2为底座的折算重量(kg)；c表示振动出料盘与底座之间的相对阻尼系数，c1和c2分别为振动出料盘和底座的绝对阻尼系数；k为主振弹簧刚度(N/m)，k2为减振弹簧刚度(N/m)；S1、S2分别为振动出料盘和底座沿振动方向上的位移(m)；F(t)为接料盘收到的电磁吸引力(N)[2]21-22[8]18-20。

根据牛顿第二定律可得振动过程中的微分方程为：

(1)

图2 电磁振动给器力学模型Figure 2 Electromagnetic vibration to the mechanics model

忽略绝对阻尼和减振弹簧的刚度，将(1)式简化变形得到：

(2)

式中：

S——相对位移(S=S1-S2)，m。

对于电磁力为周期波力F(t)=Fsin(ωt+φ)有：

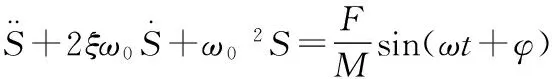
(3)

式中：

ω——周期力波的频率，Hz；

F——周期波力的幅值，N。

设式(3)的特解为：

S=λsin(ωt+φ-α)。

(4)

求解得：

(5)

式中：

z0——电磁激振力频率与系统固有频率比；

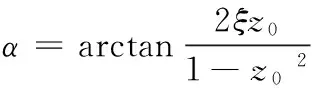
忽略绝对阻尼和减振弹簧的刚度得：

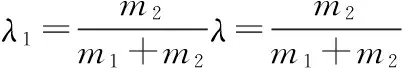
(6)

式中：

λ1——振动出料盘的绝对振幅，m。

3 给料速度与导通角关系

对于半波整流方式下系统的主电路见图3。

电能经过电磁铁转换成机械能输出，带动振动机构出料，考虑主电路中电磁铁感抗远远大于阻抗，电流表达式为：

(7)

解微分方程得：

(8)

根据电磁学理论，电磁铁磁密表达式为：

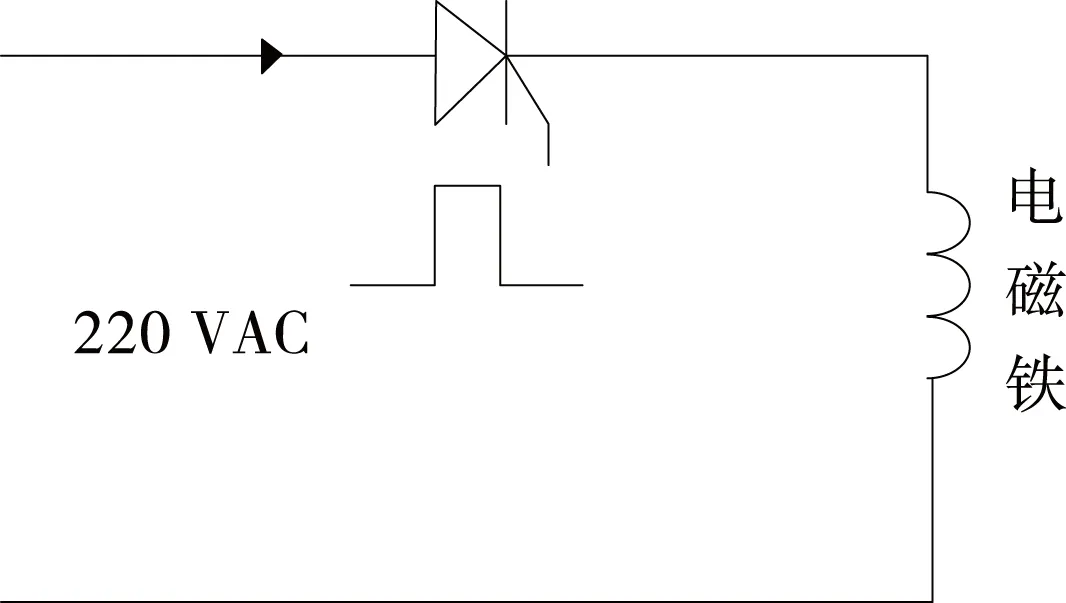
图3 半波整流主电路图Figure 3 Half-wave rectifier main circuit diagram

(9)

结合电磁铁吸合力公式F=b2S/2μ0，得：

f(ε,t)=

(10)

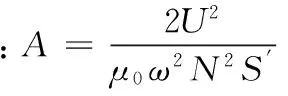
在电磁振动给料系统中，固定吸力只能产生静形变，对系统振幅不产生影响；二次谐波力偏离了振动点，对于系统振幅产生的作用可以忽略；故对系统振幅产生直接影响的只有一次谐波力，通过富氏级数对电磁铁吸合力表达式进行展开[11]，得一次谐波力系数为：

(11)

(12)

一次谐波力的幅值表达式为：

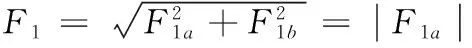
(13)

联系式(13)可得可控硅触发角ε与振动出料盘绝对振幅之间的数学关系为：

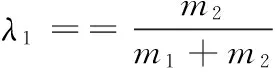
(14)

由于式(14)中参数随时间变化缓慢，在一次控制过程中近似为常数，可以得系统的导通角2π-2ε与振动出料盘的绝对振幅的相对关系见图4。

图4 导通角与振幅关系曲线Figure 4 Conduction Angle and amplitude relation curve

由图4可知：当导通角在[0°,150°)区间内时，振幅很小几乎不能实现出料，在实际控制过程中系统不运行在这段区间；当导通角在(300°,360°]区间内时，系统输出振幅很大，但是由于此时系统进入饱和状态，系统的功耗很大；同时考虑衔铁与磁芯之间易发生碰撞，系统的机械特性会变坏，减少系统寿命，因此在实际控制过程中系统也应当避免运行在此区间内；当导通角在[150°,300°]区间时系统的振幅在较大范围内连续可调，并与导通角表现为近似一次函数关系，可以满足系统控制需求并具备良好的控制性能。电磁振动给料系统平均出料速度理想的振幅区间应使得物料只有正向滑行，出料速度与振幅成正比关系[12]。

基于上述分析，在系统平稳运行情况下，从导通角到出料速度为近似二阶环节。

4 模糊PID控制器的构建

基于模糊PID控制的电磁振动定量给料控制系统结构框图见图5。

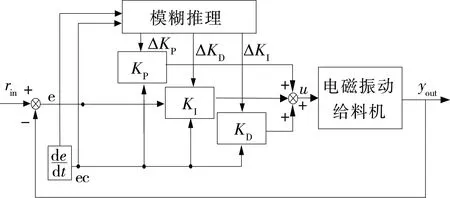
图5 电磁振动定量给料模糊PID控制系统Figure 5 Electromagnetic vibration feeding quantitative fuzzy PID control system

取系统速度输出yout与速度给定rin的误差e以及误差的变化率ec为控制系统输入，比例系数增量ΔKP、积分系数增量ΔKi、微分系数增量、ΔKD为模糊推理系统输出，构成一个两输入三输出的模糊推理系统，实现根据系统速度输出的结果动态自适应调整PID控制器的参数以改善传统PID控制器的控制性能[13]。

4.1 隶属度函数

模糊控制器的输入参量e和ec的实际论域范围分别为[-3,3]和[-9,9]；输出参量的ΔKP、ΔKI、ΔKD实际论域范围分别为：[-0.003,0.003]、[-0.03,0.03]、[-0.006,0.006]。将模糊控制的输入输出参量的模糊论域均设为E,EC,ΔKP,ΔKI,ΔKD={-3,-2,-1,0,1,2,3}其模糊集为:E,EC,ΔKP,ΔKI,ΔKD= {NB, NM, NS, Z, PS,PM, PB}, 其中元素NB、NM、NS、Z、PS、PM、PB 分别为负大、负中、负小、零、正小、正中, 正大。对于NB和PB元素的隶属度函数分别选择Z型和S型；其余元素隶属度函数选择三角形。模糊控制器输入输出参数隶属度函数设计见图6。

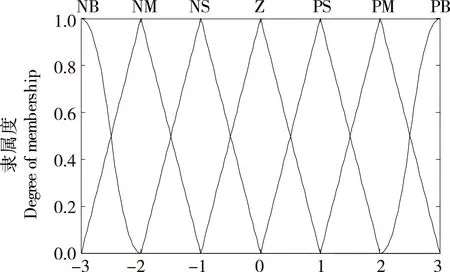
图6 模糊控制器输入输出参数隶属度函数Figure 6 The fuzzy controller input and output parameters of membership functions

4.2 PID参数自适应原则

(1) 当|e|较大时，为使系统快速响应应给KP较大的增量，同时根据ec情况给KI、KD适当的增量。

(2) 当|e|和|ec|较小，说明此时KP、KI、KD大小较合适，对3个参数不做调整。

(3) 当|e|较小，ec正向较大，针对增量式PID控制器，适当增加KI；ec负向较大，适当减小KI。模糊控制器推理规则见表1，输入输出关系见图7。

表1 KP、KI、KD模糊推理规则†Table 1 The fuzzy inference rules of KP, KI, KD

† 每格内从左至右分别为KP,KI,KD对应的模糊推理规则。

图7 模糊控制器输入输出对应关系Figure 7 Corresponding relations between input and output fuzzy controller

经过PID控制的实际参数KP、KI、KD计算公式见式(15)：

(15)

式中：

KP0、KI0、KD0——PID控制器初始值;

ΔKP、ΔKI、ΔKD——经过模糊控制器推理后得到的PID参数调整值。

5 模糊PID控制的电磁振动给料系统仿真

根据上述分析取电磁振动给料机激振导通角与给料速度的拉氏关系为：

F(S)=a/S2-b/S，

(16)

式中：

a、b——时变参数，不同系统由于安装偏差和老化程度不一致也不相同。

将式(16)带入构建好的模糊PID控制器中，在MATLAB环境下进行仿真试验；设系统参数a=1、b=3，给料速度设定为2，PID控制器初始值KP0=0.000 5，KI0=0.009 5，KD0=0；分别在模糊PID控制下和常规PID控制下系统响应给料速度情况见图8。

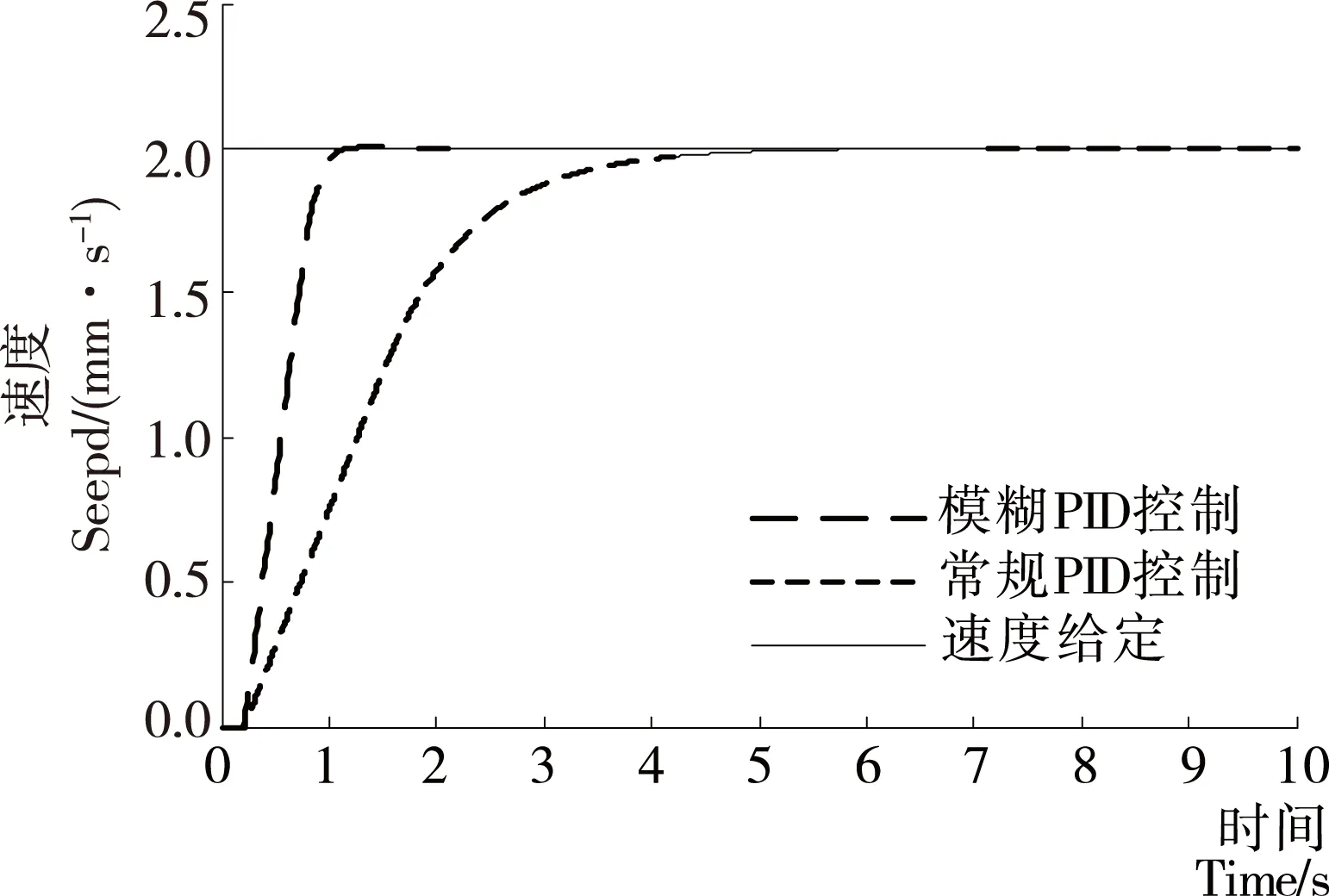
图8 模糊PID控制效果对比图Figure 8 The fuzzy PID control effect comparison chart

图8中水平实线为系统给料速度设定；虚曲线为常规PID控制下系统的响应曲线，实曲线为本文设计的模糊PID控制下系统的响应曲线。由图8可知：由于称重测量的滞后导致两条给料速度响应曲线均滞后0.2 s左右，在常规的PID控制下系统调节时间为5 s左右；本文设计的基于模糊PID控制的电磁振动定量给料系统调节时间为1 s左右并在此后稳定运行，几乎没有振荡和超调。

设系统参数a=0.9、b=3.15，给料速度前5 s设为2，后5 s设为1，模糊PID控制器初始值不变，模糊PID控制器推理过程和控制效果见图9。

图9 模糊PID控制器推理过程和控制效果Figure 9 Fuzzy PID controller reasoning process and the control effect

对比图9(d)与图8中模糊PID控制效果，可以看出：随着系统参数的改变，模糊PID控制针对不同给料速度设定具有较稳定的跟随性；由图9(a)～(c)可知：本研究设计的模糊推理规则具有较好的收敛性。从上述试验可以看出，基于模糊PID控制的电磁振动定量给料系统，其响应速度快，几乎没有振动和超调，运行性能良好。

6 结论

为解决传统电磁式定量给料系统无法根据智能给料策略动态调节给料速度的问题，本研究提出并设计了一种基于模糊PID控制的电磁式定量给料系统，仿真试验结果表明相对于常规PID控制，本系统能实现PID控制器参数自适应调整，控制精度良好且响应速度有了较明显提高；能根据智能给料策略动态调节给料速度，具有良好的应用前景。

[1] 闻邦椿, 刘树英. 振动机械的理论与动态设计方法[M]. 北京: 机械工业出版社, 2001: 3-4.

[2] 顾平灿. 电磁振动给料器的建模与参数选择[D]. 舟山: 浙江海洋大学, 2013.

[3] 骆有东. 电磁振动给料器的性能及控制研究[J]. 包装工程, 2005, 26(4): 54-55, 61.

[4] 贺挺挺. 电磁振动给料机的变频控制研究[D]. 沈阳: 沈阳理工大学, 2013: 3-5.

[5] 朱鹏飞, 黄松和, 冷东. 组合秤下料机构自适应控制[J]. 包装工程, 2015, 36(9): 90-94.

[6] 万文, 熊震江. 电磁振动给料机的 PID 控制[J]. 矿山机械, 2006, 34(5): 55-57.

[7] 赵庆荣. 电磁振动定量给料系统的设计与研究[D]. 沈阳: 东北大学, 2012: 63-66.

[8] 黄凤. 电磁振动给料机振幅的自适应控制[D]. 南京: 河海大学, 2007.

[9] 冯颖. 电磁振动式颗粒食品定量分装机的改进[J]. 食品与机械, 2016, 32(2): 84-87, 159.

[10] 苏俊明, 李振亮, 李亚, 等. 称重式包装机两级给料最优切换点的确定方法[J]. 食品与机械, 2015, 31(1): 99-103.

[11] 于雷. 电磁振动给料机特性分析和仿真控制[D]. 广西: 广西大学, 2008: 24-29.

[12] 顾平灿. 电磁振动给料器给料速度的研究[J]. 机电工程, 2012, 29(7): 790-794.

[13] 王述彦, 师宇, 冯忠绪. 基于模糊PID控制器的控制方法研究[J]. 机械科学与技术, 2011, 30(1): 166-172.

Electromagnetic vibration quantitative feeding system based on fuzzy PID

1QI Jun1

GONGDa-wei1

1LIYan1

2YANQing-qun2

(1.InstituteofAppliedTechnology,HefeiInstitutesofPhysicalScience,ChineseAcademyofSciences,Hefei,Anhui230031,China; 2.HefeiInstituteofTechnologyInnovation,ChineseAcademyofSciences,Hefei,Anhui230031,China)

To solve the problem of traditional electromagnetic quantitative feeding system in the process of the open loop control the feeding speed setting arbitrary large, not according to the intelligent control strategy for dynamic adjust the feeding speed, a quantitative electromagnetic vibration feeder was designed based on fuzzy PID control system. Taking the mechanical structure design of the system as a whole, the conduction angle of silicon controlled rectifier was obtained by theoretical analysis and mathematical relationship between amplitude, and according to this, the simplified mathematical model of electromagnetic vibration feeder second order was established. The simulation results show that the system has good dynamic, high control precision, high response speed and higher robustness, and also has good application prospect.

electro-vibrating feeder; fuzzy PID; the feeding speed

安徽省科技攻关项目(编号：1501041165)

戚俊(1971—)，男，中国科学院合肥物质科学研究院应用技术研究所研究员，博士。E-mail:jqi@aiofm.ac.cn

2016-10-04

10.13652/j.issn.1003-5788.2016.11.017