基于拉普拉斯金字塔的图像融合算法研究
2016-12-29余美晨孙玉秋王超长江大学信息与数学学院湖北荆州434023
余美晨,孙玉秋,王超 (长江大学信息与数学学院,湖北 荆州 434023)
基于拉普拉斯金字塔的图像融合算法研究
余美晨,孙玉秋,王超 (长江大学信息与数学学院,湖北 荆州 434023)
提出了一种改进的拉普拉斯金字塔图像融合方法。首先将源图像进行高斯金字塔分解,接着再进行拉普拉斯金字塔分解,然后对由拉普拉斯金字塔形成的图像序列的对应层分别使用不同的融合规则进行融合。顶层采用加权融合,其余层采用基于区域能量的融合规则进行融合,最后再进行拉普拉斯反变换得到重构图像。试验结果表明,该方法能够有效的保留图像信息,融合效果良好。
拉普拉斯金字塔;高斯金字塔;图像融合
图像融合所具有的改善图像质量、提高几何配准精度、克服目标提取与识别中图像数据的不完整性等优点,使得它成为当前重要的信息处理技术,并在遥感、医学、航天等领域得到广泛的应用。图像融合是指利用各种成像传感器获得不同图像,综合各图像的互补信息和冗余信息,产生一幅新的图像,以获得更为精确、可靠、全面的图像描述[1]。图像融合包括像素级融合、特征级融合和决策级融合[2]3个部分。近年来,人们提出了多种图像融合方法,其中像素级融合中的多分辨率图像融合方法较为常见,而拉普拉斯金字塔分解方法是多分辨率分析中的一类。基于拉普拉斯金字塔分解的图像融合算法的融合过程是将各个源图像分别在不同尺度、不同空间分辨率和不同分解层上分别进行的[3]。采用传统的拉普拉斯金字塔进行图像融合,最终得到的融合图像因细节丢失而变得模糊。为了能获得更好的融合效果, 保留更多的图像细节,笔者对传统的拉普拉斯金字塔图像进行了改进。
1 传统拉普拉斯金字塔图像融合
传统拉普拉斯金字塔图像融合的核心思想是通过构建分辨率逐层递减的金字塔,对各层金字塔按照一定的规则进行信息提取并利用上层信息逐层重构最终得到融合图像。 主要包括以下3个步骤:图像高斯金字塔形的建立、图像拉普拉斯金字塔形的建立和拉普拉斯金字塔反变换。把源图像分别用高斯低通滤波器进行低通滤波,接着再隔行隔列下采样,经过这个过程可形成一幅与源图像近似的子图像,再将该子图像插入一个适当的值使它膨胀,然后计算它与上一层图像的差值,得到带通分量。这个就是拉普拉斯金字塔的第1层,将这个近似图像重复做以上的分解过程,如此进行,可以得到其他层次,就构成了拉普拉斯金字塔。
1.1 图像的高斯金字塔分解
对源图像分别进行隔行降采样,接着隔列降采样,然后利用高斯窗口函数与得到的图像做卷积操作,就可以形成一列列的分辨率逐渐递减并且进行了低通滤波后的塔层。
设原始图像为G0,即塔层的第0层,对该层再进行低通滤波,接着间隔降采样,形成的图像记成G1,这就是高斯金字塔的第1层。重复进行上述操作过程,依次得到高斯金字塔的各层,即为G2,G3,…,GN。可以用函数GREDUCE表示每级之间的运算:
Gl=GREDUCE(Gl-1)
(1)
即对第l级图像上的点(i,j),0≤i≤Cl,0≤j≤Rl,1≤l≤N(N记为金字塔的总级数,G1、R1是作为金字塔第l级图像的高度和宽度)有:
(2)
式中,w(m,n)为高斯模板;w(m,n)=h(m)×h(n)为窗口函数;h取为高斯密度分布函数。
满足约束条件:
1)归一化性:
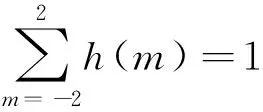
(3)
2)对称性:
h(i)=h(-i)
(4)
3)奇偶性:
h(0)+h(-2)+h(+2)=h(-1)+h(+1)
(5)
由以上条件可得:
(6)
窗口函数w(m,n)可表示如下:
(7)
至此,由G0,G1,…,GN构成了高斯金字塔[4],后面每层的大小都是它前面一个的4倍。
由上可知,REDUCE函数等同于用高斯模板对原始图像A、B分别作卷积运算,接着再对它们隔行隔列采样。然后定义一个函数EXPAND,它与REDUCE是互为逆运算。函数EXPAND是对高斯金字塔中每一层小的图像插入一个值,就把它的尺寸扩大成其前一个的尺寸。对Gl进行EXPAND运算后用Gl,k表示其结果,则:
Gl,0=Gl
(8)
Gl,k=EXPANDGl,k-1
(9)
(10)
1.2 图像的拉普拉斯金字塔分解
从金字塔底层图像重建上层未采样图像,即预测残差,把图像最大程度的还原。它所表现出来的是一组图像序列,记为L。即:
LN=GN
(11)
LN=Gl-EXPAND(Gl+1)=Gl-Gl+1,l0≤l≤N
(12)
式中,G0,G1,…,GN记为高斯金字塔;L0,L1,…,LN记为拉普拉斯金字塔。L0可以通过L0和L1执行一次EXPAND作相减而得到。
反复进行以上过程,得到一列列图像,该步骤即是拉普拉斯金字塔的构造过程。
1.3 拉普拉斯金字塔反变换
通过以上逆过程能重构G0。定义GN=LN,GN-1为GN执行一次EXPAND操作后和LN-1相加而来。依次类推,经过一系列上述过程,再作和运算,G0就依此来逆过程进行重构。
基于拉普拉斯塔形分解的图像融合的流程图如图1所示。
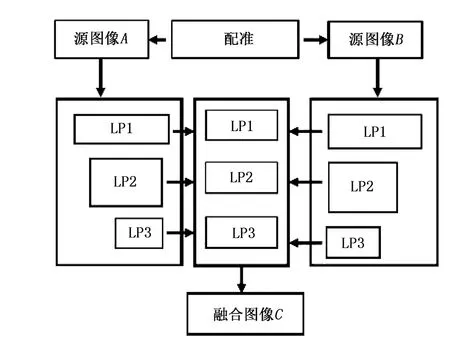
图1 拉普拉斯金字塔图像融合框图
2 改进的方法
源图像采用拉普拉斯金字塔的方法分解后,不同
的融合规则反映的融合结果不同,对融合效率的影响也不同。基于区域能量的融合规则考虑了周围像素的相互作用,可以很好的保留图像的细节和纹理信息。
基于区域能量规则的融合过程如下:
首先计算源图像对应局部区域的等效能量。选择局部区域的大小为3×3,加权系数为W(α,β),则拉普拉斯金字塔的第k层、以(i,j)为中心的局部区域能量Ek(i,j)为:
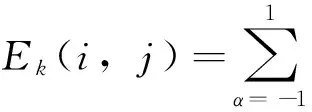
(13)
设待融合的2幅图像为A,B,融合后的图像为F,则计算局部区域的匹配度如下:
(14)
定义阈值e(0.5 若Mk,AB(i,j) (15) 若Mk,AB(i,j)≥e,则: (16) 其中加权融合算子的选择如下: (17) 3.1 试验结果 图像融合的关键技术包括图像特征点提取、图像匹配、图像融合3个方面。笔者在图像已配准的基础上用拉普拉斯金字塔图像融合方法融合2组图像:第1组是不同聚焦图像;第2组是普通摄影图像。试验仿真软件为Matlab 2012。 图2所示为左聚焦图像A1(背景清楚,闹钟模糊)和右聚焦图像B1(背景模糊,闹钟清楚)采用几种不同的方法进行融合的结果。图3所示为普通摄影的2幅源图像A2和B2(分别模糊了上部分和下部分)采用几种不同的方法进行融合的结果。 图2 不同聚焦的图像融合 图3 普通摄影图像融合 3.2 评价 通过试验结果可以看出,几种方法都有一定的融合效果,而且笔者提出的拉普拉斯法金字塔法融合效果较好[5]。但是由于人眼的感知能力不同,对图像的主观感受也有差别,因此还需要对图像的试验结果进行客观评价。 1)信息熵。 图像的信息熵是包含平均信息量多少的度量,其定义为: (18) 式中,p(i)为灰度i的分布概率,其范围是[0,1,…,L-1]。融合后图像的熵值大小反映了图像包含信息量的多少,熵值越大说明融合的效果相对越好[6]。 2)互信息。互信息smi也称为相关熵,是信息论的重要部分,可以用来衡量融合图像从源图像中继承信息的多少。原始图像A、B和融合后的图像F的互信息为: (19) 3)边缘保持度。边缘保持度的运算步骤如下: a)计算原图像IA、IB以及融合图像IF的梯度幅值和相角,以计算图像IA的梯度幅值和相角为例: (20) (21) b)计算IA与IF的相对幅值GAF(m,n)和相角AAF(m,n)以及IB与IF的相对幅值GBF(m,n)和相角ABF(m,n)。以计算前者为例: (22) (23) c)计算边缘幅值和相角保留程度: (24) (25) d)计算各像素边缘信息保留程度: (26) (27) e)最后得到边缘保持度客观评价指标: (28) 式中,M,N为图像长和宽;wA(n,m)=|gA(n,m)|L,wB(n,m)=|gB(n,m)|L(L为常数,笔者取1)。 不同聚焦以及普通摄影的图像融合结果客观评价如表1和表2所示,由表1、表2可知,拉普拉斯金字塔法要优于传统融合方法,能保留较多信息,效果较好。 表1 不同聚焦图像融合结果客观评价 表2 普通摄影图像融合结果客观评价 提出了一种基于拉普拉斯金字塔的图像融合算法,从试验结果可以看出,该方法对不同聚焦图像、普通摄影图像融合均取得了较好的效果,融合后的图像质量与一般方法相比有显著提升,具有一定的实用价值。 [1]何东健. 数字图像处理[M]. 第2版. 西安:西安电子科技大学出版社, 2008. [2] 朱瑞辉, 万敏, 范国滨. 基于金字塔变换的图像融合方法[J]. 计算机仿真, 2007, 24(12):178~192. [3] 陈浩, 王延杰. 基于拉普拉斯金字塔变换的图像融合算法研究[J]. 激光与红外, 2009, 4(4):439~442. [4] 席亮. 基于量子力学和拉普拉斯金字塔的图像融合方法[J]. 计算机与现代化, 2015, 12(4):37~41. [5] 于坤林, 谢志宇, 原振文. 改进的小波图像融合算法及应用研究[J]. 计算机与数字工程, 2014, 4(4):592~595. [6] 杜娟, 王少宇. 基于小波分解的多窗口图像融合[J]. 测绘信息与工程, 2007, 3(6):6~7. [编辑] 洪云飞 2016-09-16 国家自然科学基金项目(60572048);湖北省自然科学基金重点项目(2013CFA053)。 余美晨(1992-),女,硕士生,现主要从事数字图像处理方面的研究工作。 孙玉秋(1968-),女,博士,教授,博士生导师,现主要从事数字图像处理、模式识别等方面的教学与研究工作;E-mail: yqsun@yangtzeu.edu.cn。 TP391 A 1673-1409(2016)34-0021-06 [引著格式]余美晨,孙玉秋,王超.基于拉普拉斯金字塔的图像融合算法研究[J].长江大学学报(自科版),2016,13(34):21~26.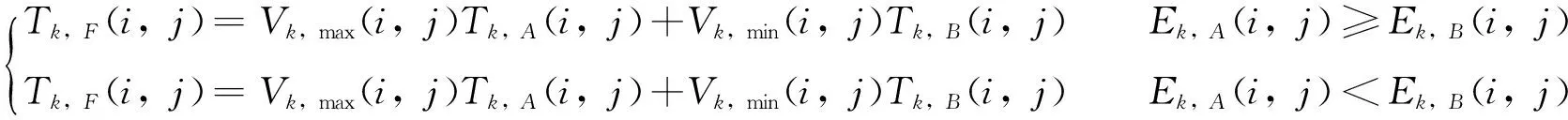
3 试验结果与分析评价


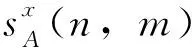
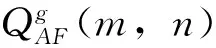


4 结语
