导向管底部泄流孔水力损失计算分析

徐建航， 杨翊仁

(西南交通大学力学与工程学院， 成都 610031)

导向管底部泄流孔水力损失计算分析

徐建航， 杨翊仁

(西南交通大学力学与工程学院， 成都 610031)

核燃料组件导向管底部泄流孔的水力损失系数对控制棒落棒时间和落棒速度有着重要影响。在落棒问题分析中，能否采用叠加理论计算泄流孔的水力损失，必须进行具体分析和论证。采用CFD方法对“突缩-突扩”型和“突缩-突缩”型两类四种泄流孔在不同流速下的水力损失进行了数值模拟计算，并与理论计算结果进行了对比。计算结果表明，对于流道内未充分发展的流动，理论计算结果与数值模拟计算结果存在一定差异。

泄流孔；落棒；未充分发展流动；水力损失；FLUENT

引 言

在反应堆安全分析中，紧急情况下的落棒时间是一个非常重要的参数。如图1所示，在控制棒下落过程中，导向管内部液体从导向管与控制棒间隙、上部泄流孔、底部泄流孔排出。液体从底部泄流孔排出的速度直接影响着控制棒的下落速度。获取不同流速下底部泄流孔的局部水力损失，进而计算导向管内部液体的排出速度，对于落棒时间分析非常重要。

图1 控制棒落棒示意图

导向管底部泄流孔是一个较为复杂的结构，国内学者在研究控制棒落棒运动时，多采用叠加理论计算底部泄流孔水力损失[1-3]。叠加理论的应用对象均是充分发展的流动，通过分段计算叠加求和的方法获得流道的水力损失。对于湍流而言，一般认为速度分布在大约20 D～40 D的长度内可以达到充分发展[4]。对于底部泄流孔而言，其各段流道长径比均较小，流道内的水流没有足够的空间进行充分发展。

另外，众多学者针对管路突扩水流流态也进行了广泛的研究，研究表明在管道截面突扩后部存在着回流、分离、重附和剪切等流动现象[5-7]，与充分发展水流流态存在较大差别。姚彦贵[8]等，针对反应堆一回路中突扩管内存在均匀孔板、突扩管与突缩管串联情况，利用Fluent进行了流阻计算分析，发现在圆管突扩后的未充分发展区域内放置阻力件时，采用叠加理论所得计算结果与数值模拟结果存在一定差异。因此，能否采用叠加理论计算泄流孔水力损失需要进行分析讨论。

本文采用CFD软件Fluent对导向管底部泄流孔的水力损失进行数值模拟，与叠加理论计算结果进行对比。探讨在落棒研究中采用叠加理论计算导向管底部泄流孔水力损失的可行性，并对比分析不同类型泄流孔的消能效果。

1 模型简述

本文在图1所示底部泄流孔基础上讨论两类截面突变泄流孔模型。一类是“突缩-突缩”型泄流孔，如图2所示，分两种计算工况，工况I的模型参数见表1，工况II的模型参数见表2。

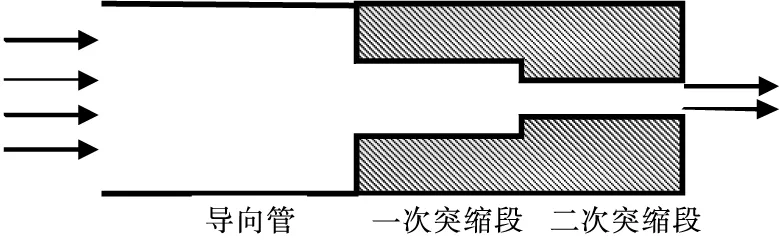
图2 “突缩-突缩”型泄流孔示意图

另一类是“突缩-突扩”型泄流孔，如图3所示，也分两种计算工况，工况III的模型参数见表3，工况IV的模型参数见表4。

计算所需其他基本参数见表5。

图3 “突缩-突扩”型泄流孔示意图

长度/m直径/m长径比导向管0.0300.0101052.97一次突缩段0.0270.00213.5二次突缩段0.0100.00110

表2 工况Ⅱ泄流孔模型参数

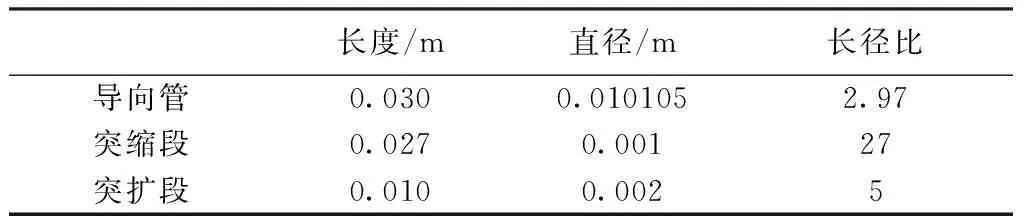
表3 工况Ⅲ泄流孔模型参数

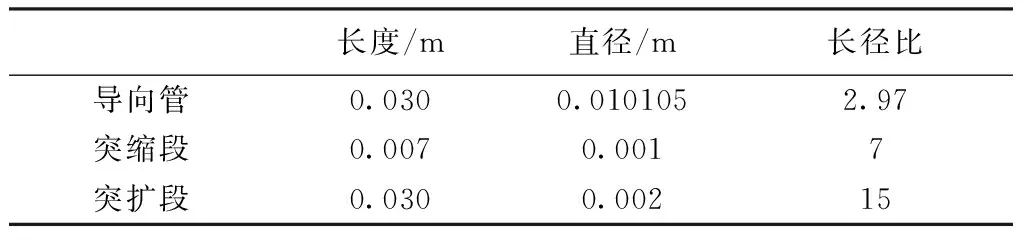
表4 工况Ⅳ泄流孔模型参数

表5 基本参数

2 计算方法

2.1 叠加理论计算方法

充分发展的圆管内流水力损失计算公式为：

hf=hl+hm

(1)

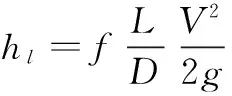
针对图2与图3所示模型，泄流孔水力损失叠加理论计算公式为：

hf=hl1+hl2+hl3+hm1+hm2

(2)

式中，hl1为导向管段沿程水力损失；hl2为中间段沿程水力损失；hl3为出口段沿程水力损失；hm1为水流由导向管段进入中间段局部水力损失；hm2为中间段进入出口段局部水力损失。

2.2 CFD计算方法

Fluent设置为3D模型，单精度，湍流模型采用Standard k-ε模型。壁面函数采用标准壁面函数，控制方程离散化先采用一阶迎风格式，在计算收敛后再采用二阶迎风格式提高计算精度。因为流体介质为水，可以忽略其压缩性，采用基于压力的求解器进行求解。

3 计算结果及分析

记水力损失理论计算结果为hft，数值模拟计算结果为hfc，数值模拟水力损失系数为ξc。数值模拟与理论计算结果相对误差为Ect=(hft-hfc)/hft×100%。

3.1 工况I泄流孔水力损失

工况I泄流孔为“突缩-突缩”型泄流孔。不同流速下的数值模拟和理论计算结果见表6。水力损失随流速变化曲线如图4所示。

由表6可知，工况Ⅰ泄流孔的水力损失数值模拟和理论计算结果吻合度偏低，相对误差绝对值在6.46%～15.06%之间。另外，由图4可知，随着入流速度的增加，工况Ⅰ泄流孔水力损失数值模拟结果与理论计算结果吻合度降低。

表6 工况I泄流孔水力损失计算结果

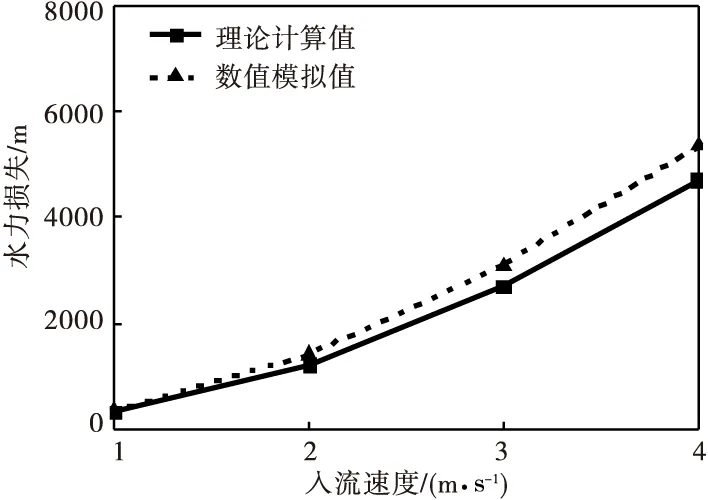
图4 工况Ⅰ水力损失随入流速度变化图

3.2 工况Ⅱ泄流孔水力损失

工况Ⅱ泄流孔也为“突缩-突缩”型泄流孔。不同流速下的数值模拟和理论计算结果见表7。水力损失随流速变化曲线如图5所示。

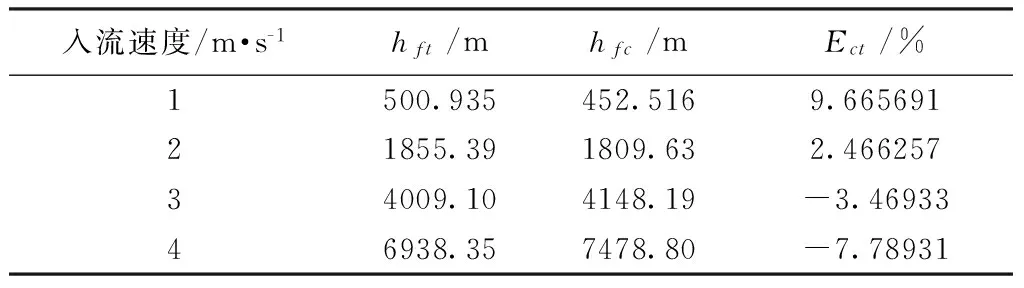
表7 工况Ⅱ泄流孔水力损失计算结果

图5 工况Ⅱ水力损失随入流速度变化图

由表7可知，对于工况Ⅱ泄流孔的水力损失，数值模拟和理论计算结果具有较高吻合度，相对误差绝对值在2.47%～9.67%之间。由图5可知，随着入流速度的增加，工况Ⅱ泄流孔水力损失数值模拟结果与理论计算结果吻合度降低。

3.3 工况Ⅲ泄流孔水力损失

工况Ⅲ泄流孔为“突缩-突扩”型泄流孔，不同流速下的数值模拟和理论计算结果见表8。水力损失随流速变化曲线如图6所示。

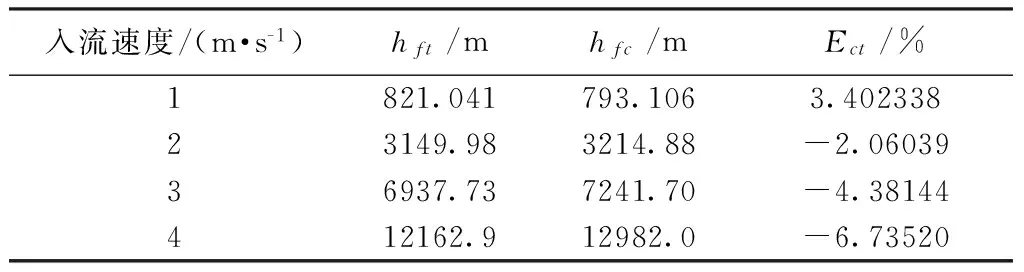
表8 工况Ⅲ泄流孔水力损失计算结果

图6 工况Ⅲ水力损失随入流速度变化图

由表8可知，对于工况Ⅲ泄流孔的水力损失，数值模拟和理论计算结果吻合度较高，相对误差绝对值在3.40%～6.74%之间。由图6可知：入流速度较低时，泄流孔数值模拟结果与理论计算结果吻合度较高，随着入流速度增加，吻合度降低。

3.4 工况Ⅳ泄流孔水力损失

工况Ⅳ泄流孔也为“突缩-突扩”型泄流孔。不同流速下的数值模拟和理论计算结果见表9，水力损失随流速变化曲线如图7所示。

表9 工况Ⅳ泄流孔水力损失计算结果

图7 工况Ⅳ水力损失随入流速度变化图

由表9可知，对于工况Ⅳ泄流孔的水力损失，数值模拟和理论计算结果吻合度很高，相对误差绝对值在0.08%～5.46%之间。由图7可知，随着入流速度的增加，工况Ⅳ泄流孔水力损失数值模拟结果与理论计算结果保持较高的吻合度。

3.5 消能效率对比

不同流速下4种工况水力损失系数见表10。

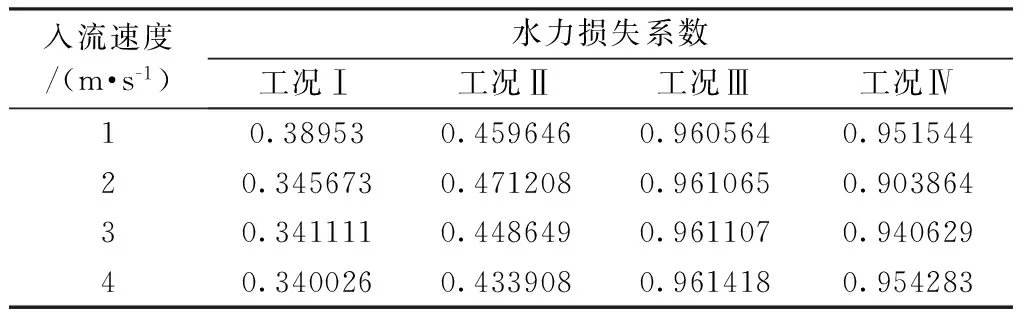
表10 不同流速下不同孔型水力损失系数

由表10可知，在相同入流速度下，“突缩-突扩”型泄流孔的水力损失系数要高于“突缩-突缩”型泄流孔，即“突缩-突扩”型泄流孔的消能效率更高。消能效率过高，则导向管内部液体排出速度慢，控制棒下落速度低，落棒时间过长。消能效率过低则会导致控制棒下落速度过快，引起控制棒碰撞破坏。因此在选择导向管底部泄流孔类型时，应综合考虑泄流孔类型对落棒时间和落棒速度的影响。

4 结 论

利用CFD软件FLUENT，对核燃料组件导向管底部泄流孔在不同孔型和不同入流速度下的水力损失进行了数值模拟计算，并与理论计算结果进行了对比。计算结果表明：

(1) 由于底部泄流孔各段流道“长径比”较小，流道内流动未充分发展，采用叠加理论计算底部泄流孔水力损失会存在偏差。

(2) 对于未充分发展流动的水力损失计算，叠加理论计算结果往往要低于数值模拟结果。除工况Ⅰ泄流孔外，对于本文所探讨的其他孔型，均是随着来流速度的增加，数值模拟计算结果与理论计算结果吻合度降低。

(3) “突缩-突扩”型泄流孔比“突缩-突缩”型泄流孔的消能效率高。

(4) 在落棒问题的流阻分析过程中，对于未充分发展流动的水力损失计算应做出详细的分析。对于具体问题，是否可以采用叠加理论计算水力损失，需要进行充分的分析和讨论，避免引起误差。

[1] 于建华,魏泳涛,孙磊,等.控制棒组件在流体环境中下落时所受阻力的计算[J].核动力工程,2001,22(3):236-241.

[2] 徐伟,刘彤,张炯,等.控制棒组件落棒时间分析[C]//中国力学学会反应堆结构力学专业委员会.第十七届全国反应堆结构力学会议论文集.上海:中国力学学会反应堆结构力学专业委员会,2012:5.

[3] 赵良举,彭云康,曾丹苓.秦山300 MW核反应堆控制棒热态落棒实验数值拟合[J].重庆大学学报:自然科学版,2000,23(6):107-109,120.

[4] 张明远.流体力学[M].北京:高等教育出版社,2010.

[5] KORNAKIED,LIAKOS HH,FOUNTI MA,et al.Numerical study of turbulent diesel flow in pipe with sudden expansion[J].Applied Mathematical Modelling,2001,25(4):319-333.

[6] FOUNTI.M,KLIPFEL A.Experimental and computational investigations of nearly dens two-phase sudden expansion flows[J].Experimental Thermal and Fluid Science,1998,17(1-2):27-36.

[7] 赵妍.应用FLUENT对管路细部流场的数值模拟[D].大连:大连理工大学,2004.

[8] 姚彦贵,施杨,张锴,等.一回路系统中冷却剂流动形阻分析[J].核动力工程,2015,36(5):83-86.

Hydraulic Loss Analysis of Bottom Drain Hole of Guide Tube

XUJianhang,YANGYiren

(School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Hydraulic loss coefficient of bottom drain hole of the guide tube of the nuclear fuel assemblyhas has important influence on the drop-time and the drop-speed of the control rod. In rod drop analysis, it is necessary to make a concrete analysis and demonstrate whether the hydraulic loss of the drain hole can be calculated by the classical superposition theory. The hydraulic losses of “sudden contraction-sudden expansion” and “sudden contraction-sudden contraction” two types, four kinds of drain holeat different flow velocities were calculated by CFD method, the results of which were compared with those of the theoretical calculation. The calculation results show that there are some differences between theoretical calculation and numerical simulation results.

drain hole; rod drop; un-fully developedflow; hydraulic loss; FLUENT

2016-03-21

国家自然科学基金项目(11372258)

徐建航(1992-),男,山东日照人,博士生,主要从事流固耦合动力学方面的研究,(E-mail)1689629924@qq.com; 杨翊仁(1959-),男,江西东乡人,教授,博士生导师,主要从事流固耦合动力学方面的研究,(E-mail)yangyiren05@126.com

1673-1549(2016)06-0044-04

10.11863/j.suse.2016.06.09

TB115

A