基于VB的测量坐标系统转换程序设计与实现

2016-12-28吕翠华张东明葛俊洁

地理空间信息 2016年12期

关键词：椭球直角坐标坐标系

吕翠华，张东明，葛俊洁

（1.昆明冶金高等专科学校测绘学院，云南昆明 650033）

基于VB的测量坐标系统转换程序设计与实现

吕翠华1，张东明1，葛俊洁1

（1.昆明冶金高等专科学校测绘学院，云南昆明 650033）

讨论了测量坐标系统转换中数学模型选择、参数计算、算法设计等几个关键问题，研究了利用VB语言编程实现测量坐标系统转换的方法，并通过实例进行了验证。

VB；测量；坐标系统转换；程序设计

过去的测绘成果资料的坐标系大多是1954年北京坐标系或1980西安坐标系，随着2000国家大地坐标系的推广，需要将这些测绘成果转换为2000国家大地坐标系。另外，为便于测绘成果的利用和管理，各种工程建设中常常涉及地方独立坐标系与国家坐标系的相互转换。因此，开发坐标系统转换程序，实现不同参考椭球基准下各种坐标系统之间的相互转换，是实际测量工作中急需解决的问题。

1 转换数学模型的选取

常用的坐标转换有平面四参数转换和七参数转换。平面四参数转换属于二维坐标转换，对于大地坐标，需通过高斯投影得到平面坐标，再计算转换参数。七参数转换有布尔莎（Bursa）模型、莫洛金斯基（Molodensky）模型、武测模型等，属于三维坐标转换。布尔莎模型是以原坐标系原点为中心，对坐标进行旋转、缩放和平移变换；莫洛金斯基模型是在测区范围选择一参考点作为变换中心，对坐标进行旋转和缩放，以原坐标系原点为中心进行平移变换；武测模型是以原坐标系原点为中心，对坐标进行旋转和平移变换，以测区某参考点为中心进行缩放变换[1]。

1.1 布尔莎（Bursa）模型

模型中共采用了7个参数，分别是3个平移参数ΔX、ΔY、ΔZ；3个旋转参数（也称为3个欧拉角）εX、εY、εZ和1个尺度参数μ。考虑坐标系统转换中旋转角均为极小角度，给出简化模型如下：

1.2 莫洛金斯基（Molodensky）模型

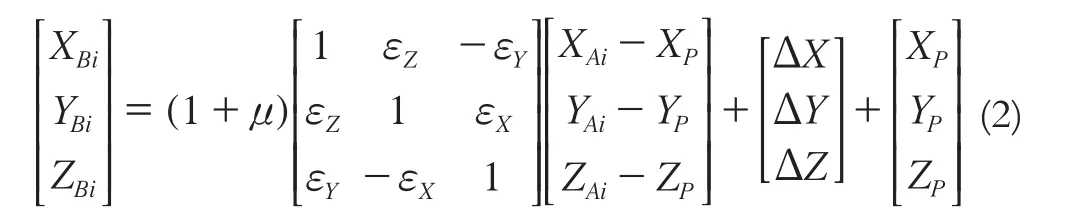
1.3 平面四参数转换模型

式中，ΔX、ΔY为平移参数；α为旋转参数，μ为尺度参数。

1.4 转换模型的选择

平面四参数转换只适用于小区域、不同定义下的两种坐标系转换，是工程应用较多的一种简单、直观且容易掌握的数学模型。七参数转换从理论上来说更加严密，它充分考虑了两套坐标系的椭球定位定向差异，保证了两套坐标系相对严密的转换，更适用于大型项目中的坐标转换。在实际应用中，要综合考虑待转换的两个坐标系的基本信息、转换区域距中央子午线的距离、区域大小、公共点的多少与分布等情况，以此来选择适宜的坐标转换模型[2]。

2 坐标系统转换的几个关键问题

测量坐标系统转换包括：相同参考椭球基准下平面直角坐标、大地坐标与空间直角坐标的相互转换，不同参考椭球基准下平面直角坐标、大地坐标与空间直角坐标的相互转换。各种坐标系统之间相互转换存在几个关键问题：①转换参数的求解；②高斯投影反算中底点纬度的解算；③由空间直角坐标反解大地纬度。

2.1 转换参数的求解

根据数学模型，求取三维坐标转换中的7个转换参数，至少需要3个公共点；求取二维坐标转换中的4个转换参数，至少需要2个公共点。通常，为减小转换误差，参与求解参数的公共点数量要多于最少公共点数，按最小二乘原理,由误差方程列出法方程，通过严密平差，解算出转换参数的最或然值[3]。

对于布尔莎模型，列出误差方程如下：

对于莫洛金斯基模型，将旋转缩放中心P（XP，YP，Zp）的坐标取值为公共点坐标平均值：

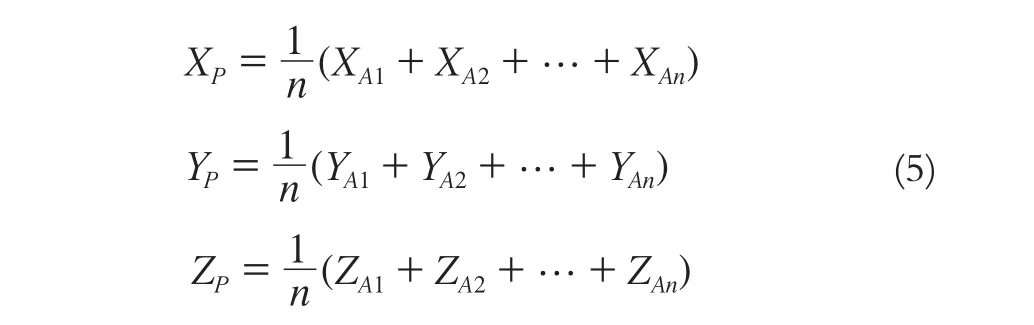
列出误差方程如下：

对于平面四参数模型，令a=（1+μ）cosθ，b=（1+μ）sinθ，列出误差方程如下：

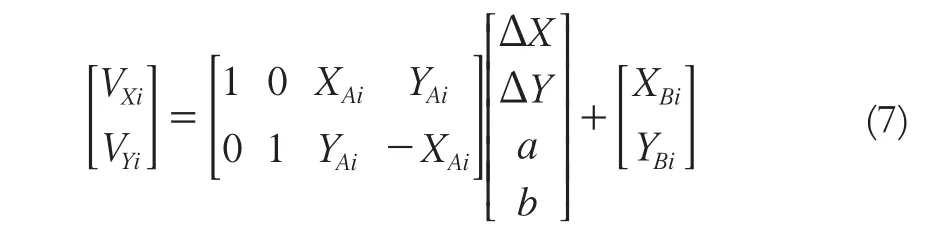
以上误差方程均可表示为V=Bx＇-l，将所有同名公共点视为等精度等权，根据最小二乘原理得：

从转换数学模型可知，在选择了参与求解转换参数的公共点后，坐标转换过程的实质就是根据公共点数量，动态组成B矩阵和l矩阵，且随着参与求解转换参数的公共点数量增加，矩阵也在不断增大。通过矩阵转置、相乘、求逆等一系列运算，求得转换参数。在程序设计中，只需将矩阵转置、相乘、求逆运算编写为独立的子程序过程，根据运算需要实时调用即可。

2.2 底点纬度的解算

求解底点纬度有很多算法，可归纳为迭代法、直接解法、数值解法等，这些算法虽思路不同，但计算效果等价[4]。结合计算机运算速度快、适合做重复性操作的特点，作者采用迭代法来求解。迭代法求解，需要确定4个关键点：迭代变量、迭代变量初始值、迭代关系式、迭代结束条件。这里设定迭代变量为底点纬度Bf，迭代变量的初值为：迭代公式为：

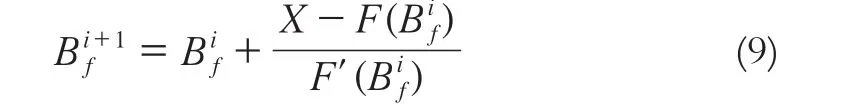
2.3 由空间直角坐标反解大地纬度

由空间直角坐标反解大地纬度相对较复杂。目前国内大地测量学者提出很多不同的解法，归纳为3类：一是直接解法，二是迭代解法，三是数值导数法[5]。采用迭代法来求解大地纬度B的方法如下：

选择迭代变量为tanB，设定迭代变量的初值为：

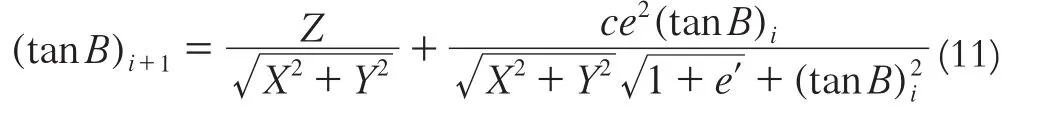
3 程序设计与实现

3.1 功能设计

VB6．0具有简单易用、快捷方便的特点，与Excel等办公软件有很好的接口，适合开发非底层计算机应用软件，故选择VB6．0作为开发工具。程序主要功能设计为：

1）同一椭球基准下的坐标系统转换。包括大地坐标与空间直角坐标的互换，大地坐标与高斯平面坐标的互换，高斯平面坐标与空间直角坐标的互换。

2）不同椭球基准下的坐标系统转换。提供3种转换模型：布尔莎模型、莫洛金斯基模型、平面四参数模型。

3）生成转换报告，对转换精度进行分析评价。

4）实用工具。包括坐标换带计算，空间距离计算、方位角计算等。

3.2 数据组织与结构设计

1）为便于数据导入和管理，批量输入输出的坐标数据采用通用的ASCⅡ码文本格式和Excel数据表格式进行组织。

2）程序设计中，对于经纬度坐标，约定输入格式为“度．分秒”。为方便程序调用，所有坐标数据均用一维数组来存储。

3）坐标系统转换涉及4种椭球：克拉索夫斯基椭球、1975国际椭球、WGS-84椭球和CGCS2000椭球。将不同椭球参数统一写入独立的子程序过程，约定不同的椭球基准编号，以椭球基准号为过程传递参数，通过判断椭球基准ID来调用相应的椭球参数。

4）在转换参数计算时，综合运用MSFlexGrid和Text控件，将公共点坐标数据输入界面设计为表格形式[6]，模拟电子表格输入、显示和编辑，使数据输入和编辑操作简单快捷，如图1所示。

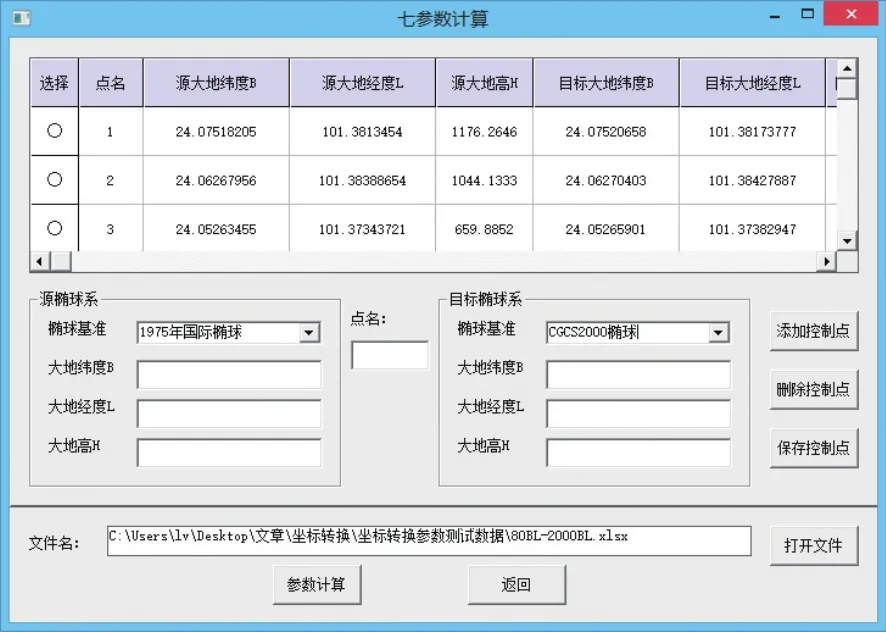
图1 七参数计算界面

3.3 转换流程

1）数据准备。需提供测区内具有2套坐标系（原坐标系和目标坐标系）的公共点坐标，选择一定数量的精度可靠、分布合理、覆盖整个测区的公共点参与转换参数计算。若是七参数转换，则提供经纬度和大地高；若是四参数转换，则提供平面直角坐标；以Excel表形式编辑保存。待进行坐标转换的数据以TXT文本文件编辑保存。

2）设置投影参数，包括中央子午线经度、Y坐标加常数、投影高程等。

3）设置原坐标系和目标坐标系，选择椭球基准，确定转换模型。

4）读取参与转换参数计算的公共点坐标，计算转换参数。

5）利用参与转换参数计算的公共点计算内符合精度，利用未参与转换参数计算的公共点计算外符合精度，查找并剔除用于计算坐标转换参数的粗差公共点[7]，用可靠公共点重新计算坐标转换参数，直到精度满足限差为止。

6）读取需要进行坐标转换的数据，根据转换参数，执行坐标转换，求解出所有待转换点的转换坐标。

4 实例验证

选取某矿区分布均匀、坐标精度可靠且覆盖整个矿区的5个公共点计算转换参数，选取8个未参与转换参数计算的公共点作为外部检核点，利用2015年的矿区大地水准面精化成果内插高程异常值，分别运用布尔莎模型、莫洛金斯基模型和平面四参数模型进行1954年北京坐标系到2000国家大地坐标系、1980西安坐标系到2000国家大地坐标系的转换。转换精度统计见表1。根据程序运行结果，分析得到：

1）由于1954年北京坐标系的大地点坐标是经过局部分区平差得到，而1980西安坐标系的大地点坐标是经过整体平差得到，故1954年北京坐标系统的内符合性较差，其相应坐标转换的内符合精度和外符合精度比1980西安坐标系低，程序运行结果证实了这一点。