LiDAR三维重建中基于CSG方法的扩展研究

査达剑, 李乐林, 江万寿, 韩用顺

(1.湖南科技大学地理空间信息技术国家地方联合工程实验室，湘潭 411201； 2.武汉大学测绘遥感信息工程国家重点实验室，武汉 430079)



LiDAR三维重建中基于CSG方法的扩展研究

査达剑1, 李乐林1, 江万寿2, 韩用顺1

(1.湖南科技大学地理空间信息技术国家地方联合工程实验室，湘潭 411201； 2.武汉大学测绘遥感信息工程国家重点实验室，武汉 430079)

针对机载激光雷达(airborne light detection and ranging，LiDAR)数据三维重建中运用构造表示法(constructive solid geometry,CSG)无法对复杂模型自动地进行基元分解、基元模型识别以及模型集成等问题，提出了一种基于CSG扩展的三维重建方法。该方法利用建筑物等高线的分族特性，通过等高线分族实现了CSG方法中复杂建筑物模型的层次划分和基元分解，在此基础上，结合建筑物分层等高线族特征和分层轮廓线的重建结果来辨别基元类型，实现了CSG方法中基元的自动识别，并依据其识别结果采用相应的重建方法完成模型基元的分部重建，最后依据一套有效的模型集成规则实现了复杂建筑物整体模型的自动建模。通过大范围的LiDAR数据进行试验，验证了基于CSG扩展方法对复杂建筑物三维建模的有效性。

LiDAR； 三维重建； CSG； 基元分解； 基元识别； 等高线族； 轮廓重建

0 引言

近年来，随着三维GIS技术的不断发展，三维数字城市正成为数字城市到智慧城市升级的主要建设内容之一[1]。目前城市三维数据获取手段主要还是基于摄影测量的方法，利用影像信息提取建筑物目标的几何特征信息。从本质上说，从二维影像恢复三维模型仍然是一个病态问题，虽然近年来密集匹配技术[2-3]的研究已取得了较大的进展，但随着传感器技术的发展，可获得的影像资料的空间分辨率、光谱分辨率不断提高，快速获取大范围复杂目标的高精度多细节层次的三维几何模型仍然是世界性难题[4]。具有直接获得地物目标三维信息的机载激光雷达(airborne light detection and ranging，LiDAR)技术的出现，为快速获取三维城市模型的提供了一种新的重要手段[5]。

三维重建之前，一般都会确定该重建方法采用何种模型来描述建筑物。目前主要的建筑物模型可以分为通用模型和参数模型2大类，其中通用模型又可细分为棱柱体模型、体系构造表示模型(constructive solid geometry models，CSG)和多面体模型。一旦确定了三维重建的几何模型，便可根据模型的类别采用相应的重建方法。目前基于LiDAR数据的模型重建方法可以分为模型驱动[5-8]、数据驱动[9-12]和混合驱动[13]3大类方法。棱柱体模型和CSG模型适用于模型驱动的方法，而多面体模型则更适合于数据驱动的三维重建方法。模型驱动的方法采用自上而下的重建策略，需要事先建立包含各种基本模型的模型库，如平顶型、人字型、书桌型、四坡型等，重建时基于模型库中已有的模型基元采用贝叶斯推理或可逆跳转马尔科夫链蒙特卡罗算法(reversible jump Markov chain monte carlo,RJMCMC)等方法[6,7]进行模型匹配，确定出模型的各个参数值。由于在建立模型基元时已经隐含了诸如平行、垂直条件等拓扑约束关系，重建模型的规则化程度很高，甚至在局部因遮挡等原因出现数据缺失情况下也能很好地完成重建任务[5,8]。普通的平顶、人字顶等房屋，采用柱体模型或参数模型即可有效地完成重建任务，但对于复杂的建筑物，由于单个模型基元的描叙能力有限，通常需要采用构建CSG模型的方法，将简单的模型基元进行一系列的布尔运算来组合表达最终的建筑物模型。与模型驱动方法相反，数据驱动的方法则采用自下而上的重建策略，通过采取诸如三维霍夫变换(3 dimensional hough transform,3DHough)[9]、区域增长[10]、二叉空间分割树(binary space partioning tree,BSP)[11]、全局优化[12]等分割方法对点云数据进行分割，提取面片并通过面片求交得到房屋角点、屋脊线等特征，同时建立各个面片间的拓扑关系，采用多面体模型以边界线表示法(boundary representation，B-Rep)来描述建筑物。其重建结果不受模型库中已有模型种类的限制，可以重建一些比较复杂的模型。理论上数据驱动的方法可以重建任意形状的房屋，但是由于测量数据中往往存在着各种随机噪声，重建结果容易产生偏差，算法的鲁棒性不如模型驱动的方法，但其灵活性则要高于模型驱动的方法。混合驱动的方法则结合模型驱动和数据驱动，以数据驱动的方法提取基元，并通过模型库中的模型基元进行验证与精化[13]。对于具有多层次复杂结构的建筑物，三维重建不仅要恢复单个屋顶各个面片的高度、形状、位置、方向等几何参数以及面片间的拓扑关系，还需要从体模型的角度考虑恢复出各层模型间的拓扑关系。CSG模型是一种实体构建模型，被计算机辅助设计界广泛采用[14-15]，但其模型构建过程中需要人为地选择模型基元通过一些预设的参数和布尔等操作来构建他们所要的建筑物模型。对于LiDAR数据三维重建这种逆向工程问题，CSG模型显得不太合适，其主要原因在于布尔操作的歧义性和CSG模型树的构建问题。对于一个复杂的建筑物可以通过多种方法来组合模型基元达到所要的结果，比如对于一个简单的L型房屋，由于基元的参数和相对位置不确定，如果通过自有组合，仅采用联合操作就有4种等效的方案[8]。为此，笔者认为若要采用CSG模型须对其在以下几个方面进行扩展方可适应LiDAR数据的三维重建：

1)模型库的完备性问题。为了重建各种复杂建筑物，模型基元必须尽可能地囊括所有模型类别，否则重建可能失效。

2)建筑物的基元分解问题。利用地面规划图等GIS数据在一定程度上可以辅助进行分解，但在缺少此类辅助数据的情况下如何将复杂建筑物轮廓进行有效的分解，使得重建结果与实际的建筑物形状相吻合。

3)模型基元的选择问题。计算机自动模型选择中虽然采用穷尽枚举的最小二乘拟合方法能够实现重建的目的，但是在大场景数据的三维重建前提下，对各个基元进行遍历，其重建效率自然低下，智能化的模型选择方法还需做进一步研究。针对CSG方法在应用到LiDAR点云的三维重建过程中无法实现建筑物模型基元的自动分解、识别以及合并问题，笔者在这几个方面对CSG方法进行相关的扩展研究，以期使得CSG方法可以实现对LiDAR点云中具有多层次、多样式屋顶的复杂建筑物三维模型进行有效、精细的自动重建。

1 CSG方法扩展

本文对CSG方法的扩展主要从CSG方法中的基元分解问题、基元模型组件树的构建问题、CSG方法中的基元识别问题和CSG方法中的基元合并问题4个方面展开。

图1所示为本文的基于CSG扩展的建筑物三维重建思路。建筑物三维模型重建过程中主要根据建筑物等高线的分族特征及等高线规则化后的线型特征进行自动分解、识别和合并。该方法对CSG方法的扩展主要体现在以下几个方面： ①通过等高线族分析，将建筑物等高线分为不同层的等高线族实现基元分解； ②通过对各个等高线族的形状特征进行分析实现基元识别，并依据识别结果选择不同的重建方法进行重建，得到不同层的分部模型； ③依据等高线族之间的拓扑关系恢复模型间的联系，并通过一些约束条件和平差方法将基元模型进行聚合而得到整体模型。

图1 基于CSG扩展的三维重建思路

该重建方法基于传统的CSG模型构建方法，但又有不同之处，主要表现在以下2点：

1)CSG方法需要预先定义一些粒度较细的模型基元组成基本模型库，重建时从模型库中选择模型基元，通过交、并等布尔运算进行模型组合。本文方法则不需要强调模型的粒度问题，模型分割后可以通过实际建筑物各组成部分的类型灵活地采用参数模型、棱柱体模型、多面体模型等进行重建。以一个具有多个垂直转角的平顶屋为例，CSG方法需要对该模型进行多次的分割才能完成重建任务，而基于等高线族分析的方法则只需要通过单族等高线分析，获得其外围轮廓并以棱柱体模型来表示。

2)CSG方法中整体模型的分割过程主要通过人工操作来完成，自动化程度不高，而且其模型组件树的衍生过程相对复杂，不易操作。本文方法对建筑物的分割是通过对建筑物等高线族的分族过程自动完成，且各族之间拓扑关系十分明确，有利于后期进行分部模型的集成。

图2为本文提出的CSG扩展方法的三维重建流程图。该流程中主要包括基元分解、基元识别、基元重建及基元合并4个阶段。在前期研究中[16]，笔者对建筑物等高线进行分族分析，实现了复杂建筑物的层次划分和基元分解，同时依据等高线族的拓扑关系构建等高线族树实现了模型组件树的自动构建。需要说明的是，由于基元重建主要依赖基元的类型识别，根据基元模型类型分别采用已有的重建方法进行，这部分工作不是本文将要讨论的重点内容。而本文主要着重于基元识别和基元合并这2个方面的研究。

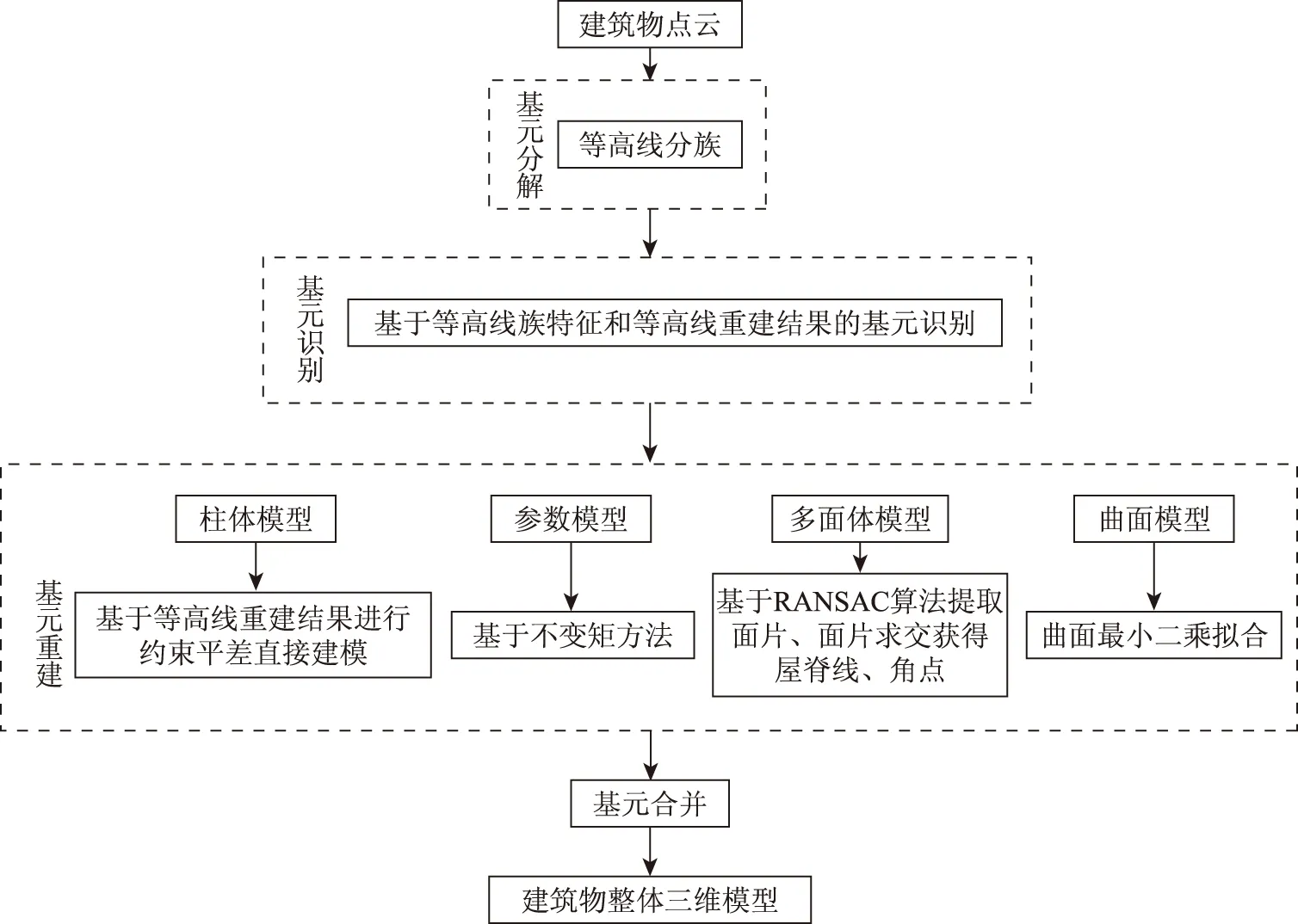
图2 基于CSG扩展的三维重建基本流程

可以看到，本文方法不但能够有效地使用各种不同类型的模型来进行三维重建，还可以根据模型类型的不同选择模型驱动或数据驱动的建模方法来进行三维建模，较单一的重建方法更具伸缩性。另外，本文提出的基于CSG扩展方法能够通过对等高线的形状分析来判断曲面屋顶的存在与否，这是基于点法向量分析或面片提取的重建方法所不能做到的，这也丰富了建筑物屋顶的表现形式。

2 基元识别

2.1 基元的等高线族特征

由于LiDAR系统提供的数据为离散的三维点云信息，缺乏模型的整体形状信息和轮廓信息，因此，直接从三维点云中进行模型类型的判断有一定的难度。建筑物等高线是在不同高程面上对建筑物进行水平切割后获得的高程切片的外部轮廓线。等高线的优势在于首先它是封闭的，能够提供建筑物的轮廓信息或形状信息，利用等高线的轮廓形状以及同一等高线族中等高线间的变化趋势可推测出建筑物模型的类型。

通过对几种基本模型的等高线族特征做进一步的研究，概括如表1所示。表1中的λx和λy为等高线间通过形状匹配后得到的坐标相似变换参数[16]。

表1 几种基本模型的等高线族特征

2.2 基元轮廓重建

等高线分族实现了基元的分解，每个等高线族中高程最低的那根等高线便为该基元的外围轮廓线。现实世界中，大部分房屋都是由规则的多边形组成，有很多对边是平行的，而且大部分的相邻墙面都是直角相交的，因此还需要对该等高线进行规则化。由于LiDAR数据生成的等高线多带有锯齿形的噪声，通常的多边形规则化方法不能保证等高线特征角点的提取。为此，本文提出了一种基于极化角点指数的多边形近似方法[17]来获得基元轮廓的初始角点。多边形近似的方法对于一些只有直线边构成的轮廓线来说已经完成了曲线轮廓的重建，但有些轮廓线中含有部分弧线段或是全部由弧线组成，而且对于轮廓线中是否含有弧线段是本文对基元进行模型识别的一个重要依据，因此，等高线经过多边形近似检测出特征角点后还需对其中的弧段进行识别。

本文的直、曲混合的数字曲线重建流程如下：

1)轮廓曲线点序调整。若多边形近似检测发现，轮廓线的起点不是特征角点，则按照原始轮廓线上点的排列顺序重新调整点的排列顺序： 第一个特征点之前的点按序依次放到原始轮廓线最后一个点之后，第一个特征点之后的点仍然保持与第一个特征点的相对顺序，确保轮廓线上第一个点为特征点； 若轮廓线上第一点为特征点，则保持原有点的排序。

2)根据最小二乘原理，用曲线上的所有点进行圆弧拟合并计算出拟合残差标准差б。

3)若拟合残差标准差б小于阈值Tv，则判定该条等高线为圆弧形，根据拟合的结果调整等高线上点的坐标位置； 若б大于Tv，则比较所有特征点的拟合残差v，将曲线在拟合残差最大的特征点处分割为2条曲线。

4)对新的曲线段重复执行步骤2)—4)，直到没有新的曲线段可以分割为止。

图3所示为对一含有弧段的建筑物等高线进行多边形近似及曲线识别的结果。从图3(b)中拟合出的紫色圆弧来看，本文方法能够正确地识别出直曲混合曲线中的弧段部分，一方面有利于获得更加精细的建筑物轮廓，另一方面可为含有曲面的基元进行类型识别提供依据。

(a) 多边形近似结果 (b) 多边形近似后曲线弧段识别结果

图3 轮廓线多边形近似及曲线识别结果

Fig.3 Polygonal approximation of contour and recognition result for curve

2.3 基元识别流程

本文的模型基元识别主要依据等高线分族特征及二维轮廓重建后的线型来进行。首先依据等高线分族中相似变换参数λx和λy来判断该基元是柱体模型还是斜面体模型，然后再根据二维轮廓重建结果做进一步的判断其具体的模型类型。若基元为柱体模型，则该族内的等高线基本上相同，λx和λy均趋近于1.0； 若柱体模型中包含曲面墙面，则二维轮廓重建结果中必包含曲线； 若基元为斜面体模型，则该族内的等高线只能相似，且相似变换参数λx和λy视模型类型的不同其取值均有所不同； 若基元为曲面顶模型，则族内等高线相似且二维轮廓重建后其线型比为曲线。综合等高线族特征及二维轮廓重建结果，本文的基元类型识别流程如图4所示。

图4 基元识别流程

3 基元合并

由于基元在重建阶段只是依据本族的等高线进行的，没有考虑其上下族的等高线位置和形状，这有可能导致模型基元间存在轮廓线位置、角点位置不一致性问题。因此当基元重建完毕，将这些独立的模型整体集成时需要考虑模型轮廓的一致性和整体性，需要制定一些规则来指导基元模型的合并过程(图5)。

(a) 线段间平行 (b) 线段间平面位置一致(c) 线段间平面位置一致

一致性约束性约束(长度差异较大)性约束(长度相等)

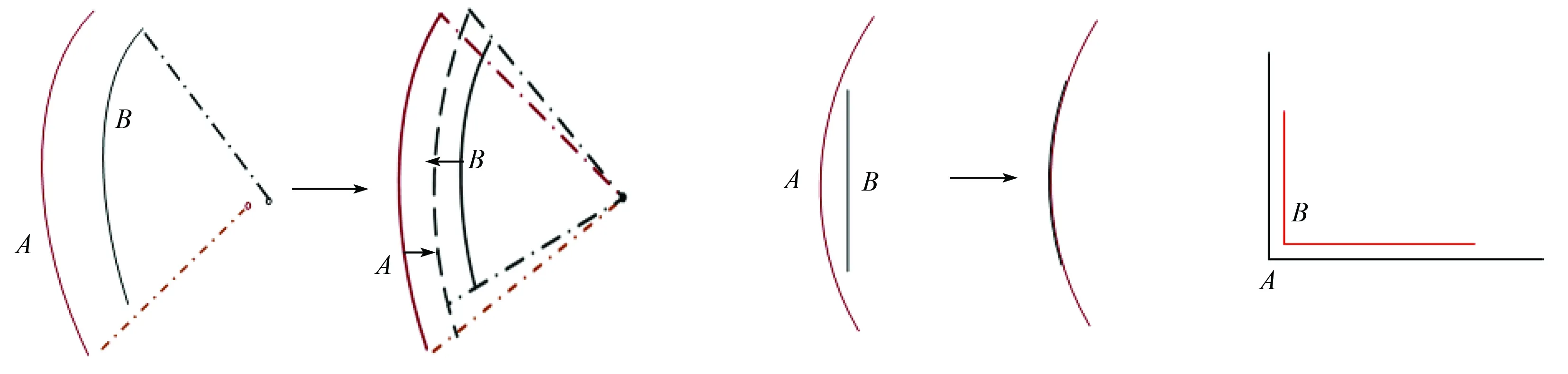
(d) 弧段间平面位置一致性约束 (e) 曲线、直线平面位置一致性约束 (f) 角点平面位置一致性约束

图5 基元模型合并规则示意图

Fig.5 Combination rules for the model primitives

笔者给出以下几条合并规则来约束基元模型的合并：

1)线段间平行一致性约束。如图5 (a)所示，若上下层模型轮廓线A、B距离很近，且二者的夹角很小时，则认为线段A与线段B为平行关系。调整时依据线段长度来判断，长度较长的那条线段作为调整基准。如图所示，以短线段B的中点为旋转基准，将B的斜率进行调整，使其与A平行。

2)线段间平面位置一致性约束。若上下层模型两线段平行且距离很近时，看其是否有重叠部分，若没有则均保留； 若有重叠部分且长度差异太大时，将短线段调整为与长线段一致(图5 (b))； 若两者长度相当，则取其平均(图5 (c))。

3)弧段平面位置一致性约束。若上下层模型2弧段距离很近，且半径相差不大、圆心距离不远时，取平均方式为将两弧的半径平均，作为新的半径，以两圆心的中点作为取平均后的圆弧的圆心，首尾端点取原本2弧所能形成的最长弧，作为新的圆弧端点(图5 (d))。

4)曲线、直线一致性约束。若上下层模型有一弧段和一直线段距离很近，且弧段长度远超直线段，则将直线段调整为曲线段，过圆心与直线段端点向弧段做径向射线，所得交点即为调整弧段的新端点(图5 (e))。

5)角点平面位置一致性约束。如图5 (f)所示，若上下层模型的角点A与角点B彼此距离很近，则通常认为这2个角点的平面位置应该是同一位置； 若2角点的平面位置距离超过阈值则认为这2个角点为非同一角点。位置调整的原则依据连接这2个角点的线段的长度来判断，选择连接线段最长的那个角点平面位置作为最终角点的平面位置。连接线段越长，说明该角点的位置越稳定。大多数情况下，角点位置一致性调整并不是孤立完成的，通过以上几条一致性规则判断，大部分的模型角点位置将符合一致性要求。

4 实验结果及分析

为了测试本文提出的基于CSG扩展的建筑物三维模型重建方案的可行性，选定多伦多(Toronto)某地区一组机载LiDAR数据进行试验。该区域覆盖范围600 m×750 m，高程范围45.6～184.0 m，平均激光点间距为0.8 m。图6所示为该区域LiDAR点云平面图。该区域内建筑物大多为具有多层次复杂结构的建筑物，仅有个别建筑物为单层矩形结构，且在数据中下部处有一栋两侧为弧形墙面平顶塔楼、中部为曲面屋顶的联合建筑物体(图6(a)中黑色线框区域)。该建筑为多伦多市政大厅所在。图6(b)为该区域点云基于CSG扩展方法得到的建筑物三维模型。为了说明具体的重建步骤，选定市政大厅做详细说明。

(a) 点云平面投影 (b) 三维重建效果图

图6 多伦多地区某区域三维重建结果

Fig.6 3D Reconstruction results for sectional region of Toronto

图7为多伦多市政大厅三维重建过程及结果。图7(a) 为市政大厅的原始等高线平面投影。图7(b)为该栋建筑等高线通过分族分析后获得的等高线族，通过分族该建筑物等高线被分成了左右塔楼、中央屋顶、底部基座及右侧屋顶的附属部件5个部分，可以看出等高线分族实现了该复杂建筑物的基元分解。图7(c)为通过等高线族进行基元识别后获得的基元轮廓,由于中间屋顶基元识别结果为球面屋顶，因此仍保留规则化后的等高线予以显示; 从图7(c)可以看出基元间有多处轮廓存在不一致的现象发生。图7(d)为基元模型轮廓经过一致性约束后的调整结果，从图7(c)中圈选区的部分轮廓线段与图7(d)相应部分对比可以发现， 上下层模型间的轮廓达到了一致性要求。图7(e)为经过一致性调整后获得的模型轮廓线与原始等高线套合图，从套合结果可以看出，模型最终轮廓整体达到要求。图7(f)则为获得的该栋建筑物最终整体三维模型。

(a) 原始等高线平面图 (b) 等高线族(c) 基元初始轮廓线平面投影

(d) 基元轮廓线一致性调整结果(e) 基元轮廓线套合原始等高线(f) 建筑物最终三维模型

图7 多伦多市政大厅三维重建过程及结果

Fig.7 Process of 3D reconstruction and result for Toronto city hall

5 结论

本文针对LiDAR数据三维重建中运用CSG方法无法有效地实现复杂建筑物三维模型自动精细重建的不足，提出了一种基于CSG扩展的三维重建方法。该方法通过对建筑物等高线进行分族、特征提取、轮廓重建等系列处理，解决了原有CSG方法在应用到LiDAR数据三维重建中对复杂建筑物模型无法自动地进行基元分解、基元模型识别等问题。本文的扩展研究实现了CSG方法中复杂建筑物模型的基元分解与识别，提出了一套有效的模型集成规则，实现了复杂建筑物整体模型的自动建模。基于大范围机载LiDAR数据所进行的试验表明，本文提出的CSG扩展三维重建方法是有效的。与现有的其他三维模型重建方法相比，本文方法不但可以实现多层次复杂建筑物基元模型层次结构间拓扑关系的有效重构，还可以很方便地将建筑物模型类型的三维识别问题转化为二维的平面识别问题，大大减小了模型识别的难度。同时，利用该方法不但可以重建平面屋顶，还可以解决其它方法难以对曲面屋顶进行识别、重建的问题。此外，该方法还可以根据建筑物模型的复杂程度自动集成多种重建方法来进行合理的重建，其模型选择的灵活性和实用性较强，使得建筑物三维重建可以不拘泥于某一单独的重建方法，有效地提高了现代三维城市模型的构建的自动化程度和三维模型的细节水平。

本文方法目前的不足之处在于该方法是建立在对等高线进行分析基础之上进行的，因此其三维模型重建的效果在一定程度上依赖于前期从LiDAR点云中提取的建筑物等高线与真实建筑物形状的吻合程度。如果在城市的LiDAR点云中进行三维重建，获取的等高线一般都会满足该要求。但若将该方法应用到城镇建筑物三维模型重建过程中，由于部分老旧的建筑物周围通常都会有很多高大树木与其毗邻，由此得到建筑物等高线与树木等高线混杂的情况时有发生，因而无法有效地将等高线中树木部分去除，最终影响到了整体模型的真实程度。下一步的工作将主要解决该方法在应用到植被覆盖度较高的城镇环境中如何有效地将建筑物等高线和植被等高线进行分离的问题。

[1] 朱庆.三维GIS技术进展[J].地理信息世界,2011,9(2):25-27,33. Zhu Q.Technical progress of three dimensional GIS[J].Geomatics World,2011,9(2):25-27,33.

[2] Yang Q X.A non-local cost aggregation method for stereo matching[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Providence,RI,USA:IEEE,2012:1402-1409.

[3] Zhang K,Fang Y Q,Min D B,et al.Cross-scale cost aggregation for stereo matching[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition.Columbus,Ohio:IEEE,2014:1590-1597.

[4] 朱庆.三维GIS及其在智慧城市中的应用[J].地球信息科学学报,2014,16(2):151-157. Zhu Q.Full three-dimensional GIS and its key roles in smart city[J].Journal of Geo-information Science,2014,16(2):151-157.

[5] Elberink S O,Vosselman G.Building reconstruction by target based graph matching on incomplete laser data:Analysis and limitations[J].Sensors,2009,9(8):6101-6118.

[6] Lafarge F,Descombes X,Zerubia J,et al.Structural approach for building reconstruction from a single DSM[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(1):135-147.

[7] Huang H,Brenner C,Sester M.A generative statistical approach to automatic 3D building roof reconstruction from laser scanning data[J].ISPRS Journal of Photogrammetry and Remote Sensing,2013,79:29-43.

[8] Xiong B,Elberink S O,Vosselman G.A graph edit dictionary for correcting errors in roof topology graphs reconstructed from point clouds[J].ISPRS Journal of Photogrammetry and Remote Sensing,2014,93:227-242.

[9] Sohn G,Huang X F,Tao V.Using a binary space partitioning tree for reconstructing polyhedral building models from airborne LiDAR data[J].Photogrammetric Engineering & Remote Sensing,2008,74(11):1425-1438.

[10]Zhou Q Y,Neumann U.2009.A streaming framework for seamless building reconstruction from large-scale aerial LiDAR data[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Washington,DC:IEEE,2009:2759-2766.

[11]Sampath A,Shan J.Segmentation and reconstruction of polyhedral building roofs from aerial LiDAR point clouds[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(3):1554-1567.

[12]Yan J X,Shan J,Jiang W S.A global optimization approach to roof segmentation from airborne LiDAR point clouds[J].ISPRS Journal of Photogrammetry and Remote Sensing,2014,94:183-193.

[13]Rottensteiner F.Consistent estimation of building parameters considering geometric regularities by soft constraints[C]//International Archives of Photogrammetry,Remote Sensing and Spatial Information Sciences.Bonn,Germany:IRPRS,2006,36:13-18.

[14]Wang C C L,Leung Y S,Chen Y.Solid modeling of polyhedral objects by layered depth-normal images on the GPU[J].Computer-Aided Design,2010,42(6):535-544.

[15]Bénière R,Subsol G,Gesquière G,et al.A comprehensive process of reverse engineering from 3D meshes to CAD models[J].Computer-Aided Design,2013,45(11):1382-1393.

[16]李乐林,江万寿.基于等高线族分析的LiDAR点云建筑物模型自动识别及重建[J].测绘通报,2013(10):23-25,29. Li L L,Jiang W S.Automatic recognition and reconstruction of building models with LiDAR cloud points based on contours clustering[J].Bulletin of Surveying and Mapping,2013(10):23-25,29.

[17]李乐林,江万寿,张靖.利用极化角点指数进行数字曲线快速多边形近似[J].武汉大学学报:信息科学版,2009,34(12):1495-1498. Li L L,Jiang W S,Zhang J.Fast polygonal approximation of digital curve based on polarization cornerity index[J].Geomatics and Information Science of Wuhan University,2009,34(12):1495-1498.

(责任编辑： 李瑜)

Expanding research on CSG in 3D reconstruction from LiDAR

ZHA Dajian1, LI Lelin1, JIANG Wanshou2, HAN Yongshun1

(1.National-LocalJointEngineeringLaboratoryofGeo-SpatialInformationTechnology,HunanUniversityofScienceandTechnology,Xiangtan411201,China; 2.StateKeyLaboratoryofInformationEngineeringinSurveying,MappingandRemoteSensing,WuhanUniversity,Wuhan430079,China)

To tackling such problems as primitive decomposition, primitive recognition, model integration in 3D model reconstruction with LiDAR data by using the CSG method, this paper proposes an expanding method for CSG. In this method, the clustering property of building contours is used for layers partition and primitives decomposition, then the styles of the primitives is recognized by combining the features of contours clusters and the contour reconstruction results. In this way, the process of primitives automatic recognition in CSG method is achieved. According to the primitive recognition result, the corresponding reconstruction method for the segmentation is selected, and the whole 3D model for complex building is automatically reconstructed by integrating the segmentation models based on a set of effective model integration rules at last. Experiment results of a wide range LiDAR data show that the proposed expanding CSG method is effective in the 3D reconstruction of complex buildings with LiDAR data.

LiDAR; 3D reconstruction; CSG; primitive decomposition; primitive recognition; contour cluster; contour reconstruction

10.6046/gtzyyg.2016.04.06

査达剑,李乐林,江万寿,等.LiDAR三维重建中基于CSG方法的扩展研究[J].国土资源遥感,2016,28(4):35-42.(Zha D J,Li L L,Jiang W S,et al.Expanding research on CSG in 3D reconstruction from LiDAR[J].Remote Sensing for Land and Resources,2016,28(4):35-42.)

2015-07-10；

2015-12-16

国家自然科学基金项目“山地城市环境下等高线辅助的机载LiDAR点云复杂建筑物三维模型重建方法研究”(编号： 41401497)和湖南省科技计划项目“云计算环境下基于机载LiDAR数据快速获取高精度DEM的应用研究”(编号： 2015GK3027)共同资助。

TP 79

A

1001-070X(2016)04-0035-08

査达剑(1994-)，男，湖南科技大学测绘工程专业本科在读。

李乐林(1981-)，男，博士，讲师，主要从事机载LiDAR数据处理及高分辨率遥感影像处理方面的研究。Email: lilelindr@126.com。