Modern methods of underground hydromechanics with applications to reservoir engineering*

Hua XIANG, Valery V. KADET

Department of Petroleum and Underground Hydromechanics, Gubkin Russian State University of Oil and Gas, Moscow, Russia, E-mail: shidajundao@163.com

Modern methods of underground hydromechanics with applications to reservoir engineering*

Hua XIANG, Valery V. KADET

Department of Petroleum and Underground Hydromechanics, Gubkin Russian State University of Oil and Gas, Moscow, Russia, E-mail: shidajundao@163.com

In the report the basic principles of new approach to the study of transport processes in porous medium are represented. The “percolation” approach has arisen as an attempt to overcome the traditional phenomenological approach in the underground hydromechanics, based on the assumption of continuity of saturated porous media, which does not allow to explain and to model a number of effects arising from the fluids flow in porous media. The results obtained are very interesting not only from the scientific point of view but as the scientific basis for a number of enhanced oil recovery technologies.

fluid flow in porous media, percolation theory, relative phase permeability, oil field development, low salinity waterflooding

Introduction

The new approach aims to take into account for the description of fluid flow in porous media such details as structure of the pore space and the interaction of the fluids with the mineral surfaces. The mathematical foundation of this approach is the theory of percolation.

This approach has arisen as an attempt to overcome the traditional phenomenological approach in the underground hydromechanics based on the assumption of continuity of saturated porous media. The traditional approach does not allow to model, to describe and explain a number of effects arising from the fluids flow in porous media.

The new approach aims to take into account the description of fluid flow in porous media, especially the structure of the pore space and the interaction of the fluid with the surface of minerals. The mathematical foundation of this approach is the theory of percolation. The possibilities of the mathematical apparatusdeveloped are illustrated in the examples of the study of the fluid flow characteristics in reservoirs.

Transportation or conductive properties of porous media are determined primarily by the presence of conductive pore channels. The most simple and convenient model which allows describe the interaction of these channels and, as a result, to obtain the permeability of the porous medium as a macroscopic object-3-D lattice of conductive capillaries. It is natural to assume that the capillary radii in such lattice are distributed according to the actual porometrical curve-distribution density function of pore channel’s radii f( r). Given the distribution density function of the structure elements, the percolation modeling which allows to describe the conductivity of a heterogeneous medium, have been developed by the author[1,2].

1. General principles of the modern approach in the underground fluid mechanics

The approach based on a generalization of the Shklovsky-de Gennes model for an infinite cluster (IC) structure (Fig.1) in the case of the lattice containing conductive elements with the randomly distribution of their intrinsic value. Based on the representations of the IC structure, we have the problem of determining the conductivity of its skeleton which responsible forthe transport properties of IC and thus a porous medium as a whole.

Fig.1 Schematic representation of the IC structure in the Shklovsky-de Gennes model without taking into account a tortuosity (fractality) of its components

Conducting channels for the fluid flow are chains of hydraulically interconnected pore channels (capillaries) (Fig.2) of different radiir (conductivity σ～rλ, where exponentλis determined by nature of the transport process). The conductivity of the chainσ will be determined by the thinnest capillary, so it is natural to assume that this radius is the main characteristic of such a chain. Using it, we introduce the concept of “r-chain”-so we called the chain of capillaries, where the minimum radius of its capillaries is in the range r/ r +dr.

Fig.2 The scheme of conducting r -chains formation (Ris the correlation radius)

IC skeleton will be formed by r-chains within entire range of the functionf( r)and the number for eachr will have its own which is unknown in advance. Therefore it is necessary to construct an algorithm for determining the amount of the resulting r-chains, their conductivity and subsequent summation in order to find the total conductivity of the IC. That is, the algorithm is the main element of the percolation model.

The presented approach is based on the introduction of a specific systematization or hierarchy of rchains, which allows implement the above scheme of summation.

It can be shown that the concentration n(σ1)of conducting chains per unit cross-section area perpendicular to the selected direction composed of capillaries withσ≥σ1

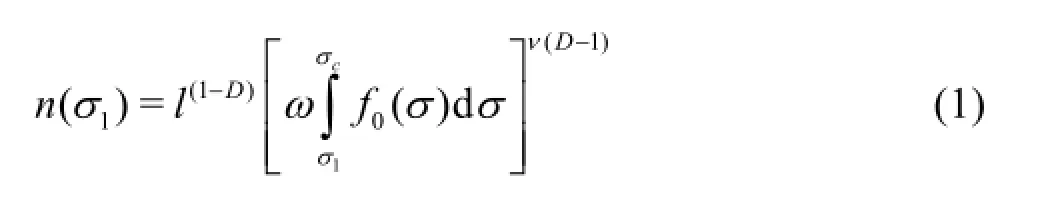
where critical conductivity σcis determined by percolation threshold

Accordingly, the distribution function for conducting chains by σ1is related to the value nin the ratiosincenincreases with decreasing σ1

Now determine k(σ1)is the average conductivity of the unit of the length of σ1is the chain composed of series-connected links with σ≥σ1(Fig.2). At this stage it is necessary to take into account the difference between 2-D and 3-D grids. In 2-D caserchains are smooth lines, so

However in 3-D grids significant tortuosity (fractality) of IC skeleton takes place. It can be shown that the actual length of the r -chain in more than times that normal linear distance between its ends.

Consequently the final expression for the average conductivity per unit length for the 3-D porous space is

Thus, using Eqs.(1)-(4), we obtain:

For 2-D lattice

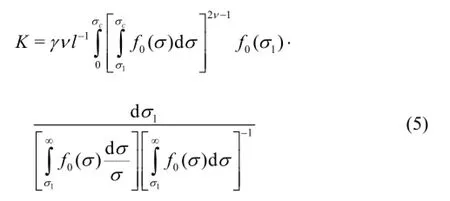
For 3-D lattice

The correction coefficient γ～1was obtained from comparison the analytical relations with the results of direct numerical simulation of the flow through the same network. In deriving expression (Eq.(6)) it was taken into account that numerical value of the tortuosity index associated with the fractal behavior of IC-skeletonζ=1.

The possibilities of the mathematical apparatus developed have been illustrated in the examples of the study of the fluid flow characteristics in reservoirs.

As it turned out the results obtained in the framework of this new so-called “percolation” approach are very interesting not only from the scientific point of view but as well from the practical point of view-they can serve as the scientific basis for a number of enhanced oil recovery technologies.

Capabilities of percolation modeling are demonstrated for a number of solving of topical application tasks where the various effects arising at the fluids flow in porous media are taken into account.

The greater the ratio of the surface area of fluid contact with solid to the volume of the moving fluid the more different from the usual for surround, or socalled “drop fluid flow.” That is why a model which allows calculate the effective viscosity of the electrolyte flow in porous medium must been built and very important to do it verification by comparison with experimental data. In this work the method of calculation for effective viscosity of mineralized water flowing in a porous medium is considered.

A percolation model is suggested for the electrokinetic flow of a binary electrolyte solution in a porous medium. The effects of the ion concentration in the solution, the zeta potential of the surface of the pore space, and the shape of the porosimetric curve on the filtration flow velocity are analyzed. Experiments have been designed and carried out to verify the model. The results of theoretical calculations and experimental data are in good agreement.

Accordingly it is shown that the design of the development should take into account that the value of the droplet fluid flow viscosity can differ very significantly from its effective viscosity for fluid flow in porous media.

2. The effective viscosity of mineralized water flowing in porous medium

The greater the ratio of fluid-solid contact area to the flowing fluid volume the more fluid flow unlike to conventional or so-called “drop fluid flow.”

In a number of experiments to investigate the flow of fluids in porous media[3-5]mentioned the excess of observed in the experiment viscosity (“effective” viscosity) as compared to its value for the classical droplet. Moreover, features of the flow in microchannels depend on the nature of the fluid and geometric parameters of the channel.

In the model[6]has been built which allows calculate the effective viscosity of the electrolyte flow in porous medium and the verification by comparison with experimental data has been performed.

Let the fluid flowing through the grid under the influence of the applied pressure gradient is symmetrical electrolyte solution having a dielectric constantε and viscosityµ. Moreover zeta-potentialζis arising on the capillary wall.

In order to relate flow macroparameters to microparameters of the medium, we will firstly derive a relationship between pressure drop across the bed of the medium and the liquid flow rate in each liquid-conducting path of this system. As a first step, we will consider a separate channel with radiusa(Fig.3).

Mass force in such a system will be determined by the interaction of the streaming potentialφand charge of the ion cloud with bulk density ρe. Thus, the steady state flow in the capillary is described by Navier-Stokes equation of the following formwhereu is the flow rate,µis the dynamic viscosity coefficient of the liquid drops,∇pis the pressure gradient,∇φis the streaming potential gradient along the axis of the channel. The bulk density of the charge ρeis determined by Poisson equation

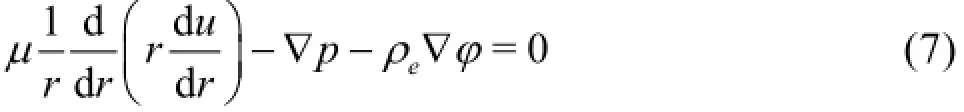
Fig.3 Scheme of elektrokinetics flow in the capillary channel

where ε0is the dielectric constant for vacuum, andψ is the potential of electrical double layer (EDL).

Substituting Eq.(8) into Eq.(7) and integrating with the following boundary conditions:u( a)=0 (slip condition),ψ(a)=ζ(the condition of equality of the zeta potential on the wall of the channel to value ζ),u′ (0)= ψ′(0)=0(conditions of cylindrical symmetry of the decision). As a result, we obtain an expression for the flow rate in the channel, which take into account the impact of EDL potential

Taking for the local concentration of ions the Boltzmann distribution lawwhere n0is the the total volume concentration of ions after the integration of the Eq.(9) in the area of the channel cross section, we obtain expressions for the volumetric flowq and the currentI

Here ∆p =∇pland ∆ϕ=∇ϕl. The coefficients L11, L12,L21,L22depend on fluid properties and channel dimensions

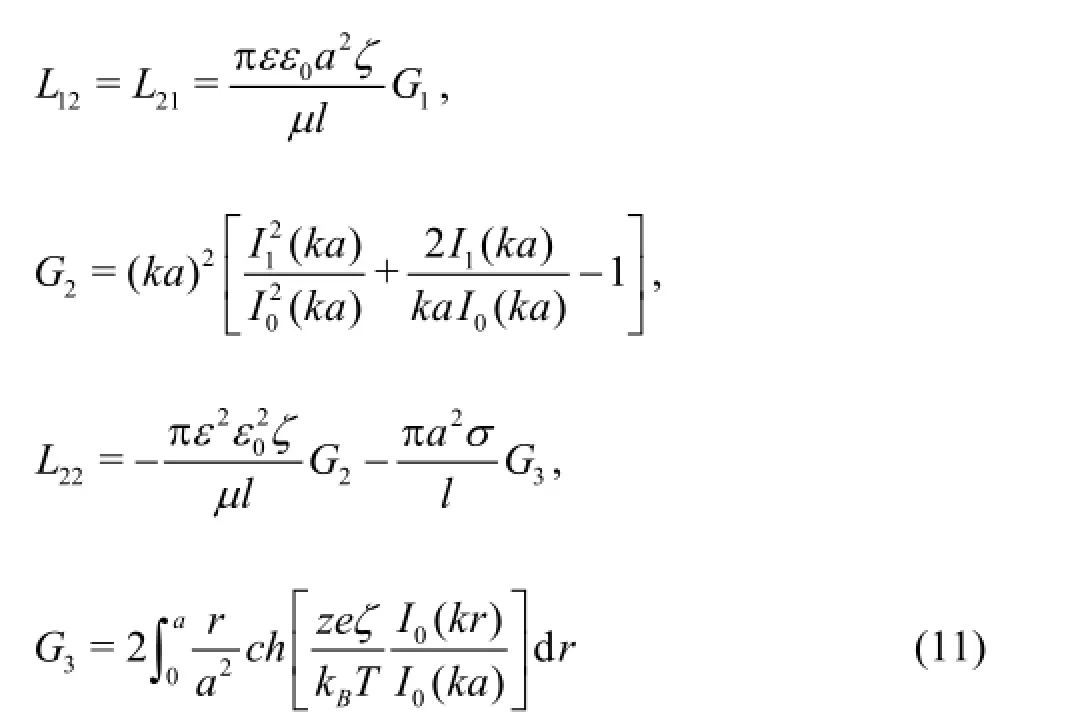
where1/k is the EDL thickness in terms of the Debye-Huckel parameteris the modified first-kind Bessel function of zero order and kaconventionally called the dimensionless electrokinetic radius (ratio of the channel radius to the EDL thickness).

For the steady-state electrokinetics flow in the channel, the conduction current is equal to the steaming current, therefore, the total currentI in Eq.(10) is zero. In accordance with the principle of Onsager L12= L21, and the pressure drop at the channel ends is

The summation of the flow rates and pressure drops across all pathways using (Eqs.(10)-(12)) yields the following filtration law

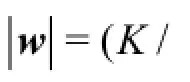
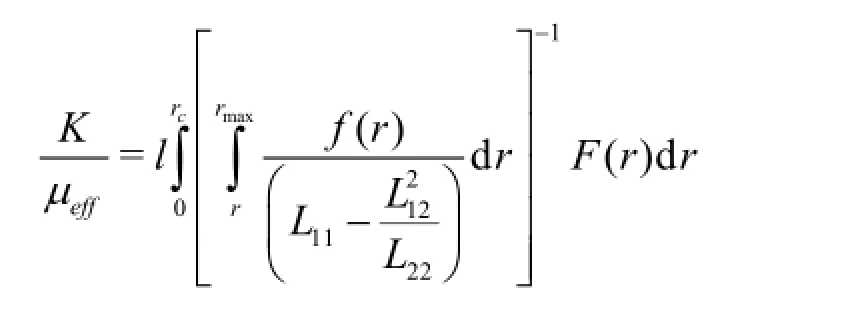
hence

Taking into account the expression for the permeability of the porous medium Eq.(6) from Eq.(14) we obtain the expression

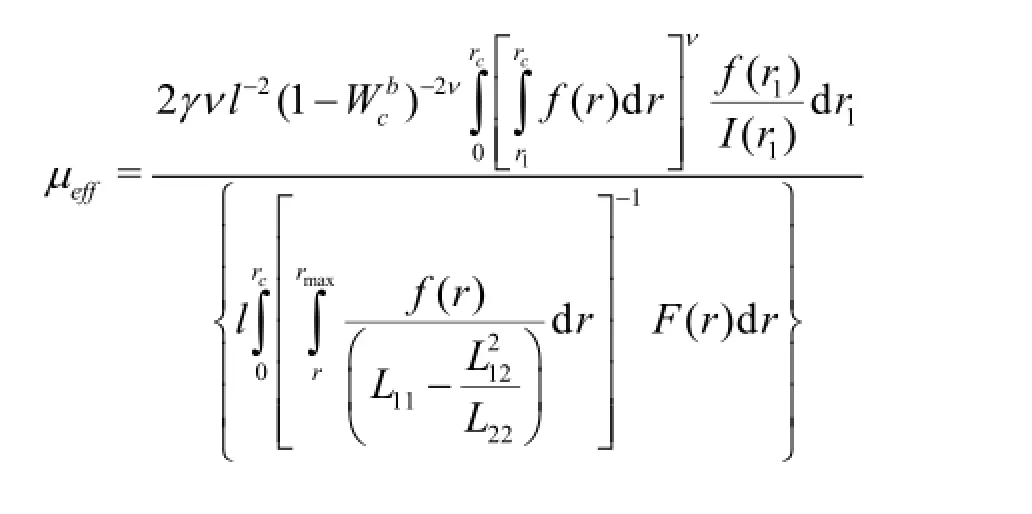
for the effective viscosity of the electrolyte flowing in the porous media.

Fig.4 The dependence µef f/µ(ζ=0)of the average electrokinetic radius for fixed rmin(ζ=100 MВ,n0= 6.022× 1022,ζ=150 MВ,n0=6.022× 1021,ζ= 200 MB,n0 = 6.022× 1020,T =293 K)

Figure 4 shows the results of calculations of the value µθ/µ0in the case of the constant minimum radius (rmin=10-7m)and the varied maximum radius of distribution density functionf( r).

It can be seen that the effect of EDL on the fluid flow increases with amount of the capillaries with a smaller radius. It has been established that in case the presence of a sufficient number of channels with a radius comparable to the thickness of EDL, the flow rate of the electrolyte is significantly less (several times) than predicted by the theory which not taking into account the impact of EDL. We can interpret this fact as an increase in viscosity (effect of “elektroviscosity”). The calculation results are in good agreement with those of the author’s experiment.

Accordingly, the design of the development should take into account that the value of the droplet fluid flow viscosity can differ very significantly from its effective viscosity for fluid flow in porous media.

3. Percolation analysis of relative permeability hysteresis behavior

During the process of developing the oil field using such methods as cycling water flooding and changing the flow direction the displacement of oil by water is changed into the displacement of water by oil and vice versa. Such change in flow character affects on relative permeability as function of water saturation. This phenomenon is called relative permeability hysteresis in drainage and imbibition.

Neglecting of the phenomenon in the hydrodynamic modeling of oil fields developing leads to significant errors.

Presence of relative permeability hysteresis was noted in a number of experimental investigations[7-9]. The mathematical model of this phenomenon was constructed and studied in Refs.[10,11].

Fig.5 Profiles of oil-water contact in a capillary for drainage (on the left) and for imbibition (on the right) with indication of displacement direction

Fig.6 Comparison of experimental and calculated with hydrophobisation model and with plastic model relative permeability curves for a sample 114 (dolomite) and for a sample 4 (calcite)

The following phenomena were chosen for the main mechanisms of hysteresis origin. In the process of drainage active oil components are adsorbed on the surface of the rock-forming minerals[7]. It leads to oil nanofilms formation, which does not change the form of f( r)function, as the film thickness is several orders smaller than the radius of the smallest capillaries. As a result it causes two possible effects, which are considered in the model. The first is surface hydrophobisation and the second-changing of plastic properties in both fluids. The second effect also occurs because of mixing oil and water during drainage, when some oil components get into water.

As a result of the oil flow through porous medium initially hydrophilic surface properties of some part of capillaries are changed. To describe this phenomenon the percolation model of a medium with microheterogeneous wettability was used[5,6,9,10], where two parametersκanda were introduced:κis the share of capillaries with unchanged surface properties (type 1), (1- κ)is the share of capillaries with changed surface properties (type 2),a=cosθ2/cosθ1,θ1and θ2are the wetting angles in capillaries 1stand 2ndtype, respectively. Thus the surface properties may be changed in two principally different ways (Fig.5): either hydrophilicity is decreased (0＜a＜1), or capillary surface properties become hydrophobic at all(a＜0).

Thereby the calculation technique[10,11]enables to calculate relative permeability as a function of water saturation for porous media with microheterogeneous wettability.

Percolation model of relative permeability hysteresis after plastic properties of the fluids changing isbased on percolation model for fluids with different plastic properties[1]. According to this model we assume water to be Newtonian fluid during drainage and pseudoplastic fluid during imbibition. If oil has pseudoplastic properties during drainage it becomes Newtonian during imbibition and if it is Newtonian fluid during drainage it becomes pseudoplastic or Binghamian plastic fluid during imbibition. Expressions for the relative permeabilities are built in the same way, taking into account the consequence rheological properties of the fluids for the law flow in a separate capillary.

The experimental curves and calculation results obtained are based on the above models and represented on Fig.6 for two samples[9].

Represented model has rather universal nature and enables to consider different mechanisms of porous media surface properties change. The best accordance with referred experiment is achieved by using hydrophobization of part of porous media during water displacement by oil as the first mechanism and oil and water plastic properties change as the second mechanism. Values of parameters for pore space hydrophobization as well as for plastic properties change of fluids for concrete process are determined by comparison of calculated relative permeability curves and experimental data.

Further represented methodology can be used for relative permeability calculation for any porous media and for any plastic fluids having only mineral composition data and differential radius distribution curve f( r). Experimental core research for the purpose of relative permeability curves determination requires a considerable amount of time in contrast to experimentalf( r)measurements. Having carried out relative permeability hysteresis behavior classification for different mineral composition samples it is possible to determine the parameters of pore space hydrophobization and rheological properties change of fluids. Thus on the basis of presented methodology one can calculate relative permeability with hysteresis using these values and measuring f( r).

In future we are going to build a generalized model including both of considered mechanisms. The results obtained in this paper allow suggest that such model will be in better accordance with the experiment.

The phenomenon of relative permeability hysteresis is observed during the process of developing the oil field by methods where the flow direction changes and the displacement of oil by water changes into the displacement of water by oil and vice versa. This paper represents the model of relative permeability hysteresis for drainage and imbibition based on percolation theory.

The phenomenon of active oil components adsorption on the rockforming minerals is chosen for the first mechanism of hysteresis origin. In the process of drainage this causes surface hydrophobization of initially hydrophilic rock which leads to each phase relative permeability change. To describe this phenomenon percolation model for media with microheterogeneous wettability is used. The second mechanism is plastic properties change, described by percolation model for fluids with different plastic properties.

Received numerical solution is represented as relative permeability curves and is qualitatively confirmed by the experimental data. The behavior of relative permeability hysteresis is observed and analyzed for various differential radius distribution curves, capillary network coordination numbers, saturation models, hydrophobization degree and plastic properties. It allows obtaining general tendencies of relative permeability hysteresis behavior. Further introduced methodology can be put into practice for relative permeability calculation considering hysteresis in any porous media to reduce the time spent.

4. Effect of ion exchange processes on two-phase flow of oil and mineralized water in clay reservoirs

It is known that after violation of the chemical equilibrium in the “solution-rock” system clay minerals vary in volume under the action of osmotic and ion exchange processes, which significantly affects the properties of clay-containing reservoir rocks. In addition, the changing of the reservoir hydrochemical regime may lead to a change in the type of clay mineral, entailing the destruction of the crystalline structure of clay and disaggregation. Apart from the salt concentration in the water, hydration of the clay minerals also depends on the combination of the salts in solution.

For example it was shown that ion exchange process at the interface between rock and displacing agent lead to an increase in relative permeability to oil and decrease in relative permeability to water. The growth in relative permeability to water and its reduction to oil is caused by ion exchange processes leading to clay contraction. This is why swelling of clay leads to enhanced oil recovery-relative permeability to oil increases when injecting electrolytic solutions with highly active metal ions.

In recent years, a growing interest in tertiary methods of oil field development, called Low Salinity Waterflooding (LSW), takes place[12]. This method allows to get more oil from the reservoir by pumping desalinated water or water of different chemical composition that the reservoir. Although the reasons for the growth of oil under these conditions until today has not been fully investigated, most researchers attributing the oil increasing with a high ion exchange capacity of clay minerals.

The conditions under which recorded an increase displacement efficiency in the application of LSW have been defined in a number of experiments on different core material[12-14]. Among them

(1) A significant proportion of clay minerals in the rock.

(2) Produced water contains divalent cations Ca2+or Mg2+.

(3) Injected water has a reduced concentration of salts in comparison with the formation water.

Calculation of the effect of the injection into the reservoir the water with a different salinity from the salinity of produced water is presented in Ref.[15]. The effect of osmotic and ion exchange processes on twophase flow of oil and electrolytic solutions in clay reservoirs has been calculated. The analysis was carried out and it was shown that changes in filtration-capacitive properties (FES) of clay-containing reservoir in the process of changing the hydrochemical regime of reservoir development take place. The results are summarized in Figs.7, 8.

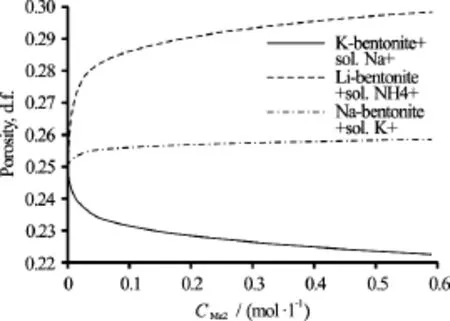
Fig.7 The dependence of the porosity of clay-containing rocks with different composition of exchangeable cations on the composition and concentration of salts in the injected fluid

Fig.8 Relative permeability curves for water and oil in claycontaining formations with different exchangeable cations, depending on the composition of salts in the injected fluid

It was found that the porosity may vary between 15%-20% depending on the salt concentration and the ionic composition of the solution and the exchange complex of the clays.

Figure 8 shows the effect of ion exchange processes for relative permeability curves (RPC) at a salt concentration in the electrolyte CMe2=0.5 mol/l.

Calculations show that due to the shrinkage of clay by reacting Na-bentonite with a solution of potassium chloride, there are the growth of water phase permeability and decrease of oil phase permeability. Due to the swelling by reacting K-bentonite with sodium chloride solution there are a decrease in permeability for water and growth for oil. The results of the theoretical calculations are confirmed by experimental studies of the RPC behavior in clay-containing layers for various electrolyte solutions.

Due to the fact that after swelling of clays, the reservoir gets more fine-pored one must take to account the capillary forces. Therefore filtration of fluids considered in frame of Rappoport-Lease model, and a complete system of differential equations in partial derivatives to determine the salt concentration of the electrolyte C and a water saturation S has the form

where Sris the proportion of adsorbed water in the rock (“+” sign for Srof swelling clays, “-” in the case of shrinkage),F( S, C)is the function ofBuckley-Leverett,q is the total consumption of the phases,Pk( S, C)is the capillary pressure function, J( S)is the Leverett function,χis the surface tension coefficient,Mi( S, C)is the mobility of phases, wiis the filtration rate of phases,∆Piis the the difference between the pressure on the contour and the wall borehole in thei -thphase,Rkis the radius of the reservoir external boundary,rwis the well radius,K( C)is the absolute permeability,f[ r( C)] is the porometrical function,γ′is the factor reflecting the presence of flows between the conducting chains (order of unit),v′is the index of the correlation radius,rcis the critical radius of the capillary,lis the average length of the capillary,D∗is the factor including diffusion and hydrodynamic dispersion, R′( C)is the hydration rate. We neglect the influence of gravitational forces.

Figure 9 shows oil recovery depending on development time.

Fig.9 Oil recovery depending on development time in case of low salinity waterflooding and electrolytic solution waterflooding

Fig.10 Concentration of electrolyte on external boundary depending on development time (T is the formation water injection time,t is the electrolytic solution injection time)

Cyclic injection of the electrolyte solution (Fig.10) is considered to be more cost-effective than the constant one. In this regard we have discussed various realizations of electrolyte solutions periodic download (Fig.11).

Fig.11 Oil recovery depending on frequency of electrolytic solutions injection ω=t-1

It’s shown that cyclic injection of electrolytic solutions with highly active metal ions (i.e. LiCl) allows save 50% of salts and increases oil recovery by 8.5% (i.e. LiCl) and 7% (i.e. NaCl) in comparison with formation water injection.

The analysis of ion exchange processes in claycontaining porous medium allows determine the reasons for the growth of oil recovery when changing the hydrochemical regime of reservoir[16].

It’s been shown that ion exchange process at the interface between rock and displacing agent leads to an increase in relative permeability to oil and decrease in relative permeability to water. The growth in relative permeability to water and its reduction to oil is caused by ion exchange processes leading to clay contraction. This is why swelling of clay leads to enhanced oil recovery-relative permeability to oil increases when injecting electrolytic solutions with highly active metal ions.

Due to the ion-exchange swelling and contraction of clays the porosity may change about 10%-15%. This is also the reason why oil recovery increases. When porosity of reservoir decreases, the reservoir works like a sponge, squeezing out oil from reservoir.

Calculations show that electrolytic solutions injection increases oil recovery up to 10% in comparison with formation water injection. Cyclic injection of electrolytic solutions with highly active metal ions (i.e. LiCl) allows to save 50% of salts and increases oil recovery by 8.5% (i.e. LiCl) and 7% (i.e. NaCl) in comparison with formation water injection.

The created model allows evaluating the influence of injected agent composition on technological performance of clay-containing reservoirs development.

5. Conclusion

Results of theoretical analysis and experimentalinvestigation for transport in porous media are presented. A new approach to modeling of transport in porous media is developed and a number of new percolation models is considered. The models allow obtain analytical correlations for relative phase permeabilities for different porous media. Different methods of intensification of economic minerals based on new physical effects of reconstruction of the rock’s pore space structure are analyzed.

[1] Selyakov V. I., Kadet V. V. Percolation models for transport in porous media. With applications to reservoir engineering [M]. Dordrecht, The Netherlands: Kluwer Academic Publishers, 1996.

[2] Kadet V. V., Maximenko A. A. Determination of relative permeabilities using the network models of porous media [J]. Journal of Petroleum Science and Engineering, 2000, 28(3): 145-152.

[3] Tuckermann D. B., Pease R. F. W. High-performance heat sinking for VLSI [J]. IEEE Electron Device Letters, 1981, 2(5): 126-129.

[4] Pfahler J. N. Liquid transport in micron and submicron size channels [D]. Doctoral Thesis, Philadelphia, USA: University of Pennsylvania, 1992.

[5] Peng X. F., Peterson G. P., Wang B. X. Frictional flow characteristics of water flowing through rectangular microchannels [J]. Experimental Heat Transfer, 1994, 7(4): 249-264.

[6] Kadet V. V., Koryuzlov A. S. Effective viscosity of mineralized water flowing in a porous medium: Theory and experiment [J]. Theoretical Foundations of Chemical Engineering, 2008, 42(6): 899-904.

[7] Dernaika M. R., Basioni M. A., Dawoud A. et al. Skjæveland/Variations in bounding and scanning relative permeability curves with different carbonate rock types [C]. The 2012 Abu Dhabi International Petroleum Conference and Exhibition (SPE 162265). Abu Dhabi, UAE, 2012.

[8] Wei J. Z., Lile O. B. Influence of wettability and saturation sequence on relative permeability hysteresis in unconsolidated porous media// [EB/OL]. http://www.onepetro.org/mslib/app/Previewed paper Number = 00 025282 & society Code = SPE, 1993, SPE-25282-MS.

[9] Braun E. M., Holland R. F. Relative permeability hysteresis: Laboratory measurements and a conceptual model [J]. SPE Reservoir Engineering, 1995, 10(3): 222-228.

[10] Kadet V. V., Galechyan A. M. Percolation model of relative permeability hysteresis [J]. Journal of Applied Mechanics and Technical Physics, 2013, 54(3): 423-432.

[11] Kadet V. V., Galechyan A. M. Percolation modeling of relaive permeability hysteresis [J]. Journal of Petroleum Science and Engineering, 2014, 119(54): 139-148.

[12] Tang G. Q., Morrow N. R. Influence of brine composition and fines migration on crude oil/brine/rock interactions and oil recovery [J]. Journal of Petroleum Science and Engineering, 1999, 24(2): 99-111.

[13] Lager A., Webb K. J., Black C. J. J. et al. Low salinity recovery-an experimental investigation [J]. Petrophysics, 2008, 49(1): 28-35.

[14] Korrani A. K. N., Jerauld G. R., Sepehrnoori K. et al. Coupled geochemical-based modeling of low salinity waterflooding [C]. Society of Petroleum Engineers-19th SPE Improved Oil Recovery Symposium. Tulsa, Oklahoma, USA, 2014.

[15] Kadet V. V., Chagirov P. S. Investigation of cyclic electrolytic solutions injection in clay-containing oil reservoirs [J]. Journal of Petroleum and Environmental Biotechnology, 2015, 6(5): 1000242.

[16] Kadet V. V., Maximenko A. A. The deposition in network models of porous media [C]. 16st IMACS World Congress on Scientific Computation, Applied Mathematics and Simulation. Lausanne, Switzerland, 2000, 712.

(Received June 22, 2016, Revised October 27, 2016)

* Biography:Hua XIANG (1988-), Male, Ph. D.

Valery V. KADET,

E-mail: kadet.v@gubkin.ru