新一维混沌系统及加密特性研究

李娟霞 孙会明 陈 薇

1(河西学院物理与机电工程学院 甘肃 张掖 734000)2(西安科技大学电气与控制工程学院 陕西 西安 710054)



新一维混沌系统及加密特性研究

李娟霞1孙会明2*陈 薇2

1(河西学院物理与机电工程学院 甘肃 张掖 734000)2(西安科技大学电气与控制工程学院 陕西 西安 710054)

提出一种新的产生一维混沌系统的组合结构，以此结构设计两个新一维混沌系统，通过绘制Lyapunov指数图和分岔图研究两个新混沌系统性能。研究结果表明，此结构生成的一维混沌系统具有混沌区间大、区间连续、混沌序列分布均匀、系统Lyapunov指数高和可控参数多等优点。为了进一步提高混沌序列均匀分布特性，设计一变换过程，变换之后的混沌序列满足均匀分布。最后，为了展示新系统在信息安全方面的应用，设计一简单的图像加解密算法。通过Matlab软件进行仿真和性能测试，结果表明变换之后的混沌序列具有更好的加密特性。

混沌 图像加密 统计分析

0 引 言

混沌系统对参数和初始值具有很强的敏感性，且具有遍历和不可预测的特点；混沌系统通过控制其参数和初始值就可以很方便地产生不同的伪随机序列。因此，混沌系统在不同领域的应用引起了很多研究者的关注。特别在信息安全方面的应用，混沌系统展示了极其优越的性能[1-23]。例如，由Hua等人提出的2D Sine-Logistic调制混沌图像加密算法[1]，其对图像加密获得了较高的安全性。

现存的混沌系统主要分为两类：一维混沌系统和高维混沌系统。一维混沌系统通常含有一个变量和比较少的参数，例如Logistic、Sine、Tent映射等[2,3]，它们的结构和混沌轨迹相对简单。随着混沌信号估计技术的发展，当很少的信息被获取之后，它们的混沌轨迹就有可能被识别，进而获得系统的初始值和控制参数值，这些缺点限制了它们在安全领域的应用。已有文献研究指出，几种基于一维混沌映射图像加密算法是不安全的[4]。高维混沌系统至少有两个变量，与一维系统比较，高维混沌系统如Lorenz系统、chee-Lee系统具有更复杂的系统结构和更好的混沌行为。这些特点将使得高维混沌系统的轨迹变得很难预测。然而，高维系统的实现变得相对复杂，也使得高维系统的应用受到限制。一维混沌系统普遍存在Lyapunov低的现象，而且一维混沌系统都存在混沌区间小、混沌区间不连续和混沌序列分布不均匀的问题。研究如何通过有效的方法获得混沌区间宽、混沌区间连续、混沌序列分布均匀且具有高Lyapunov指数的一维混沌系统具有很高的研究价值。

设计新混沌系统极其困难，如何通过有效的方法在现有一维混沌基础上获得性能更好的一维混沌系统不失为一捷径。文献[2]提出了一种并联组合方式，通过此方式可以改善混沌系统的混沌序列分布不均匀、混沌区间不连续和混沌区间小的问题，但是生成的新混沌系统的Lyapunov指数并没有提高。文献[5]提出了一种级联结构，通过对子(Sine、Logistic、Tent等)一维系统进行级联则可以提高系统的Lyapunov指数，且混沌区间也有所增加，但是混沌区间不连续问题和混沌序列分布不均匀问题没有得到改善。

本文在一维混沌系统的基础上，提出一新的能产生一维混沌系统的结构。该结构所描述的方式对现有一维混沌系统(Sine、Tent、Logistic等)进行组合可以获得性能更好的一维混沌系统，且其结构简单灵活。文章中以此结构给出了两个新的一维混沌系统，为观察新混沌系统的混沌行为，通过Matlab软件绘制了对应的分岔图和Lyapunov指数图。结果表明，新的一维混沌系统具有更高的Lyapunov指数，产生的混沌序列分布更加均匀，混沌区间广、混沌区间连续且可控参数多。本文同时对设计的两个新混沌系统之一提出一种序列均匀分布改善方法，对改进后的混沌序列做了均匀分布性能测试。测试结果表明，输出混沌序列通过改善之后满足均匀分布。为了展示新混沌系统和改善之后的混沌序列的加密特性，设计一简单的图像加密算法，仿真结果表明新混沌系统产生的混沌序列具有很高的加密特性。

1 典型一维混沌系统

本文研究主要以一维Logistic、Tent和Sine混沌映射为基础。因为Logistic、Tent和Sine系统的混沌参数u和xn取值区间相同，而其他一些一维混沌系统尽管u和xn取值不相同，但是都可以通过变换使其相同[5]。Logistic、Tent和Sine系统表达式如下：

Logisticmap:xn+1=uxn(1-xn)

(1)

(2)

Sinemap:xn+1=λsin(πxn)/4

(3)

已有研究表明：Logistic、Tent和Sine混沌区间范围窄、混沌序列分布不均匀，且Logistic和Sine混沌区间不连续[2]。

2 新一维系统构造方法

文献[2]的研究结果表明对一维系统进行适当的组合有助于改善单一一维混沌系统混沌区间不连续的问题；文献[5]的研究结果表明，级联有助于提高混沌系统的Lyapunov指数。新一维系统产生结构如图1所示，它是对一维混沌系统进行非线性组合而获得的；组合表达式如式(4)所示，组合的条件是混沌参数取值区间相同且值域相同。绘制分岔图和Lyapunov指数图采用文献[3,6,7]中方法。

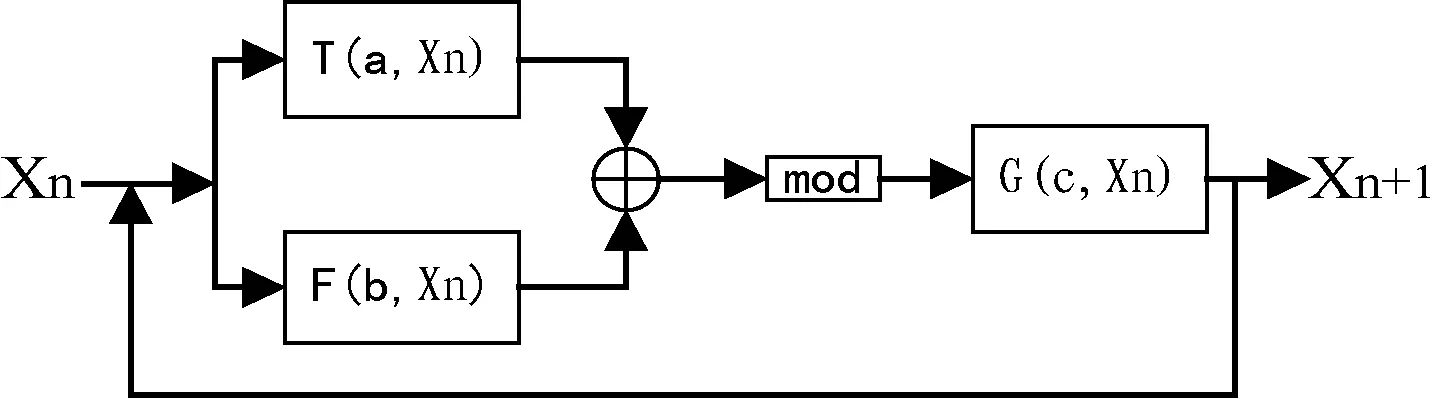
图1 新混沌系统结构图

Newsystem:Xn+1=G(c,(T(a,Xn)+F(b,Xn)mod1))

(4)

其中T(a,Xn)、F(b,Xn)和G(c,Xn)都是一维混沌系统(子系统)，a、b和c为系统参数，mod为取模操作，n是迭代次数。

(1) L-LSS(Logistic-Logistic Sine System)

选择T为Logistic映射、F为Sine映射、G为Logistic映射构造新的一维混沌系统如式(5)所示：

Xn+1=u1·{mod(uXn(1-Xn)+(4-u)sin(πXn)/4,1)}·

{1-mod(uXn(1-Xn)+(4-u)sin(πXn)/4,1)}

(5)

其中u、u1为控制参数，设u1=4为固定值，u∈[0,4]绘制对应的分岔图和Lyapunov指数如图2所示。

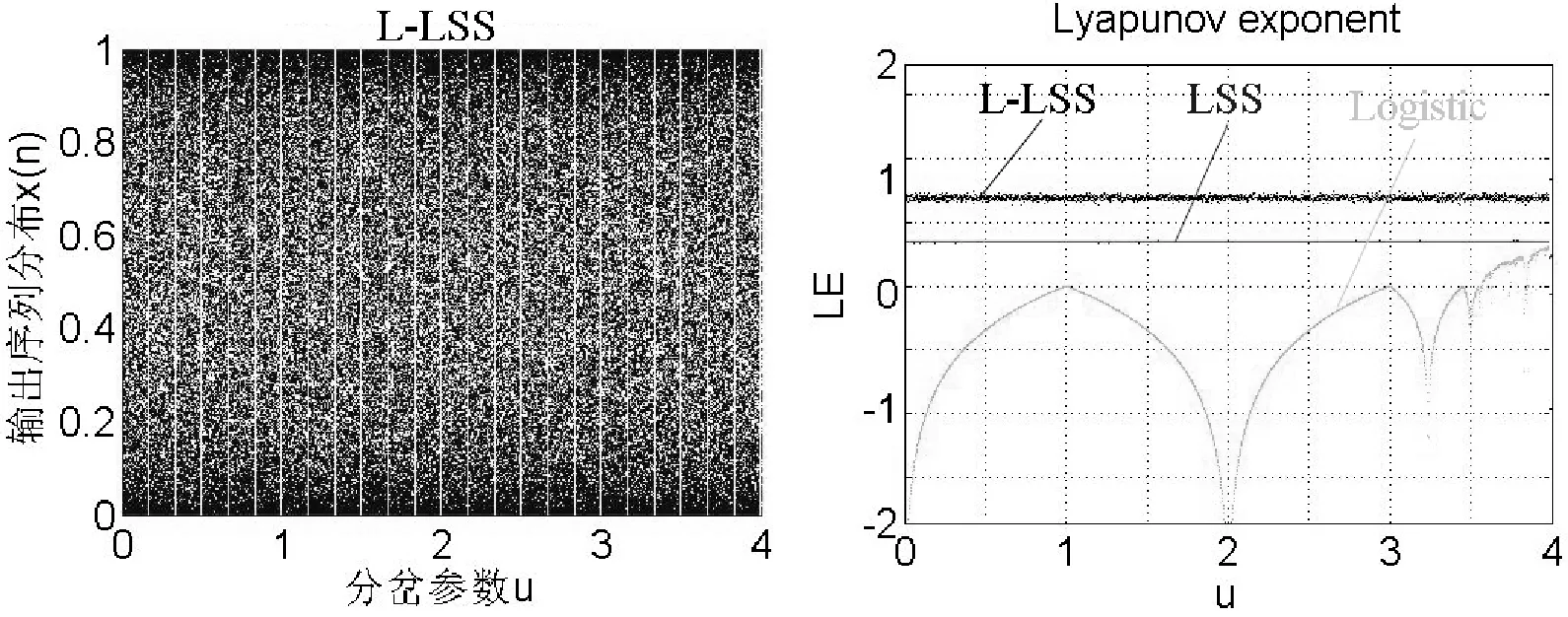
图2 L-LSS系统的分岔图与Lyapunov指数图

(2) S-LSS(Sine-Logistic Sine Syetem)

选择T为Logistic映射、F为Sine映射、G为Sine映射构造新的一维混沌系统如式(6)所示,对应的分岔图和Lyapunov指数如图3所示。

Xn+1=u1·sin{((uXn(1-Xn)+(4-u)sin(πXn)/

4)mod1)·π}/4

(6)

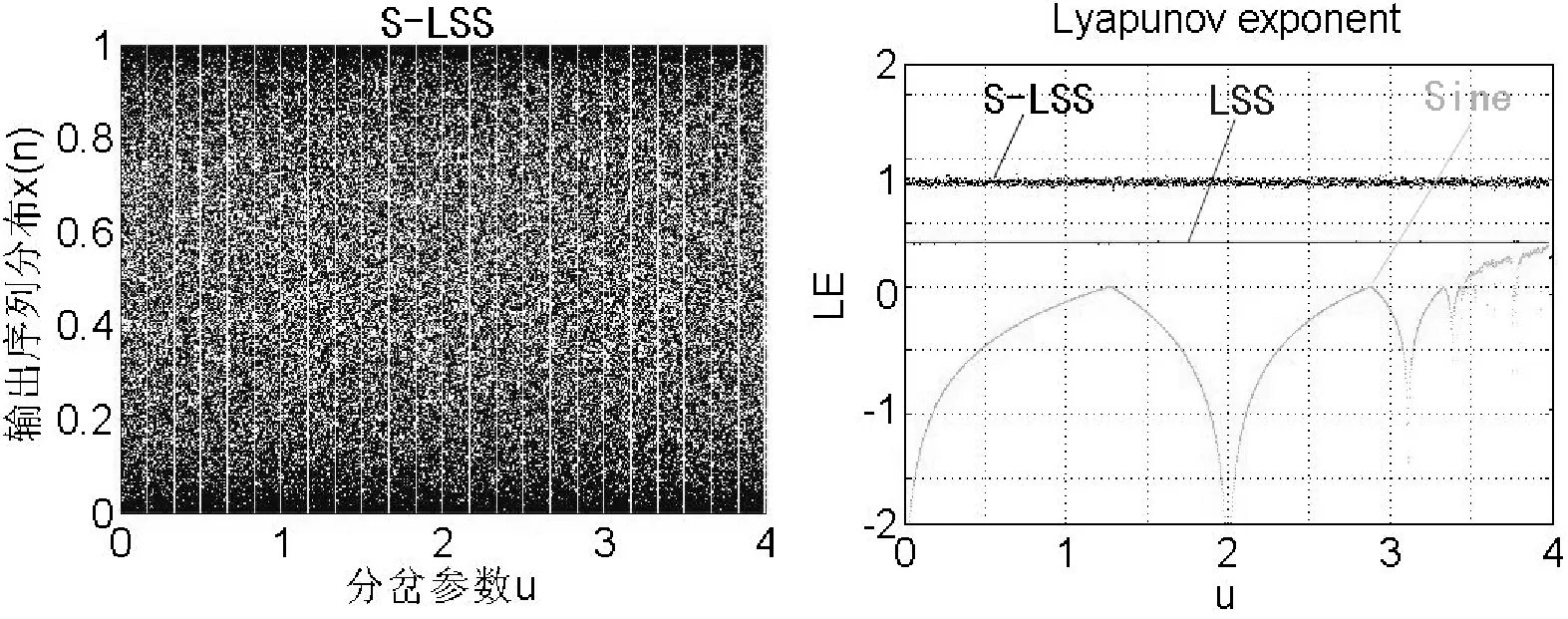
图3 S-LSS系统的分岔图与Lyapunov指数图

由图1构造的新一维系统L-LSS和S-LSS分岔图和Lyapunov指数图可以看出，新系统在参数u∈[0,4]区间都是混沌的，不存在周期窗口现象。新L-LSS和S-LSS系统的Lyapunov指数与Logistic映射和LSS[2]映射Lyapunov指数比较，发现新系统具有更高的Lyapunov指数，对初始值与参数的敏感性更高，混沌序列的分布均匀性得到了改善。

因此，采用新系统设计的混沌加密算法理论上具有更高的安全性。同时观察三者的关系发现，L-LSS系统的Lyapunov指数近似等于Logistic映射与LSS映射Lyapunov指数之和，S-LSS系统的Lyapunov指数近似等于Sine映射与LSS映射Lyapunov指数之和，与文献[5]的研究结论一致。具体的Lyapunov指数数值如表1所示。

表1 Lyapunov指数

表1获得的Lyapunov指数为最大Lyapunov指数，且除了混沌系统不同以外，其他计算条件相同。

图1的构造方法可以增加新系统的Lyapunov指数，同时可以使混沌系统混沌区间增加，混沌序列的分布均匀。观察L-LSS系统与S-LSS系统分岔图发现，L-LSS和S-LSS系统产生的混沌序列尽管比单一一维系统的混沌序列分布均匀很多，但是仍然不是均匀分布的。由对应分岔图中0和1附近颜色较深可以看出，0和1附近序列值比较多。如果一个混沌系统产生的混沌序列分布满足均匀分布，则采用此序列进行加密可以获得更高的安全性[8]。

以上提出的组合结构只要是满足上面提到的组合条件,则可以将任何不同一维混沌系统通过以上组合来获取新的性能更好的一维混沌系统。对于不满足组合条件的系统则可以通过变换使其满足条件之后，再进行组合。因此，此结构有很大的灵活性。Tent一维系统直接可以与Sine和Logistic进行组合，具体的表达式此处不再给出。

3 序列分布不均匀改善及统计分析

本文以新系统L-LSS系统为例，L-LSS系统产生的混沌序列对应的直方图如图5(a)所示。直方图分布反映的结果与从分岔图表现的结果相同，0和1附近序列值比较多，直方图表现为0和1附近存在尖峰。以文献[8]的思想为基础，对L-LSS产生的混沌序列作式(7)变换，变换之后的序列直方图如图4(b)所示。

(7)

图4 混沌序列直方图

由直方图可以明显看出，变换之后的混沌序列分布变得非常均匀，具有似噪声的特点。为了更进一步分析其性能，绘制序列的自相关特性图如图5所示。图5同时绘制了Logistic映射和随机函数生成序列的自相关特性图，比较三者发现，T(L-LSS)变换之后的混沌序列分布更加均匀且随机性更好。

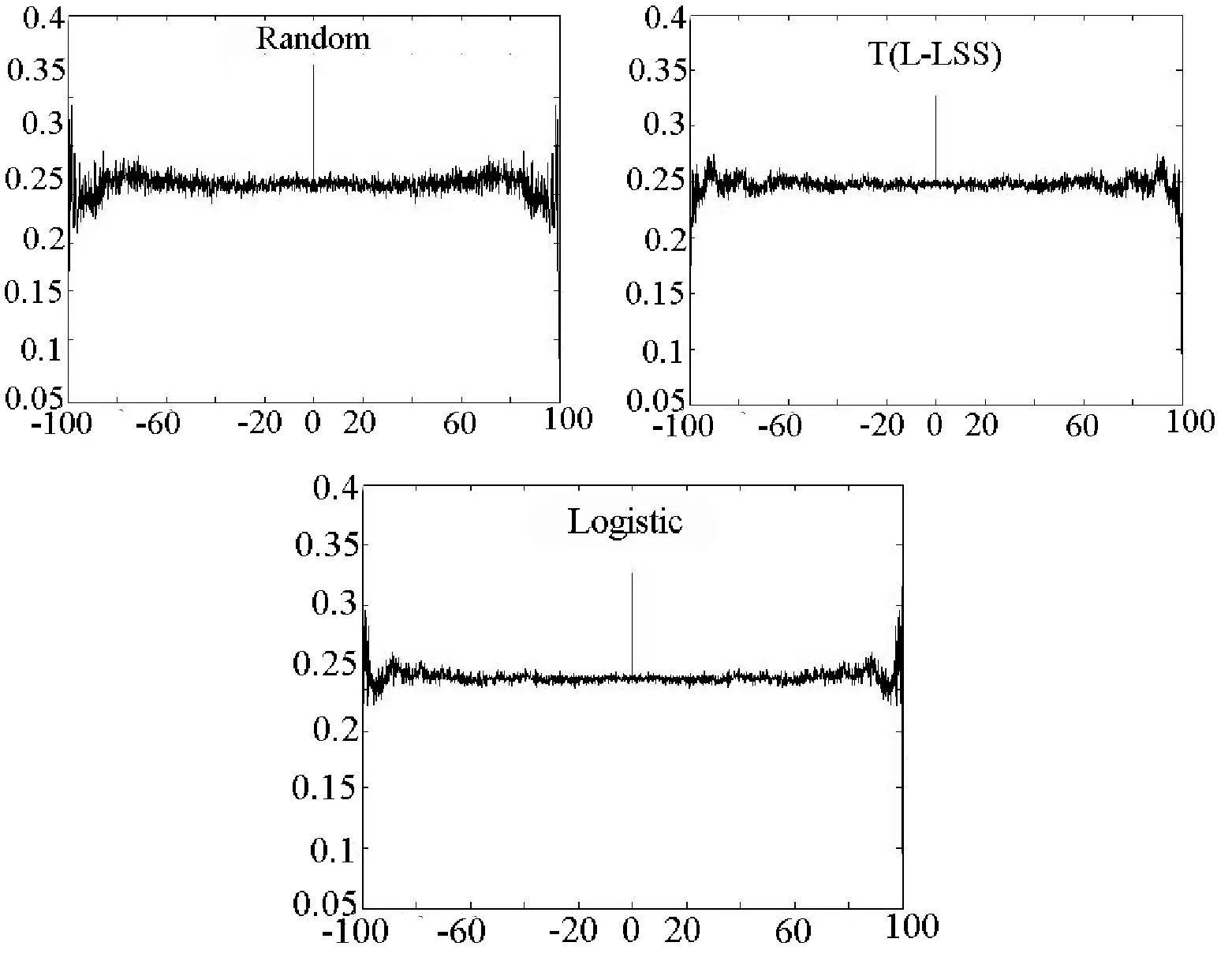
图5 自相关仿真

3.1 T(L-LSS)混沌序列概率分布

(8)

方差D(X)的计算公式为：

(9)

期望E(X)和方差D(X)是随机变量X两个非常重要的数字特征。在实际的应用当中，不一定非要求出X的对应概率密度函数具体的形式，只要我们能得到X的期望和方差，则就可以通过X的数字特征来判断X的分布函数。

由混沌系统的有界性可知，混沌系统的混沌序列值必然会落在有限区间上；由上面的新系统分岔图可知，新系统产生的序列x(n)∈[0,1]。假设T(L-LSS)混沌序列是随机且均匀分布的，则其序列在区间中出现的概率应该是相同的，即x(n)为均匀分布。为了证明假设的正确性，下面通过新系统产生的混沌序列经过变换之后的序列x(n)来计算对应的期望和方差，以计算结果与理论值比较来判断其是否满足均匀分布的特点。

通过前面L-LSS系统的分岔图可以明显地看出x(n)∈[0,1]，此时，式(8)和式(9)中的b=1、a=0，代入计算序列x(n)的期望与方差理论值。依据L-LSS系统的表达式(5)迭代产生100 000个混沌序列，通过式(7)变换得到变换之后的混沌序列值x(n)，以此序列值求取期望与方差实际值，计算结果如表2所示。

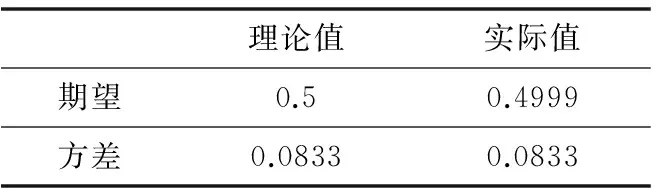
表2 序列x(n)期望与方差

由表2可以看出，新混沌系统产生的混沌序列通过变换以后所得序列x(n)的期望计算值与理论值相差很小，而且方差的计算值与假设其是均匀分布的理论值相等。以此就可以断定新的L-LSM混沌系统产生的混沌序列x(n)满足均匀分布的特点。

3.2 T(L-LSS)序列随机性检测

由新的一维L-LSS系统生成的序列变换后首先做二值化处理，就是把序列编成只有0和1的序列。如果二值序列满足随机均匀分布，则其具有以下特点：

(1) 序列中0和1出现的概率相等，即对于已确定的二值序列，序列中的0、1出现的次数应该相等；

(2) 状态转移的概率应该近似相等；

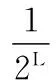
为了判断新T(L-LSS)混沌序列是否满足均匀分布的随机特性，产生80 000个混沌序列值，选择序列30 000到80 000之间的N=50 000个点，这是因为开始迭代的序列值有可能没有完全进入混沌状态。因此，跳过这些点，之后对这50 000个值做二值化处理，即进行0，1量化，量化完成之后，对量化后的序列x(n)进行频率检验、序列检验和游程检验。

频率检验就是统计二值化处理之后的序列中0和1出现的次数，观察其各自出现的次数是否相等。样本总数50 000个，如果满足均匀分布的特点，则序列x(n)中0和1的个数应该相等，即对应于50 000个样本，序列x(n)中就应该出现25 000个0和25 000个1。对序列x(n)进行统计得，0出现的次数N0=25 003，1出现的次数N1=24 997，并不等于25 000。在这种情况下，就需对样本出现的波动做假设检验，看其波动是不是在可接受的范围内。

由χ2分布表知：自由度1、显著水平0.05的χ2值为3.841。将N0、N1代入χ2分布检验公式中进行计算，完成假设检验：

(10)

所得χ2值为0.00072，远小于3.841，在其可信的区间内，因此可以认为序列x(n)通过了假设检验，即可认为序列x(n)中的0和1出现次数基本上是相等的。

=0.15816

(11)

其结果远小于5.9915，在其可信区间内，所以序列x(n)通过了假设检验，可被认为序列中的各态状态转移概率近似相等。

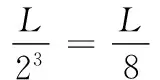
表3 游程检验

4 L-LSS混沌系统的应用

4.1 图像加密算法

为验证T(L-LSS)混沌伪随机序列的加密特性，以图像信息为研究基础，对于大小为M×N的灰度图像IM×N，通过下面描述的算法对IM×N图像进行加密和解密。

步骤1给定具体的初始参数，以L-LSS(式(5))混沌系统迭代产生一大小为M×N的矩阵CM×N；

(12)

其中floor为向下取整运算，mod为取模操作，EncM×N则为加密之后的图像。解密过程为加密的逆过程，这里不再赘述。

以512×512大小的Lena图为例，取密钥为u=2,u1=4,X0=0.2代入式(5)中获得混沌序列值，通过式(7)变换之后作为伪随机序列对图像进行加密。仿真结果如图6所示，明文图像与密文图像直方图分布如图7所示。由其直方图明显看出，密文图像变成了像素值均匀分布，明文的统计特性被完全打破，使明文的相关性大大降低。图8为正确解密与错误解密结果，正确解密时输入与加密时相同的密钥u=2,u1=4,X0=0.2进行解密操作，错误解密时对u参数做微小的改变，相差10-15进行解密，由结果可见密文对密钥具有很高的敏感性。

图6 明文图像与密文图像

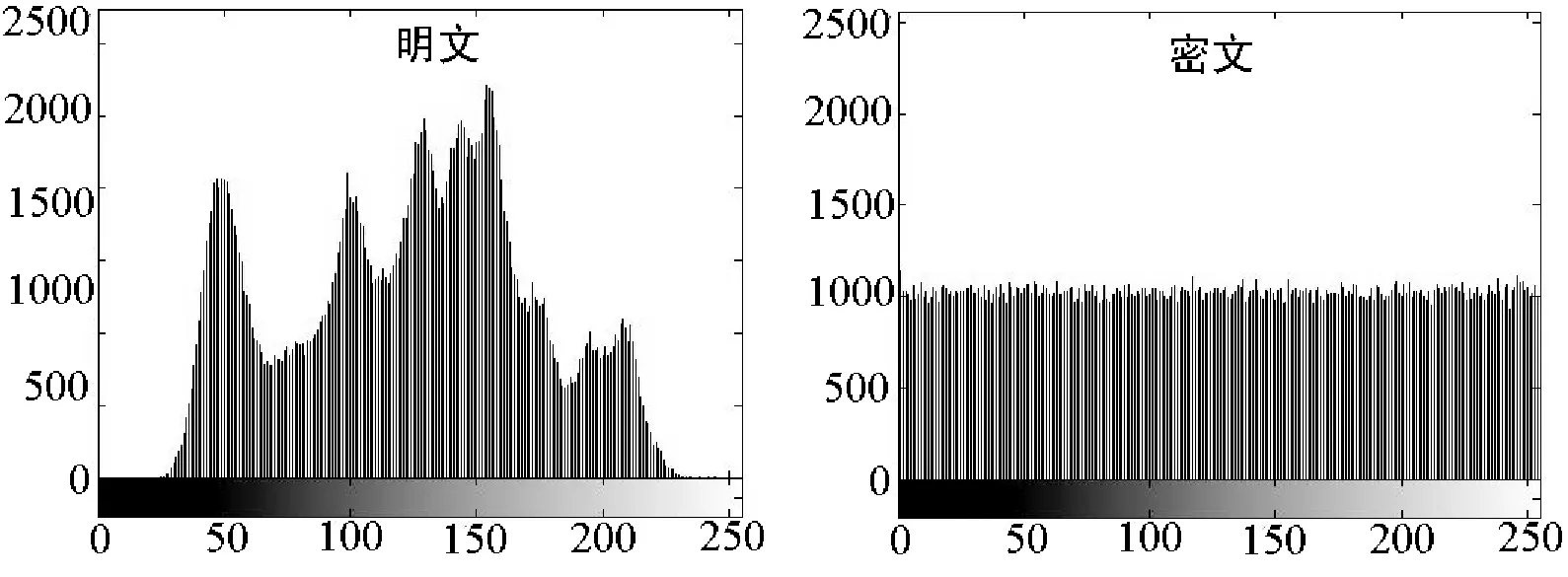
图7 明文图像直方图与密文图像直方图

图8 正确解密与错误解密结果

4.2 相关性分析

一个有意义的图像的明显特征就是数据的冗余特性，像素点与它临近像素点有很高的相关性。图像加密的目的就是要破坏原来图像的这种相关性，使加密后的图像变换为只有很小或者几乎没有相关性的似噪声图像。明文图像Lena.png与密文图像像素点分布如图9所示，可以很直观地看到，图像在加密之前具有很强的相关性，而加密之后没有明显的相关性。

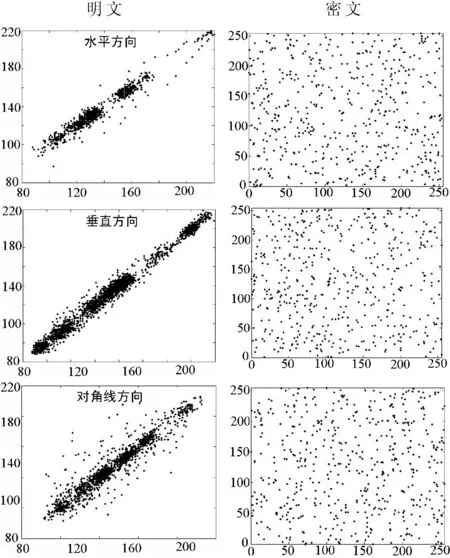
图9 不同方向相关性

为了更进一步对相关性研究，通过计算原始图像和加密之后的图像的相关性值，来验证加密的效果。相关性值如下公式给出：

(13)

具体的计算法如下：

(14)

其中：μ和σ是平均值和标准方差，E[·]表示的是求其期望值；Cxy∈(-1,1)，xi、yi是两个相邻的像素点的值。

一个好的加密图像是无法被识别的，相关性值Cxy≈0。以式(14)进行计算，得出结果如表4所示。

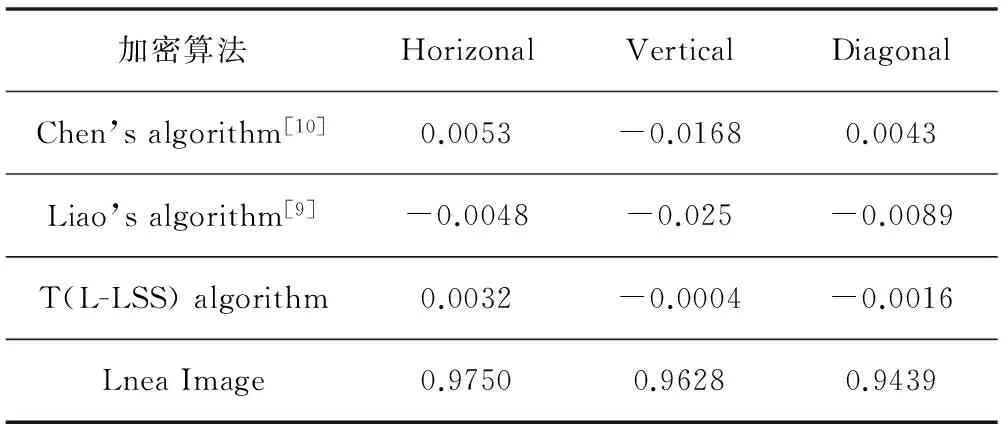
表4 相关性分析

4.3 信息熵分析

信息熵IFE被定义为评价一个随机变量的不确定性，由下面的等式定义：

(15)

其中F是灰度值，P(L=l)是像素值为l的百分比。

IFE可以用来评价一个图像的随机性，IFE的值越大就意味着图像拥有极强的随机性。对于灰度值属于[0,255]的灰度图像，IFE的理想最大值为8。表5给出了加密之前与加密之后图像的IFE的值，加密之后图像的IFE的值非常接近8。

表5 信息熵分析

由表5可以看出，尽管本文所设计的图像加密算法只是简单做了异或操作，但是加密效果却比文献[9]算法的加密效果好。由此可以得出结论，在设计混沌图像加密算法时，如果所采用的混沌系统产生的混沌序列随机性强且分布均匀，则可以获得更好的加密效果和更高的安全性，在相同加密性能指标下则可以降低算法的复杂性。

5 结 语

本文提出的构造一维混沌系统的方法具有很明显的效果，构造的新一维混沌系统具有更好的混沌特性。该方法可以改善混沌系统混沌区间不连续问题，同时也可以提高系统的Lyapunov指数。对构造的新混沌系统(L-LSS)混沌序列的分布不均匀进行了改善，改善效果明显。最后，基于改善之后的混沌序列对图像进行了加密测试，实验结果表明，基于T(L-LSS)伪随机混沌序列对初始参数具有极强的敏感性。可见T(L-LSS)混沌序列为满足均匀分布的伪随机序列，以此伪随机序列设计的混沌加密算法可以获得更高的安全性。文中提出的组合结构可以获得很多性能更好的新一维混沌系统，且实现灵活。

[1] Zhongyun Hua,Yicong Zhou,Chiman Pun,et al.2D Sine Logistic Modulation map for image encryption[J].Information Sciences,2015,297:80-94.

[2] Yicong Zhou,Long Bao,C L Philip Chen.A new 1D chaotic system for image encryption[J].Signal Processing,2014,97:172-182.

[3] 禹思敏.混纯系统与混纯电路—原理、设计及其在通信中的应用[M].西安:西安电子科技大学出版社,2011.

[4] Skrobek A.Cryptanalysis of chaotic stream cipher[J].Physics Letters A,2007,363(1-2):84-90.

[5] 王光义,袁方.级联混沌及其动力学特性研究[J].物理学报,2013,62(2):020506.

[6] Eckmann J P,Ruelle D.Ergodic theory of chaos and strange attrange attractors[J].Reviews of Modern Physics,1985,57(3):617-656.

[7] Wolf A,Swift J B,Swinney H L,et al.Determining Lyapunov exponents from a time series[J].Physica D:Nonlinear Phenomens,1985,16(3):285-317.

[8] 曹光辉,胡凯,佟维.基于Logistic均匀分布图像置乱方法[J].物理学报,2011,60(11):110508.

[9] Liao X F,Lai S Y,Zhou Q.A novel image encryption algorithm based on self-adaptive wave transmission[J].Signal Processing,2010,90(9):2714-2722.

[10] Chen G R,Mao Y B,Chui C K.A symmetric image encryption scheme based on 3D chaotic cat maps[J].Chaos,Solitons and Fractals,2004,21(3):749-761.

[11] 张晓强,王蒙蒙,朱贵良.图像加密算法研究新进展[J].计算机工程与科学,2012,34(5):1-6.

[12] Yicong Zhou,Long Bao,C L Philip Chen.Image encryption using a new parametric switching chaotic system[J].Signal Processing,2013,93(11):3039-3052.

[13] Radu Boriga,Ana Cristina Dăscălescu,Iustin Priescu.A new hyperchaotic map and its application in an image encryption scheme[J].Signal Processing:Image Communication,2014,29(8):887-901.

[14] 孙福艳,吕宗旺.空间混沌序列的加密特性研究[J].物理学报,2011,60(4):040503.

[15] Murillo-Escobar M A,Cruz-Hernández C,Abundiz-Pérez F,et al.A RGB image encryption algorithm based on total plain image characteristics and chaos[J].Signal Processing,2015,109:119-131.

[16] Wang Zhen,Huang Xia,Li Yuxia,et al.A new image encryption algorithm based on The fractional-order hyperchaotic Lorenz system[J].Chinese Physics B,2013,22(1):010504.

[17] 陈舒,韩太林.图像加密算法的发展现状[J].中国科技信息,2012(2):78,86.

[18] Xingyuan Wang,Na Wei,Doudou Zhang.A novel image encryption algorithm based on chaotic system and improved Gravity Model[J].Optics Communications,2015,338:209-217.

[19] 张永红,张博.基于Logistic混沌系统的图像加密算法研究[J].计算机应用研究,2015,32(6):1770-1773.

[20] 朱从旭,孙克辉.对一类超混沌图像加密算法的密码分析与改进[J].物理学报,2012,61(12):120503.

[21] Shevchenko I I.Lyapunov exponents in resonance multiplets[J].Physics Letters A,2014,378(1-2):34-42.

[22] Yue Wu,Yicong Zhou,Joseph P,et al.Design of image cipher using latin Squares[J].Information Sciences,2014,264:317-339.

[23] Yicong Zhou,Weijia Cao,C L Philip Chen.Image encryption using binary bitplane[J].Signal Processing,2014,100:197-207.

ON A NEW 1D CHAOTIC SYSTEM AND ITS ENCRYPTION CHARACTERISTIC

Li Juanxia1Sun Huiming2*Chen Wei2

1(School of Physics and Electromechanical Engineering,Hexi University,Zhangye 734000,Gansu,China)2(College of Electrical and Control Engineering,Xi’an University of Science and Technology,Xi’an 710054,Shaanxi,China)

This paper proposes a new composite structure for generating 1D chaotic system. Two new 1D chaotic systems are designed by using this structure. Through plotting Lyapunov exponent diagram and bifurcation diagram we studied the performance of two new chaotic systems, study results showed that the new 1D chaotic system generated by this structure had the advantages of large and continuous chaotic range, uniform chaotic sequence distribution, high system Lyapunov exponent and more controllable parameters, etc. In order to further improve the uniformity of chaotic sequence distribution, we designed a transformation process. After the transformation the chaotic sequence satisfied the uniform distribution. At last, in order to demonstrate its applications in information security, we designed a simple image encryption and decryption algorithm. The new systems were simulated and tested their performances on Matlab, results showed that after the transformation the chaotic sequence had higher encryption characteristic.

Chaos Image encryption Statistical analysis

2015-05-20。李娟霞，讲师，主研领域：机电控制，计算机测控系统，智能信息处理。孙会明，硕士生。陈薇，硕士生。

TP309.7

A

10.3969/j.issn.1000-386x.2016.11.073