一种基于多数字基整数的数字水印分存算法

钱言玉 吴友情

(合肥师范学院公共计算机教学部 安徽 合肥 230061)



一种基于多数字基整数的数字水印分存算法

钱言玉 吴友情

(合肥师范学院公共计算机教学部 安徽 合肥 230061)

针对一般水印算法功能单一，而现有水印分存算法中只能实现二进制水印图像分存的问题，将多数字基整数应用到数字水印分存技术中，提出一种灰度水印图像的分存方法。实验结果表明,该方法可以有效防止外部欺诈和内部欺诈，实现了在多个用户间的秘密共享，也可以应用于身份认证，且可以抵抗多种常用图像的处理攻击，具有一定的鲁棒性。

水印分存 多数字基整数 灰度水印 秘密共享 身份认证

0 引 言

在网络技术的发展下，国内外学者提出了很多数字水印算法，但是这些算法中能解决数字水印分存的问题的很少。因为在这些算法中只有一个密钥，任何人只要他拥有这个密钥，就可以重构数字水印，就会被默认为是作品的拥有者。如果多人协同合作拥有一个数字水印，可以运用某种方法设计出n份不同的子水印，分配给n位参与者。当获取其中的t(t0≤t≤n,t0是指定秘密共享方案固有的阈值)份子水印，共享的数字水印就可以被恢复；反之则无法恢复出共享的数字水印。这就是秘密共享的问题。

数字水印分存是在数字水印的基础上，将秘密共享[1-5]的思想用于数字水印技术中。姚惠明、牛少彰等人[6,7]提出的数字水印分存技术将分存后的子水印嵌入在LSB上，只能抵抗剪切攻击，不能抵抗其他类型攻击，健壮性差。基于矢量共享方案DCT域上的数字水印分存算法[8]提出在DCT变换域中嵌入分存子水印，这在一定程度上增强了子水印的健壮性，但对剪切和压缩之外的攻击效果仍很不理想。基于视觉的秘密共享方案[9]不需要复杂的密码机制和数学运算，可以由人眼直接解码，但这种方案在秘密共享的过程中容易产生噪声。基于图像的多用户共享的数字水印系统[10]，把秘密嵌入载体图像，没有产生明显的噪声，但仍只能实现二进制图像的秘密共享。

本文提出的基于多数字基整数的数字水印分存算法，可以实现灰度数字水印图像的共享[11]。多数字基整数[12]用来将灰度数字水印分裂成n个没有意义的子水印，分派给n个用户再分别嵌入到载体图像的不同区域。本算法可用来实现在多个用户间的秘密共享，也可以应用于身份认证[13,14]，且可以抵抗多种常用图像的处理攻击，具有一定的鲁棒性。

1 多数字基整数

定义1称整数dn-1dn-2…d0为单数字基整数，如果此整数的所有系数di(0≤i≤n-1)均以十进制数a为基底，其中di的取值为0到a-1的十进制整数。则dn-1dn-2…d0转化为十进制整数为：

dn-1dn-2…d0=d0+…+dn-2×an-2+

dn-1×an-1

(1)

定义2称整数dn-1dn-2…d0为多数字基整数，di为此整数的第i位系数，如果每位系数di以十进制常数bi>0(i=0,1,…,n-1)为基底，其中di的取值范围是0到bi-1的十进制整数。多数字基数dn-1dn-2…d0同样可以表示成dn-1(bn-1)dn-2(bn-2)…d2(b2)d1(b1)d0(b0)，它的十进制结果可以按如下公式进行计算：

dn-1(bn-1)dn-2(bn-2)…d2(b2)d1(b1)d0(b0)

=dn-1×(bn-2×bn-3×…×b0)+

dn-2×(bn-3×bn-4×…×b0)+…+

d2×(b1×b0)+d1×b0+d0

=((…((dn-1×bn-2+dn-2)×bn-3+dn-3)×

…+d2)×b1+d1)×b0+d0

(2)

定义3称以十进制常数bn-1bn-2…b0为基底，由定义2定义的多数字基整数的集合为多数字基整数系统。

性质1任何一个十进制整数都可以转化成一个多数字基整数dn-1(bn-1)dn-2(bn-2)…d0(b0)，其逆命题也真。

性质2一个n位的多数字基数dn-1(bn-1)dn-2(bn-2)…d0(b0)，可以表示m bit二值信息，如果其基底bn-1,bn-2,…,b0满足：

(3)

2 基于多数字基整数的数字水印分存算法

将灰度数字水印图像通过多数字基整数分成n(n≥2)份子水印后，需要将这些子水印嵌入到载体图像中，这里的水印嵌入与提取算法不限定，只要适合就行。本文采用在小波域上结合人眼视觉特性的灰度水印自适应嵌入与提取算法[15]，将数字水印分成2(n=2)份。分派给2(n=2)个用户再分别嵌入到载体图像的不同区域，基于多数字基整数的数字水印分存算法实现了灰度数字水印图像的分存，提高了水印的嵌入容量，且与以前的算法相比，具有更强的健壮性和鲁棒性。

2.1 灰度数字水印的分块

我们用多数字基整数将原始数字水印分成若干份，这里SI表示原始灰度水印，分开后的子水印用PI0,PI1,…,PIn-1表示，SI和PI0,PI1,…,PIn-1可以定义如下：

SI={s(i,j)|0≤s(i,j)≤255 0≤i,j≤N-1}

(4)

PIk={pk(i,j)|0≤pk(i,j)≤dk0≤i,j≤N-1}

(5)

PIk(k=0,1,…,n-1)的大小同SI，dk=bk-1，bk为对应用户所取的整数基底。若取两位基底为b1=18，b0=22，则整数200可以被如下系数表示d1=9，d0=2，即200=d1×b0+d0=9×22+2。

如图1所示，PIi(i=0,1)是原始数字水印SI分块后的2块子水印，它们是分别对应系数di(i=0,1)的矩阵。这样我们就可以将这些分块的矩阵，也就是子水印嵌入到载体图像的不同区域中。

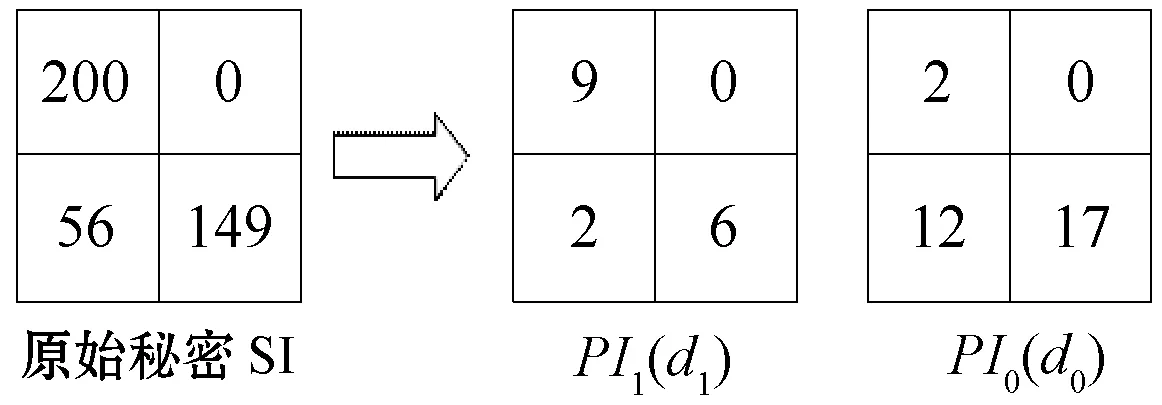
图1 多数字基整数的数字转换

2.2 子水印的嵌入与提取

本算法的流程如图2所示，其主要步骤如下：

步骤1为了增强安全性，在原始灰度数字水印图像分裂前，采用基于队列变换的数字图像置乱算法[16]对其进行置乱预处理。基于队列置乱变换有四个参数:s_key(Type,I,J,L),其中Type表示置乱变换类型，(I,J)表示置乱变换的参照点，L表示置乱变换迭代的次数。

步骤2用多数字基整数将置乱后的灰度数字水印图像分裂成n(n≥2)份子水印图像。相应的多数字基基底可以作为密钥，被对应的用户所拥有。

步骤3将各子水印图像嵌入载体图像的不同区域中。

步骤4提取各子水印图像，原始数字水印图像可以按照定义2进行恢复后再进行逆置乱获得。

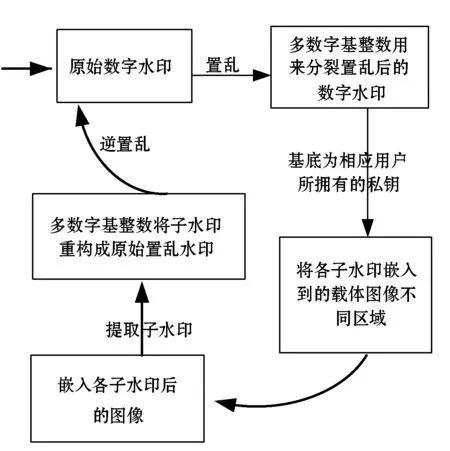
图2 基于多数字基整数的数字水印分存算法

3 实验结果与分析

为测试本文算法的有效性，在仿真实验中，水印采用256级的大小为64×64的灰度图像。为了提高水印的安全性和抗剪切攻击能力，采用队列变换的置乱算法先对原始水印进行预处理，再采用合适的基底将置乱后的数字水印表达为两组不同的多数字基整数，即两块子水印。这里的载体图像采用256级灰度，大小为512×512的“Lena”、“Goldhill”、“Camera”、“Airplane”和“Peppers”图像分别试验。限于篇幅，本文以Lena图像为代表，将其进行三级小波变换，两块子水印分别嵌入到对应的载体图像的低频域中和中频域中。原始水印、置乱后的水印如图3所示。

图3 原始水印和置乱水印

图4为原始载体图像，图5为嵌入2个子水印后的带水印图像，从视觉效果看，很难感觉到水印的存在，说明该水印算法具有较好的不可见性。

图4 原始载体图像

图5 嵌入两块子水印后的图像PSNR=34.5578

3.1 鲁棒性与安全性分析

为验证基于多数字基整数的数字水印分存算法的抵抗攻击能力，实验中对嵌入水印后的图像进行一些处理，然后提取子水印。归一化互相关系数NC来判断提取水印的鲁棒性，用来定量评价提取水印Wextract与原始水印W两者之间的相似度[15]。

(4)

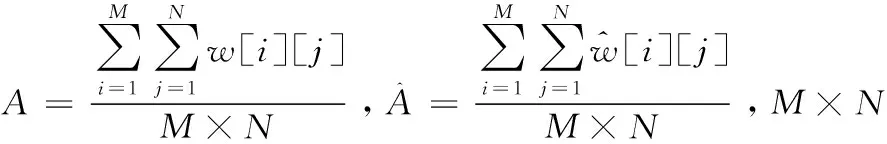
如表1所示，“子水印1+子水印2”表示两个子水印都被提取，“子水印1”表示只有第一块子水印被提取，第二块子水印的密钥未知。“子水印2” 表示只有第二块子水印被提取，第一块子水印的密钥未知。为了分析基于多数字基整数的数字水印分存算法的安全性，我们从外部欺诈和内部欺诈两个方面来考虑：就外部欺诈而言，敌手很难获得2份子水印，再完成逆置乱，从而恢复原始数字水印；就内部欺诈来说，内部子水印合法拥有者在不知道其他子水印的情况下，即使提取出了自己的子水印，也变得毫无价值。所以本文提出的数字水印分存算法，不仅能防止外部欺诈，也能防止内部欺诈，达到了秘密共享的目的。

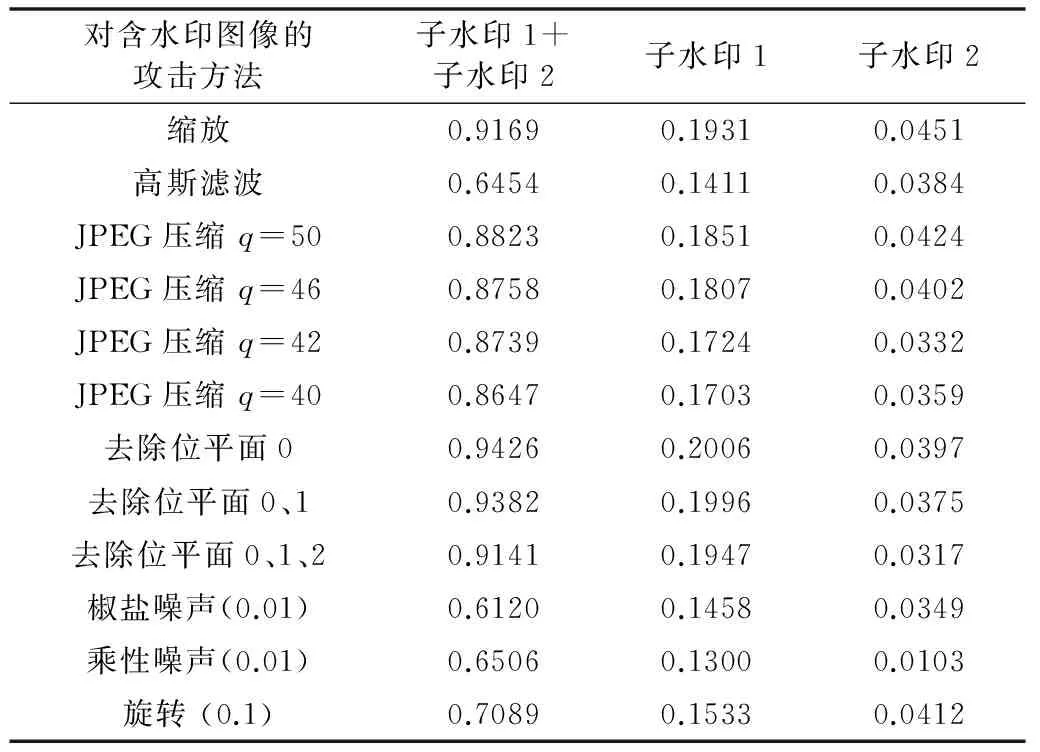
表1 水印抗攻击实验结果

3.2 实验结果比较及分析

运用数字水印技术来分享一个秘密，同种类型的算法并不多。一般说来，不容易在这类算法中来比较彼此性能的优劣，因为它们使用不同的规则用不同的方法来达到秘密共享的目的。在表2中我们列出了几条一般性能的比较。

表2 与相关系统的性能比较

对于数字水印系统，像不可见性和鲁棒性是考虑的重点，但秘密共享能力一般并不考虑。视觉密码学主要考虑的是秘密共享能力，为了达到这个目的，恢复出的秘密的质量欠考虑，恢复的效果往往也不理想。基于多数字基整数的数字水印分存算法能实现秘密的共享，同时能克服上述缺陷。表2中“○”表示“重要”或“拥有”，“×”表示“不考虑”或“不重要”。

4 结 语

数字水印分存是将秘密共享的思想引入数字水印技术中，秘密共享在重要信息和秘密数据的安全保存、传输及合法利用中起着关键的作用。共享方案在使用的时候，一方面可以防止外部欺诈获得秘密；另一方面可以防止内部欺诈，内部子秘密合法拥有者在不知道其他分存水印的情况下，即使提取出了自己的分存水印，也变得毫无价值。这在现实中是非常有意义的，可以防备子秘密合法拥有者盗窃秘密。本文提出了一种能简单有效实现灰度数字水印图像分存的算法，利用多数字基整数将原始数字水印分裂成多个子水印，当且仅当获得t(t0≤t≤n,t0为阈值)份子水印时(本文中t=2,t0=2)，原始数字水印才可以恢复。实验表明，基于多数字基整数的数字水印分存算法能有效抵抗外部欺诈和内部欺诈，同时实验结果表明，该算法具有很强的鲁棒性和不可见性，实现了灰度数字水印图像的多用户共享。

[1] 刘海，彭长根，田有亮，等.(2,2)贝叶斯理性秘密共享方案[J].电子学报,2014,42(12):2481-2488.

[2] Zhang Zhifang,Liu Mulan.Rational secret sharing as extensive game[J].Scinece China Information Sciences,2013,56(3):1-13.

[3] 沈刚，郁滨.基于异或的(k，n)多秘密视觉密码[J].小型微型计算机系统,2013,34(9):2116-2119.

[4] Harn L,Fuyou M,Chang C C.Verifiable secret sharing based on the Chinese remainder theorem[J].Security and Communication Networks,2014,7(6):950-957.

[5] 蓝才会，王彩芬.一个新的基于秘密共享的条件代理重加密方案[J].计算机学报,2013,36(4):895-902.

[6] 姚惠明，隋爱芬，牛少彰，等.基于矢量共享方案的数字水印分存算法[J].电子与信息学报,2003,25(12): 1612-1616.

[7] 牛少彰，钮心忻，杨义先，等.基于拉格朗日插值公式的数字水印分存算法[J].北京邮电大学学报,2003,26(3):8-11.

[8] 姚惠明，周冠玲，杨义先，等.一种基于矢量共享方案的DCT域上数字水印分存算法[J].计算机学报,2004,27(7):998-1003.

[9] Fuhgwo Jeng,Kaisiang Lin,Chihhung Lin,et al.Visual multi-secret sharing with friendliness [J].Journal of Shanghai Jiaotong University (Science),2014,19(4):455-465.

[10] Wang F H,Yen K K,Jain L C,et al. Multiuser-based shadow watermark extraction system [J].Information Sciences,2007,177(12): 2522-2532.

[11] 罗斌，吴友情，吕皖丽，等.一种基于相位相关拼接的数字水印分存算法[J].中国科技论文,2009,4 (2):103-108.

[12] Wu D C,Tsai W H.Data hiding in images via multiple-based number conversion and lossy compression [J].IEEE Transactions on Consumer Electronics,1998,44(4): 1406-1412.

[13] 周晓斌，许勇，张凌.一种开放式PKI身份认证模型的研究[J].国防科技大学学报,2013,35(1):169-174.

[14] 刘云芳，左为平.基于身份无可信中心的指定验证人代理多重签名方案[J].计算机应用与软件,2013,30(4):316-318.

[15] 向德生，熊岳山，朱更明.基于视觉特性的灰度水印自适应嵌入与提取算法[J].中国图象图形学报,2006,11(7):1026-1035.

[16] 李敏，费耀平.基于队列变换的数字图像置乱算法[J].计算机工程,2005，31(1):148-152.

A WATERMARKING SHARING SCHEME BASED ON MULTIPLE-BASED NUMBER

Qian Yanyu Wu Youqing

(Department of Public Computer Teaching,Hefei Normal University，Hefei 230061, Anhui, China)

Aiming at the problems that general watermarking algorithms only have single function,while existing watermark sharing algorithms can only realise binary watermark image sharing,we proposed a gray-level watermarking image sharing scheme,which applies the multiple-based number to digital watermarking sharing technology.Experimental results showed that the proposed scheme can effectively prevent external and internal frauds,and achieve the secret sharing among multiple users,it can be also applied to authentication,can resist a couple of processing attacks on common images,and has certain robustness.

Watermarking sharing Multiple-based number Gray-scale watermark Secret sharing Identity authentication

2015-07-18。钱言玉，实验师，主研领域：信息安全。吴友情，讲师。

TP391.41

A

10.3969/j.issn.1000-386x.2016.11.072