基于水印主成分的小波域数字水印方法

肖振久 李 南 王永滨 姜正涛 陈 虹

1(辽宁工程技术大学软件学院 辽宁 葫芦岛 125105)2(中国传媒大学计算机学院 北京 100024)



基于水印主成分的小波域数字水印方法

肖振久1,2李 南1王永滨2姜正涛2陈 虹1

1(辽宁工程技术大学软件学院 辽宁 葫芦岛 125105)2(中国传媒大学计算机学院 北京 100024)

针对一类奇异值分解水印算法中存在严重的虚警错误、鲁棒性和透明性难以平衡的问题，提出一种基于水印主成分的小波域数字水印新思路。该方法首先将三级离散小波变换(DWT)作用于原始载体图像，再对三级逼近子图LL3运用奇异值分解(SVD)，选择水印图像左奇异矩阵和奇异值矩阵的乘积作为水印主成分，最后借鉴果蝇优化算法(FOA)确定最优的水印嵌入系数，嵌入水印图像的主成分。实验结果表明，与传统的SVD图像水印算法相比，该方法在消除虚警问题的同时，也可使水印的鲁棒性和透明性达到最佳平衡。

奇异值分解 水印主成分 虚警错误 果蝇优化算法 鲁棒性 透明性

0 引 言

互联网和多媒体技术的飞速发展为数据传输开辟了新途径，越来越多的数字作品(文字，声音和图像)在网络上迅速传播[1,2]。然而实现数据共享的同时也产生了一系列问题，如数字作品的非法盗用，篡改及仿冒，如何才能有效地确保数字媒体的安全性和原始图像的真实性。在众多版权保护的手段中，尤其是一类奇异值的数字水印方案已经得到广泛关注。

由于图像奇异值分解后的奇异值对各种攻击具有一定的抵抗能力，一部分学者提出了基于SVD的水印方法。刘瑞桢等[3]于2001年将奇异值分解理论首次应用于数字水印系统中，该方法将水印图像嵌入到载体图像的奇异值中。随后文献[4,5]提出一种将SVD和DWT相结合的水印算。文献[6]提出一种DWT-SVD和FA相结合的优化数字水印算法。借鉴FA算法来确定水印的嵌入强度。从以上文献得出基于图像奇异值分解的数字水印算法大致分为两类，一类是将水印图像嵌入到载体图像的奇异值中，另一类是将水印图像的奇异值嵌入到载体图像的奇异值中。虽然这两类水印算法都取得了较好的效果，但是这两类算法在水印提取阶段存在严重的虚警错误。根本原因为水印提取过程都要用到原始图像奇异值分解后的正交矩阵U和V，而正交矩阵U和V几乎包含了图像的全部结构信息。在水印提取阶段，如果恶意提取者利用伪造图像奇异值分解后的正交矩阵来重构水印，则可以重构出任意期望的水印图像。事实上该伪造图像并没有嵌入到载体图像，故该类算法在实现版权保护方面还存在一定的缺陷。

针对虚警错误，文献[7]将SVD分解的正交矩阵 U 作为控制参数。在水印提取阶段，当U参量的相似程度大于给定阈值时，则进行水印提取。通过大部分攻击实验发现，攻击后提取出的U相似度都大于给定阈值，没能从根本上解决虚警错误问题。文献[8]提出了一种量化的SVD水印算法。虽然该算法具有较好的鲁棒性，但该算法在水印嵌入过程中回避植入水印信息。文献[9]提出了一种改进的DWT-SVD域参考水印方案。该方案虽然解决了虚警问题，但鲁棒性相对较差，实用价值不高。

本文提出了一种基于水印主成分[10-13]的小波域数字水印算法，从本质上解决了水印的虚警问题。同时借鉴文献[6]的思想，利用新兴果蝇优化算法全局寻优的特点，搜寻最佳的水印嵌入系数，使水印的鲁棒性和透明性达到综合优化。

1 相关理论基础

1.1 奇异值分解

对于矩阵对角化，奇异值分解作为一种有效的数值分析工具，在图像处理领域得到广泛应用。对于大小为m×n的数字图像A进行奇异值分解，则存在正交矩阵Um×m、Vn×n和对角矩阵Sm×n使得下式成立：

(1)

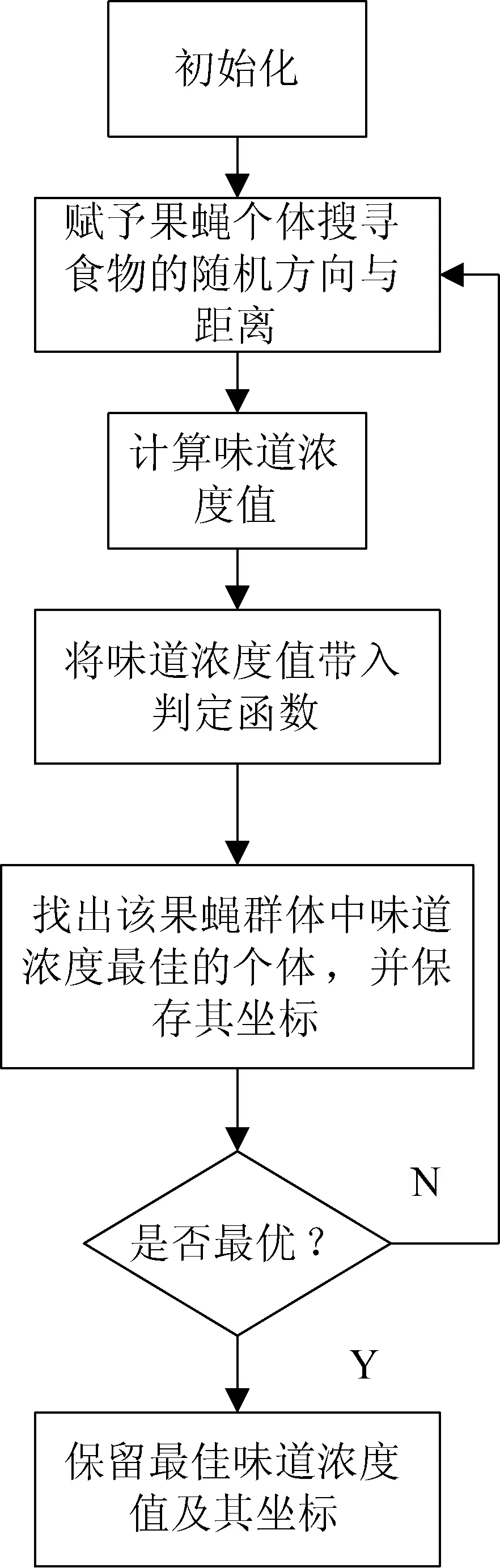
图1 果蝇优化算法流程图

其中U和V是正交矩阵，而S=diag(λi)是一个非对角上的值都是0的矩阵，其对角线上的元素值λi(i=1,2,…,r)且λ1≥…≥λr>0。列矩阵ui是矩阵U的左奇异矩阵，列矩阵vi是矩阵V的右奇异矩阵。

1.2 果蝇算法

果蝇优化算法是一种新兴的启发式群智能算法，它是从果蝇搜寻食物过程中演化出的一种全局优化的新思路[14-16]。果蝇不同于其他物种，它具有敏锐的视觉和灵敏的嗅觉，即使在40 km之外也能很好地搜寻空气中飘浮的各种味道，然后利用视觉系统发现食物和其他果蝇所处的位置，并往该方向飞去。该算法与其他智能算法相比，参数少，易于实现，广泛应用于科学和工程领域。其算法的具体流程如图1所示。

2 基于水印主成分的小波域数字水印算法描述

2.1 水印的预处理——Arnold变换

Arnold变换是数学家Vladimir I.Arnold在遍历理论中提出的一种变换，又称猫脸变换[17,18]。该变换通过改变图像像素点之间的位置关系来减少像素之间的关联程度，增加水印的安全性和鲁棒性，达到加密的效果。

本实验采用带有“辽宁工大”字样的二值图像，图像大小为64×64，置乱周期为48，图2是该图像部分Arnold置乱结果，n为置乱次数。

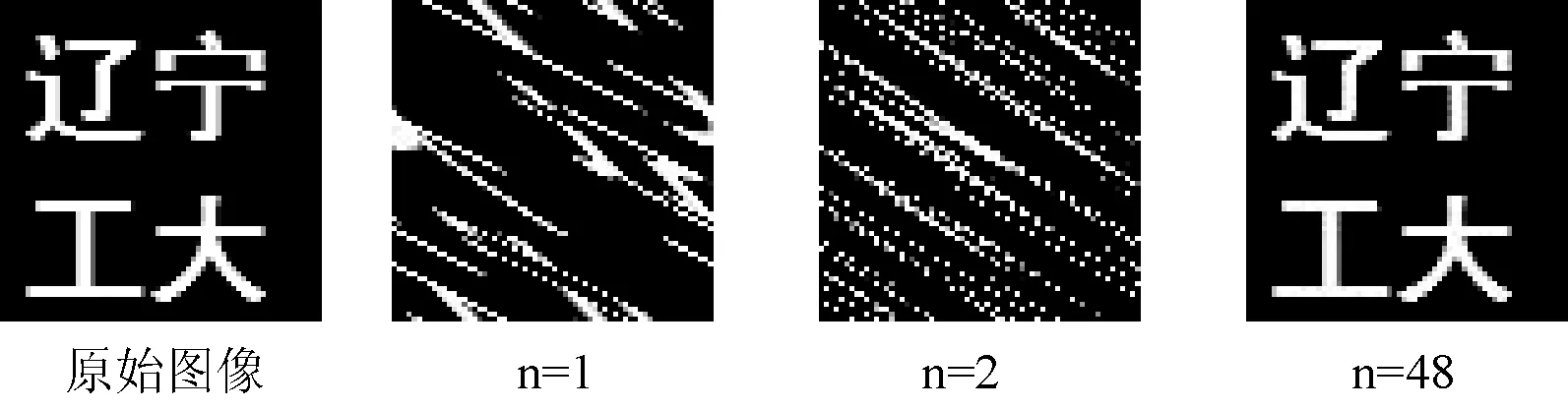
图2 Arnold变换不同迭代次数下的置乱图像

2.2 水印的主成分

为了从根源上解决该类水印算法存在的虚警错误，本算法选择左奇异矩阵U和奇异值矩阵S的乘积作为水印的主成分嵌入到载体图像，而在水印提取时只用到了右奇异矩阵。设置乱后的水印图像为W，按照下式即可得到水印的主成分。

W(i,j)=Uw(i,j)Sw(i,j)Vw(i,j)T

(2)

PCw(i,j)=Uw(i,j)Sw(i,j)

(3)

2.3 水印的嵌入

(1) 将原始载体图像I进行三级离散小波分解，取三级低频子带LL3进行SVD分解，取奇异值S作为水印的嵌入位置。

[U,S,V]=SVD(LL3)

(4)

(2) 按下面公式，将水印的主成分PCw嵌入到LL3子带的奇异值中。

S′=S+λ×PCw

(5)

其中λ为水印的嵌入强度。本方法中利用果蝇优化算法来搜索λ作为最佳嵌入阈值，达到鲁棒性和透明性整体优化的效果。

(3) 利用下式得到嵌入水印后的LL3子带。

LL3′=US′VT

(6)

(4) 将小波逆变换作用于嵌入水印后的三级子图，得到嵌入水印的图像

水印嵌入过程中的部分核心代码如下：

[cA1,cH1,cV1,cD1]=dwt2(I,′haar′);

% I为载体图像

[cA2,cH2,cV2,cD2]=dwt2(cA1,′haar′);

[cA3,cH3,cV3,cD3]=dwt2(cA2,′haar′);

[mm1,nn1]=size(cA3);

[U,S,V]=svd(cA3);

[Uw,Sw,Vw]=svd(double(w1));

%w1为置乱后的水印图像

PCw=Uw*Sw;

%构造水印主成分PCw

Temp=S+λ*PCw;

%嵌入水印主成分，λ为嵌入强度

CWI=U*Temp*V';

cA3=CWI;

X3=idwt2(cA3,cH3,cV3,cD3,′haar′);

%重构图像

X2=idwt2(X3,cH2,cV2,cD2,′haar′);

watermarked=idwt2(X2,cH1,cV1,cD1,′haar′);

2.4 水印的提取

(1) 对嵌入水印后的图像进行三级离散小波变换得到三级低频子带LL3*。

(2) 利用下面公式,提取置乱后的水印主成分。

(7)

(3) 利用水印的右奇异矩阵可以得到置乱的水印。

(8)

(4) 通过Arnold逆变换可得到原始的水印图像。

水印提取过程中部分核心代码如下：

[ccA1,ccH1,ccV1,ccD1]=dwt2(watermarked,′haar′);

[ccA2,ccH2,ccV2,ccD2]=dwt2(ccA1,′haar′);

[ccA3,ccH3,ccV3,ccD3]=dwt2(ccA2,′haar′);

WNN=zeros(mm1,nn1);

WN=zeros(mm1,nn1);

WN=(U'*(ccA3-cA3)*V)/λ;

%提取水印主成分

WNN=WN*Vw';

%提取水印

2.5 果蝇优化算法寻找最优的比例因子

本文利用果蝇优化算法来搜索水印嵌入时的最佳比例因子，将水印嵌入过程看作是一个最优化问题。在这个优化问题中，要兼顾水印的透明性和鲁棒性。将峰值信噪比(PSNR)和归一化相关系数(NC)作为本算法中透明性和鲁棒性的量化标准。通过FOA全局寻优的特点搜寻水印嵌入时的比例因子，使得水印的透明性和鲁棒性得到较好的平衡。同时算法根据目标的相对重要程度进行加权，得到适应度函数[6,19,20]。

(9)

其中，α、β∈(0,1)表示其相应的权值，满足α+β=1；N为水印攻击的次数；NCi为受到第i次攻击时提取到水印的相关系数；PSNR为得到水印时峰值性噪比；PSNRtarget为期望的PSNR；期望值偏低可以更好地提高水印的鲁棒性，反之，期望值过高可以提高水印的透明性，但鲁棒性较差。

3 仿真实验结果及分析

实验采用Matlab R2012b平台，载体图像选取512×512的Lena灰度图像，二值图像“辽宁工大”作为水印图像，大小为64×64，如图3(a)、(b)。果蝇优化算法中种群大小设定为20，迭代次数设定为100，适应度函数中的PSNRtarget设定为44，α=0.3,β=0.7。DWT采用haar小波函数将原始载体图像经过3次小波变换后，将水印信号的主成分嵌入到载体图像低频子带LL3的奇异值中，嵌入水印后的图像如图3(c)，提取出的水印图像如图3(d)所示。

图3 原始载体图像与水印图像

为了验证本算法可以有效地解决虚警问题，与文献[3-6]算法进行对比。选取图3(a)为载体图像，图3(b)为水印图像，伪造的水印图像如图4(a)，它们的大小依各自算法不同而不同，具体详见文献[3-6]。图4(b)-图4(e)分别是按文献[3-6]算法利用图4(a)生成的两个正交矩阵从嵌入水印图像中提取的水印；图4(f)是利用本算法从嵌入水印图像提取的水印。实验结果表明， 文献[3-6]提取出的水印和伪造的水印极为相似，存在严重的虚警问题，而本算法克服了该问题。

图4 本文算法与文献[3-6]实验结果比较

为了客观评价该算法的性能，采用峰值信噪比(PSNR)来衡量载体图像与原始图像之间的质量差异，采用归一化相关系数(NC)来描述提取水印与原水印的近似程度。

峰值信噪比(PSNR)定义:

(10)

归一化相关函数(NC)定义:

(11)

PSNR的值越大说明对载体图像的破坏越小，经测试，本文算法PSNR值为47.0983，人们已经无法用肉眼辨别水印的存在，故本算法具有良好的不可见性。

为了检验算法的鲁棒性，对嵌入水印后的图像进行常规攻击，分别为JPEG压缩、滤波、加噪、旋转和剪切攻击，然后提取水印图像，提取的水印图像如下所示。

(1) JPEG压缩

对图3(c)使用不同质量因子(30%、70%)的JPEG压缩攻击测试，实验结果如图5所示。

图5 JPEG压缩后的图像和提取的水印图像

(2) 滤波

对含水印的图像3(c)分别进行强度为3×3和5×5的中值滤波攻击和高斯滤波攻击，实验结果如图6所示。

图6 滤波攻击后的图像和提取的水印图像

(3) 加噪

对嵌入水印后的图像3(c)加入高斯噪声(均值为0、方差为0.01)和椒盐噪声(强度为0.01)，实验结果如图7所示。

图7 噪声攻击后的图像和提取的水印图像

(4) 剪切和旋转

对含水印图像3(c)分别进行剪切攻击(剪切图像左上角1/4)和旋转攻击(向左旋转10°)，实验结果如图8所示。

图8 剪切和旋转攻击后的图像和提取出的水印图像

为了更好地检测本文方法的性能，选择图3(a)为载体图像，图3(b)为水印图像，与文献[7,9]进行比较。从表1可以看出，本算法的综合抗攻击能力要明显优于文献[7]和文献[9]，尤其对剪切和旋转攻击有较强的鲁棒性。故本算法在解决了水印虚警错误的同时，极大限度实现了水印鲁棒性和透明性之间的平衡。

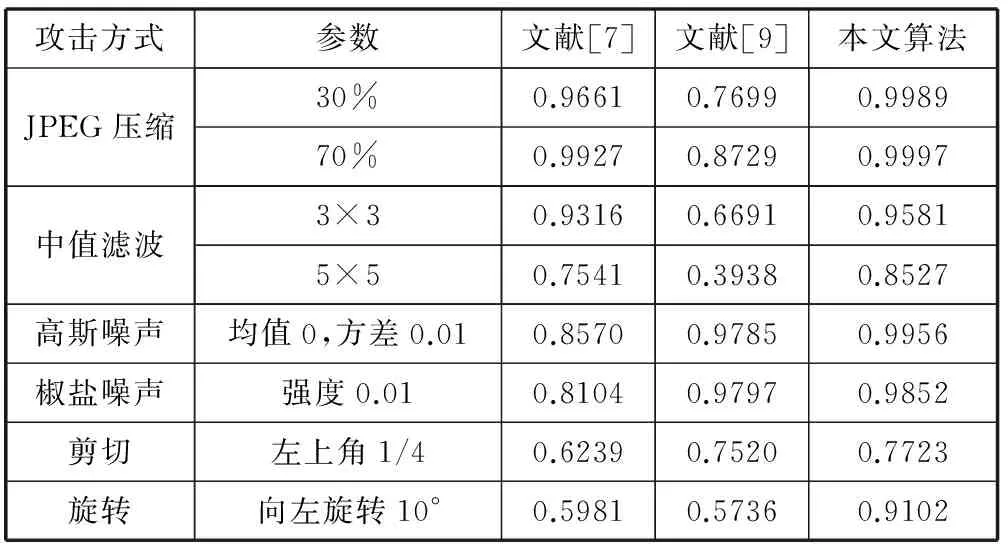
表1 本文方法与文献[7-9]相关系数对比

4 结 语

本文提出了一种将水印主成分和果蝇优化算法相结合的小波域数字水印方法。水印主成分可以有效地避免水印算法中存在的虚警问题，实现真正意义上的版权保护。而果蝇优化算法利用其全局寻优的特点，搜寻嵌入水印的最优比例因子，解决了水印鲁棒性和透明性难以平衡的矛盾。通过一系列实验证明该算法不仅解决了SVD水印算法的虚警问题，而且对滤波、噪声以及压缩等攻击具有较强的抵抗能力。

[1] 陈明奇,钮心忻,杨义先.数字水印的研究进展和应用[J].通信学报,2001,22(5):71-79.

[2] 易开祥,石教英,孙鑫.数字水印技术研究进展[J].中国图象图形学报,2001,6(2):11-17.

[3] 刘瑞祯,谭铁牛.基于奇异值分解的数字图像水印方法[J].电子学报,2001,6(2):168-171.

[4] 陈宏,宁静.SVD和DWT数字水印算法的应用研究[J].计算机仿真,2011,28(4):295-298.

[5] 张秋余,李凯,袁占亭.基于混沌和SVD-DWT的稳健数字图像水印算法[J]. 计算机应用,2010,27(2):718-720.

[6] Anurag Mishra,Charu Aqarwal,Arpita Sharma,et al.Optimized gray-scale image watermarking using DWT-SVD and Firefly Algorithm[J].Expert Systems with Applications,2014,41(17):7858-7867.

[7] 钱华明,于鸿越.基于SVD-DWT域数字图像水印算法[J].计算机仿真,2009,26(8):104-107.

[8] 蒋天发,熊祥光,蒋巍.一类SVD域水印问题分析及改进算法[J].计算机科学,2011,38(10A):62-65.

[9] 熊祥光,王力.一种改进的DWT-SVD域参考水印方案[J].计算机工程与应用,2014,50(7):75-79.

[10] RayShine Run,ShiJinn Horng,JuiLin Lai,et al.An improved SVD-based watermarking technique for copyright protection[J].Expert Systems with Applications,2012,39(1):673-689.

[11] JingMing Guo,Heri Prasetyo.False-positive-free SVD-based image watermarking[J].Journal of Visual Communication and Image Representation,2014,25(5):1149-1163.

[12] Punit Pandey,Shishir Kumar,Satish K Singh.Rightful ownership through image adaptive DWT-SVD watermarking algorithm and perceptual tweaking[J].Multimedia Tools and Applications,2014,72:723-748.

[13] Musrrat Al,Chang Wook Ahn.Comment on“Optimized gray-scale image watermarking using DWT-SVD and Firefly Algorithm”[J].Expert Systems with Applications,2015,42(5):2392-2394.

[14] Pan Wentsao.A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge-based Systems,2012,26(7):69-74.

[15] 韩俊英,刘成忠.自适应变异的果蝇优化算法[J].计算机应用研究,2013,30(9):2641-2644.

[16] 杨书佺,舒勤,何川.改进的果蝇算法及其在PPI网络中的应用[J].计算机应用与软件,2014,31(12):291-294.

[17] 吴成茂.离散Arnold变换改进及其在图像置乱加密中的应用[J].物理学报,2014,63(9):91-110.

[18] 张春森,范金健,胡平波.小波变换和Arnold变换的数字水印技术[J].西安科技大学学报,2012,32(1):95-100.

[19] Papakostas G A,Tsougenis E D,Koulouriotis D E.Moment-based local image watermarking via genetic optimization[J].Applied Mathematics and Computation,2014,227(11):222-236.

[20] 曾晴,马苗,周涛,等.基于布谷鸟搜索算法的小波域数字水印方法[J].小型微型计算机系统,2014,35(5):1155-1159.

WAVELET DOMAIN DIGITAL WATERMARKING METHOD BASED ON WATERMARK PRINCIPAL COMPONENTS

Xiao Zhenjiu1,2Li Nan1Wang Yongbin2Jiang Zhengtao2Chen Hong1

1(College of Software,Liaoning Technical University,Huludao 125105,Liaoning,China)2(School of Computer,Communication University of China,Beijing 100024,China)

For the problems of severe false positive error and being difficult to balance robustness and transparency in a kind of watermark algorithm with singular value decomposition (SVD), we proposed a new idea of watermark principal components-based wavelet domain digital watermarking method. The method first acts three-level discrete wavelet transform (DWT) on original carrier image, then applies SVD on three-level approaching subgraph LL3, and selects the product of left singular matrix and singular value matrix of watermark image as the principal components of watermark, finally it determines the optimal watermark embedding coefficient by learning from fruit fly optimisation algorithm (FOA), and embeds the principal components of watermark image. Experimental results showed that this method can achieve the best balance in robustness and transparency of the watermark while eliminating false-positive problem compared with traditional SVD image watermarking algorithm.

Singular value decomposition Principal components of watermark False positive error Fruit fly optimisation algorithm Robustness Transparency

2015-09-07。国家自然科学基金项目(61103199)；国家高技术研究发展计划项目(2011AA01A107-0)；教育部-中移动科研基金项目(MCM20130411)。肖振久，博士生，主研领域：网络与信息安全，数字版权管理。李南，硕士生。王永滨，教授。姜正涛，副教授。陈虹，副教授。

TP391

A

10.3969/j.issn.1000-386x.2016.11.063