自动属性加权的K-调和均值聚类算法
2016-12-26范桂明张桂珠
范桂明 张桂珠
(江南大学物联网工程学院 江苏 无锡 214122)
自动属性加权的K-调和均值聚类算法
范桂明 张桂珠
(江南大学物联网工程学院 江苏 无锡 214122)
针对K-调和均值算法中距离度量将所有属性视为相等重要而存在的不足,提出一种利用自动属性加权的改进聚类算法。在算法的目标函数中,用加权欧氏距离替代传统的欧氏距离,并证明了使得算法能够收敛的属性权重更新机制。为进一步提高聚类性能,将粒子群算法融入到改进的属性加权聚类算法中以抑制其陷于局部最优,其中采用聚类中心和属性权重的值同时表示粒子的位置进行寻优。在UCI数据集的测试结果表明,该算法的聚类指标平均提高了约9个百分点,具有更高的聚类准确性和稳定性。
K-调和均值 聚类 属性加权 粒子群
0 引 言
聚类分析是一种广泛使用的数据分析方法,一直被应用于多个领域,特别是在机器学习、数据挖掘、模式识别、图像处理等领域应用十分广泛。在所有的聚类分析算法中,K-means是最经典且使用最为广泛的一种算法,它是基于划分的原理,且算法过程简单快捷,容易实现。但是K-means算法也有两个主要的缺陷,对初始聚类中心的敏感以及容易陷入局部最优解。因此,针对上述缺陷很多文献不断提出改进方法,由Zhang[1]提出的K-调和均值KHM(K-harmonic means)算法能够有效解决对初始值敏感的问题。
由于KHM与K-均值仍然具有陷入局部最优的问题,一些启发式进化算法被用于与其组合而获得新的混合算法,以充分利用其全局搜索能力,现已成为对KHM的研究工作中最常用的方法。目前,融合粒子群算法PSO的PSOKHM[2]是较为经典的混合算法。随后,结合蚁群优化算法[3]、变邻域搜索算法[4]以及其改进版本[5]、候选组搜索算法[6]、帝国主义竞争算法[7]等相继被提出,然而它们并未直接与PSOKHM进行对比,并依据相应的实验结果可将它们看作为相近的研究工作。近来,由Bouyer等[8]提出一种结合改进PSO的混合算法KHM-MPSO能够获得比PSOKHM更准确且更具鲁棒性的聚类结果,其中利用了布谷鸟搜索算法的levy飞行策略进一步提高全局搜索能力。然而,这些混合聚类算法结合启发式算法进行搜索的策略均增加了时间复杂度,从而影响了计算效率,在这方面的改进值得进一步研究。此外,一些学者将模糊策略引入到KHM进行改进,使其具有软划分性能,如基于模糊KHM的谱聚类算法[9]以及其在单词-文档中的应用[10]。近来,Wu等[11]利用概率C均值的原理提出一种新颖的混合模糊K调和均值HFKHM(hybrid fuzzy K-harmonic means)聚类算法,能够有效解决对噪声敏感的问题。在上述的各种KHM算法中,均将数据的所有属性看作相等的作用进行距离度量,具有一定的局限性。由Huang等[12]提出一种自动变量加权型的W-k-means算法,它能够在聚类过程中度量不同属性的重要性,从而自动调整其权重使得更重要的属性具有相对较大的权重值。目前,基于属性加权的聚类算法已得到十分广泛的关注,被用于对各种算法进行改进[13-17],而尚未有关结合KHM的相关研究。
本文中首次将属性权重引入到KHM算法的距离度量中提出一种加权K-调和均值聚类算法WKHM(weight K-harmonic means),考虑不同属性对聚类的影响,并且在算法迭代过程中自动更新其权重。此外,为了进行更全面的分析,将WKHM与PSO相结合获得混合加权聚类算法PSOWKHM,并且与PSOKHM不同的是其将属性权重与类中心坐标相结合来表示每个粒子群个体。实验结果表明,本文算法能够有效提高聚类精度,具有较高的稳定性。
1 算法基本原理
1.1 K-调和均值聚类及其改进算法
K-调和均值算法的原理基本上与K均值是相似的,不同的是其使用调和均值HM(harmonic means)代替算术均值来计算目标函数。由于HM具有最小化群体内的偏差以及最大化群体间的偏差的特性,因此KHM能够有效克服对初始中心点敏感的问题。若数据集X=(x1,…,x2,…,xn),xi=(x1i,…,xqi)为空间Rq上的N个数据,将其划分为k个聚类簇,且每个聚类的中心用cj表示。根据文献,K-调和均值的目标函数为[1]:
(1)
这里采用欧氏距离计算数据xi到聚类中心的cj的距离,即dij=‖xi-cj‖,p是一个输入参数,对算法的性能具有重要的影响,研究发现当p≥2时聚类的效果比较好[1]。聚类过程通过迭代使得目标函数值不断减小并保持稳定,直至结束运行。每次迭代中,各个聚类簇的中心点cj(j=1,2,…,k)的更新如下所示:
(2)
(3)
(4)
在上文提到KHM具有易陷于局部最优的缺陷,因此融入群智能算法能够有效改善其性能,考虑到相关的改进算法较为相近,这里仅介绍最具有代表性的PSOKHM。由于PSO是一种被广泛研究的群智能优化算法,对于其具体原理本文不再详细介绍,可参考文献[2,8]了解。若k为聚类数,m为数据的维数,则一个粒子可表示为一个k×m列的一维实数向量,如图1所示。并且,PSOKHM的适应度函数即为KHM的目标函数。

X11X12…X1d…Xk1Xk2…Xkm
图1 PSOKHM中一个粒子的表达
PSOKHM的具体过程如下所示[2]:
1) 设置算法的基本参数,包括最大迭代次数IterCount,种群规模Psize,PSO的惯性权重因子w以及加速度因子c1和c2。
2) 初始化Psize个粒子的位置,并设置迭代次数Gen1=0。
3) 执行PSO算法进行搜索,迭代运行Gen2次后输出当前最优解,进入下一步操作。
4) 以当前最优粒子的位置作为聚类中心执行KHM算法,迭代运行Gen3次,获得新的聚类中心作为粒子的位置。
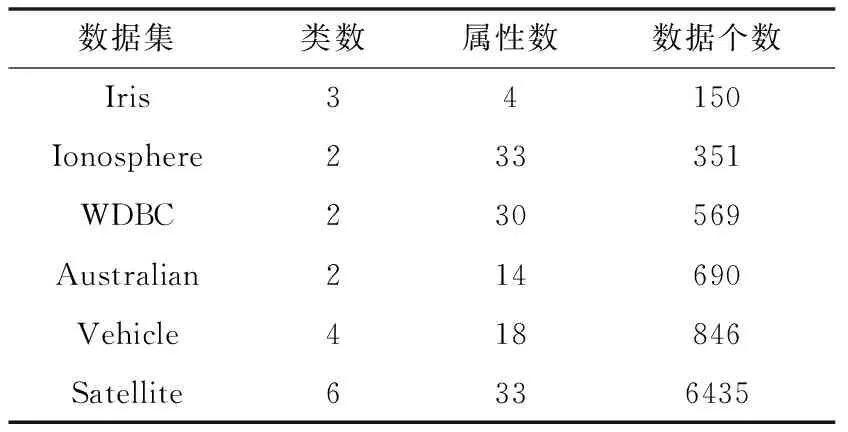
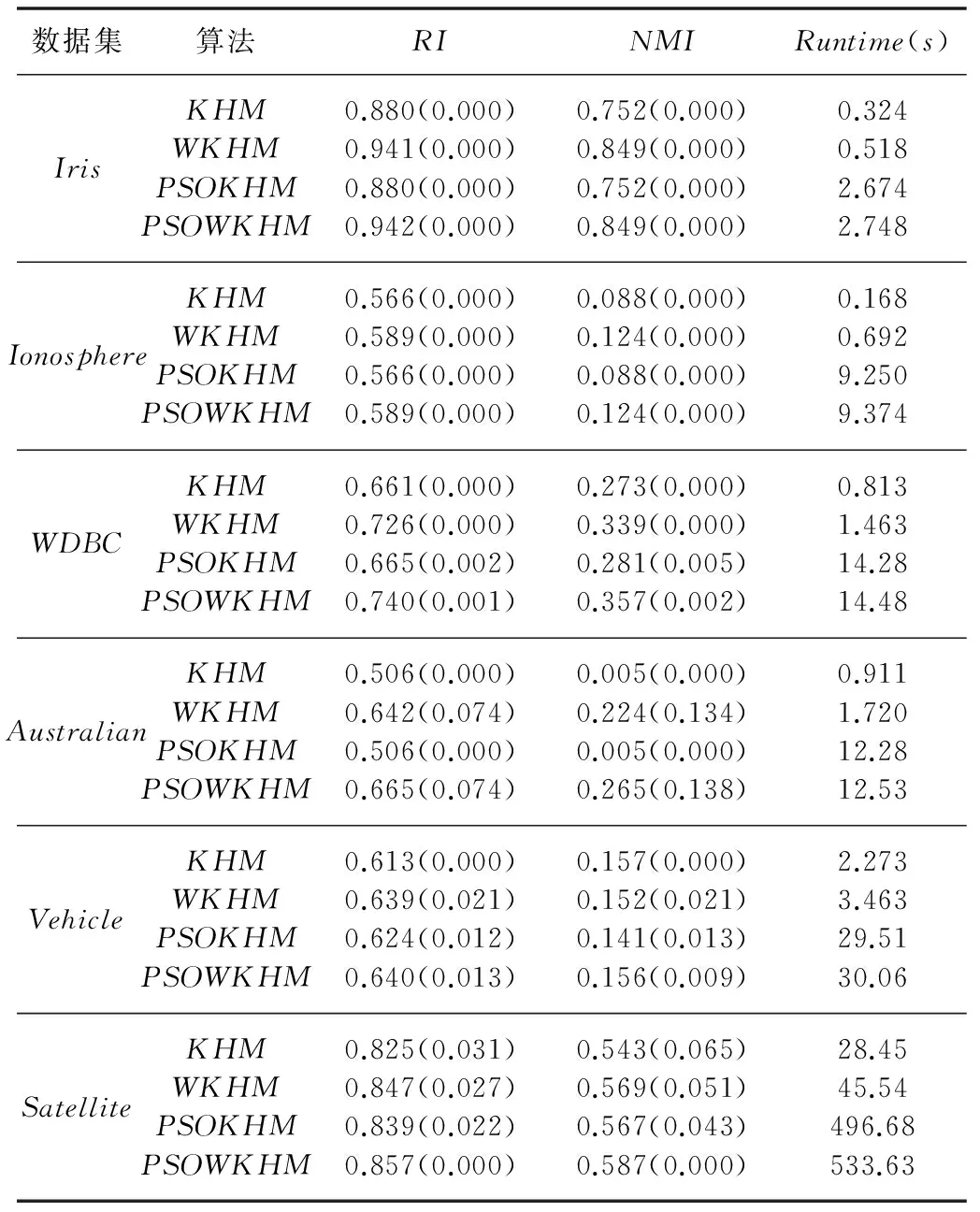
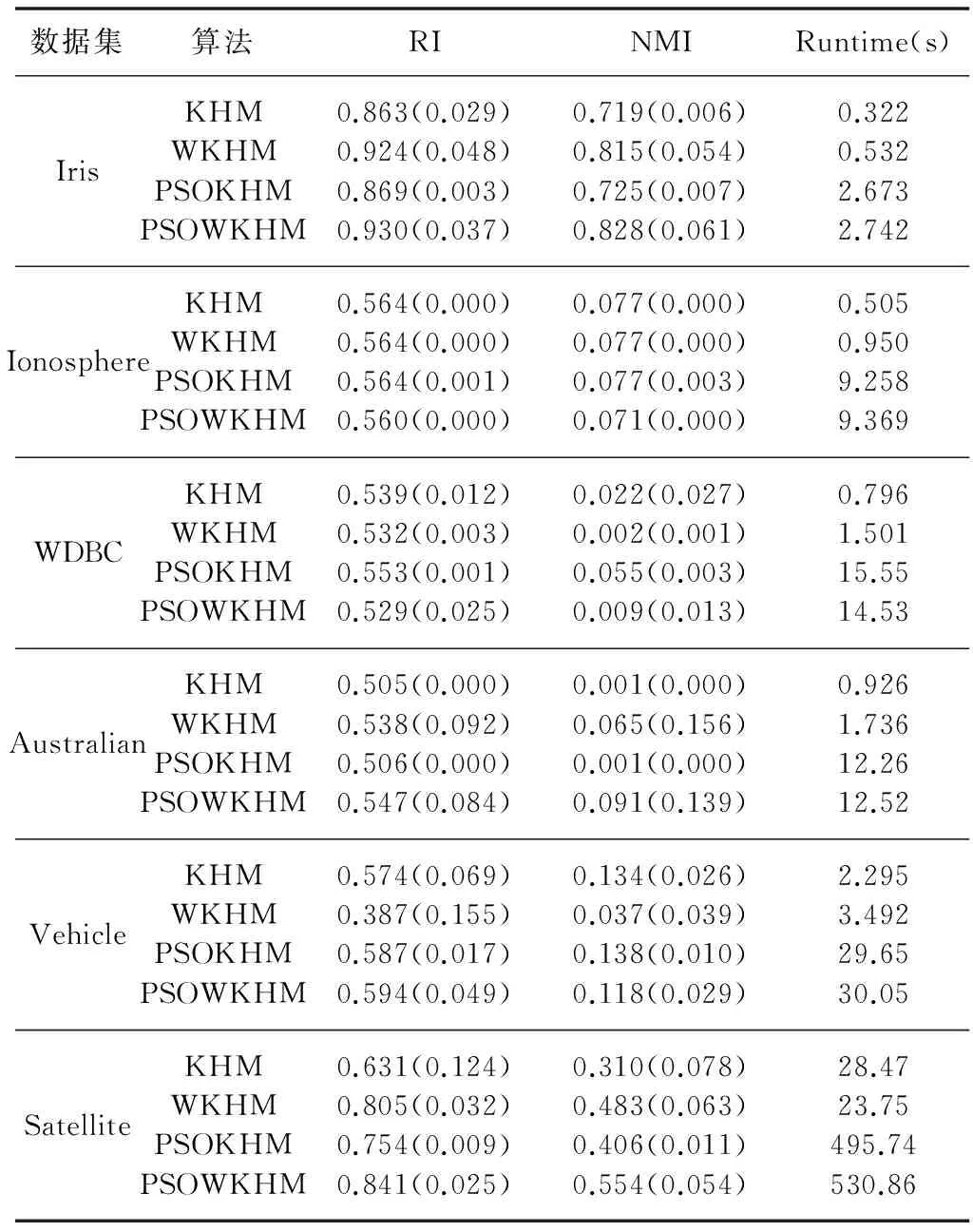
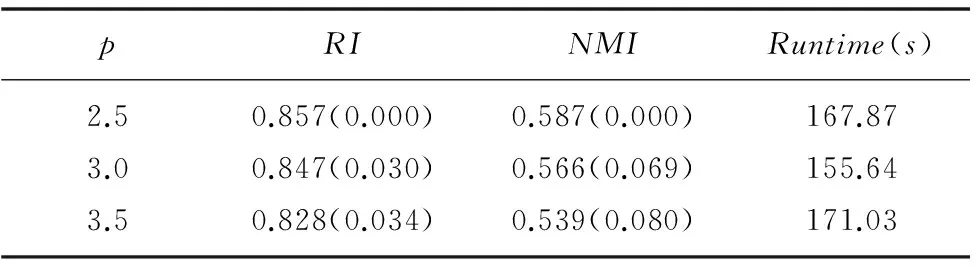
5) Gen1=Gen1+1,若Gen1 其中,文献[2]给出步骤2和步骤3中迭代次数Gen2和Gen3的取值分别分别为8和4,且文献[8]的KHM-MPSO中采用了同样的取值。然而,原文中均未给出确定这些迭代数的细节,可认为其为作者结合实验选用的值,能够满足绝大多数情况。 1.2 自动加权K均值 W-K-means算法是对K-means的拓展,将加权相异性度量引入到目标函数中,用wq(q=1,2,…,d)表示各维属性权重并通过指数参数β进一步控制其重要性,改进的目标函数为[12]: (5) 每次迭代过程中,属性权重的更新如下所示: (6) 2.1 属性加权K-调和均值算法 根据式(5)可见,属性权重引入了一个新的指数参数β,其对算法的性能具有比较重要的影响,对于不同数据集的最佳β值难以确定。考虑到KHM的距离度量已具有指数参数p,本文算法中未直接采用W-K-means的属性加权方式,而是采用加权欧氏距离dij(w)计算样本与类中心的距离。各属性权重同样用wq(q=1,2,…,m)表示,则WKHM算法的目标函数如下式所示: (7) 由于聚类过程是通过最小化目标函数进行,可将WKHM视为一种优化问题,即为: (8) 式(8)可通过格朗日乘法求解,函数表达式L可以表示为: (9) 其中λ为拉格朗日系数。 算法中包含聚类中心和属性权重这两个决策变量,需推导出它们的更新公式使得L始终能够收敛到一个局部最小值。首先求出L关于类中心cj(j=1,2,…,K)的偏导并使其为0: (10) 求出L关于wq(q=1,2,…,m)的偏导并使其为0,进而获得关于属性权重的计算式,如下所示: (11) (12) 结合式(12)以及式(8)中属性权重的约束条件即可求出λ的计算式,然后再代入到式(12)中即可获得属性权重最终的更新公式为: (13) 综上可得,WKHM聚类算法的具体流程为: Step1 初始化算法的基本参数,随机选取样本点并作较小的扰动作为初始的聚类中心。 Step2 根据式(8)计算目标函数的值。 Step4 根据式(2)计算新的聚类中心。 Step5 根据式(13)计算新的属性权重。 Step6 若达到最大迭代次数或者目标函数不发生明显变化则停止;否则,转Step2继续迭代运行。 2.2 融合粒子群算法的属性加权K-调和均值聚类 上述聚类算法在迭代过程中的时间复杂度主要依赖于距离的计算,且dij和dij(w)的计算复杂度均为O(knm),其中相应变量的含义均与上文相同。因此,KHM与WKHM的时间复杂度均为O(Gen3·knm),即混合聚类算法步骤4的时间复杂度,步骤3的时间复杂度为O(Gen2·Psize·knm),由于Gen3 3.1 实验数据以及评估标准 为了验证本文算法的有效性和可行性,选取了UCI数据库中比较常用的6个数据集对各算法的聚类性能进行测试,它们的具体特性如表1所示。 表1 实验数据集的特性 本文中通过两个常用的度量指标RI(rand index)和NMI(normalized mutual information)对聚类结果进行评估和比较分析。假定数据集真实的聚类为T,算法获得的聚类结果为C。令a、b、c、d分别表示同时属于T和C的相同类,属于T的相同类但是属于C的不同类,属于C的相同类但是属于T的不同类,以及同时属于T和C的不同类的数据的个数。则RI的计算公式如下所示: (14) NMI指标采用信息论中的熵计算每个真实的类与每个聚类结果的簇之间的平均互信息,若ni为类i中数据点的个数,nj为簇j中数据点的个数,nij为同时在类i和簇j中的数据点得个数,则NMI的计算公式为: (15) 它们的值均在0到1之间,且越大则表明聚类结果越好。此外,由于距离度量中属性加权的作用,WKHM目标函数的值相比KHM小很多,这里不对其进行比较。 3.2 实验结果与分析 为了分析算法的聚类性能,本文分别对KHM、WKHM、PSOKHM以及WPSOKHM进行对比分析。实验通过MATLAB2010b编程运行,计算机的硬件配置为:Intel Core P7450、CPU 2.13 GHz、2 GB RAM。各算法的参数设置为:KHM和WKHM的最大迭代次数Maxgen=100;PSOKHM的参数采用文献[3]中的Psize=18,w=0.7298,c1=c2=1.496,总迭代次数IterCount=5,且Gen1=8,需要注意文献[2]中数据集的复杂度相对较低,Gen2=4已无法满足求解要求,因此本文中为Gen2=10。分别取p=2.5、3、3.5时对聚类结果进行比较,每种算法独立运行20次,计算RI、NMI和运行时间的平均值,且为了进一步分析算法的稳定性,计算出RI和NMI的标准差记录至括号内,实验结果分别为表2至表4中所示。 表2 p=2.5时的实验结果对比 表3 p=3.0时的实验结果对比 续表3 表4 p=3.5时的实验结果对比 首先,根据表2至表4可以看出,在大多数情况下WKHM算法相对于KHM具有明显的提升,验证了采用加权欧氏距离对算法进行改进的可行性。尽管NMI指标的趋势与RI指标基本一致,但仍存在少数不一致的情况,比如在表3中PSOWKHM的RI值高于KHM,NMI值低于KHM,这表明采用多个指标进行对比分析的必要性。为进一步分析,以p=2.5时为例,根据表2中各算法的RI指标可见,WKHM算法对6种数据集分别提升了6.93%、4.06%、9.83%、26.88%、4.24%、2.67%。而PSOKHM算法对数据集Iris、Ionosphere、Australian的RI值均与KHM相同且标准差为0;对数据集WDBC的RI值取得了微弱的提升;仅对于数据集Vehicle和Satellite的RI值获得了相对较明显的提升,分别比KHM提高了1.79%、1.70%,但仍低于WKHM算法的改善效果。因此,可以看出现有的相关文献主要关注于将智能优化算法融入KHM中以克服局部最优的问题而忽略了对算法原理的进一步改进,具有一定的局限性,无法获得更好的聚类性能。并且,本文中同样将PSO融入WKHM算法中,以同时利用了属性权重的改进和智能算法全局搜索的优势。其中,对于数据集Iris、Ionosphere和Vehicle,PSOWKHM的RI值相对于WKHM没有明显变化,而对于数据集WDBC、Australian和Satellite提高了1.93%、3.58%、1.18%,可见算法性能得到了进一步的提高。此外,值得注意的是表2中除数据集Satellite,KHM算法对其他数据的聚类指标值的标准差均为0,有效验证了其对初始聚类中心不敏感。由于KHM算法中p(通常p≥2)的选取对其性能具有一定的影响,本文中分别选取大多数文献中采用的2.5、3.0和3.5进行分析。可见,KHM对于数据集Iris、Ionosphere和Australian而言,p的选取对算法的性能的影响不是很明显,而对于数据集WDBC、Vehicle和Satellite则相对较为明显。WKHM同样存在对参数p敏感的问题,在某种程度上可能更明显,比如WKHM对于WDBC和Vehicle在2.5和p=3.0时的性能均优于KHM,而在3.5时比后者更差。为了更直观分析,图2给出WKHM以及PSOWKHM取不同p值时对各数据集的RI指标值,其中横坐标的1~6分别表示数据集Iris、Ionosphere、WDBC、Australian、Vehicle、Satallite。由图中可见,WKHM和PSOWKHM在p=2.5和p=3.0时对各数据集的性能均较为接近,而在p=3.5时对一些数据集出现了明显的下降。此外,图2中(a)显示WKHM对于Vehicle在p=3.5出现骤降,而(b)显示PSOWKHM对于Vehicle在p=3.5并没有明显下降,表明融入PSO后有效抑制了陷入局部最优的问题。综合分析,本文取p值在[2,3]内可使得改进算法对各数据集能获得比较满意的结果,并且由(b)中可见PSOWKHM在p=2.5时相对于p=3.0时具有较小程度的优势。 由表2-表4中各算法的平均运行时间可见,WKHM较KHM的时间有较小的增加,这是由于增加了属性权重的计算过程,其中WKHM对Satellite的运行时间更短是由于其提前终止使总迭代次数更小。两种混合聚类算法较原算法的平均运行时间均具有较大的增加,特别是对样本数较大的Satellite数据集的运行时间比较长,这是由于PSO执行全局搜索需要较大的时间开销。然而,在步骤2中若PSO始终执行Gen2次迭代可能会增加不必要的计算开销,因此这里采用一个较小的阈值ε=10^(-4)判断是否终止。在PSO优化过程中,计算第t次迭代最优解的适应度值fbest(t)与前一次迭代最优解的适应度值fbest(t-1)的差值,当满足fbest(t)-fbest(t-1)<ε时停止PSO迭代,输出当前最优解并继续执行步骤3。这里以较大的数据集Satellite进行分析,采用阈值ε判断终止的实验结果如表5所示。可见,设定阈值后PSOWKHM对Satellite的性能并没有下降,而运行时间减少了很多,从而有效提高了算法的运行效率。 图2 本文两种算法对各数据集的RI值 表5 PSOWKHM中设定阈值后对Satellite的实验结果 尽管如此,融入PSO的混合聚类算法在时间性能方面仍处于劣势,因此对于WKHM和PSOWKHM可根据具体问题进行选取。考虑到WKHM较后者的聚类性能并没有较明显的降低而在时间效率方面具有明显的优势,一般情况下可优先采用,若对于聚类准确度要求较高时则可选用PSOWKHM,以降低算法陷入局部最优的可能性。 由于KHM算法在聚类过程中将所有权重的作用视为相等而具有一定的局限性,本文利用属性加权欧氏距离提出一种改进的WKHM算法,且在聚类过程中自动更新属性权重。并且,为了进一步提高算法的聚类性能,将其与PSO相结合获得新的混合聚类算法。实验结果有效验证了改进算法的可行性,对各数据集的性能均具有较为明显的改善。考虑到不同属性对不同类的聚类作用也存在差异,而若将向量加权欧氏距离改为矩阵加权欧氏距离则会增加算法推导的复杂性,后续将继续研究将软子空间的原理引入到KHM中,以期进一步提升算法的性能。 [1] Zhang B.Generalized k-harmonic means[J].Hewlett-Packard Laboratoris Technical Report,2000. [2] Yang F Q,Sun T E L,Zhang C H.An efficient hybrid data clustering method based on K-harmonic means and Particle Swarm Optimization [J].Expert Systems with Applications,2009,36(6):9847-9852. [3] Jiang H,Yi S,Li J,et al.Ant clustering algorithm with K-harmonic means clustering [J].Expert Systems with Applications,2010,37(12):8679-8684. [5] Carrizosa E,Alguwaizani A,Hansen P,et al.New heuristic for harmonic means clustering [J].Journal of Global Optimization,2014,1-17. [6] Hung C H,Chiou H M,Yang W N.Candidate groups search for K-harmonic means data clustering [J].Applied Mathematical Modelling,2013,37(24):10123-10128. [7] Abdeyazdan M.Data clustering based on hybrid K-harmonic means and modifier imperialist competitive algorithm [J].The Journal of Supercomputing,2014,68(2):574-598. [8] Bouyer A,Farajzadeh N.An Optimized K-Harmonic Means Algorithm Combined with Modified Particle Swarm Optimization and Cuckoo Search Algorithm [J].Journal of Intelligent Systems,2015. [9] 汪中,刘贵全,陈恩红.基于模糊 K-harmonic means 的谱聚类算法 [J].智能系统学报,2009,4(2):95-99. [10] 刘娜,肖智博,鲁明羽.基于模糊 K-调和均值的单词-文档谱聚类方法 [J].控制与决策,2012,27(4):501-506. [11] Wu X,Wu B,Sun J,et al.A hybrid fuzzy K-harmonic means clustering algorithm [J].Applied Mathematical Modelling,2015,39(12):3398-3409. [12] Huang J Z,Ng M K,Rong H,et al.Automated variable weighting in k-means type clustering [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(5):657-668. [13] Jing L,Ng M K,Huang J Z.An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data [J].IEEE Transactions on Knowledge and Data Engineering,2007,19(8):1026-1041. [14] 李仁侃,叶东毅.属性赋权的 K-Modes 算法优化 [J].计算机科学与探索,2012,6(1):90-96. [15] Ji J,Bai T,Zhou C,et al.An improved k-prototypes clustering algorithm for mixed numeric and categorical data [J].Neurocomputing,2013,120:590-596. [16] Ferreira M R,de Carvalho F d A.Kernel-based hard clustering methods in the feature space with automatic variable weighting [J].Pattern Recognit,2014,47(9):3082-3095. [17] Zhang L,Pedrycz W,Lu W,et al.An interval weighed fuzzy c-means clustering by genetically guided alternating optimization [J].Expert Systems with Applications,2014,41(13):5960-5971. K-HARMONIC MEANS CLUSTERING BASED ON AUTOMATED FEATURE WEIGHTING Fan Guiming Zhang Guizhu (School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,Jiangsu,China) K-harmonic means algorithm has the disadvantage of viewing all features as the same importance in its distance metric.In light of this,we proposed an improved clustering algorithm which takes the advantage of automated feature weighting.In objective function of the algorithm,we replaced the conventional Euclidian distance with the weighted Euclidian distance,and proved the feature weight update mechanism which enables the algorithm to be converged.In order to further improve the clustering performance,we integrated the particle swarm optimisation into the feature weighting clustering algorithm so as to suppress its problem of being trapped into local optimum,in which we used both the centres of clusters and the value of feature weight to represent the position of each particle for optimisation.Tests result on UCI datasets showed that the clustering index of the proposed algorithm has raised about 9 percents,so our method is more accurate and stable. K-harmonic means Clustering Feature weighting Particle swarm optimisation 2015-10-09。江苏省自然科学基金项目(BK20140165)。范桂明,硕士生,主研领域:数据挖掘。张桂珠,副教授。 TP301.6 A 10.3969/j.issn.1000-386x.2016.11.055

2 自动属性加权的K-调和均值聚类
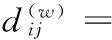
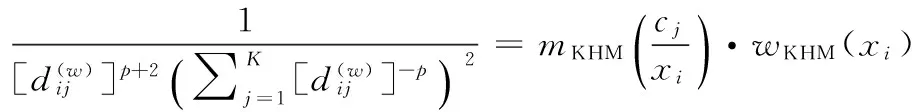
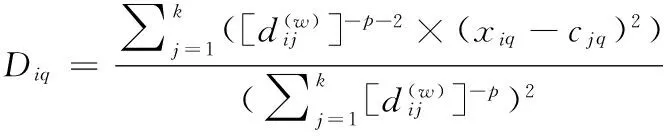

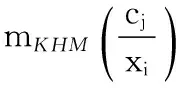
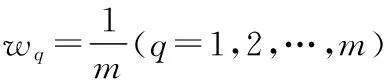
3 实验与分析



4 结 语
