动态搜索半径的果蝇优化算法

高雷阜 赵世杰 徒 君 于冬梅

(辽宁工程技术大学优化与决策研究所 辽宁 阜新 123000)



动态搜索半径的果蝇优化算法

高雷阜 赵世杰*徒 君 于冬梅

(辽宁工程技术大学优化与决策研究所 辽宁 阜新 123000)

针对传统果蝇优化算法FOA(Fruit Fly Optimization Algorithm)固定搜索半径导致后期局部寻优性能弱、收敛缓慢的问题，提出一种动态搜索半径的果蝇优化算法DSR-FOA(Fruit Fly Optimization Algorithm With Dynamic Search Radius)。该算法前期以较大搜索半径保证全局寻优性能，而后期搜索半径随迭代次数动态递减以保证局部寻优性能，有效地实现算法全局与局部寻优性能的均衡。其次，针对传统果蝇优化算法不适于优化变量的区间设定问题，通过初始搜索半径设定和平移变换等技术提出一种有效的区间限定方法。数值实验结果表明：改进算法具有较好的寻优精度和预测标准差等指标，验证了算法的有效性和可行性。

果蝇优化算法 搜索半径 平移变换 基准测试函数

0 引 言

果蝇优化算法[1，2]FOA是学者潘文超受果蝇觅食行为启发，于 2011 年提出的一种新的仿生智能优化算法。其模仿果蝇通过优越的嗅觉和视觉来找寻、发现食物，主要利用嗅觉搜索实现果蝇个体多样性的提高和较大的搜索范围，利用视觉搜索实现果蝇个体的快速收敛。该算法具有调节参数少、寻优速度快和易于实现等优点而在一些科学和工程领域[3-5]得到有效应用。目前FOA算法的研究方向主要有搜索半径的改进[6，7]、味道判定函数的改进[8，9]和种群多样性的设置[10，11]等方面。

传统FOA算法中搜索半径是保持固定不变的，虽能保证算法前期较大的搜索空间以实现较好的全局搜索性能，但却严重影响了算法后期的局部搜索性能，而造成后期寻优性能弱、收敛缓慢的不足。对此本文改进了传统FOA算法的迭代搜索半径，提出了一种动态搜索半径的果蝇优化算法，以实现果蝇群体在全局与局部均能保持较好的搜索性能。同时由于果蝇代表的解只能为正值与优化问题可能存在负值区间的矛盾性，基于初始搜索半径的设定和平移变换等技术提出了一种区间限定方法，最后，将改进算法用于基准测试函数的优化求解。

1 果蝇优化算法

果蝇优化算法是受果蝇觅食行为启发而提出的一种仿生智能优化算法，是一种全局优化方法。果蝇是飞行昆虫，通过自身嗅觉和视觉对外部环境极为敏感的特性，先利用嗅觉器官很好地获取漂浮在空气中的各种气味，确定出食物源的大体位置；在飞近食物后再利用视觉发现食物与同伴聚集的位置，同时往该方向飞去。在嗅觉记忆与视觉记忆的协同作用下，模拟果蝇群体搜寻食物的过程。FOA算法迭代寻优过程可归纳为以下几步：

Step1 果蝇种群规模Sizepop和最大迭代次数Genmax的设置；果蝇群体位置的随机初始化axisX和axisY：

(1)

其中，x0和y0为常数。

Step2 赋予果蝇飞行的搜索半径R与随机方向D，确定出第k代果蝇群体第i个个体利用嗅觉搜寻食物所得的新位置坐标：

(2)

其中，R(·)为果蝇个体利用嗅觉觅食的固定搜索半径；D(·)=2rand()-1为[-1,1]间的一个随机数，表示果蝇个体的随机觅食方向(正值表示正方向；负值表示负方向)。

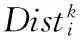
(3)

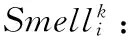
(4)

(5)

Step6 果蝇群体通过视觉飞到式(5)所保存的位置，生成新的果蝇群聚位置：

(6)

Step7 判断是否满足终止条件，即判断迭代次数k是否达到最大迭代次数Genmax。若是则输出最优味道浓度和判定值，反之k加1，并跳转执行Step2。

2 动态搜索半径的果蝇优化算法

2.1 改进思想

传统FOA算法在Step2中，搜索半径R是保持固定不变的，即每代果蝇群体的果蝇个体在利用嗅觉觅寻食物时都是以固定半径R向周围随机搜索的。为保证FOA算法具有较好的全局寻优性能，同时避免陷入局部极值等问题，一般搜索半径R设置为一个相对较大的值。这样做，虽然保证了FOA算法前期的较好全局寻优性能，但同时导致了另外一个问题：在算法迭代寻优后期，由于果蝇群体仍在较大的搜索空间中继续寻优，从而导致局部寻优性能较弱、寻优效率相对较低和收敛缓慢等问题。

由传统FOA中搜索半径R存在的问题分析可以发现：搜索半径R的设置直接影响着FOA算法的优化性能。为保证算法既具有较好的全局寻优性能，又具有较强的局部寻优性能，搜索半径R的设定应遵循如下原则：前期搜索半径R为一个相对较大的值以保证全局寻优性能，后期搜索半径R则应为相对较小的值以保证局部搜索性能。

文献[6]改进提出的DS-FOA算法中，搜索半径R满足的函数关系式为：

(7)

其中，变量Iter为果蝇群体的当前迭代次数，常量Itermax为最大迭代次数，常量Rmax为搜索半径的初始最大值。

文献[7]改进提出的IFFO算法中搜索半径R满足的函数关系式为：

(8)

其中，常量Rmin为搜索半径的最小值。

在DS-FOA算法和IFFO算法中，搜索半径R前期下降较为迅速(如图1所示)，并不能较好地保证算法的全局优化性能，在一定程度上降低了FOA算法的全局优化性能。综合考虑传统FOA算法、DS-FOA算法和IFFO算法中存在的问题，本文对果蝇群体搜索半径R进行改进，提出了动态搜索半径的果蝇优化算法DSR-FOA。搜索半径定义式为：

(9)

其中，跳转因子μ和指数因子α均为(0,1)间的一个常量。

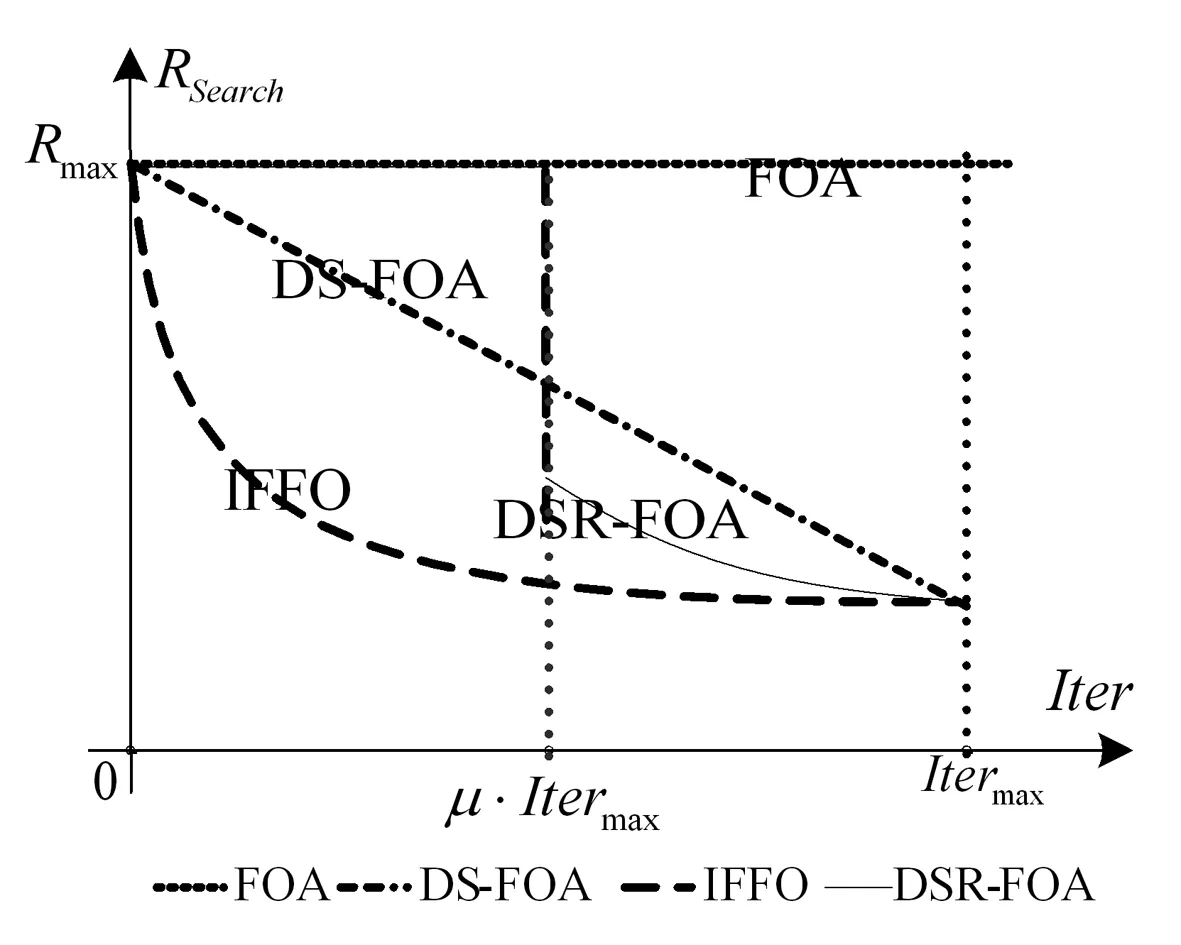
图1 FOA算法的搜索半径对比图

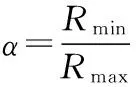
2.2 DSR-FOA算法优化连续函数

由图1可知：DSR-FOA算法在迭代前期具有较大的搜索半径，保证了较好的全局寻优性能；后期搜索半径相对减小有利于保证算法的局部寻优性能，从而使算法实现全局与局部寻优性能的较好均衡。

DSR-FOA算法可用于连续函数的优化求解。设连续函数的定义式为：

(minf(x)

s.t. xi∈[m,n] i=1,2,…,N)

(10)

其中，N表示函数f(·)中的变量数目。

传统FOA算法的味道浓度判定值(即问题的解)是通过搜索半径R所定位置以距离的形式来表示的，且只能取正值，这与测试函数中变量取值区间可能存在负区间是相矛盾的。为解决这种矛盾，利用搜索半径的初始设定和平移变换等技术提出了一种适应于FOA算法的变量区间设定方法。该方法首先对初始搜索半径Rmax根据变量取值区间进行设定，再利用区间平移变换实现味道浓度判定值落入变量取值区间内。具体操作方法为：当优化函数变量取值区间[m,n](默认测试函数中|m|和|n|均大于1)的界值m和n同号时，Rmax=1/max{|m|,|n|}，同时利用循环保证生成Sizepop个Si介于[m,n](m和n均正时)，则Si即表示函数变量(若m和n均负时，需保证(-Si)介于[m,n]，此时(-Si)表示函数变量)；当变量取值区间界值m和n异号时，Rmax=1/|n-m|，同时保证生成Sizepop个Si小于等于|n-m|，则(Si-|m|)表示函数变量。利用DSR-FOA算法对优化函数的执行伪码(变量取值区间为[-m,m],m>1)为：

Algorithm:DSR-FOA AlgorithmParameters:Population size(sizepop),Maximum,iterations(Itermax),Search Radius(Rmax),Variable numbers(n),Constant μ and α

Output:Best Solution S*

Set sizepop,Itermax,Rmax,n,μ,α

While 1

∥根据式(1)和式(2)初始化种群位置(Xaxis,Yaxis)

∥计算S0并判定其中有效变量的数目

IF sum(S0<=2m)==n

break;

END

END

Iter=1

Repeat

∥根据式(9)更新搜索半径RIter

∥嗅觉觅食阶段

While 1

∥根据RIter利用式(2)更新种群位置(Xaxis,Yaxis)

∥计算SIter并判定其中有效变量的数目

IF sum(SIter<=2m)==n

break；

END

END

∥视觉觅食阶段

END

Iter=Iter+1

Until Iter==Itermax

3 实验仿真

3.1 实验设计

为验证DSR-FOA算法的优越性，以FOA算法、DS-FOA算法和IFFO算法作为对比算法，通过6个基准测试函数的仿真实验结果来说明DSR-FOA算法的有效性和可行性。6个基准测试函数的函数名称、函数形式和变量区间等信息如表1所示(其中Schaffer函数为2维，其余为30维)。

表1 基准测试函数信息

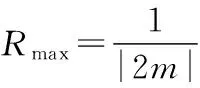
3.2 实验结果与分析

根据3.1节中6个测试函数的变量取值区间和参数设置情况，利用4种算法对6个测试函数进行数值实验，各算法性能的评价指标选用最优值(best)、最差值(worst)、平均值(mean)和标准差(std)共4个统计指标。各测试函数的30次实验的统计平均结果如表2所示。

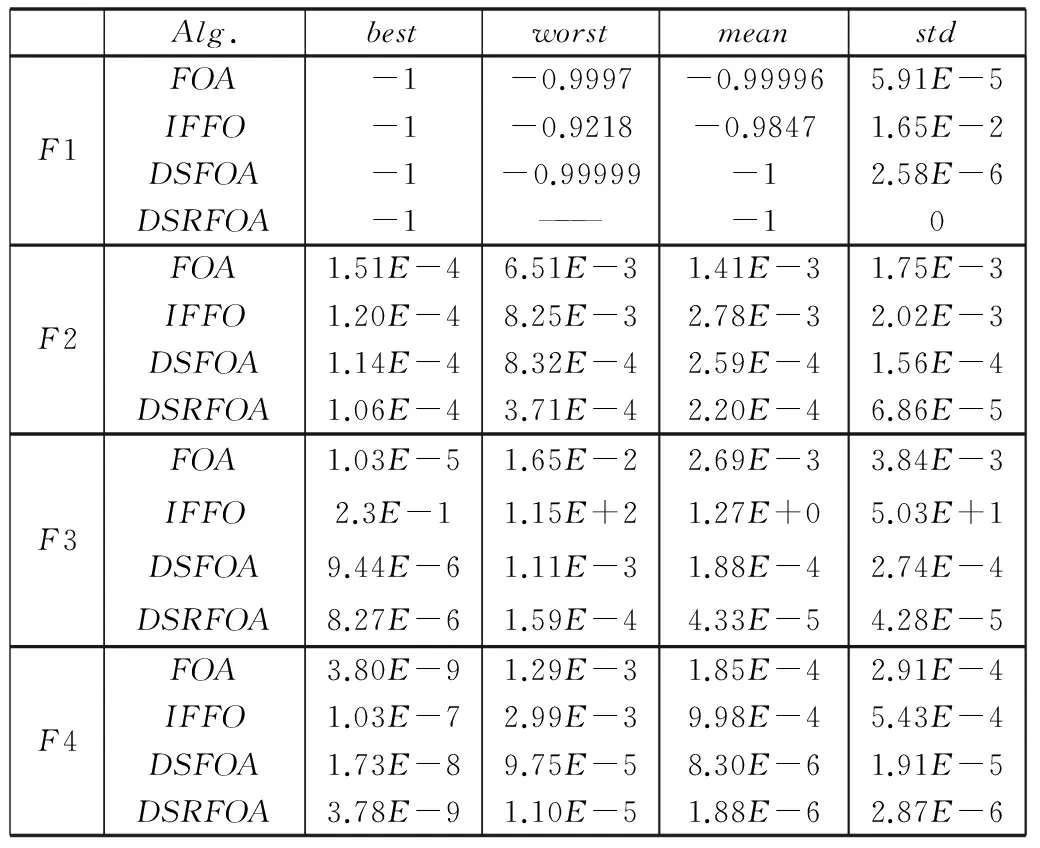
表2 四种算法对测试函数的结果

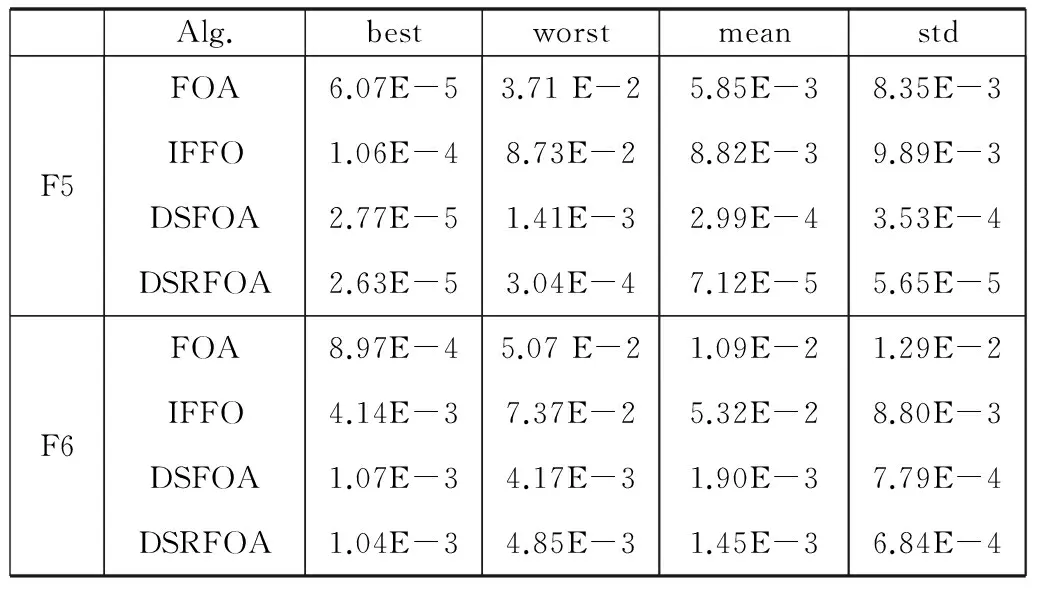
续表2

由表2可知：对6个基准测试函数的实验结果中，DSR-FOA算法的4项评价指标均优于FOA算法、IFFO算法和DS-FOA算法，具有较好的平均函数值和较小的测试标准差，说明了DSR-FOA算法具有较好的优化精度和较强的鲁棒性；并具有最优的best指标(除F6)，表明改进算法保证了较好的最优预测性能；同时有最小的worst指标(除F6)，说明改进算法即使在最坏极端情况下也能保持较好的预测性能，在实际应用中有利于降低未知情形下的可能损失和资源浪费，从而在一定程度上验证了改进算法的较好优越性能。

为更直观形象地展示4种算法对各测试函数的迭代寻优性能，绘制了算法的迭代寻优对比曲线，如图2-图7所示。

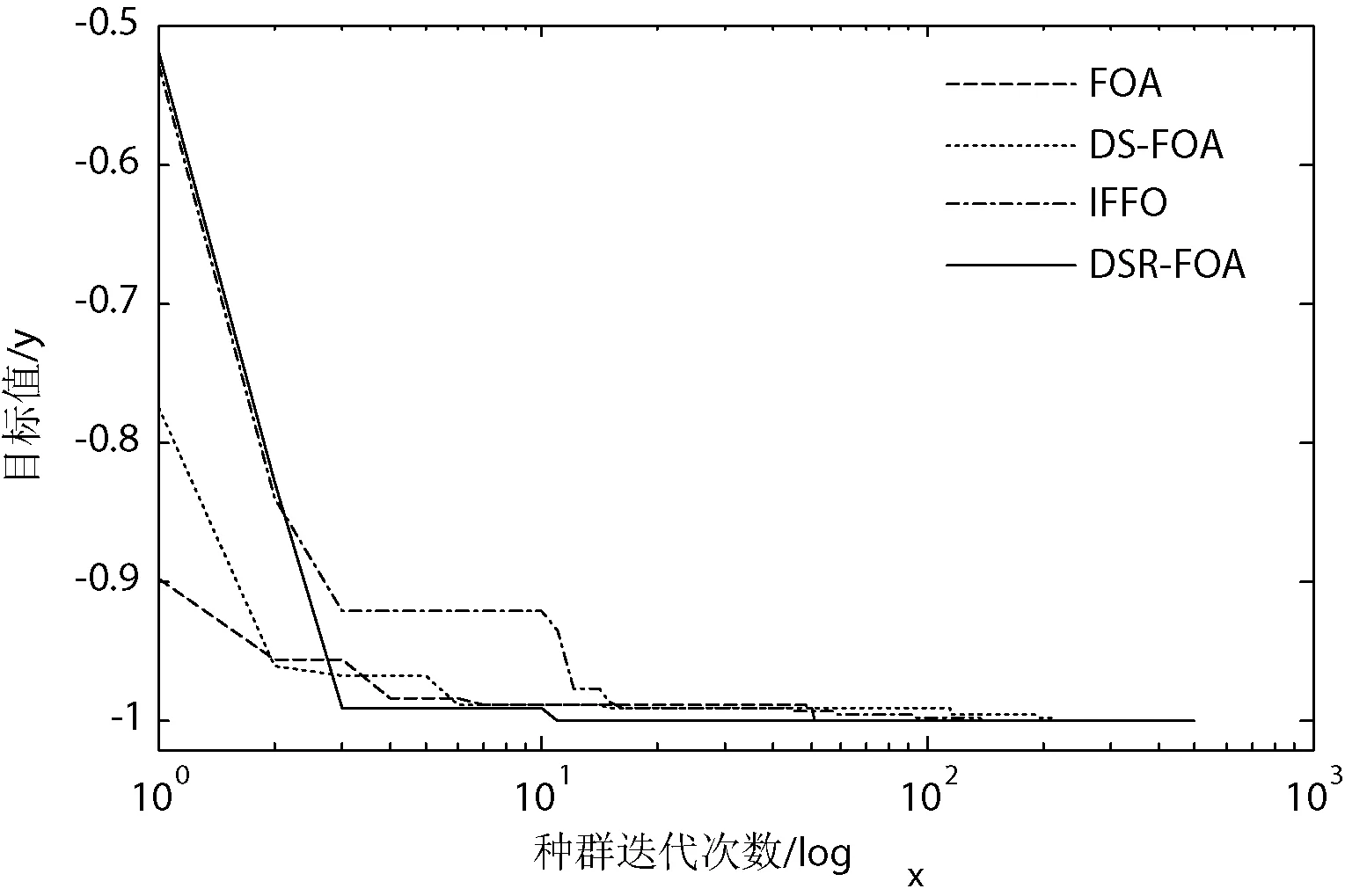
图2 测试函数Schaffer的对比曲线

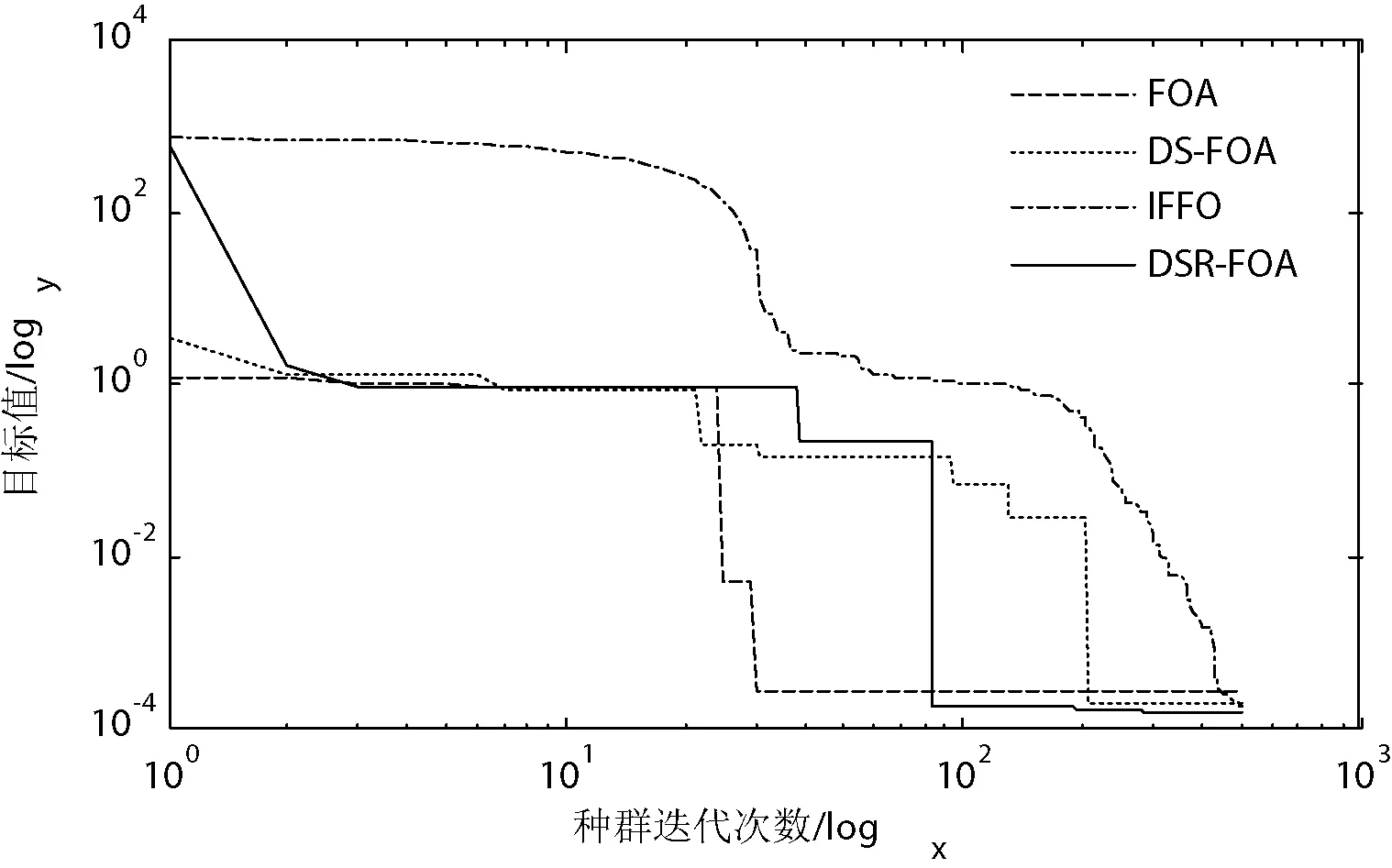
图3 测试函数Griewank的对比曲线

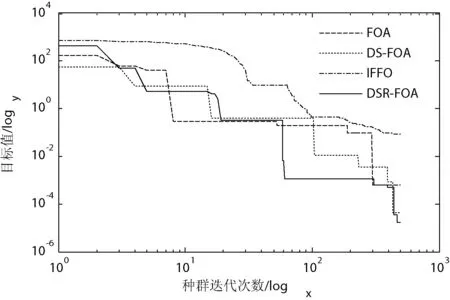
图4 测试函数Rosenbrock的对比曲线

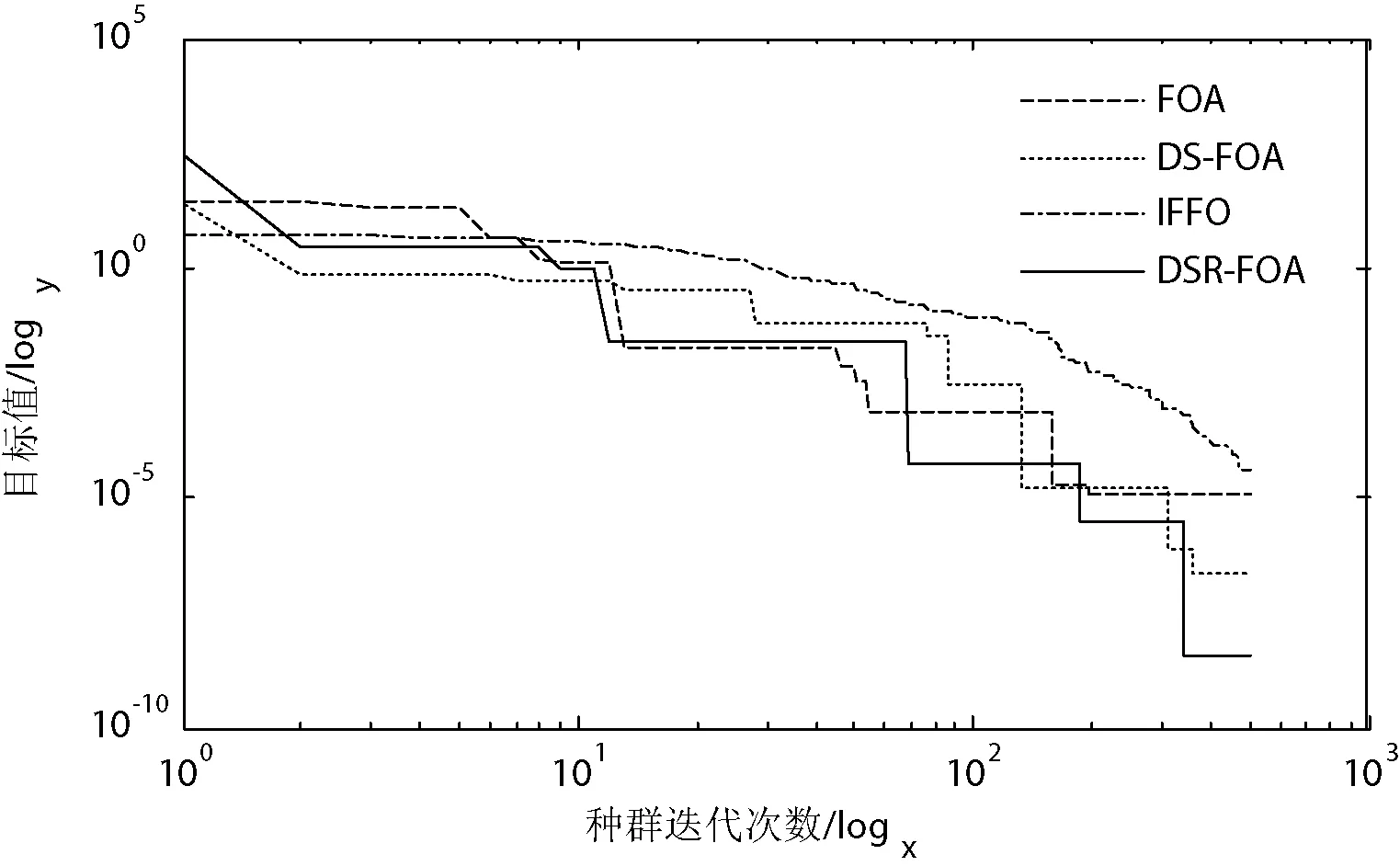
图5 测试函数Rastrigin的对比曲线

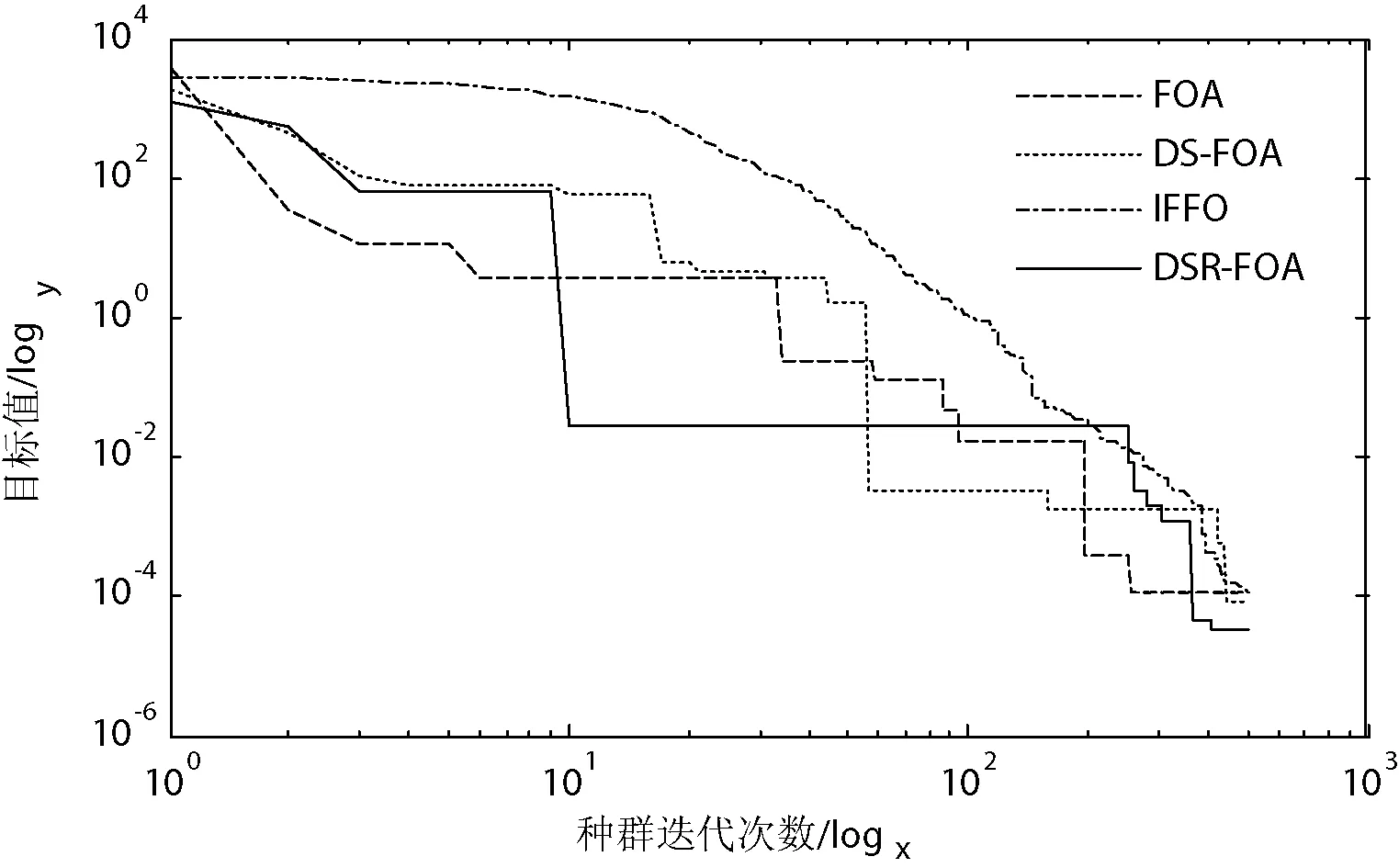
图6 测试函数Quadric的对比曲线

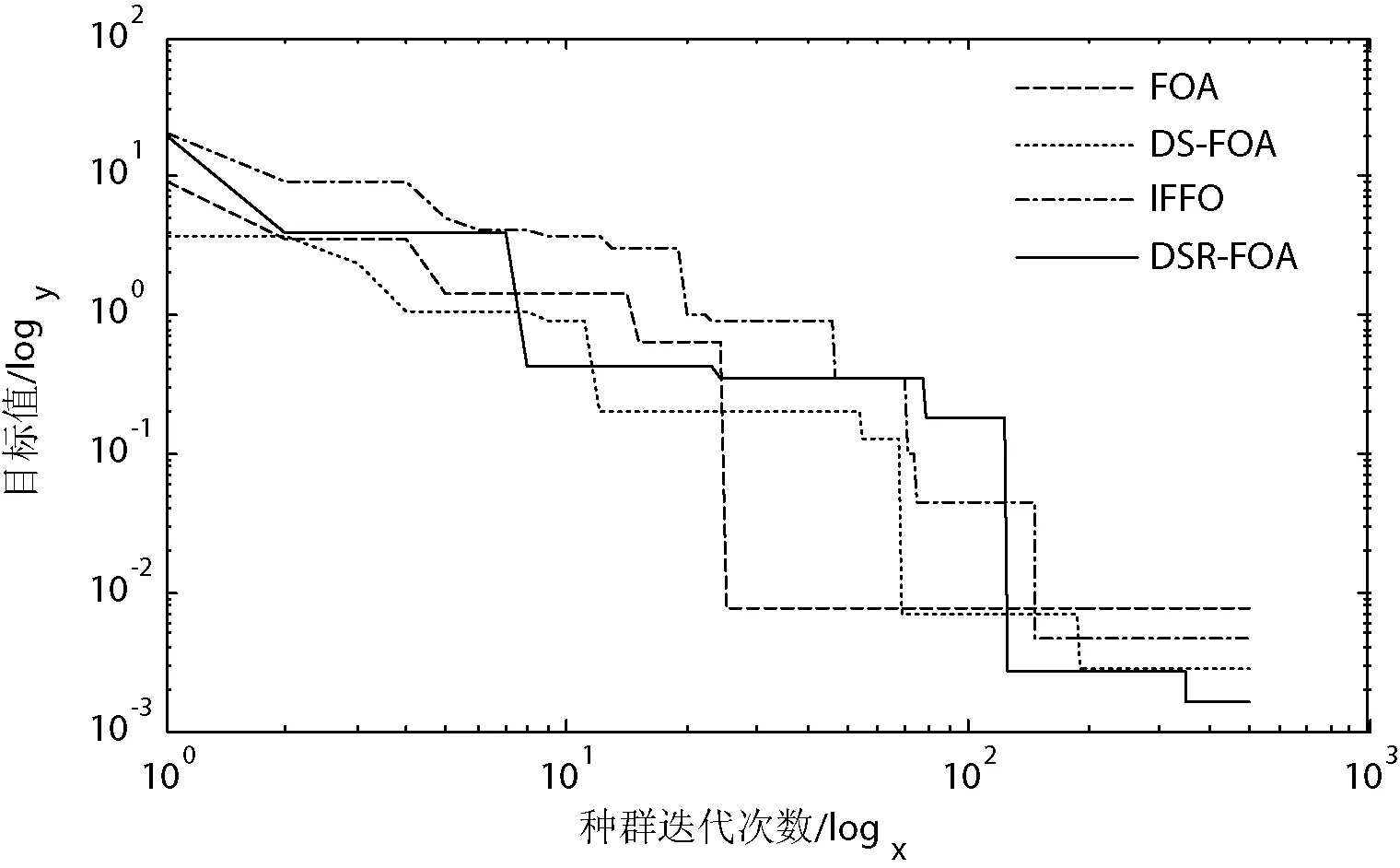
图7 测试函数Ackley的对比曲线

由图2-图7可以看出：在对各测试函数的迭代寻优过程中，DSR-FOA算法与其他算法相比不仅保证了算法前期较好的全局寻优性能，即使在初始解离最优解相对较远的情形下也能迅速地趋近于函数的近似最优解(近优解)；而且在算法后期有效地实现了对该近优解的进一步局部搜索，以较好的局部寻优性能来获得一个更好的近优解。因此，在一定程度上说明了改进算法有效地均衡全局寻优性能和局部寻优性能，具有较强的迭代寻优性能。同时，改进算法不仅对单峰测试函数具有较好的寻优性能，而且对Schaffer和Ackley等多峰函数也表现出较好的寻优性能和收敛精度，进一步验证了DSR-FOA算法的优良寻优性能。

3.3 2个因子对DSR-FOA算法的性能影响

DSR-FOA算法的优化性能受跳转因子μ和指数因子α的共同影响，因此需要研究2个因子对算法的性能影响。

本节以Quadric函数为测试函数，参数设置情况同3.2节，跳转因子μ和指数因子α分别属于[0，1]和(0，1]，且自增步长为0.02，共得到51×50组(μ,α)的参数组合。对各参数组合(μ,α)均进行30次实验，以30次实验平均值为最终实验结果，并绘制2个因子对DSR-FOA算法性能影响，如图8所示。

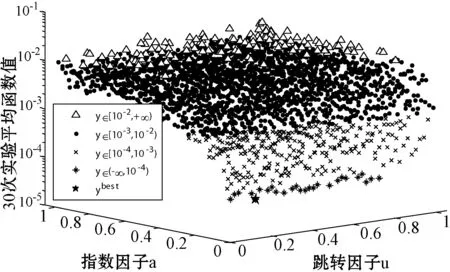
图8 2个因子对DSR-FOA算法性能的影响

由图8可知，不同因子组合(μ,α)对DSR-FOA算法性能的影响是不同的：越趋近于(1,1)组合，改进算法的预测精度越弱，原因是改进算法越趋退化为传统FOA算法而导致后期局部寻优性能减弱；指数因子α越趋近于0，改进算法的预测精度越高，表明算法后期对近优解的局部寻优性能越强；跳转因子μ在一定区间内对改进算法性能的影响差异是不明显的，即表明跳转因子μ在一定区间内对改进算法而言均具有较好的全局寻优性能，在算法前期都可迅速获得所研究问题的一个近优解。因此，在实际应用中可通过跳转因子μ和指数因子α的合理设置有效地实现算法全局寻优性能和局部寻优性能的良好均衡，以提高算法的寻优效率和优化精度。图8中星形表示最优解，其坐标为(0.12,0.02)。

为更直观地分析因子μ和α对改进算法性能的影响，绘制图9以研究在固定某一因子条件下分析另一个因子对改进算法的独立影响。其中(a)是固定指数因子α，研究跳转因子μ对DSR-FOA算法性能的影响；(b)是固定跳转因子μ，研究指数因子α对DSR-FOA算法性能的影响。

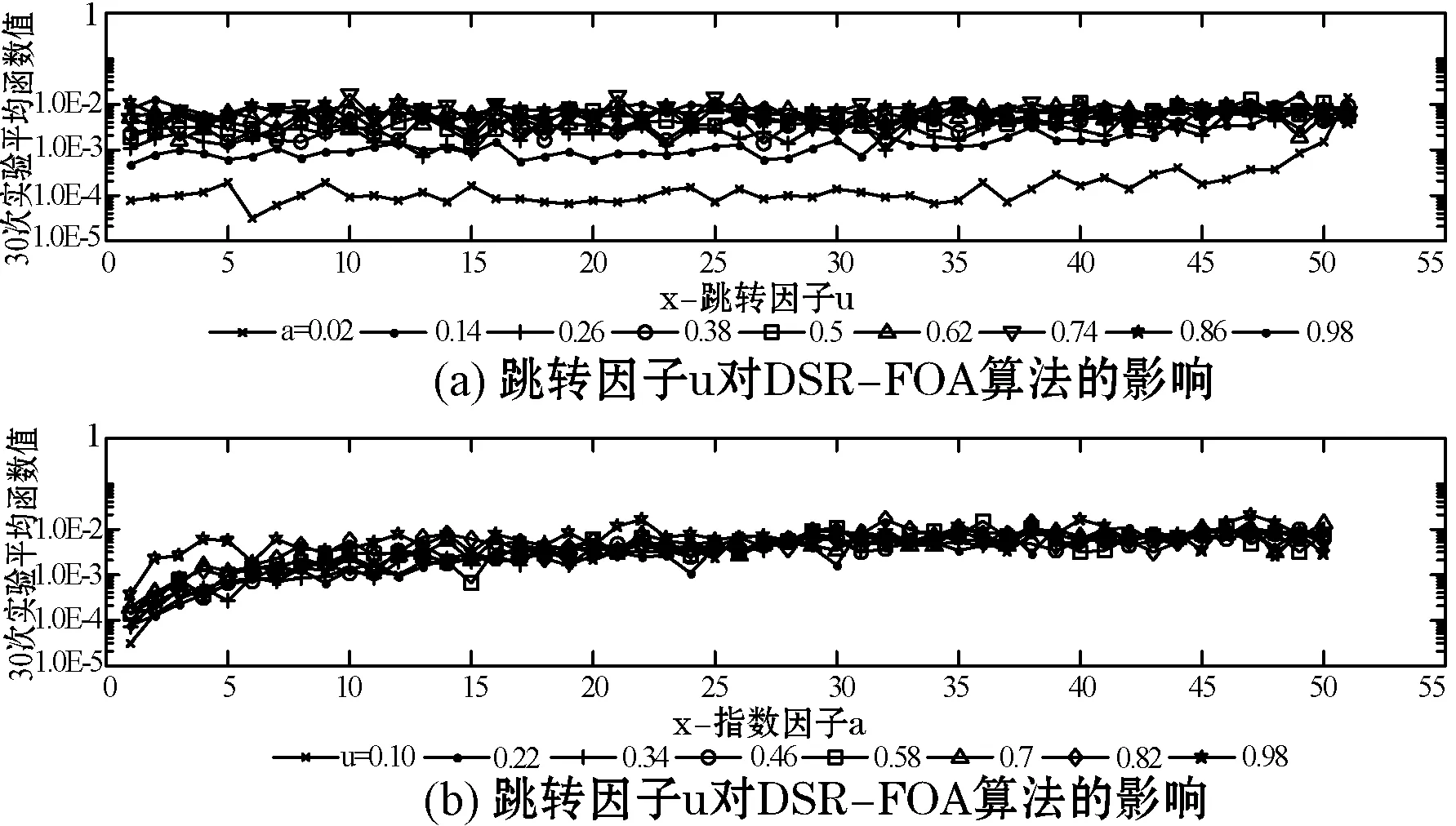
图9 不同影响因子值对DSR-FOA算法的性能影响分析图

在固定指数因子α的前提下，由图9(a)的分析可知：在固定α值较小时，跳转因子μ递增变化的前半段对改进算法预测性能的影响是不明显的，但在后半段(即μ→1时)，算法的预测性能越趋减弱(即min问题的预测值越趋增大)。在固定α值超过一定范围越趋近于1时，跳转因子μ的递增变化对改进算法预测性能的影响差异是越趋不显著的，原因正是由于改进算法越趋退化为传统FOA算法。在固定跳转因子μ的前提下，由图9(b)的分析可知：针对不同跳转因子μ的固定值，DSR-FOA算法的预测性能均随着指数因子α的增大而越趋减弱，甚至在预测曲线后半段出现预测性能“差异性不显著”的现象。鉴于上述分析，在实际应用中一般建议DSR-FOA算法中因子的设置情况为：跳转因子μ∈[0.1,0.35]、指数因子α∈(0,0.15]。

4 结 语

鉴于传统果蝇优化算法中搜索半径固定不变而导致后期局部搜索性能较弱和收敛缓慢的问题，本文提出了一种动态搜索半径的果蝇优化算法——DSR-FOA算法。该算法前期具有较大的搜索半径，保证了较好的全局搜索性能；同时后期搜索半径随迭代次数动态减小，有利于强化算法的局部搜索性能。该算法有效地实现了全局搜索性能和局部搜索性能的均衡，有利于迅速有效地获得较为优异的问题解。

由于果蝇优化算法所代表的解(浓度判定值)只能取正值，与所研究问题的解可能存在负取值区间是相矛盾的。因此，本文通过搜索半径的初始设定和平移变换等技术提出了一种有效的优化变量取值区间的限定方法，以实现果蝇优化算法对变量取值区间的较好适用性。同时将DSR-FOA算法用于基准测试函数的寻优中，数值实验结果验证了改进算法的有效性和可行性。

本文所提出的动态搜索半径果蝇优化算法是以搜索半径分段变化的方式来实现算法全局寻优性能和局部寻优性能的均衡。如何寻求一种符合“起始变化率较小而后期变化率较大”的特性函数，有效地实现全局与局部寻优的均衡，这也将是下一步研究的一个重点；同时将DSR-FOA算法与其他方法结合(如SVM等)用于解决某些科学工程问题也是一个较好的研究方向。

[1] WenTsao Pan.A new Fruit Fly Optimization Algorithm:Taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26:69-74.

[2] 潘文超.果蝇最佳化演算法-最新演化式计算技术[M].台湾:沧海书局,2011.

[3] Lin Wang,Yuanlong Shi,Shan Liu.An improved fruit fly optimization algorithm and its application to joint replenishment problems[J].Expert Systems with Applications,2015,42 (9):4310-4323.

[4] Junqing Li,Quanke Pan,Kun Mao,et al.Solving the steelmaking casting problem using an effective fruit fly optimisation algorithm[J].Knowledge-Based Systems,2014,72:28-36.

[5] Mousavi S M,Alikar N,Niaki S T A.An improved fruit fly optimization algorithm to solve the homogeneous fuzzy series-parallel redundancy allocation problem under discount strategies[J].Soft Computing,2016,20(6):2281-2307.

[6] 宁剑平,王冰,李洪儒,等.递减步长果蝇优化算法及应用[J].深圳大学学报:理工版,2014,31(4):367-373.

[7] QuanKe Pan,HongYan Sang,JunHua Duan,et al.An improved fruit fly optimization algorithm for continuous function optimization problems[J].Knowledge-Based Systems,2014,62:69-83.

[8] 张勇,夏树发,唐冬生.果蝇优化算法对多峰函数求解性能的仿真研究[J].暨南大学学报：自然科学与医学版,2014,35(1):82-87.

[9] WenTsao Pan.Using modified fruit fly optimisation algorithm to perform the function test and case studies[J].Connection Science,2013,25(2-3):151-160.

[10] 贺智明,宋建国,梅宏标.结合元胞自动机的果蝇优化算法[J].计算机应用,2014,34(8):2295-2298,2321.

[11] Ling Wang,Xiaolong Zheng,Shengyao Wang.A novel binary fruit fly optimization algorithm for solving the multidimensional knapsack problem[J].Knowledge-Based Systems,2013,48:17-23.

FRUIT FLY OPTIMIZATION ALGORITHM WITH DYNAMIC SEARCH RADIUS

Gao Leifu Zhao Shijie*Tu Jun Yu Dongmei

(Institute of Optimization and Decision,Liaoning Technical University,Fuxin 123000,Liaoning,China)

Considering the problems that the fixed-scale search radius in conventional fruit fly optimisation algorithm (FOA) causes weak local optimisation performance in algorithm’s later-stage and slow convergence,we propose a fruit fly optimisation algorithm with dynamic search radius (DSR-FOA).In its early-stage the algorithm ensures global optimisation performance by a greater search radius,while in later-stage its radius declines dynamically along with the iterations increasing for having better local optimisation performance.This improvement achieves the equilibrium between global and local optimisations effectively.Moreover,in light of the problem of conventional FOA that it is unsuitable for the interval setting of optimised variables,we present an effectual interval-set method which is based on the techniques including setting initial search radius and translation transformation.Numerical experimental results show that the DSR-FOA algorithm has better optimisation precision and smaller prediction standard deviation,which verifies the effectiveness and feasibility of the improved algorithm.

Fruit fly optimisation algorithm Search radius Translation transformation Benchmark testing function

2015-08-10。教育部高等学校博士学科点专项科研基金联合项目(20132121110009);辽宁省教育厅基金项目(L2015208)。高雷阜，教授，主研领域：最优化理论与应用。赵世杰，博士生。徒君，讲师。于冬梅，博士生。

TP18

A

10.3969/j.issn.1000-386x.2016.11.052