基于最短路径的加权属性图聚类算法研究

张素智 张 琳 曲旭凯

(郑州轻工业学院计算机与通信工程学院 河南 郑州 450002)



基于最短路径的加权属性图聚类算法研究

张素智 张 琳 曲旭凯

(郑州轻工业学院计算机与通信工程学院 河南 郑州 450002)

图在计算机领域是一种重要的数据结构，可以用来描述事物之间的复杂关系。图的节点和边具备一个或者多个不同的属性。如何结合属性对图进行聚类是目前所面临的一个新的挑战。目前的属性图聚类算法，多存在聚类效果差，消耗资源多，效率低等缺点。针对以上问题，提出一种基于最短距离的加权属性图聚类算法WASP(weighted attribute graph clustering algorithm based on shortest path)，建立加权属性无向图模型，在此模型上基于最短路径算法度量节点间的关联度，以此为原则选取新的聚类中心对图进行聚类。实验表明，新的聚类算法具有更高效的聚类效果。

图 加权属性图 最短路径 聚类

0 引 言

近年来，图结构被广泛应用于多个领域来描述数据之间的复杂结构。针对海量图数据的分析和挖掘越来越重要。作为图数据挖掘算法的一种，图聚类算法引起了众多关注[1，2]。图聚类，简单描述就是根据图结构上节点和边的某种相似性，将图上的节点和边划分为不同的组。属性图聚类是图聚类中的一种特殊情况，即在用节点和边表示实体和实体关系的同时，还需要考虑到节点和边的属性。在属性图聚类时，同时考虑节点间结构和属性的相似性，则能够得到更加准确的聚类效果。如何更好地同时结合结构和属性进行聚类是目前图聚类研究的热点和难点。

针对属性图聚类问题，现阶段也有许多研究成果：Tian等人[3]根据聚类中节点和属性相一致的原则，提出了k-SNAP算法，该算法通过用户的下钻和上取，将属性一致的点聚集在一起，实现了多粒度的图聚类。但是此算法仅根据节点属性聚类，会造成聚类结构分散，聚类效果中节点数过多。针对k-SNAP算法存在的问题，Zhang等人[4]改进了该算法，对数值属性分类，并对属性相近对按相似度基于最大恶化程度进行划分。Nevile 等人[5]将具有相同属性的属性个数定义为边的权重值，并以此为基础将属性图转化为带权图进行聚类。Steinhaeuser等[6]提出了相似的算法，并将属性扩展到具有连续值域的情况。此类算法由人工定义权重值，虽然算法效率高，但聚类效果和可拓展性差。也有一些算法通过增广属性图[7，8]，采用熵的统一模型来衡量图中的同质性，实现属性图的聚类。该方法虽然将图的结构和属性结合起来聚类，但统一聚类超结点中的结点联系并不紧密。还有一些算法把模型的思想[9，10]应用到属性图聚类中，将属性图聚类转化为概率问题，但此类算法需要事先设定好聚类数量，才能达到较好的聚类效果。

针对以上算法的问题，本文提出了一种基于最短路径的加权属性图聚类算法WASP。该算法通过建立加权属性图模型，对图中边和节点的属性设置权值，确定节点相似度，采用最短路径算法计算节点间的距离，确定聚类中心，并在聚类过程中自动更新权重值，以此为基础进行聚类。最后将WASP算法应用在DBLP数据集中，通过实验对比，该算法具有较好的聚类效果。

1 相关定义

1.1 属性加权无向图定义

定义1属性加权无向图G=(V,E,A,ω)；其中：

V表示属性图中节点集合：V={v1,v2,…,vn}；

E表示属性图中边的集合：E={(vi,vj)|(vi,vj)∈R,1≤i,j≤n,i≠j}；

A表示图的属性的集合：A={a1,a2,…,am}；其中|A|=m′；

ω为边的权重值：ω={ω1,ω2,…，ωp} ，|ω|=p′ ，ωa(ik)表示节点vi的属性ak的权值，若任意两节点vi、vj直接相连，则这两点节点间的权重值为ωi,j= ωq，q∈{1,2…，p}；

1.2 节点相似度定义

在社交网络中，如果用户之间的公共朋友越多，则用户之间的联系越大。对于属性图中的节点，如果节点之间联系的公共节点越多，则这些节点位于同一个簇的可能性越大。本文考虑将与节点直接关联的点称为该节点的节点朋友。

定义2属性图G=(V,E),v为图中的节点。定义节点朋友集合为Κ(v)：

K(v)={u∈V|(v,u)∈E}∪{v}

(1)

若v、u之间有边，即∈E,则将边的相似度定义为：

(2)

2 算法描述

2.1 自动更新属性权重值

为了得到较好的聚类效果，提出了一种自动更新属性权重值的方法，在聚类过程中不断更新属性权重值，来得到较好的聚类效果。

(3)

因此更新后的权重值：

(4)

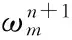
2.2 最短路径算法

为了发现图中高关联度的边，考虑到边的权重和相似度，设定参数α、β，且α+β=1。任意一条边上的关联度为：

(5)

两个节点间路径越长，则关联度越小，若要取得最大关联度的节点，则相邻节点直接取节点间最短距离，非相邻节点取节点之间最短距离的和。最大关联度的和为:

(6)

其中，Z是节点va、ub中间节点的集合。本文采用最短路径算法中的经典算法Dijkstra算法。

根据最短路径的最优子结构性质，如果存在一条从i到j的最短路径(vi,…,vk,vj)，vk是vj前面的一顶点，那么(vi，…，vk)也必定是从i到j的最短路径。为了求出最短路径，Dijkstra提出了以最短路径长度递增，逐次生成最短路径的算法。例如对于源顶点v0，首先选择其直接相邻的顶点中长度最短的顶点vi，那么当前已知可得从v0到达vj顶点的最短距离：

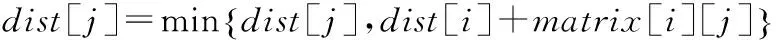
(7)

根据这种思路，假设存在图G=(V,E,ω)，源顶点为v0，U={v0},dist[i]记录v0到vi的最短距离，path[i]记录从v0到vi路径上的i前面的一个顶点，则算法过程为：

1) 从{V-U}中选择使dist[i]值最小的顶点i，将i加入到U中；

2) 更新与i直接相邻顶点的dist值，即dist[j]=min{dist[j],dist[i]+matrix[i][j]}；

3) 直到U=V。

2.3 聚类算法描述

基于最短路径的图聚类算法，就是在计算最大关联度时采用最短路径算法，选取相应的节点并划分到同一簇中。具体算法步骤如下：

输入：属性加权无向图G=(V,E,A,ω)，初始权重值ω=1.0，聚类数量k，参数α=0.4，β=0.6；

输出：划分的不同的簇；

1) 计算边的相似度Γ(v,u)；

2) 在初始聚类数量k中选择节点作为初始聚类中心Vstart，且Vstart不能为空集。定义剩余节点Vleft=V-Vstart；

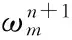
4) 在划分好的节点中，根据更新的权重值，得到L(va,ub)，并将关联度大且距离短的的节点划分为一簇；

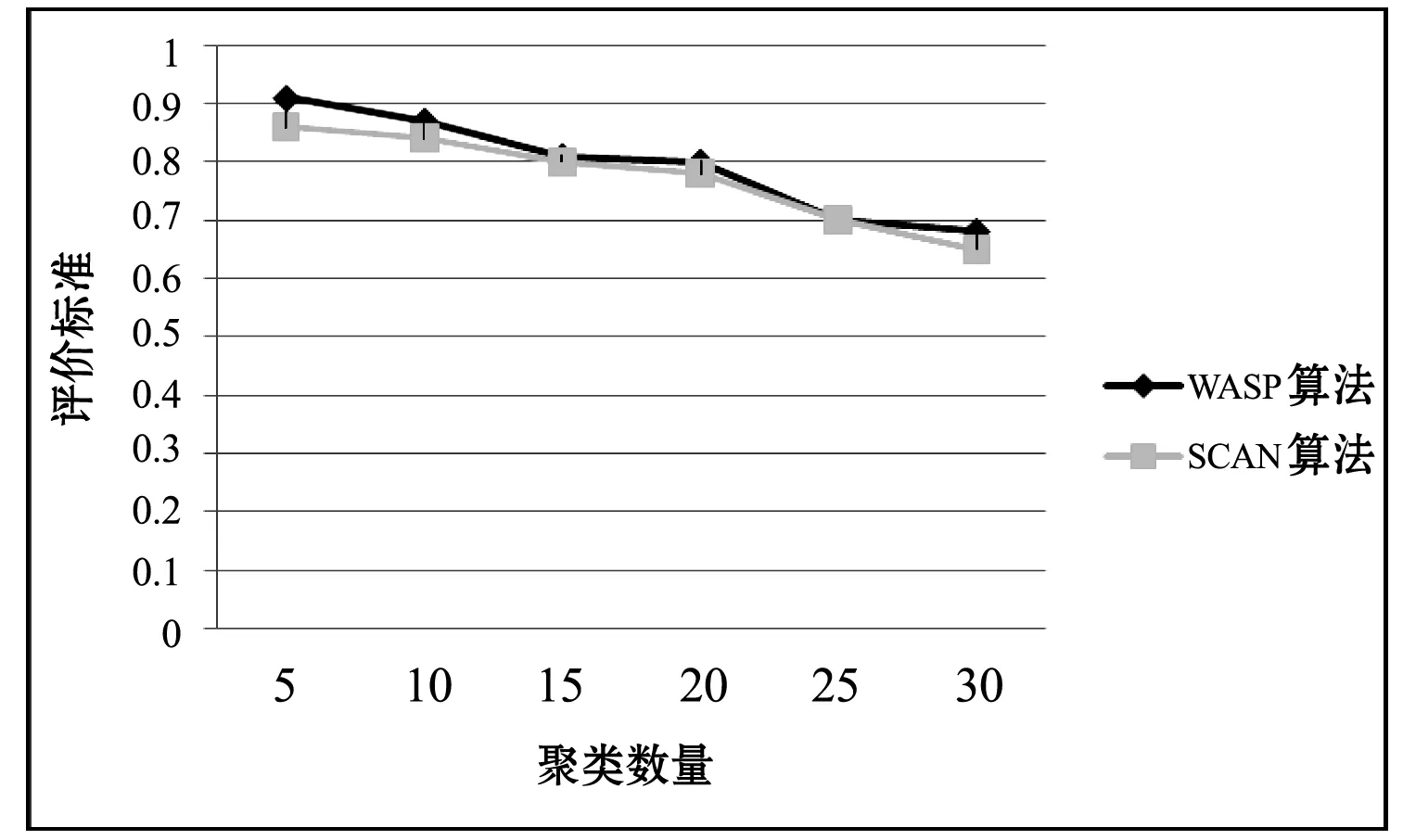
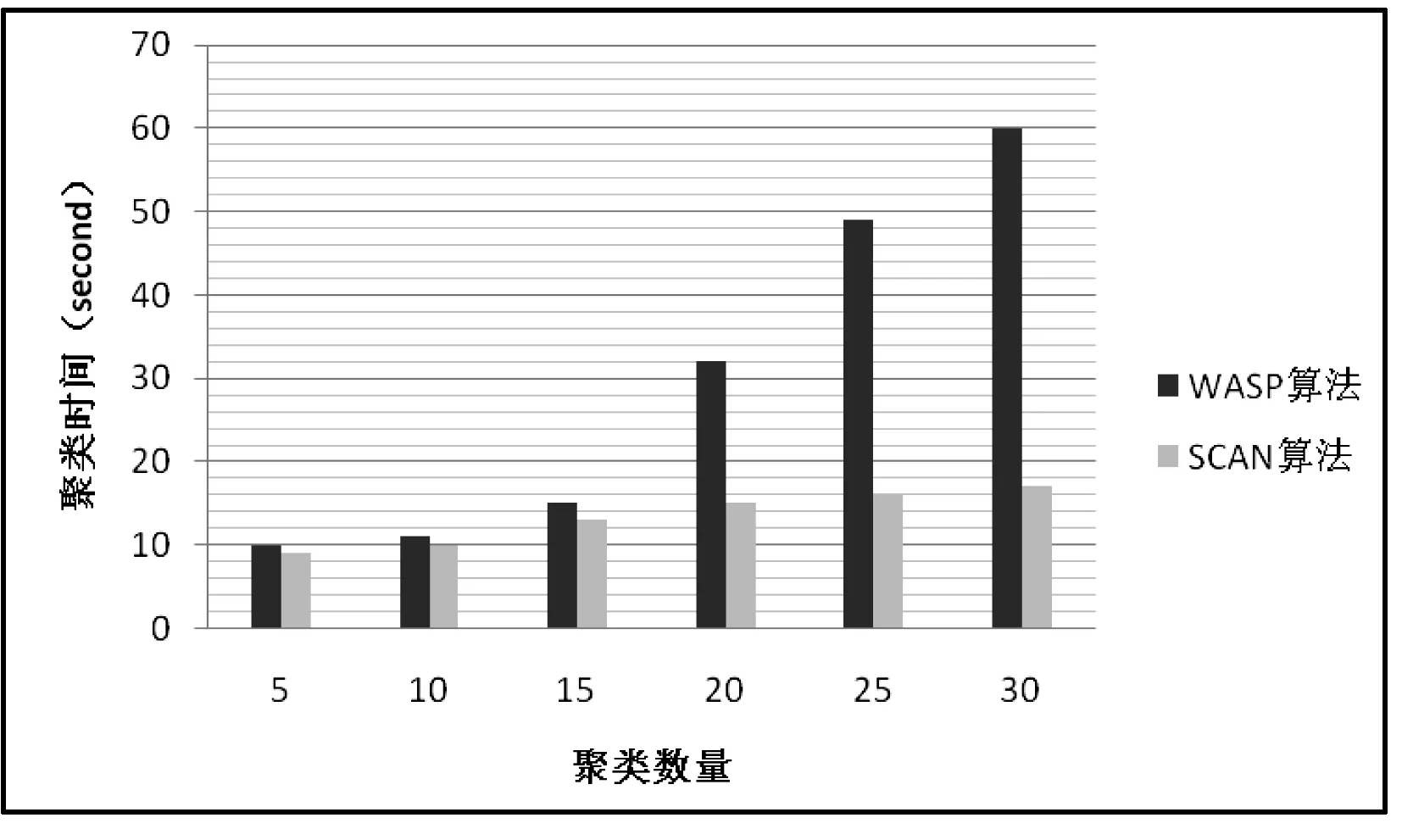
5) 若Vleft=∅，则聚类结束，所有节点划分完毕，若Vleft≠∅且Vleft

WASP算法是一种基于最短路径对图的结构和属性聚类的算法。在算法时间复杂度方面，第1步，计算边的相似度，时间复杂度为Ο(n)；第2、3步，选择聚类中心的，时间复杂度为Ο(n3)，第3-5步，计算最短路径，划分节点到不同的簇，时间复杂度为Ο(kn-n2)，其中k为初始聚类数量。该算法总体时间复杂度为Ο(n3)。

3 实验与分析

3.1 实验数据集

本次实验采用DBLP数据集。这是一个学术合作关系的网络。由德国的特里尔大学创建的发表在计算机期刊、杂志和会议论文的数据库系统。该网络包括一万多个节点和两万多条无向边。其中节点表示论文作者，边代表作者们合作完成的论文。本次实验选择了该网络提供的在数据挖掘、数据库、人工智能、信息检索等相关领域发表论文最多的5000名作者英文单位。

作者单位的中英文要完全对应，每个实词的首字母大写。在部门名称和单位名称之间、在单位名称和城市名之间使用英文逗号隔开，城市名和邮编之间使用一个英文空格隔开，不能用逗号。

3.2 评价标准

(8)

3.3 实验结果

实验时设定聚类初始数量k=5,10,15,20,25,30，图1为WASP算法与SCAN算法在DBLP数据集上的聚类密度效果。由图1可知，在聚类数量较少时，WASP算法与SCAN算法聚类效果没有太大差别，但当聚类数量增多时，WASP算法更具有优势。这是因为WASP算法不但考虑了图的属性和结构，还考虑到了节点间的权重值，在聚类数量增多的时候，节点间的权重值也会增大，此时WASP算法聚类效果更明显。

图1 聚类密度结果图

为了更好地对比两个算法的聚类效率，选择对比两算法的聚类时间。在实验数据集上分别运行WASP算法和SCAN算法各10次，并记录下每次运算所消耗的时间。取10次运算的平均值作为聚类时间。

由图2可知，当聚类数目较小时，WASP算法与SCAN算法聚类时间差距不大。但当聚类数目开始增多时，SCAN算法无明显变化，WASP算法却出现变化。这是因为由于该算法在聚类迭代时，每次都要计算当前聚类中心到所有节点的最短距离。当聚类数量增多，即k的值增加时，由于算法3-5步的时间复杂度为Ο(kn-n2)，算法第3-5步所消耗的时间将会增加。因此算法总体时间将会变长，而对于SCAN算法来说，时间复杂度不会有明显变化。在大型图聚类算法中，WASP算法时间会长于SCAN算法，但由于k值对WASP算法时间影响较小，因此具体到实际应用中只有几秒钟时间，且在小型数目集中没有明显区别。

图2 聚类时间图

4 结 语

本文通过对现有图聚类算法的研究，以加权属性图为模型，提出了基于最短路径的加权属性图算法。该算法结合图的属性和结构进行聚类，实验表明，该算法比一般图聚类算法具有更好的聚类效果。但是该算法在大型图上聚类时间略长于其他聚类算法，需要在今后的工作中进一步的改进。

[1] Majumdar D,Kanjilal A,Bhattacharya S.Separation of scattered concerns: a graph based approach for aspect mining[J].ACM SIGSOFT Software Engineering Notes,2011,36(2): 1-11.

[2] Sengupta S,Kanjilal A,Bhattacharya S.Measuring complexity of component based architecture: a graph based approach[J].ACM SIGSOFT Software Engineering Notes,2011,36(1): 1-10.

[3] Tian Y,Hankins R A,Patel J M.Efficient aggregation for graph summarization[C]//Proceedings of the 2008 ACM SIGMOD international conference on Management of data.ACM,2008: 567-580.

[4] Zhang N,Tian Y,Patel J M.Discovery-driven graph summarization[C]//Data Engineering (ICDE),2010 IEEE 26th International Conference on.IEEE,2010: 880-891.

[5] Neville J,Adler M,Jensen D.Clustering relational data using attribute and link information[C]//Proceedings of the text mining and link analysis workshop,18th international joint conference on artificial intelligence.2003: 9-15.

[6] Steinhaeuser K,Chawla N V.Community detection in a large real-world social network[M]//Social computing,behavioral modeling,and prediction.Springer US,2008: 168-175.

[7] Cheng H,Zhou Y,Yu J X.Clustering large attributed graphs: A balance between structural and attribute similarities[J].ACM Transactions on Knowledge Discovery from Data (TKDD),2011,5(2): 12.

[8] Liu Z,Yu J X,Cheng H.Approximate homogeneous graph summarization[J].Information and Media Technologies,2012,7(1): 32-43.

[9] Xu Z,Ke Y,Wang Y,et al.A model-based approach to attributed graph clustering[C]//Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data.ACM,2012: 505-516.

[10] Zanghi H,Volant S,Ambroise C.Clustering based on random graph model embedding vertex features[J].Pattern Recognition Letters,2010,31(9): 830-836.

[11] Zhou Y,Cheng H,Yu J X.Clustering large attributed graphs: An efficient incremental approach[C]//Data Mining (ICDM),2010 IEEE 10th International Conference on.IEEE,2010: 689-698.

STUDY ON SHORTEST PATH-BASED CLUSTERING ALGORITHM OF WEIGHTED ATTRIBUTE GRAPH

Zhang Suzhi Zhang Lin Qu Xukai

(School of Computer and Communication Engineering,Zhengzhou University of Light Industry,Zhengzhou 450002,Henan,China)

Graph is an important data structure in computer science,and can be used to describe the complex relationship between things.The nodes and edges in graph have one or more different attributes.How to cluster the graph in combination with attributes is a new challenge encountered at present.Many of current attribute graph clustering algorithms have the drawbacks of poor clustering effect,big resource consumption and low efficiency.In view of the above problems,this paper puts forward a shortest path-based weighted attribute graph clustering algorithm,and builds the weighted attribute undirected graph model.Based on the model the algorithm measures the correlation degree between the nodes based on shortest path algorithm,and takes this as the principle to select new clustering centre to cluster the graph.Experiment shows that the new clustering algorithm has more efficient clustering effect.

Graph Weighted attribute graph Shortest path Clustering

2015-06-10。国家自然科学基金青年科学基金项目(61201447)。张素智，教授，主研领域：Web数据库，分布式计算，异构系统集成。张琳，硕士生。曲旭凯，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2016.11.050