基于网格服务的电力海量数据分布式恢复算法
2016-12-26周爱华朱韵攸朱力鹏
常 涛 周爱华 朱韵攸 朱力鹏 饶 玮 邓 松
1(国网重庆市电力公司 重庆 400014)2(国网智能电网研究院 江苏 南京 210003)3(国网重庆市电力公司信息通信分公司 重庆 401121)4(南京邮电大学先进技术研究院 江苏 南京 210023)
基于网格服务的电力海量数据分布式恢复算法
常 涛1周爱华2*朱韵攸3朱力鹏2饶 玮2邓 松4
1(国网重庆市电力公司 重庆 400014)2(国网智能电网研究院 江苏 南京 210003)3(国网重庆市电力公司信息通信分公司 重庆 401121)4(南京邮电大学先进技术研究院 江苏 南京 210023)
传统的基于纠错码的数据恢复算法既提高了数据存储的可靠性,又增加了数据恢复的计算时间。为了解决这个问题,首先对整个样本数据采用粗糙集进行约简,然后基于网格服务思想,提出基于网格服务的电力海量数据分布式恢复算法DR-GSPMD(Distributed Recovery based on Grid Service for Power Mass Data)。仿真实验表明针对所有测试数据集,随着校验码个数的增加,整个系统的最大容错率和数据恢复时间也随着增加。同时针对约简后的数据集随着计算节点数的增加,算法降低了计算复杂度,加快了范德蒙矩阵运算的速度,减少了整个数据恢复的时间。
数据恢复 网格服务 属性约简
0 引 言
随着云计算、物联网等新型信息通信技术在智能电网中的不断深入应用,智能电网发电、输电、变电、配电、用电及调度等各个环节的业务系统数据呈几何级数增长[1,2]。如何保证这些数据存储的安全可靠性是需要解决的一个重要问题。为了解决这个问题,各类分布式存储系统应运而生。这些基于分布式环境的存储系统最终目标就是要使得用户能连续且高可靠地访问存储数据,尤其是当存储数据被外部攻击或者损坏时,业务系统仍能正常运行,保证用户的最大服务质量,这对智能电网业务系统运行,特别是与外部因特网环境直接连接的业务系统至关重要。
副本技术[3-6]就是一种通过创建数据的完整或者部分的备份,然后分布式存储在各个网络节点中的一种技术。这种技术具有提高数据访问效率(可以就近访问)、增强数据可用性、改善数据冗余性等优势。左方等提出一种基于蚁群算法的云存储副本动态选择算法,实现了副本的有效分发和虚拟机集群的负载均衡[7]。针对服务质量比较敏感的用户,文献[8]提出一种基于QoS 偏好感知的副本选择策略。李功丽等提出一种云计算数据副本动态管理策略[9],通过基于用户需求来确定副本数目以此确定副本的位置,降低平均响应时间。
但现有电力行业中的数据由于采集手段和采样频率的多样化,各业务系统所包含的数据集大部分都是比较庞大的,维度较高,完全复制会带来相当高的带宽和存储空间需求。在不考虑存储经济性的前提下,直接利用数据完全副本进行数据恢复的前提是该副本本身是完整可靠的,为了解决这个问题,很多研究者借鉴了信号处理领域的冗余容错技术[10-12],提出利用Erasure编码来解决数据恢复问题,但是随着数据量的呈几何级数增加以及数据的高维特征,直接利用Erasure code进行编码和解码将耗费大量的计算时间,从而大大影响了整个数据恢复的时间,最终会影响到对实时性要求较高的电力业务系统运行。因此,本文针对电力海量数据安全存储的实际需求,为了提高Erasure Code的编码和解码速度,结合属性约简和网格服务的思想,提出了基于网格服务的电力海量数据分布式恢复算法DR-GSPMD。
1 基于属性约简和Erasure Code的数据恢复算法
Erasure Code是一种典型的纠错码技术[10],具有良好的容错性和安全性。它的实现形式有很多类型,由于基于范德蒙矩阵的编码简单、易实现等特点,本文重点研究该RS编码中基于范德蒙矩阵的数据恢复技术。首先给出相关的概念[10]。
定义1对于n块子数据块和m个校验块,构造如下的矩阵:
(1)
则称式(1)为范德蒙矩阵,其中ai,i∈[1,n]可以为任意自然数。
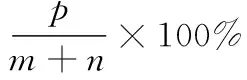
但随着云计算、物联网在智能电网中的广泛应用,越来越多的智能电网业务系统数据维度越来越高,数据量越来越大,使得在分布式存储过程中直接基于Erasure Code进行数据恢复的时间复杂度过大,从而影响后台业务系统所提供的服务质量。为了更快地基于Erasure Code进行数据恢复,首先需要对电力高维海量数据进行属性降维,其方法主要包括主成份分析方法,奇异值分解法,以及粗糙集等。前两种方法不可避免地会造成原始数据信息的部分丢失,而基于粗糙集的属性约简在降维的同时,并没有改变约简后数据的决策规则。因此本文提出基于粗糙集和Erasure Code的数据恢复算法DR-RSEC(Data Recovery algorithm based on Rough Set and Erasure Code),首先利用粗糙集对待恢复的海量高维数据进行属性约简,降低其数据自身复杂度,然后再通过Erasure Code进行数据恢复计算,这样在不改变数据本身决策能力的前提下,提高数据恢复的效率。
在介绍DR-RSEC算法之前,首先给出相关基于粗糙集的属性约简的定义[13]。
定义3样本决策表SDT。设T=
定义4对于∀P⊆R,且x,y∈U,当且仅当对于∀r∈P,f(x,r)=f(y,r)时,x和y是不可分辨的,也即:IND(P)={(x,y)∈U|∀r∈P,f(x,r)=f(y,r)}。
定义5设样本决策表T=
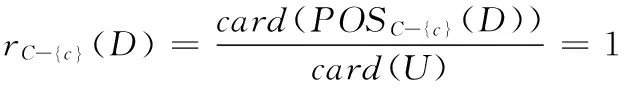
整个基于粗糙集和Erasure Code的数据恢复算法DR-RSEC的形式化描述如算法1所示。
算法1DR-RSEC
Input: 原始数据集Odata,n个数据块,校验码个数m;
Output: 恢复后的数据RData;
Begin
1. 针对原始数据集Odata,构造样本决策表T=
2. for (c∈C) {
3. if (rC-{c}(D)=1)C=C-{c};}
4. 得到约简后的T=
5. 将约简后的样本数据集分割为n块;
6. 根据分割块数n和校验码个数m,分别构造范得蒙矩阵Fm×n以及分割后的数据矩阵Dn×1;
7. 校验码矩阵Cm×1=Fm×n×Dn×1;
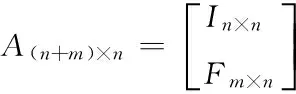
9. if (n块数据子块中有p块受损) {
10. if (p<=m) {
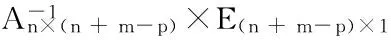
12. RData==Merger(Dn×1);}
13. else {print (“不可恢复!”)}
14. Return RData.
算法1的时间复杂度为O(n(m+n)+|U||C|),主要集中在属性约简和矩阵运算中。随着数据量和数据维度的增大,以及分割块数和校验码个数的增加,整个算法的时间复杂度将会急剧增加,这势必将影响到数据恢复的时间。
2 基于网格服务的电力海量数据分布式恢复算法
2.1 算法思想
为了解决传统的Erasure code的海量计算的问题,本文在算法1的基础上,结合网格服务的思想,提出了基于网格服务的电力海量数据分布式恢复算法DR-GSPMD。通过网格服务,来构造并行分布式计算平台,大大减少了计算的时间,提高了数据恢复的效率。
DR-GSPMD算法的主要思想就是首先利用粗糙集对原始数据集进行属性约简;然后根据分割块数和校验码个数来分别构造范得蒙矩阵、分割后的数据矩阵以及计算恢复所需的其他矩阵,接着把按照行对每一个矩阵进行分解,然后把分解后的各个子矩阵分别传输到各个网格节点中;其次编写相关矩阵的乘运算以及求逆运算的网格服务,并把该网格服务部署到相应的服务端;然户分别把相应矩阵运算网格服务所需的参数通过数据传输服务传输到指定的服务端;最后客户端通过门户并行地调用和执行各网格服务,并把处理后的最终结果返回给客户端。
2.2 算法描述
基于网格服务的分布式数据恢复算法主要就是把数据恢复中的有关矩阵运算进行分解,然后利用网格服务来并行化处理这些计算,从而提高计算的效率。整个算法的描述如下所示:
算法2基于网格服务的电力海量数据分布式恢复算法DR-GSPMD
Input: 原始数据集Odata,n个数据块,校验码个数m;
Output: 恢复后的数据RData;
Begin {
1. 客户端首先根据原始数据集,基于粗糙集进行属性约简,求解得到约简后的待分割数据集;
2. 基于约简后的待分割数据集,根据分割块数和校验码个数,分别构造范得蒙矩阵Fm×n以及分割后的数据矩阵Dn×1;
3. 根据部署矩阵乘算法网格服务的节点个数,分解Fm×n和Dn×1,然后把分解后的各个子矩阵分别传送到各个算法服务的节点上;
4. 对于每一个网格服务节点,并行进行矩阵相乘,最后传输到客户端进行合并成校验码矩阵Cm×1;
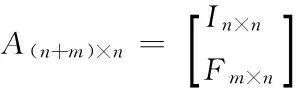
6. if (n块数据子块中有p块受损) {
7. if (p<=m) {
8. 将p个数据子块对应的矩阵A(n+m)×n和E(n+m)×1中的行删除掉,得到新的矩阵A(n+m-p)×n和E(n+m-p)×1;
11. 对于每一个网格服务节点,并行进行矩阵相乘,最后传输到客户端进行合并成数据矩阵Dn×1;
12. RData=Merger (Dn×1);}
13. Return RData;
算法2的通信开销主要集中在各个网格节点之间传输数据子矩阵、各个矩阵相乘的耗时,同时由于对各个矩阵分解后利用网格服务进行并行运算,故整个算法的时间复杂度大大减少。整个恢复过程是利用矩阵乘算法服务以及矩阵求逆算法服务协同工作,大大提高了矩阵求解的效率,节约了数据恢复的时间。
3 实验与分析
为了证明DR-GSPMD算法的有效性,本文在实验室环境下做了仿真实验分析。整个实验平台为P4 1.8 GHz+512 MB+Java+Windows XP+WS-Core 4.0.2,所有的程序由Java语言实现。其中包括5台计算节点,每个节点配置为2×E5-2620v2 CPU,128 GB内存以及2×4 TB硬盘。为了说明算法的有效性,本文的数据源主要包括随机产生大小分别为100 MB、500 MB、1 GB和50G的三个数据集和来自国家电网公司某业务系统2006年-2012年的网络安全日志数据约1.5 GB。整个实验数据的属性如表1所示。
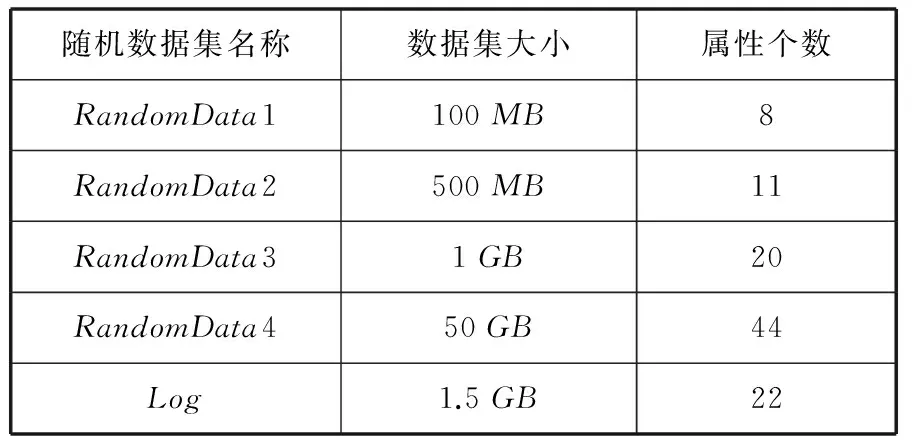
表1 实验数据集
实验1针对表1中所示的实验数据集,表2给出了属性约简后的各个数据集的属性个数。图1给出了当数据分割块数固定时,随着产生校验码个数的增加,数据集最大容错率的变化情况。图2则给出了当数据块数为5,随着校验码个数的增加,上述5个数据集约简前的恢复算法的计算耗时的变化情况。图3给出了当数据分割块数为5,校验码个数为3时,约简前后的数据恢复算法的计算耗时比较。
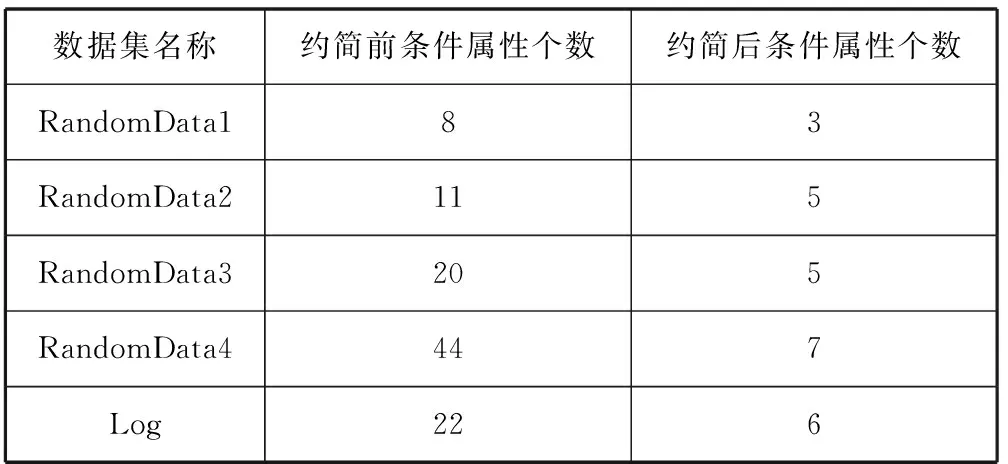
表2 基于粗糙集的数据集属性约简前后条件属性个数变化
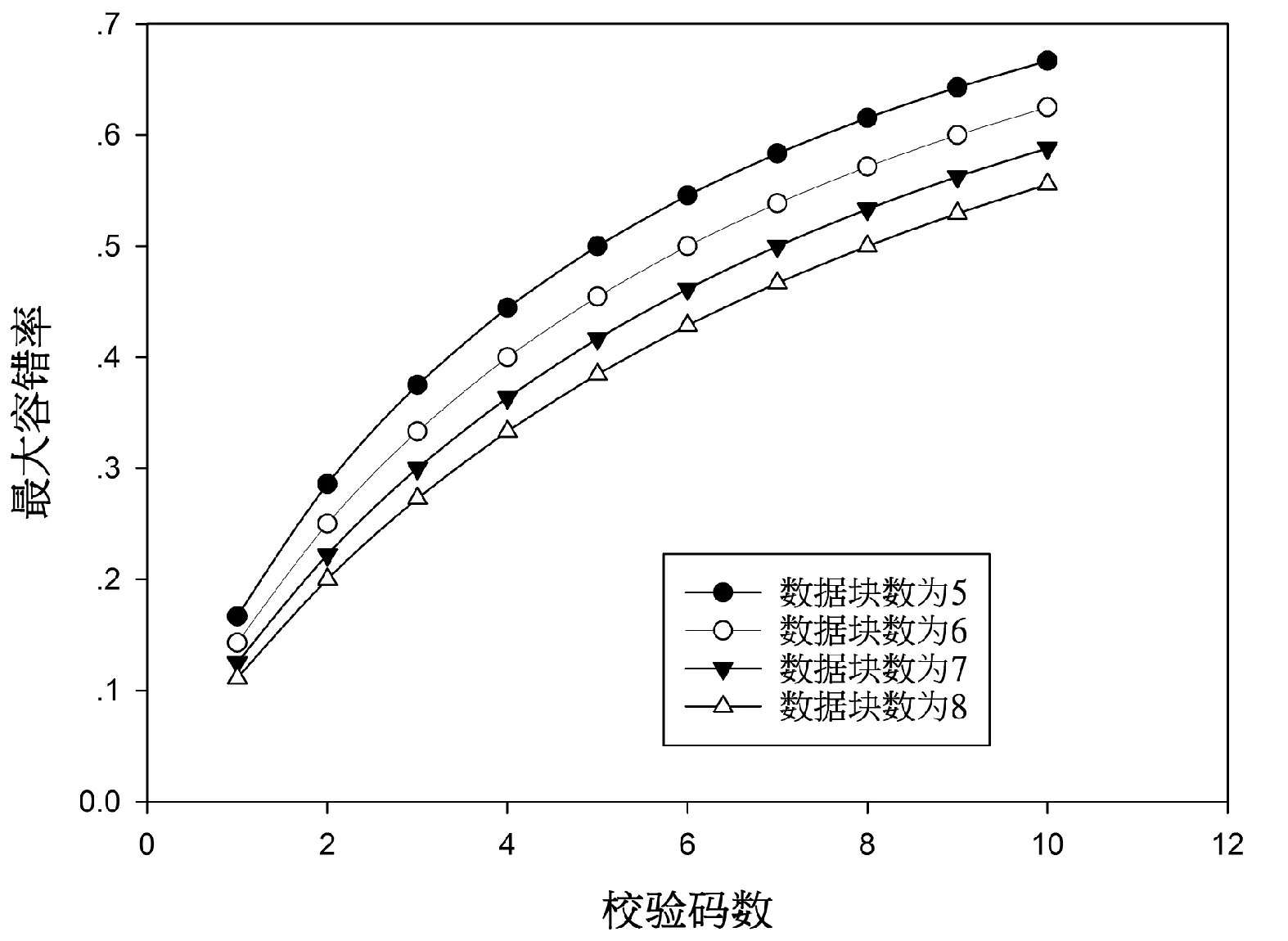
图1 不同数据块条件下最大容错率随着校验码数变化的情况
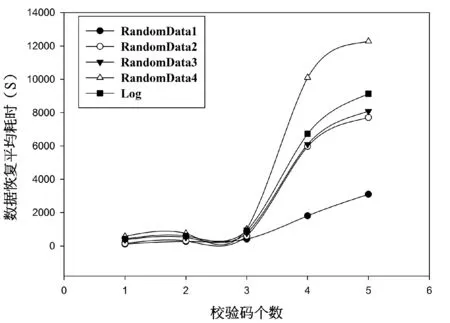
图2 不同校验码个数条件下五个数据集的数据恢复算法耗时
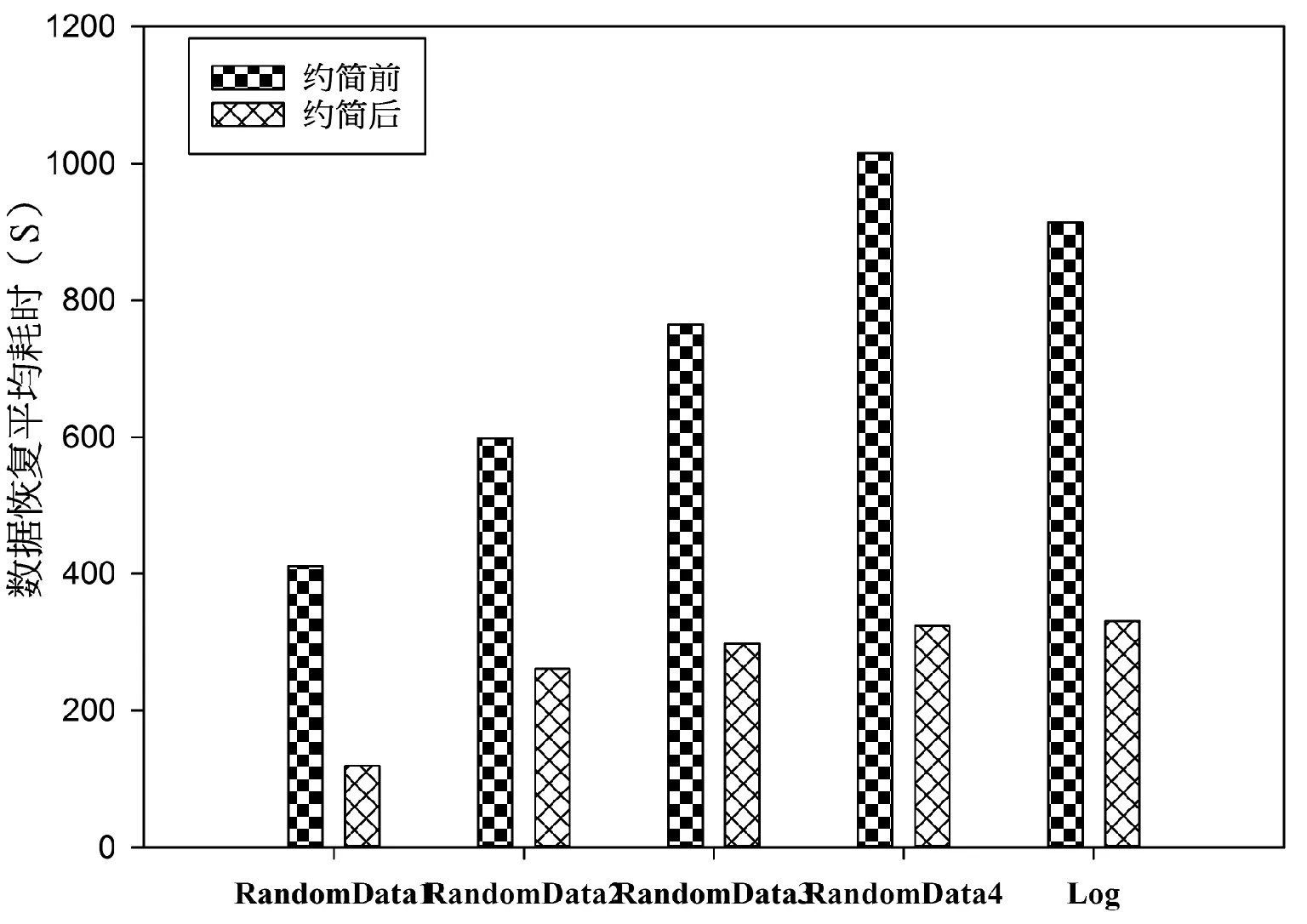
图3 约简前后的数据恢复算法的计算耗时比较
从表2中可以看出针对表1中的5个测试数据集而言,约简后的条件属性个数分别下降了62.5%、54.55%、75%、84.09%、72.73%。从图1中可以看出,随着校验码个数的增加,整个系统的最大容错率也随着增加,而最大容错率的增加表明了整个恢复系统的可靠性增加,允许有更多的数据子块的丢失。而图2则表明当数据块数为5时,随着校验码个数的增加,表1中五个数据集的数据恢复算法平均计算耗时分别增加了27.42、51.07、21.93、21.17、21.81倍。这是因为随着校验码个数和数据集大小的增加,构造的范得蒙矩阵、数据矩阵以及校验码矩阵的复杂度也随之增加,从而使得整个算法花费大量的时间在矩阵的运算中。图3则显示当数据分割块数为5,校验码个数为3时,通过对表1中所示的五个数据集进行属性约简,大大降低了表1中五个数据集恢复算法的计算耗时。
实验2由实验1可以看出,较多的校验码个数可以保证数据存储的高可靠性,但同时也增加了数据恢复的计算耗时。为了很好地解决这个问题,实验2利用网格服务设计并行数据恢复算法DR-GSPMD,在保证数据存储高可靠性的同时,也极大地降低了数据恢复的时间。图4表明了当分割块数n=5,校验码个数m=4时,随着节点数目的增加,数据恢复的计算耗时变化情况。
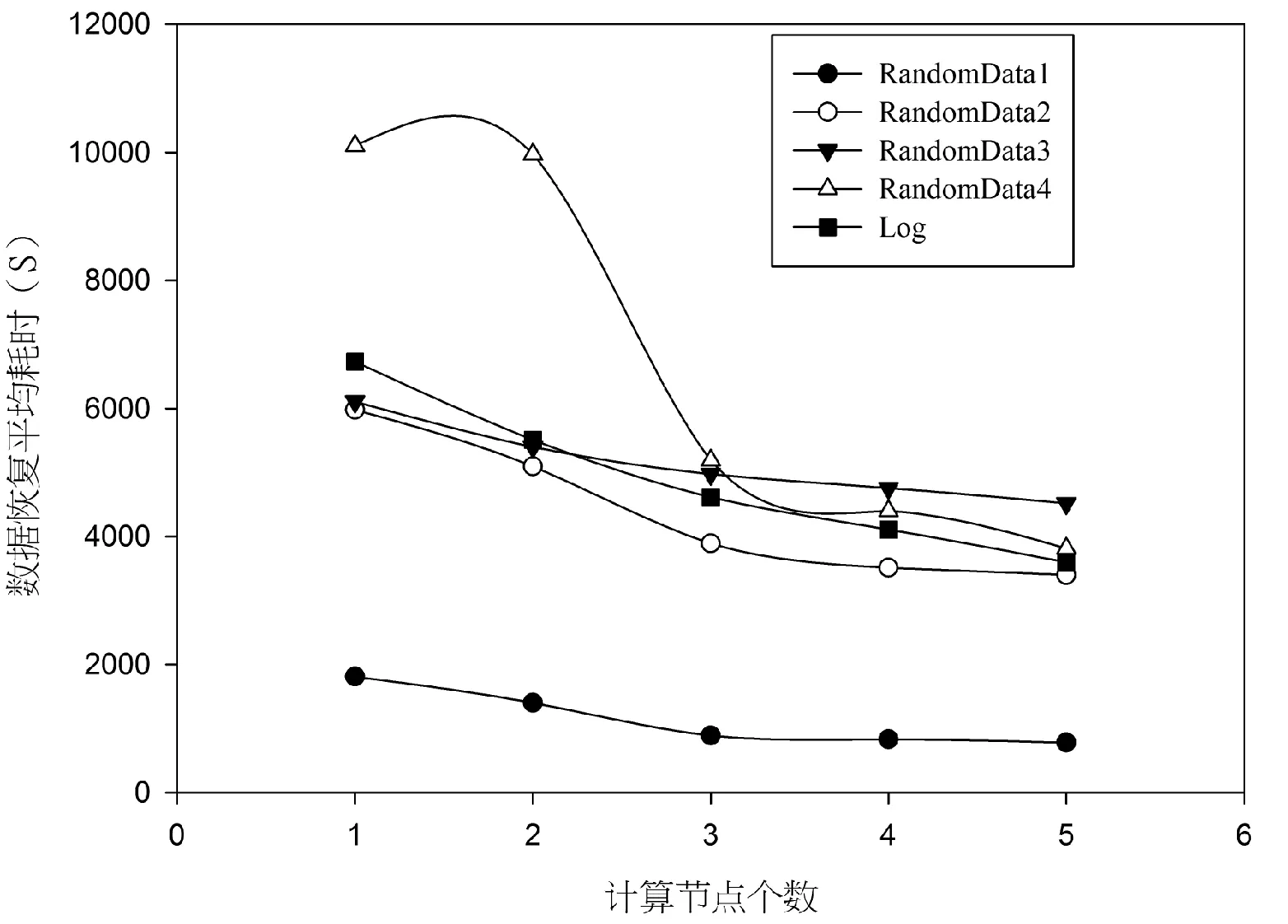
图4 不同计算节点个数条件下5个数据集恢复的平均耗时
从图4中可以看出,在分割块数为5,校验码个数为4的条件下,随着计算节点的增加,五个随机数据集的平均恢复时间分别最大降低56.88%、43.19%、26.08%、62.28%、46.58%。这主要是因为在分割块数和校验码个数确定的情况下,恢复所有的计算都集中在矩阵的乘法和求逆运算,而DR-GSPMD算法利用网格服务使得矩阵的乘法和求逆计算并行化,加快了整个矩阵的运算,最终导致整个恢复时间的下降。
4 结 语
本文在传统基于Erasure code的数据恢复算法基础上,结合网格服务和属性约简的思想,提出了基于网格服务的电力海量数据分布式恢复算法DR-GSPMD。首先利用属性约简降低原始数据维度从而减少数据恢复算法的计算耗时;同时对于数据恢复算法中的大量的矩阵乘法和求逆运算,DR-GSPMD设计了相应的网格服务,使得数据恢复中的各种矩阵运算并行化。仿真实验表明,随着节点的增加,DR-GSPMD算法加快了矩阵计算的速度,减少了整个数据恢复的时间。
[1] 秦立军, 马其燕. 智能配电网及其关键技术[M].北京:中国电力出版社, 2010.
[2] Nouredine Hadjsaid.有源智能配电网[M].陶顺, 肖湘宁, 彭骋,译.北京:中国电力出版社, 2013.
[3] Ranganathan K, Foster I. Identifying Dynamic Replication Strategies for a High Performance Data Grid[C]//Proceeding of the Second International workshop on Grid Computing, Denver, November, 2001:75-86.
[4] 杨涛.数据网络中复制管理研究[D].北京:中国科学技术大学,2007.
[5] Rahman R M, Alhajj R, Barker K. Replica selection strategies in data grid[J].Journal of Parallel and Distributed Computing, 2008,68(12):1561-1574.
[6] Al Mistarihi H H E, Yong C H. On fairness, optimizing replica selection in data grids[J].IEEE Transactions on Parallel and Distributed Systems, 2009,20(8):1102-1111.
[7] 左方, 何欣. 一种基于蚁群算法的云存储副本动态选择机制研究[J].计算机应用研究,2015,32(11):3368-3370,3374.
[8] 熊润群, 罗军舟, 宋爱波,等.云计算环境下QoS偏好感知的副本选择策略[J]. 通信学报, 2011,32(7):93-102.
[9] 李功丽, 赵晓焱, 刘慧.一种云计算数据副本动态管理策略[J].河南师范大学学报:自然科学版,2015, 43(4):138-143.
[10] 罗象宏, 舒继武.存储系统中的纠删码研究综述[J].计算机研究与发展, 2012,49(1):1-11.
[11] 毛波, 叶阁焰, 蓝琰佳,等.一种基于重复数据删除技术的云中云存储系统[J].计算机研究与发展,2015,52(6):1278-1287.
[12] 潘利伟,谷建华,朱靖飞,等.基于Erasure Code 的分布式文件存储系统[J].计算机工程,2010,36(17):45-47.
[13] Pawlak Z. Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
DISTRIBUTED RECOVERY ALGORITHM FOR MASSIVE POWER DATA BASED ON GRID SERVICE
Chang Tao1Zhou Aihua2*Zhu Yunyou3Zhu Lipeng2Rao Wei2Deng Song4
1(State Grid Chongqing Electric Power Company, Chongqing 400014, China)2(State Grid Smart Grid Research Institute, Nanjing 210003,Jiangsu, China)3(State Grid Chongqing Information and Telecommunication Company, Chongqing 401121, China)4(Nanjing University of Posts and Telecommunications, Nanjing 210023,Jiangsu, China)
Traditional error-correcting code-based data recovery algorithm improves the reliability of data storage but increases the computational time of data recovery as well. To solve this problem, we first employed the rough set to carry out reduction on entire sample data, and then proposed the grid service-based distributed recovery algorithm for massive power data (DR-GSPMD), which is based on the idea of grid services. Simulation experiments showed that for all test datasets, the maximum error rate and data recovery time of whole system increases along with the augment in numbers of check node. Meanwhile, aiming at the problem that the reduced datasets increases along with the augment in numbers of computational nodes, DR-GSPMD reduces the computing complexity, speeds up the calculation of Vandermonde matrix and decreases the time of entire data recovery.
Data recovery Grid service Attribution reduction
2015-09-24。国家自然科学基金项目(51507084)。常涛,高工,主研领域:电力信息化。周爱华,工程师。朱韵攸,工程师。朱力鹏,工程师。饶玮,工程师。邓松,高工。
TP3
A
10.3969/j.issn.1000-386x.2016.11.047
