基于最小包络矩形的不规则凸多边形的三角形处理算法
2016-12-26王淑青张子蓬袁晓辉
王淑青 陈 军 潘 健 张子蓬 袁晓辉 何 莉
1(湖北工业大学电气与电子工程学院 湖北 武汉 430068)2(湖北工业大学计算机学院 湖北 武汉 430068)3(华中科技大学水电与数字化工程学院 湖北 武汉 430074)
基于最小包络矩形的不规则凸多边形的三角形处理算法
王淑青1陈 军1潘 健1张子蓬2袁晓辉3何 莉1
1(湖北工业大学电气与电子工程学院 湖北 武汉 430068)2(湖北工业大学计算机学院 湖北 武汉 430068)3(华中科技大学水电与数字化工程学院 湖北 武汉 430074)
针对最小矩形包络算法处理不规则多边形时包络率低并造成板材使用率低的现象,在最小矩形包络算法基础上,提出三角形处理法。通过包络求解、分类、组合三个环节将不规则凸多边形转化成矩形,并采用遗传算法及最低水平轮廓算法进行矩形排样。通过对比实验,验证了三角形处理算法提高板材使用率的有效性。
三角形处理算法 最小包络矩形 矩形排样 遗传算法
0 引 言
自动排样技术在建筑、航空等各工业领域中广泛应用。不规则多边形由于形状与大小相对复杂,其排样过程比规则多边形困难许多,因而成为学者们重点研究方向。常见思路有以下几种:1)临界多边形法NFP,此方法能有效解决不规则多边形排样问题,但其计算复杂,效率较低[1,3];2)碰撞算法,该算法通常求解时间比较长,且不容易产生最优解[2,5];3)转化为规则图形[3-5]。
为了简化不规则的排样,工业上通常会把不规则多边形转化成矩形,然后进行矩形排样,通常使用最小矩形包络算法[4]。该算法具有操作简单方便、复杂度低的优点,其缺点在于包络时会产生大量空白区域,造成板材的浪费[5]。文献[6]在最小矩形包络算法基础上研究了多边形两两组合的算法,该方法能有效提高板材利用率,但比较复杂,计算量较大。少量文献研究了圆形件的排样,如文献[7]采用了圆形包络算法与矩形排样相结合,但并不能有效提高板材使用率。
本文针对最小矩形包络算法的缺点,在此基础上提出三角形处理算法对不规则凸多边形进行预处理,从而到达既简化排样又提高板材利用率的目的;并采用遗传算法及最低水平轮廓布局算法进行矩形排样。
1 最小矩形包络算法
能够将不规则图形所有点和线全部包围的矩形称为包络矩形。每个不规则多边形有无穷多个包络矩形,其中面积最小的称为最小包络矩形[3]。
假定某凸多边形的边按逆时针排列依次为l1,l2,…,li,…,ln,其最小矩形包络算法步骤如下:
Step1 选择凸多边形一条边li,计算此边与x轴的夹角;
Step2 利用坐标转换公式,旋转凸多边形,使li与x轴平行;
Step3 利用式(1)计算旋转后各顶点的坐标,找出xmin、xmax、ymin、ymax;
Step4 利用式(2)计算包络矩阵长L、宽W以及面积S。
重复Step1-Step4,直至遍历完凸多边形每一条边,得到n个包络矩形,并选择面积最小的作为最小包络矩形。
x′=x+d-d×cosθ
(1)
y′=y-d×sinθ
(2)
其中,(x,y)为坐标转换前各点坐标,(x′,y′)为坐标转换后各点坐标。d为坐标转换前各点到旋转中心点(x0,y0)的距离。
L=xmax-xmin
(3)
W=ymax-ymin
(4)
S=WL
(5)
最小矩形包络算法优点是操作简单、时间复杂度低、易于实现,但缺点在于待排样图形的面积与包络矩形的面积之比较小,排样图形之间空隙大,造成板材浪费。
2 三角形处理算法
2.1 三角形处理算法
为了简便排样同时又提高板材利用率,本文在最小包络矩形基础上提出了三角形处理算法。该算法主要包括四个环节:包络图形求解、包络方法的选择、包络三角形的分类、同类三角形的组合。流程如图1所示。
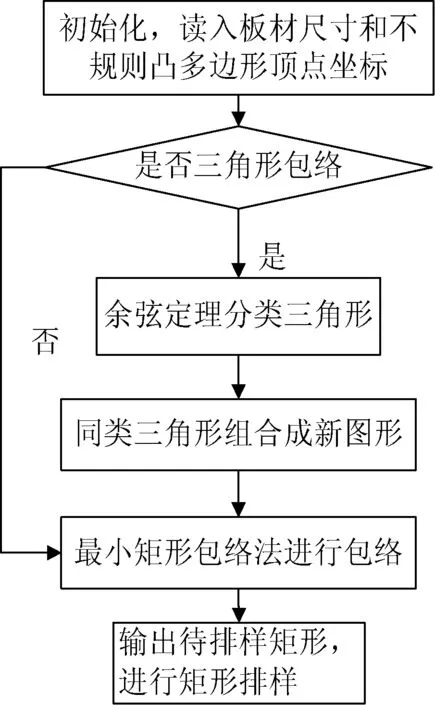
图1 三角形处理算法流程图
三角形处理后得到的矩形,将进行矩形排样。该过程将采用遗传算法和最低水平轮廓布局算法对所有转换成矩形的凸多边形整体排样。
2.2 包络三角形的求解
包络图形面积较大是最小矩形包络算法造成材料浪费的主要原因。本文提出了使用三角形包络不规则凸多边形的方法,使包络图形面积更小。
假定某个多边形有n个顶点,其坐标按逆时针排列依次为(x1,y1),(x2,y2),…,(xn,yn),边分为l1,l2,…,li,…,ln。其三角形包络的步骤如下:
Step1 计算不规则多边形顶点个数n,若n>3,跳至下步骤,若n=3,包络三角形已经生成,停止于此步骤;
Step2 求得不规则多边形的最短边li,将此边相邻的两条边li-1,li+1延长,相交于一点P,则P将成为包络三角形的一个顶点,同时删除最短边。重复Step1-Step2。
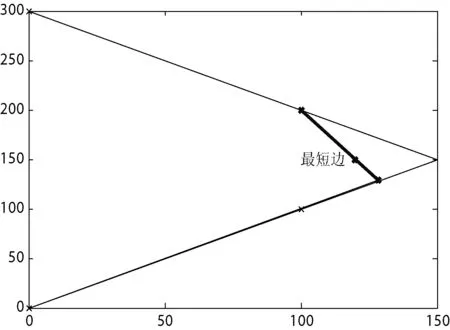
图2 三角形包络效果图
实验证明,只有一大部分不规则凸多边形,三角形包络算法比最小矩形包络算法的包络图形面积更小。因此,对于每一个不规则凸多边形,本文将分别使用最小矩形包络算法与三角形包络算法包络该凸多边形,计算包络矩形面积Sa与包络三角形面积Sb。若Sa>Sb,则该凸多边形使用最小矩形包络算法;若Sa 2.3 余弦向量分类三角形 为了大小及形状相似的包络三角形以最简单方式组合拼接成新图形进行排样,将采用余弦向量法对包络三角形进行分类。包络三角形的特征向量表示形式如下: (6) 其中: (7) (8) (9) (10) 其中,c1、c2、c3分别表示包络三角形最长边、次长边、最短边。 定义1特征向量相似度:用来衡量两个特征向量的相似度,本文选取为两条射线之间夹角余弦值[8]。 (11) P值越大,两个特征向量夹角就越小,方向就越一致,特征向量相似度越大,两个包络三角形之间形状大小差异也就越小。当P>0时,说明两个包络三角形形状大小有相似之处;当P<0时,说明两个包络三角形之间形状大小差异性较大[8]。 在使用余弦定理求解之前,对所有包络三角形特征向量组成的矩阵进行归一化处理。求解结果表明,选取分类阈值为0.9时分类效果比较好。 2.4 同类三角形的组合 在所有包络三角形分类之后,本文提出一种简单易操作组合方式,将这些大小形状相同的三角形组合成新图形,并将新图形包络成最小矩形用于矩形排样。以下为同类三角形组合的具体步骤: Step1 找出同一类别中每个包络三角形最短边、次短边、最长边,并分别求出这些最短边的最大值c1、次短边最大值c2、最长边最大值c3。 Step2 用(c1,c2,c3)三条边组成的三角形包络这一类别中所有不规则凸多边形。 Step3 用对头双排方式组合,将大小形状相同的三角形使用翻转拼接在一起,组合成新图形。组合后的图形将是三角形、梯形、平行四边形三种图形其中一种。 Step4 将组合后的新图形包络成最小矩形,用于同直接使用最小矩形包络算法得到的矩形一起进行矩形排样。 不规则多边形经过处理转化成矩形后,对其进行矩形排样。矩形排样需考虑“矩形排样定序”和“矩形排放布局”两个问题。本文分别采用“遗传算法”[9-12]和“最低水平轮廓算法”[11]解决这两个问题。其算法流程如图3所示。 图3 矩形排样流程图 (1) 编码 假设有标号为1~n的待排样矩形,将标号1~n按照随机顺序组合成一个序列,序列中每个数字的正负号随机生成。 (2) 解码 本文采用最低水平轮廓线算法对染色体中每一个基因代表的矩形进行排样。每一个待排图形,先找出能放下该图形的轮廓,再在这些轮廓中挑选最下最左的轮廓。若是没有长度大于待排矩形宽的轮廓,则90°旋转待排矩形,用旋转前的方法选择适合的轮廓线排放。如果90°旋转后也没有适合轮廓,则将矩形放置于板材未排区域最左最下处。 (3) 适应度函数 对于底边长度一定的矩形板材,排样区域高度越小,则说明排样效果越好。故取适应度函数为: (12) (4) 选择 适应度越高的编码,排样效果越好,越应该选择遗传到下一代。本文采用赌轮盘的方法选择存留几率大的染色体编码,不经过变异、组合操作,直接保存至下一代染色体。 (5) 变异 对于赌轮盘选择操作中淘汰的染色体,将进行染色体变异的进化行为。随机产生两个[0,1]的数字P1和P2,若P1>pb1,则随机选择染色体中的两个数字,并将两个数字间的数字倒置,逆序放置;若P2>pb2,则改变基因的正负号。其中pb1、pb2为变异算子。 (6) 交叉 随机产生一个[0,1]的数字P3,若P3>pc,则随机选择赌轮盘中两个淘汰的染色体,取其相同部分基因进行交换。如果交换后有重复数字,则使用重复数字的对应位数字进行调整,直到没有重复数字。如染色体1234与染色体4312第2~3位交叉后为1312与4232,调整后的子代为2314与4231,其中pc为交叉算子。 4.1 凸多边形矩形包络和三角形包络对比 使用MATLAB 7.0实现算法,随机选取了十个凸多边形,分别采用最小矩形包络和三角形包络,得到两种包络方法的占有率,实验数据如表1所示。 表1 矩形包络与三角形包络对比数据 由表1可以看出,部分凸多边形包络三角形比最小包络矩形面积小,从而比最小矩形包络更节省材料;但是形状接近平行四边形的凸多边形使用最小矩形包络法(如编号2、6、ee8样本)的包络图形面积更小。 因此本文对每个待排样凸多边形分别进行最小矩形包络和三角形包络,算出两种方法的包络图形面积,然后选择包络图形面积小的方法进行包络和处理。 4.2 整体排样结果比较 为了检验三角形处理算法的效果,本文采用遗传算法和最低水平轮廓算法进行矩形排样,分别使用三角形处理算法和最小矩形包络算法将不规则凸多边形转换成矩形。 本文采用实验样本是如表1所示随机产生的10种不规则凸多边形,每种多边形个数如表2所示。 表2 矩形排样样本 图4与图5分别为使用最小矩形包络算法处理后得到的矩形排样效果图以及适应度函数值变化曲线图。图6与图7分别为使用三角形处理算法后得到的矩形排样效果图以及适应度函数值变化曲线图。 三角形处理法组合环节中,会将同一类的几个三角形拼接组合后,再进行最小矩形包络。因此,实验样本经过三角形算法处理的矩形(如图4所示)和直接经过最小包络矩形算法处理的矩形(如图6所示)并不相同。三角形处理算法得到的矩形个数更少,面积更大。 图4 矩形算法排样效果 图5 矩形排样适应度函数 图6 三角形算法排样效果 图7 三角形排样适应度函数 由图4至图7可以看出,宽度为400单位长度的板材,三角形处理算法处理后的矩形排样板材使用高度为260单位长度,最小矩形排样算法处理后矩形排样板材使用高度为280单位长度。三角形处理算法的板材使用面积是最小矩形包络算法的91%,这在工业上将节约大量的成本。三角形处理算法能在最小矩形包络算法基础上提高板材使用率。 最小矩形包络算法处理不规则多边形简单易操作,但待排样图形包络率低,从而造成板材浪费。本文提出三角形处理算法,将待排样不规则凸多边形有选择性地进行三角形包络,分类组合成新图形,再使用最小矩形包络算法包络。结合遗传算法和最低水平轮廓算法进行矩形排样,在最小矩形包络算法基础上使板材利用率提高。后期还可以对凹多边形的三角形包络以及三角形分类时特征向量选择进行研究。 [1] 杨卫波,王万良.改进临界多边形生成算法[J].计算机工程与应用,2013,49(1):32-35. [2] 梁利东,钟相强.碰靠定位算法在不规则件排样优化中的应用研究[J].中国机械工程,2013,24(23):3191-3195. [3] 郭怡,李辉.基于蚁群算法的矩形件排样问题研究[J].中国农机化学报,2014,35(4):250-252,256. [4] 陈小雨.二维不规则零件自动优化排样算法的研究[D].哈尔滨:哈尔滨理工大学,2012. [5] 程晖.基于遗传模拟退火的服装排料算法的研究[D].上海:东华大学,2012. [6] Elkeran A.A new approach for sheet nesting problem using guided cuckoo search and pairwise clustering[J].European Journal of Operational Research,2013,231(3):757-769. [7] 梅颖.船体建造板材套料系统中排样优化算法与碰靠技术研究[D].广州:华南理工大学,2010. [8] 吴军.数学之美[M].北京:人民邮电出版社,2012. [9] 郭瑞峰.基于病毒进化遗传算法的二维不规则图形排样[D].广州:广东工业大学,2014. [10] 刘璐.基于遗传算法的钣金排样系统研究[D].西安:西安工业大学,2014. [11] 王淑青,雷蕾,曾仕琦,等.基于改进遗传算法的二维图形优化排样方法[J].工业控制计算机,2012,25(12):51-53. [12] 吴忻生,吴超成,刘海明.基于改进遗传算法的矩形件排样优化算法[J].制造业自动化,2013,35(10):55-58,115. [13] Domovic D,Rolich T,Grundler D,et al.Algorithms for 2D nesting problem based on the no-fit polygon[C]//Information and Communication Technology,Electronics and Microelectronics (MIPRO),2014 37th International Convention on.IEEE,2014:1094-1099. A TRIANGLE PROCESSING ALGORITHM FOR IRREGULAR CONVEX POLYGON BASED ON SMALLEST ENVELOPE RECTANGLE Wang Shuqing1Chen Jun1Pan Jian1Zhang Zipeng2Yuan Xiaohui3He Li1 1(School of Electrical and Electronic Engineering,Hubei University of Technology,Wuhan 430068,Hubei,China)2(School of Computer,Hubei University of Technology,Wuhan 430068,Hubei,China)3(School of Hydropower and Information Engineering,Huazhong University of Science and Technology,Wuhan 430074,Hubei,China) When dealing with irregular polygons,the smallest rectangle envelope algorithm has low envelopment rate,this causes low sheet utilisation rate.To solve the problem,this paper puts forward the triangular processing algorithm based on the smallest rectangle envelope method,it converts irregular convex polygon into a rectangle through three links of envelope calculation,classification and composition.Moreover,it uses genetic algorithm and minimum-level horizontal contour algorithm to operate rectangular layout.Contrast experimental results verify the effectiveness of the proposed algorithm in increasing the sheet utilisation rate. Triangular processing algorithm Smallest envelope rectangle Rectangular layout Genetic algorithm 2015-06-02。国家自然科学基金项目(51379080,51309094,61473116)。王淑青,教授,主研领域:智能控制,系统建模。陈军,硕士生。潘健,副教授。张子蓬,副教授。袁晓辉,教授。何莉,副教授。 TP3 A 10.3969/j.issn.1000-386x.2016.11.0463 矩形排样

4 实验结果


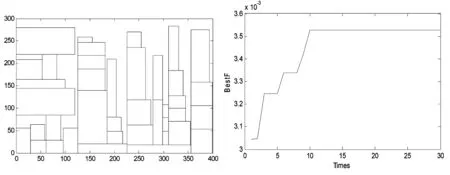
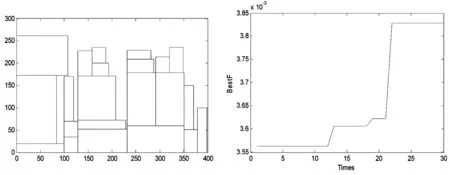
5 结 语
