应用混沌烟花算法求解置换流水车间问题

曹 磊 叶春明 黄 霞

(上海理工大学管理学院 上海 200093)



应用混沌烟花算法求解置换流水车间问题

曹 磊 叶春明 黄 霞

(上海理工大学管理学院 上海 200093)

改进烟花算法求解置换流水车间问题。用最大位置法编码，将连续变量映射到离散空间。引入动态半径因子，平衡局部搜索与全局搜索。精英个体混沌搜索,进一步挖掘个体信息。用锦标赛策略替代原有的选择算子，群体中的优良个体被选择的概率增大。通过正交实验选择合适参数，求解Car类和Rec类基准问题。与基本烟花算法、萤火虫算法和粒子群算法的对比实验说明，改进后的混沌烟花算法在寻优率、寻优速度等上具有一定的优势，是求解置换流水车间问题的有效工具。

烟花算法 混沌搜索 置换流水车间问题

0 引 言

置换流水车间问题是许多实际生产系统的抽象模型，属于组合优化问题。现已证明3台以上的置换流水车间问题为NP-Hard问题[1]。因此，对于此类问题的求解具有一定的理论与实际价值。

解决此类问题的方法一般有：精确算法、启发式算法、智能算法等。精确算法在理论上可以求得问题最优解，但是耗时较长。启发式算法能较快地找到问题的近似最优解，但是求解精度较差。智能算法是如今发展较快寻优方法，它能在较短的时间内寻得问题最优解或近似最优解。

烟花算法FWA(fireworks algorithm)是一种新颖的群智能算法，是由Tan等人于2010年根据烟花爆炸产生火花这一自然现象提出的[2]。FWA自提出后被应用于许多领域的优化问题，主要应用领域有参数优化[3]、配电网重构优化[4]、滤波器设计[5]、图像识别[6]、施肥问题[7]等。从现有研究来看，将烟花算法应用于生产调度的文章暂时未有。

很多智能算法易于陷入局部最优，选取合适的方法使搜索跳出局部极值是改进算法的有效手段。混沌是一种较为普遍的现象，它指系统中看似无序，类似随机的现象。混沌具有随机性、遍历性、规律性等特点。李兵[8]首先利用此现象提出混沌优化算法。由于混沌算法的随机性及遍历性等特点，其具有跳出局部极值的能力，更易于达到全局最优。自提出之后，混沌优化算法得到了广泛应用[9-11]。

在分析基本烟花算法的基础上，本文将混沌搜索策略运用到烟花寻优的过程中。通过引入逻辑自映射函数产生混沌序列，对每一代中的精英个体进行混沌搜索，挖掘精英个体的信息。并通过应用动态半径因子、锦标赛选择策略进一步加强改进烟花算法在置换流水调度问题中的寻优性能。

1 混沌烟花算法

1.1 烟花算法

受烟花爆炸启发，谭营提出了烟花算法[1,12]。在烟花算法中，每个烟花可看成一可行解，爆炸产生火花的过程可视为邻域搜索寻优的过程。烟花算法中存在这样的机制：适应度差的烟花爆炸半径较大，使其具有全局搜索能力；而适应度好的烟花爆炸半径较小，使其具备局部搜索能力。这与实际烟花爆炸机理是吻合的。一般而言，好的烟花是多而密，差的烟花是少而稀。在烟花算法中存在两种形式的火花，即爆炸火花和高斯变异火花。爆炸火花为烟花在其邻近区域内产生的火花，可视为烟花的子代，用于搜寻邻域内更优解。而高斯变异火花的引入增强了种群的多样性，在一定程度上避免了陷入局部最优。

在烟花算法中，爆炸算子、变异算子和选择策略是决定烟花算法性能优劣的要素。

1.1.1 爆炸算子

爆炸火花通过爆炸算子产生。每个火花由特定的烟花产生，并且其位置同样由父代烟花决定。适应度好的烟花产生较多的爆炸火花，火花分布于烟花周围。因此，适应度高的烟花附近聚集较多的火花；适应度低的火花周围分布较少的火花，且火花距离中心烟花较远。对于烟花i子代火花个数Si以及分布半径Ri定义如下：

(1)

(2)

其中：SN为爆炸火花数，A为基本爆炸半径，fi为烟花i的适应度值，ymax为当前烟花种群中的最大适应度值，ymin为当前烟花种群中的最小适应度值，ε为机器最小值，避免除零操作。为了保证每个烟花爆炸而来的火花数为整数，一般对式(1)、式(2)产生的数四舍五入取整。

为了控制较好烟花的火花数不过多，较差烟花的火花数不过少，对烟花i的火花数有如下控制：

(3)

式中，a、b是两个常数，round是根据四舍五入原则的取整函数。根据式(1)、式(2)，由烟花i生成的火花，按照下式进行位置更新：

(4)

若出现超界，通过式(5)将火花映射到有效区域。

(5)

式中，LBk、UBk为解空间在维度k上的上边界和下边界，mod为取余函数。

1.1.2 变异算子

高斯火花由变异算子产生。高斯火花的存在增加了种群的多样性。在烟花种群中随机选择一定数目的烟花，对每一个烟花随机选择一定数目的维度进行高斯变异操作。对于烟花i的某一个维度k执行高斯变异操作为：

(6)

其中有e～N(1,1)，N(1,1)表示均值为1、方差为1的高斯分布。高斯变异火花可能超出可行域的边界范围，通过式(5)将超界火花映射到区域内。

1.1.3 选择策略

在原始烟花算法中，存在这样的选择规则：由烟花、爆炸火花和高斯火花共同组成候选集合K，从集合中选取N个个体作为下一代烟花。除最优个体外，其余N-1个个体均由轮盘赌规则选出，每个个体被选择的概率为：

(7)

式中，dij为第i和j个烟花个体之间的欧式距离，定义如下：

dij=‖xi-xj‖

(8)

从式(7)、式(8)可以看出，在所有个体中，与其他个体总偏离越大的，其被选择的概率越大。此种选择机制避免了群体密集位置被选择概率过大，陷入局部最优，但其并不一定能指引群体向优良方向进化。

1.2 烟花算法性能分析及改进

1.2.1 编码

基本烟花算法优化的是连续问题，而置换流水车间问题需要解决的是工件排序问题，属于离散调度。因此，需要建立连续空间到离散空间的映射。采用最大位置法LOV(Largest Order Value)对烟花及其火花进行编码[13]。烟花位置分量中，最小的数值标记为1，次小的位置分量标记为2，直至所有位置分量被标记。位置分量相同时，规定近左先编码。这样，一个烟花的位置量就映射为唯一的工件加工序列。

1.2.2 选择策略

在原始烟花算法的选择策略中，优良个体不一定被选中，而与群体偏离最多的个体被选择的概率较大。本文采用一种基于适应度大小的锦标赛选择策略，按照一定的组规模(百分比)r选择一定数量的个体作为候选集合J。比较它们的适应度，适应度最大的被选择(同适应度时，序号靠前的优先被选)，重复此操作直到选出N个烟花。伪代码如下：

P={}

for i 1 to N

generate set J and size J= round(r*N)%生成指定规模候选集合J

if f(Xi)=min(f(J))

P=P∪Xi

end if

end for

return P

1.2.3 动态半径因子

根据式(1)，性能优良的烟花会产生较多的爆炸火花。通过式(2)，适应度高的烟花的搜索半径会相对较小。当A设置过小时，每一个烟花的搜索半径均较小，搜索半径具有一定的趋同性，不利于种群的寻优。当A设置较大时，意味着算法寻优步长相对较大，一方面会出现超界现象，产生较多的非可行解；另一方面会降低局部寻优的能力。引入自适应半径因子A(t)，定义如下：

(9)

式(2)可更新为：

(10)

其中，t为当前迭代次数，Ainitial为初始半径，Afinal为最终搜索半径，maxgen为最大迭代次数。迭代初期，种群整体搜索半径相对较大，有利于种群在全局范围寻优。随着迭代次数的增加，烟花会在邻域以较小的搜索半径寻找最优解。因此，自适应半径因子可很好地平衡全局寻优与局部寻优。

1.3 混沌搜索策略

混沌搜索具有随机性、遍历性等特点，在一定程度上可以使烟花算法跳出局部最优。基本思想是将进行混沌搜索的烟花个体通过混沌映射规则对应为混沌搜索空间中的混沌变量，利用混沌变量做遍历性寻优搜索，将遍历到的混沌变量序列转换为解向量序列，找到本次混沌优化得到的最好解向量，来更新混沌搜索之前的烟花个体。

在寻优过程中，为了在运算速度和求解精度之间保持平衡，采用精英奖励策略。对选取的优质个体进行混沌优化搜索，而对于性能相对较差的个体，用随机重新产生的个体代替，保证进化种群的多样性和跳离局部极值的能力。

产生混沌序列的模型很多，本文采用具有更好遍历性的逻辑自映射函数来产生混沌序列[14,15]，表示为：

(11)

在方程中只要迭代初值不为零，混沌就会发生，逻辑自映射函数的定义域为(-1，1)且不为0和0.5。混沌优化的过程为：在搜索过程中的某个时刻，烟花个体xi先按照下式将个体空间位置映射到混沌区域(-1，1)中：

(12)

然后按照式(11)进行混沌遍历搜索得到混沌变量序列，再将获得的混沌变量序列按照式(13)变换到原解空间进行性能评价。

(13)

2 置换流水车间问题及其求解

2.1 置换流水车间问题

置换流水车间调度问题研究n个工件在m台机器上的流水加工过程，每个工件需要m道工序。约定每台机器加工的各工件顺序也相同，每个工件在各机器上加工顺序相同，每个工件在某时刻只能被一台机器加工，每台机器在某时刻只能加工一个工件。已知各工件在各机器上所需的加工时间和准备时间，求使某项生产指标(最小最大完工时间、总流经时间、总拖期时间等)最优的调度方案。 本文寻优目标为最小化完工时间。

假设PN,M表示工件N在机器M上的加工时间(假设各工件的加工准备时间已包含在加工时间PN,M内或为零)，Γ为所有排序的集合，π=(j1,j2,…,jn)表示工件集合的一个排序，π*表示其中最优调度排序；C(ji,k)表示工件ji。

在机器k上的加工时间,π排序的数学描述如下：

C(j1,1)=Pj1,1

(14)

C(ji,1)=C(ji-1,1)+Pji,1

(15)

C(j1,k)=C(j1,k-1)+Pj1,k

(16)

C(ji,k)=max{C(ji,k-1),C(ji-1,k)}+Pji,k

(17)

Cmax(π)=C(jn,m)

(18)

Cmax(π*)=min(Cmax(π)) ∀π∈Γ

(19)

其中，k=2,3,…,m;i=1,2,…,n。

2.2 混沌烟花算法求解置换流水车间问题

通过1.2节、1.3节之于烟花算法的分析，将混沌搜索策略加入到烟花算法寻优过程中。寻优过程如下：

Step1 初始化算法基本参数，包括烟花个数N、基本火花个数SN、高斯火花个数M、基本烟花半径A、上下边界等；

Step2 初始烟花位置：根据ROV规则，将烟花位置转化为工件排序，计算每个烟花的适应度值；

Step3 N个烟花开始爆炸，根据式(1)和式(10)计算火花数目和爆炸半径；

Step4 生成爆炸火花和高斯变异火花；

Step5 根据适应度值，通过锦标赛选择策略，从烟花、爆炸火花、高斯火花中选择N个作为下一代的烟花；

Step6 根据1.3节中混沌搜索策略，对新生成的烟花群体进行混沌搜索，并更新群体；

Step6 判断是否超出最大迭代次数。若否，则进入Step3；若是，则退出循环，输出最优值。

3 参数分析与仿真对比

本文实验环境为：PC计算机处理器主频2.1 GHz，内存2 GB，Windows 7操作系统，MATLAB R2010b编程环境。针对置换流水车间的基准问题Car类和Rec类问题进行参数分析及对比实验。

3.1 参数分析

烟花算法中主要的参数有烟花个数N、基本火花个数SN、变异火花个数M、基本半径A。

对Car3问题，通过正交实验，研究烟花算法参数对问题寻优的影响。建立四因素、三水平正交实验表(L9(34))，如表1、表2所示。每组参数组合独立运行20次，以平均性能AVG作为评价指标，实验结果见表2所示。为分析各参数对算法性能的影响趋势，计算各参数的极差和重要程度，如表3所示。由表3可以看出,参数SN的极差最大,等级最高。这说明，在四个参数中，基本火花数目对算法的寻优性能影响最大。基本火花数目越大，每个烟花对应的爆炸火花越多，这在一定程度上增加了种群的规模。而同样与种群规模有关的参数烟花个数N与变异火花数目M则对算法性能提升相对不明显。而基本烟花半径A对算法寻优性能影响较大，从图1可以直观地看出，A较大或较小均影响算法的寻优性能。A较大使得爆炸火花的搜索半径较大，挖掘局部信息的能力较弱，而较小的A使得算法不易跳出局部极值。因此，A较大或较小均不合适。

表1 参数水平

表2 正交实验表

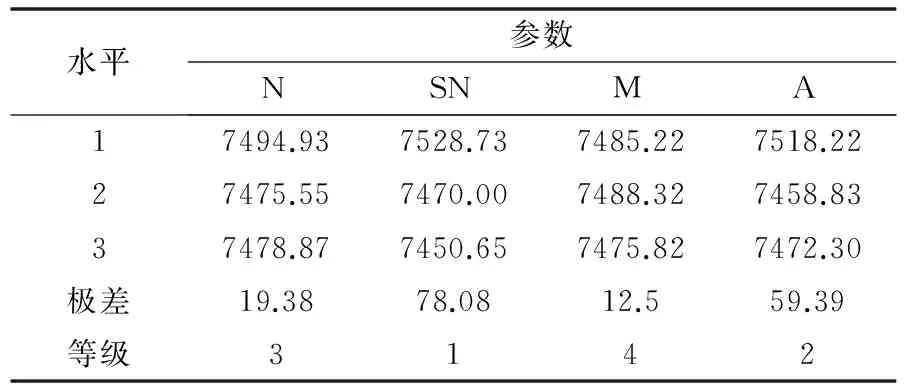
表3 参数性能分析

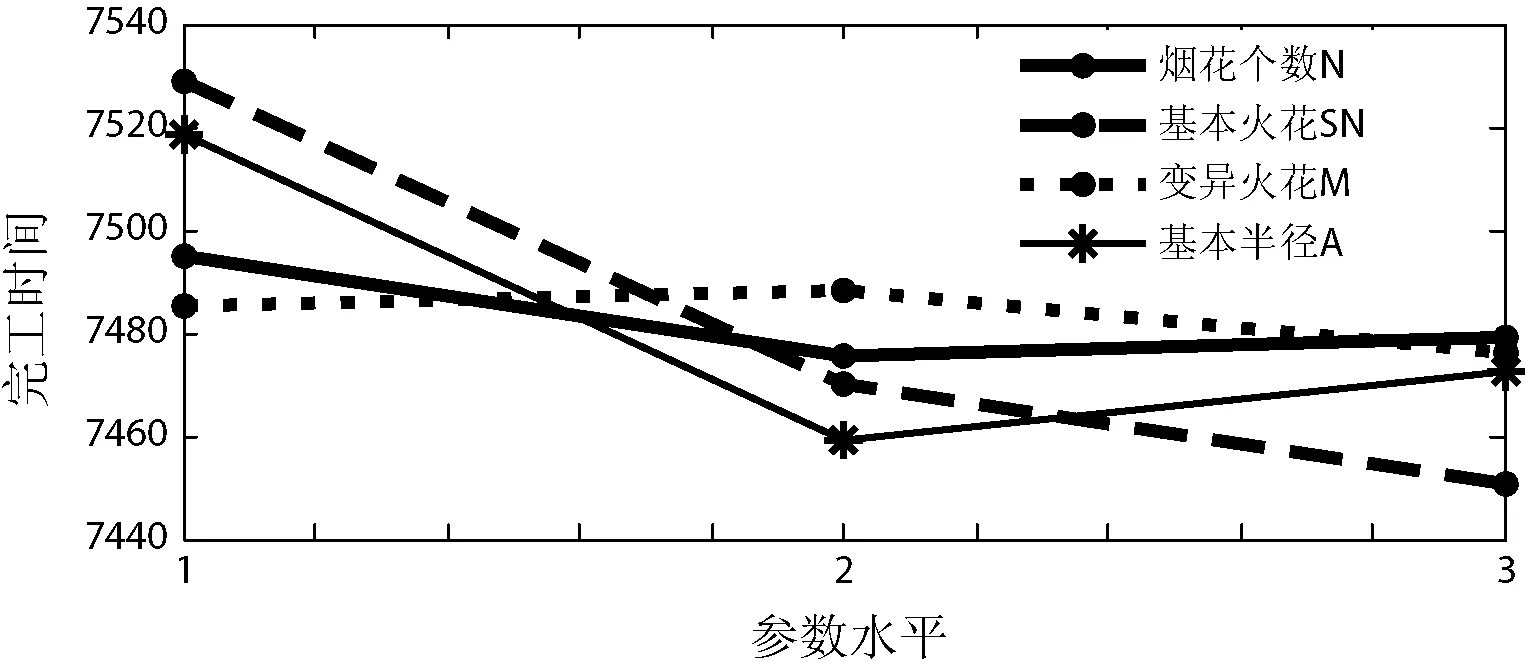
图1 不同参数水平下的寻优性能

通过以上分析，并结合实验数据，建议给出参数为：N=15,SN=40,M=15,A=5。

3.2 仿真实验

以Car类和Rec类基准问题为例[16]，同粒子群算法(PSO)、基本烟花算法(FWA)和萤火虫算法(FA)对比，测试改进烟花算法的寻优性能。

算法参数设置为：烟花算法中烟花个数N=15、基本火花个数SN=40、高斯火花个数M=15、基本半径5、最大边界5、最小边界-5；混沌烟花算法中，初始半径5、最终半径0.01、组规模0.3，其他参数与基本烟花算法一致；粒子群算法中粒子个数70、学习因子1.5、惯性权重0.9、最大边界5、最小边界-5、最大速度0.5、最小速度-0.5；萤火虫算法中种群规模70、光吸收系数1、最大吸引度1、步长因子0.2。以上每种算法均迭代300次，独立运行20次。仿真结果如表4和表5所示。

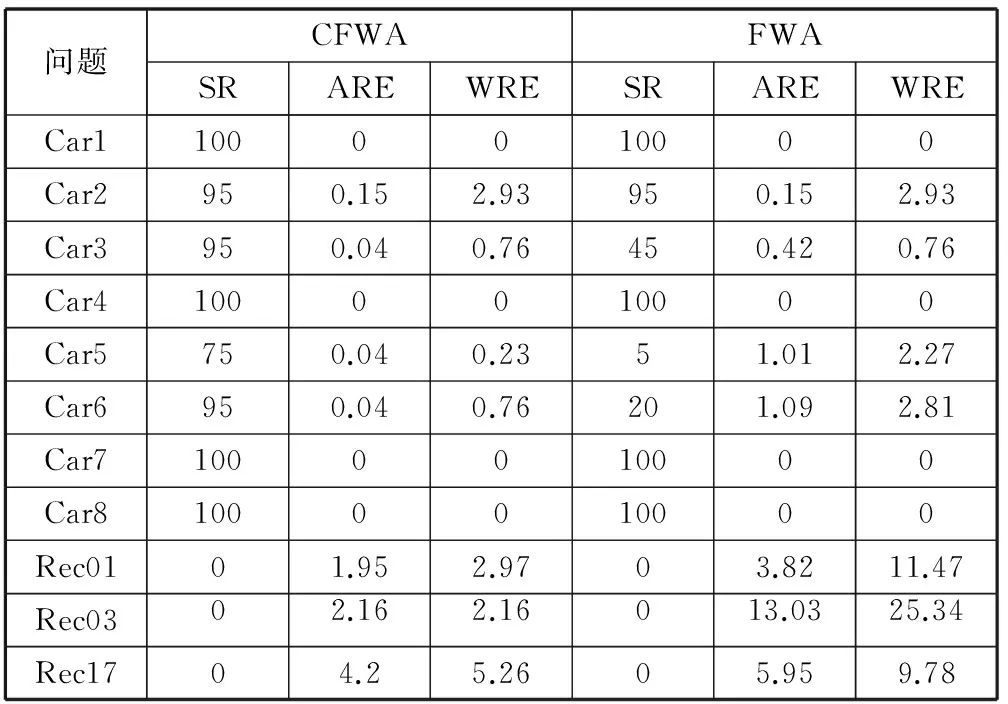
表4 算法寻优性能比较分析(CDWA和FWA)

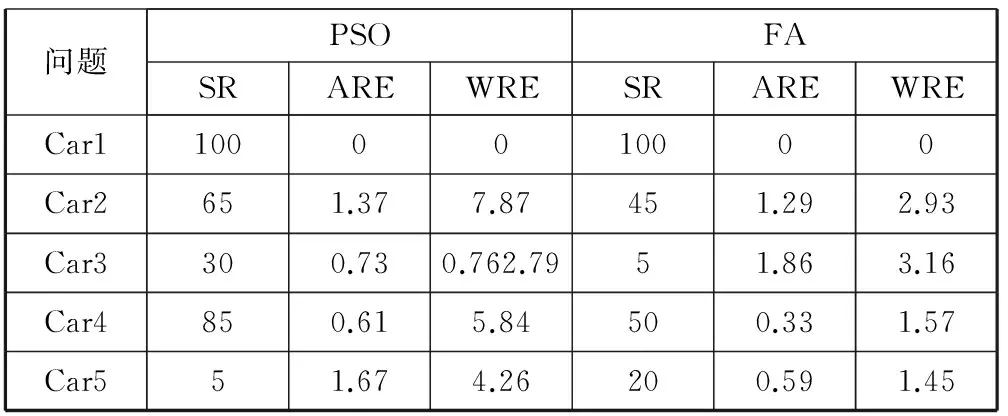
表5 算法寻优性能比较分析(PSO和FA)

续表5

针对Car类问题中较难寻优的Car3、Car5和Car6问题，绘制四种算法单次寻优曲线，如图2、图3和图4所示。

图2 Car3迭代曲线对比

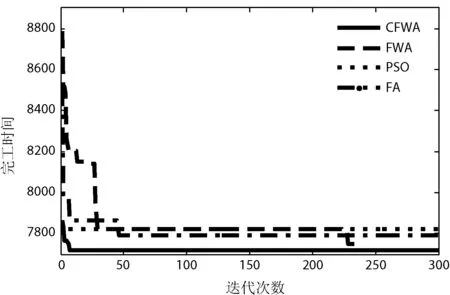
图3 Car5迭代曲线对比

图4 Car6迭代曲线对比

从寻优率上来看，较之于粒子群算法、萤火虫算法以及基本烟花算法，混沌烟花算法寻优率较高。混沌烟花算法在求解Car1、Car4、Car7和Car8问题时，寻优率达到了100%，求解其他Car类问题时寻优率也在一个较高水平。

从寻优稳定性上来看，混沌烟花算法在Car类所有问题，Rec01、Rec03和Rec17问题上平均偏移率ARE以及最大偏移率WRE均最小。与其他算法相比，混沌烟花算法每次寻优更能寻得最优或近似最优解。

从寻优速度来看，针对Car3、Car5和Car6问题，混沌烟花算法较之其他三种算法，收敛更快。从图2、图3和图4可以看出，混沌烟花算法可以在较短的迭代次数中，找到问题的最优解。对于Car3问题，烟花算法、粒子群算法和萤火虫算法均未找到其最优解，混沌烟花算法在第11代时找到最优解；对于Car5问题，混沌烟花算法和烟花算法分别在第9代和第230代找到问题的最优解，其他两种算法未找到最优解；对于Car6问题，只有PSO未找到问题最优解，混沌烟花算法、烟花算法和萤火虫算法分别在170代、220代和280代找到该问题的最优解。

4 结 语

在分析基本算法寻优机理的基础上，主要从编码、搜索半径、选择策略和精英混沌搜索四方面对原始算法加以改进。针对置换流水车间基准问题(Car类和Rec类)求解，混沌烟花算法在寻优率、寻优稳定性、寻优速度等方面较之烟花算法、粒子群算法和萤火虫算法具有一定的优势。对于烟花算法的改进策略是有效的，改进后的烟花算法可以用来求解置换流水车间问题。将来可以将改进算法应用于大规模置换流水车间调度以及其他离散调度(作业车间、可重入调度等)中去。

[1] Tan Y,Zhu Y C.Fireworks algorithm for optimization[C]//Advances in Swarm Intelligence.Springer,2010:355-364.

[2] He W R,Mi G Y,Tan Y.Parameter optimization of local-concentration model for spam detection by using local-concentration model for spam detection by using fireworks algorithm[C]//Advances in swarm intelligence.Springer,2013:439-450.

[3] Imran A M,Kowsalya M.A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using Fireworks Algorithm[J].International Journal of Electrical Power and Energy Systems,2014,62:312-322.

[4] Gao H Y,Diao M.Cultural firework algorithm and its application for digital filters design[J].International Journal of Modelling Identification and Control,2011,14(4):324-331.

[5] Zheng S Q,Tan Y.A unified distance measure scheme for orientation coding in identification[C]//Information Science and Technology (ICIST),2013 International Conference on.IEEE,2013:979-985.

[6] Zheng Y J,Song Q,Chen S Y.Multiobjective fireworks optimization for variable-rate fertilization in oil crop production[J].Applied Soft Computing,2013,13(11):4253-4263.

[7] 李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.

[8] 李新杰,胡铁松,郭旭宁,等.0-1测试方法的径流时间序列混沌特性应用[J].水科学进展,2012,23(6):861-868.

[9] 娄素华,吴耀武,熊信艮.电力系统无功优化的变尺度混沌优化算法[J].电网技术,2005,29(11):20-24,29.

[10] 张沫.改进混合蛙跳算法的云计算资源调度[J].计算机应用与软件,2015,32(4):330-333.

[11] Garey M R,Johnson D S,Sethi R.The complexity of flow shop and job shop scheduling[J].Mathematics of Operations Research,1976,1(2):117-129.

[12] 谭营,郑少秋.烟花算法研究进展[J].智能系统学报,2014,9(5):515-528.

[13] Qian B,Wang L,Huang D X,et al.An effective hybrid DE-based algorithm for multi-objective flow shop scheduling with limited buffers[J].Computers and Operations Research,2009,36(1):209-233.

[14] Awad El-Gohary,A S Al-Ruzaiza.Chaos and Adaptive Control in Two Prey,One Predator System With Nonlinear Feedback[J].Chaos,Solitons and Fractals,2007,34(2):443-453.

[15] 刘长平,叶春明.基于逻辑自映射的变尺度混沌粒子群优化算法[J].计算机应用研究,2011,28(8):2825-2827.

[16] 王凌.车间调度及其遗传算法[M].北京:清华大学出版社,2003.

APPLYING CHAOTIC FIREWORKS ALGORITHM IN SOLVING PERMUTATION FLOW SHOP PROBLEM

Cao Lei Ye Chunming Huang Xia

(SchoolofBusiness,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

We improved the fireworks algorithm to solve PFSP. By encoding with maximum position method, we mapped the continuous variables onto discrete space. To strike a balance between global searching and local searching, we introduced dynamic radius factor. We further mined the individual information with elite individual chaotic search. We replaced original selection operator with champion contest strategy, and as a result, the excellent ones in population could be selected at a higher rate of probability. We chose right parameters through orthogonal experiment for solving the benchmark problems of Car class and Rec class. Comparative experiments on basic fireworks algorithm, firefly algorithm and particle swarm optimisation illustrated that the improved chaotic fireworks algorithm has certain advantage over other algorithms in searching rate and searching speed and is an effective tool of solving permutation flow shop problem.

Fireworks algorithm Chaotic searching Permutation flow shop problem

2015-06-21。国家自然科学基金项目(71271138)；上海市一流学科建设项目(S1201YLXK)；沪江基金项目(A14006)；上海理工大学人文社科攀登计划项目(14XPB01)。曹磊，博士生，主研领域：智能算法，生产调度。叶春明，教授。黄霞，讲师。

TP301

A

10.3969/j.issn.1000-386x.2016.11.044