基于高斯混合PHD滤波的多目标状态提取方法

刘 益 王 平 高颖慧

(国防科学技术大学电子科学与工程学院 湖南 长沙 410073)



基于高斯混合PHD滤波的多目标状态提取方法

刘 益 王 平 高颖慧

(国防科学技术大学电子科学与工程学院 湖南 长沙 410073)

高斯混合概率假设密度滤波(GM-PHD)方法可有效解决线性高斯模型下的多目标跟踪问题，在估计目标个数的同时提取多目标状态。但当杂波浓度过高、目标过于密集时，GM-PHD的状态提取精度有所下降。针对GM-PHD滤波算法在复杂环境下性能下降的问题，提出一种改进的GM-PHD滤波多目标状态提取方法，通过修正高斯分量更新权值，强化合并规则，降低密集目标和杂波造成的干扰。仿真实验表明该方法能在不同杂波环境下提高多目标状态估计的准确度。

概率假设密度 高斯混合 多目标跟踪 状态提取

0 引 言

多目标跟踪旨在分析量测以获取个数时变的目标位置和速度等状态信息，量测包含真实目标量测和由于杂波、噪声引起的虚警量测。由于无法预先获知目标个数，传统的基于数据关联的多目标跟踪方法在跟踪多目标时适应性不强[1-4]。Mahler基于严格的随机有限集数学理论[5]，提出概率假设密度[6](PHD)滤波方法，通过递推多目标PHD，估计目标个数和位置，避免了数据关联问题。但PHD方法中存在高维积分，难以得到解析解。高斯混合概率假设密度滤波(GM-PHD)可对PHD滤波具体实现[7]。多目标PHD由一组高斯序列和，即所谓混合高斯近似表示。通过预测、更新步骤递推高斯混合函数中每一高斯分量的权值、均值和协方差，间接递推多目标的后验PHD。根据高斯分量信息估计多目标状态，当目标过于密集，噪声、杂波等干扰较严重时，估计精度会降低。为解决此问题，提出一种改进的基于高斯混合概率假设密度滤波的多目标状态提取方法，以满足较为复杂场景下的多目标状态提取要求。

1 高斯混合概率假设密度滤波

1.1 随机有限集与PHD滤波

随机集即为一个随机变量的集合，是指取值为集合的随机元，是概率论中随机向量的推广。当随机集的取值是有限值时就成为随机有限集(RFS)。多目标跟踪系统中，目标个数是一随时间变化的离散随机变量，因而将多目标集表示为随机有限集时，集合中随机变量的个数本身就是一个随机变量，导致多目标的状态空间和量测空间的维数也会随着时间变化。多目标的状态空间和量测空间分别以Es、Eo表示，则k时刻多目标状态集Xk和量测集Zk为：

Xk={xk,1,…,xk,Mk}⊆Es

Zk={zk,1,…,zk,Nk}⊆Eo

(1)

其中Mk、Nk分别表示k时刻的目标个数和量测个数，其中量测来自于真实目标和虚警。

以随机有限集Ξk和Σk分别对多目标的状态和量测建模。假设Xk-1是RFSΞk-1在k-1时刻的具体实现，则k时刻多目标的状态以随机集表示为：

Ξk=Sk(Xk-1)∪Bk(Xk-1)∪Γk

(2)

其中，Sk(Xk-1)表示k时刻继续存活目标的RFS，Bk(Xk-1)代表由k-1时刻的目标状态Xk-1衍生出的目标的RFS，Γk代表在k时刻自然产生的目标的RFS。多目标的量测以随机有限集可表示为：

Σk=Ek(Xk)∪Ck(Xk)

(3)

其中Ek(Xk)表示产生于Xk的观测值的RFS，Ck(Xk)代表杂波或误警生成的RFS。

根据多目标Bayes滤波理论，可得：

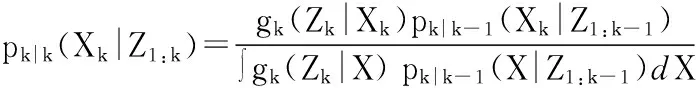
(4)

其中，pk|k-1(Xk|Z1:k-1)和pk|k(Xk|Z1:k)分别表示多目标联合先验概率密度函数和后验概率密度函数。

随机有限集的PHD D(x)与随机变量的期望类似，即PHD D(xk|Z1:k)即为多目标后验概率密度pk|k(Xk|Z1:k)的一阶矩。在多目标跟踪系统中，∫sD(x)dx是出现在S内的期望的目标数，而D(x)的极值给出目标的状态估计。以PHD代替后验概率密度以贝叶斯滤波方式递推，便得到PHD的预测和更新方程如式(5)、式(6)所示[6]:

Dk|k-1(x)=∫pS,k(ζ)fk|k-1(x|ζ)Dk-1(ζ)dζ+∫βk|k-1(x|ζ)Dk-1(ζ)dζ+γk(x)=∫φk|k-1(x,ζ)Dk-1(ζ)μsdζ+γk(x)

(5)

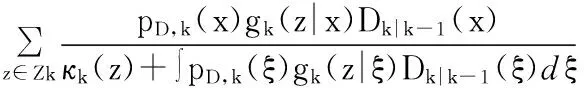
(6)

其中γk(x)表示随机集Γk的PHD，βk|k-1(x|ζ)表示由k-1时刻状态为ζ的目标衍生的随机集βk|k-1(ζ)的PHD；pS,k(ζ)表示k-1时刻状态为ζ的目标在k时刻仍然存活的概率；fk|k-1(x|ζ)表示单个目标的转移概率密度,κk(z)=λkck(z)，λk表示Poisson杂波的平均数，ck表示杂波概率密度；pD表示检测概率，gk(z|ξ)表示单个目标的似然函数。

PHD滤波仍然包含多重高维积分，得不到闭合形式的解析解。高斯混合PHD滤波是PHD滤波的一种简单近似，解决了难以具体实现的问题。

1.2 GM-PHD滤波

(7)

其中Jk-1表示k-1时刻高斯分量的个数。N代表正态分布。假设目标的运动观测均为线性模型。其转移概率密度与观测似然函数为

fk|k-1(x|ξ)=N(x;Fk-1ξ,Qk-1)gk(z|x)=N(z;Hkx,Rk)

(8)

其中Fk-1、Hk分别为线性状态转移矩阵和线性观测矩阵，Qk-1、Rk为过程噪声和量测噪声协方差。

将高斯混合形式的PHDDk(x)代入PHD预测、更新方程，可得到高斯混合形式的PHD递推形式。k时刻的预测、更新PHD以高斯混合可分别表示为：

(9)

(10)

其中：

(11)

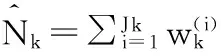
2 改进的高斯混合PHD滤波

2.1 权值修正

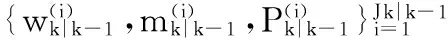
(12)

代入式(11)，则第m个高斯分量由第n个量测zn更新后的权值为:

(13)

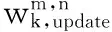
(14)

对于量测zn会出现以下两种情形:

(15)

第一种情形对应第n个量测zn由某一真实目标生成的情况。当观测空间没有虚警杂波量测时等号成立。第二种情形对应第n个量测zn为虚警杂波的情况，根据其与各个高斯分量均值的似然关系，其对应更新权值极小，表明该量测与当前预测高斯分量相关性极低。

以上两种情形体现在更新矩阵W中即为第n列的权值和不大于1。其现实意义是一个量测至多只由一个目标生成(考虑虚警情形)。每时刻完成高斯分量权值更新后，每一列的权值和必定满足上述性质，这是由GM-PHD滤波的递推特性决定的。

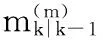
(16)

体现在更新矩阵W中即为第m行的权值和大于1，表示第m个高斯分量(隐指一个目标)生成了多个量测。在现实中，考虑漏检的影响，一个目标至多生成一个量测。因此这种更新方式会错误地把多个量测分配给一个目标并以较高权值进行更新，导致状态估计结果错误或冗余。

为此对矩阵W的行权值修正，使其行权值和不大于1，即满足一个目标至多生成一个量测的实际条件。

(17)

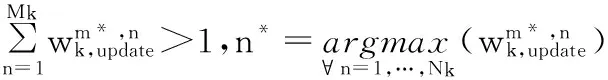
行权值修正操作会改变原有列权值的“归一化”秩序。对于第一种情形，即第n个量测zn由某一真实目标生成的情况,W矩阵中第m*行n列的权值由于行权值修正操作而减小。为使第n列的权值和满足式(14)的条件，也即使该列符合真实量测必定源于某一目标的实际条件，需要对第n(n≠n*)列进行列权值修正：

(18)

第n(n≠n*)列列权值修正过程保留因第m*行行权值修正而减小的(m*,n)处的权值，使得该列其他权值按各自比重相应增加，提高第n个量测相对其他高斯分量(不包含第m*个分量)的似然度。因为由行权值修正过程已得知，仅第n*个量测最有可能源于第m*个高斯分量或目标。

对于第二种情形，由于量测zn本身为杂波虚警，由其更新的各个高斯分量的权值极小，可视为零。故对第m*行行权值修正时不会改变(m*,n)处零权值的性质，对应第n列的权值和仍然满足式(14)，不需要进行列权值修正。故在进行列权值修正前，应先大致判别该量测是否为虚警杂波，再决定是否修正列权值。当权值更新矩阵W中第n列的权值和高于某一阈值wth时可施行列权值修正操作。文献[8,9]中对所有的量测均进行重归一化处理会会导致资源的浪费，增加运算时间。权值修正方法流程如图1所示。

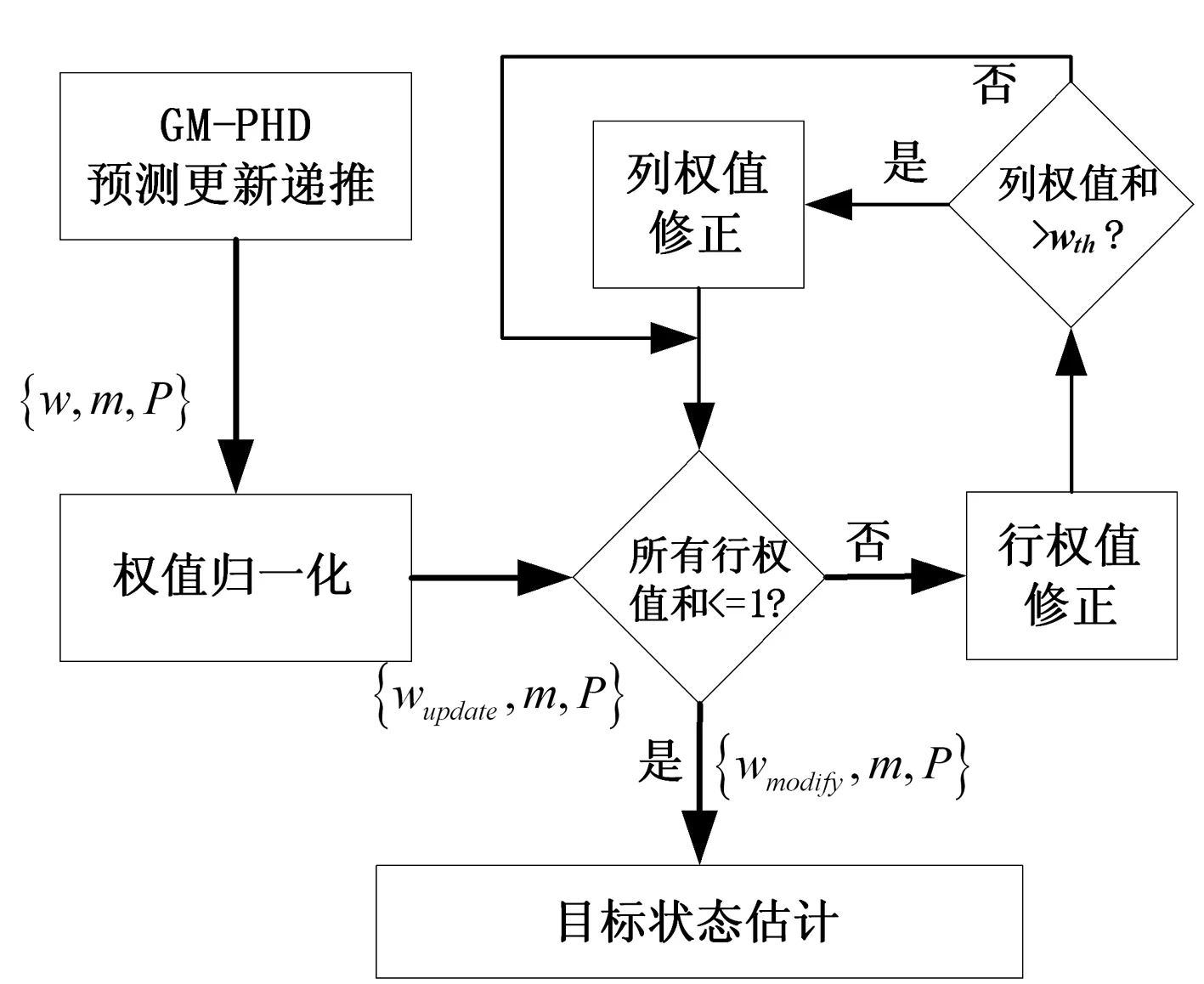
图1 权值修正流程图

进行行权值与列权值修正的目的在于使更新权值满足以下条件：一个量测至多源自一个目标，一个目标生成至多一个量测。从而提高状态估计的精度。

2.2 高斯分量选择性合并

每时刻更新后的高斯分量个数会爆炸式增长，因此Vo提出在高斯分量权值更新后引入剪枝操作[7]，将低于阈值T的高斯分量删除，仅保留高权值高斯分量，用以控制高斯分量个数，减小运算量。

对于剪枝后的高斯分量采取合并的方式，将多个相互靠近即满足如下条件的高斯分量合而为一[10]：

(19)

但当目标较为密集时，按照原有的合并规则会导致代表相近不同目标的多个高斯分量合并，即原本代表多个不同目标的高斯分量被合并后的一个高斯分量所代替，则由合并后的高斯分量估计出的目标状态会丢失部分真实信息。

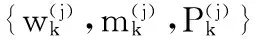
(20)

选择性合并后的高斯分量的均值、权值和协方差矩阵的计算与文献[7]一致。对合并后的高斯分量集合进行状态提取，将权值较高的高斯分量的均值视为估计状态，至此完成该时刻的状态估计。将合并后的混合高斯PHD传入下一时刻。

假设新生目标和衍生目标的概率密度均可用如下高斯混合的形式表示:

(21)

(22)

k-1时刻的PHD如式(7)所示,与式(21)、式(22)一并代入式(5)，得到如式(9)所示的预测后高斯混合形式。对于更新步骤，在原有更新权值的基础上[7]采用本文提出的权值修正策略，对权值调整，使其符合现实情况。针对更新后的高斯分量，加强合并条件，防止错误合并，权值高于设定阈值(通常取0.5)的高斯分量的均值即为k时刻多目标的状态估计。

3 仿真结果及分析

设定目标在某一二维杂波区域[-1000,1000] m×[-1000,1000] m内运动，目标的运动服从高斯线性模型为:

(23)

(24)

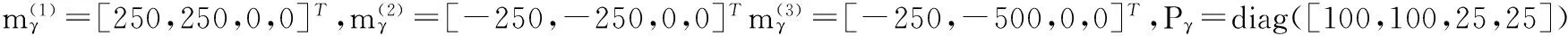
系统的观测模型为:

(25)

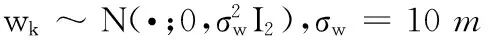
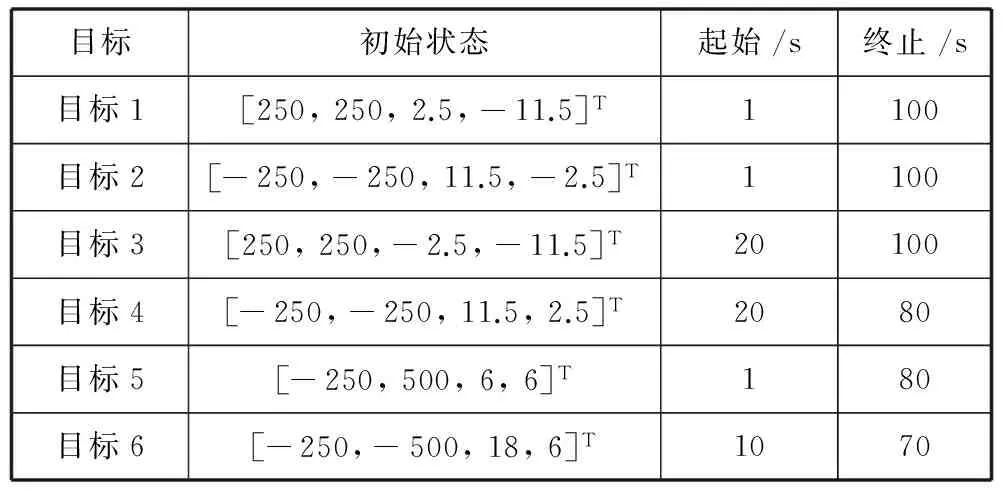
表1 目标初始状态与生存时间

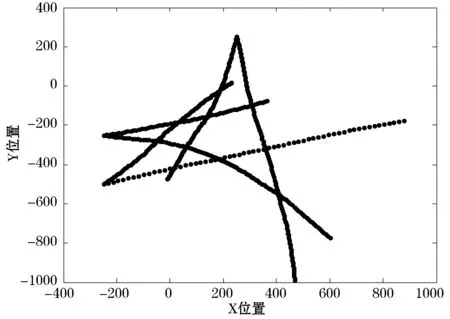
图2 目标真实状态

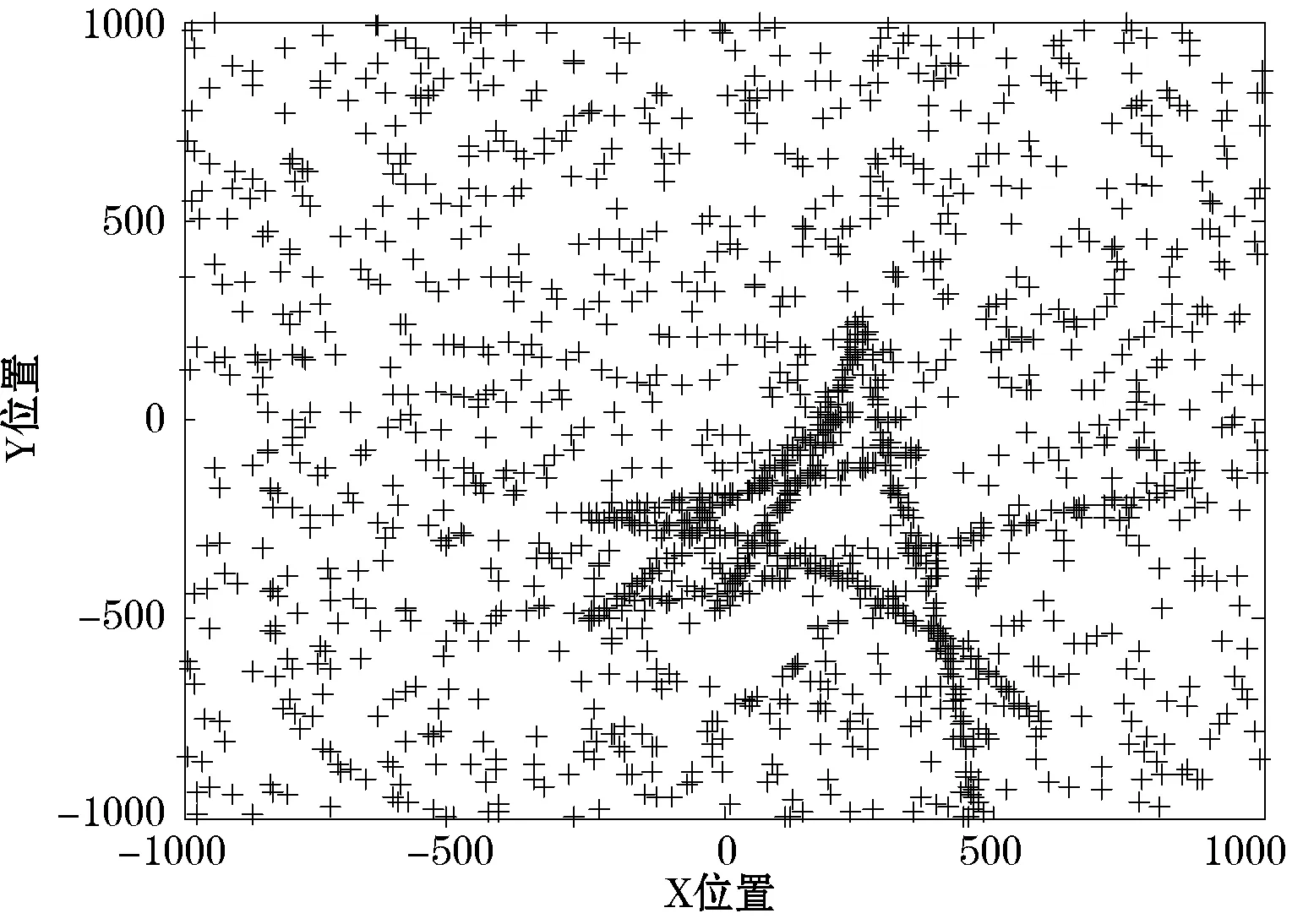
图3 量测

图4和图5分别给出了GM-PHD滤波算法和本文提出的改进算法的多目标状态提取结果，实线代表目标的真实轨迹，“·”代表估计出的目标位置。从图中可以看出，改进算法的状态提取结果相对于原有算法的结果更为准确，估计出的目标位置要更加集中，与目标的真实轨迹贴合更加紧密。

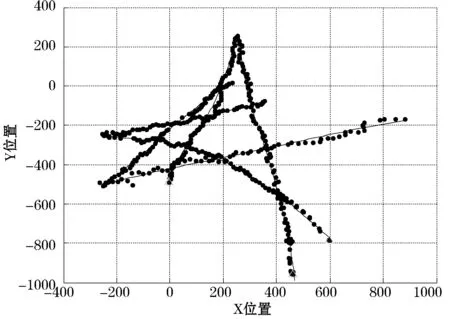
图4 GM-PHD状态估计

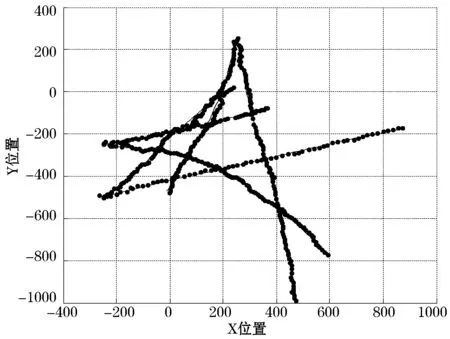
图5 改进算法状态估计

为进一步分析状态提取的精度，采用OSPA准则[11]评估算法性能。OSPA评价指标引入了截断常数c，能够处理两个随机集之间目标个数不一致时的性能评价。在本文中截断常数c为100。图6给出了两种算法在20次MC仿真条件下的OSPA均值距离。距离越小表示估计结果越精确。由图可知，改进算法的OSPA曲线大体低于GM-PHD滤波状态提取算法，表明本文改进算法具有良好的估计精度。

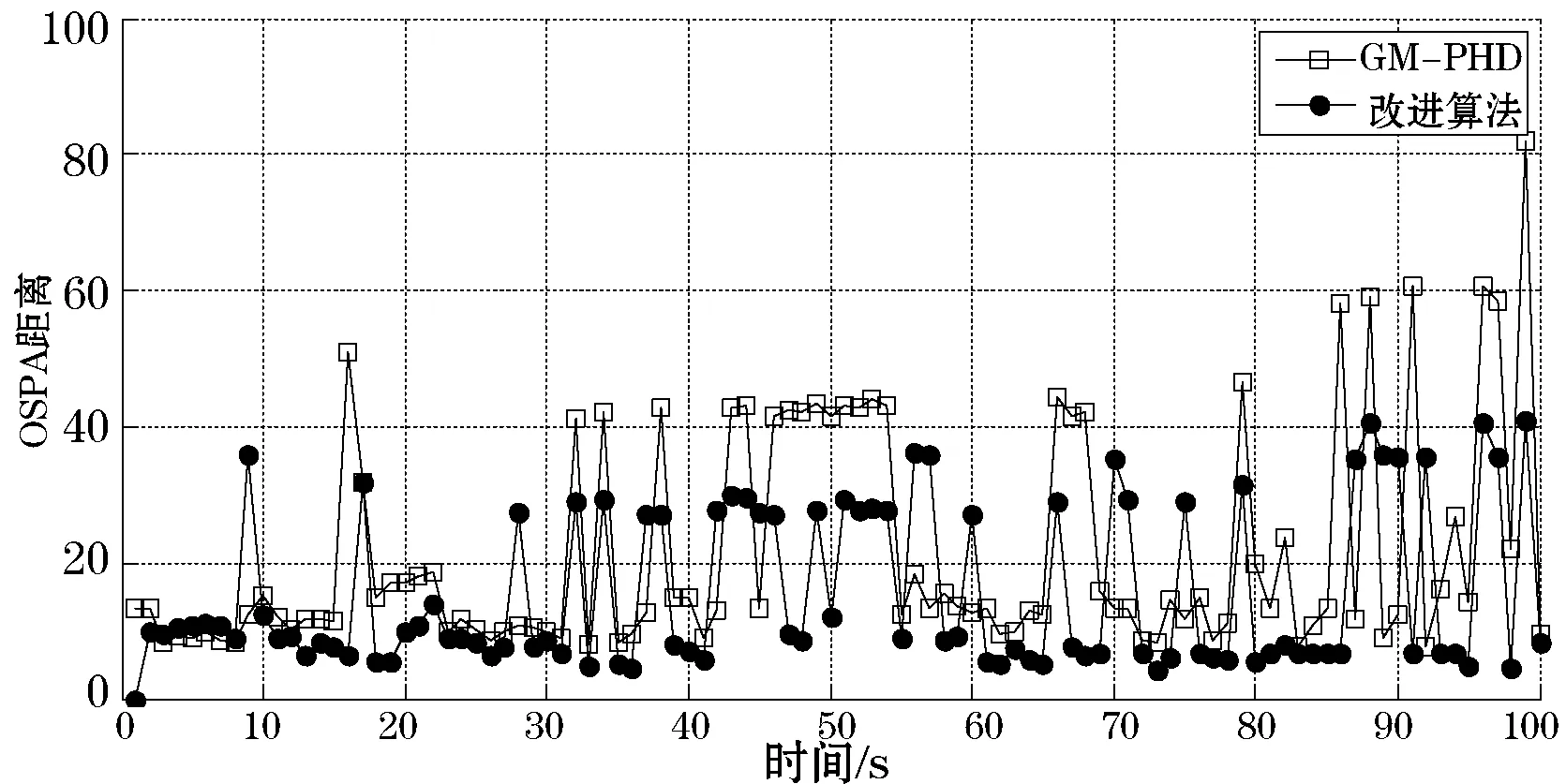
图6 OSPA距离

当每时刻的杂波虚警个数的均值为100时，由真实目标生成的量测会被大量不相干噪声点湮没。即在不进行权值修正的情况下，会经常出现一个目标与多个量测相对应的情况，导致多目标状态估计的错误，为说明此问题，图7给出了两种算法在高浓度虚警条件下的平均OSPA距离。相比于低杂波浓度的情形(图6)，两种算法的OSPA距离均有明显增大，这是由大量虚警量测导致的必然结果。但总体而言，改进算法的OSPA距离依然要低于GM-PHD滤波状态提取算法，说明了在目标、虚警密集等严苛条件下，改进算法的性能有所提升。

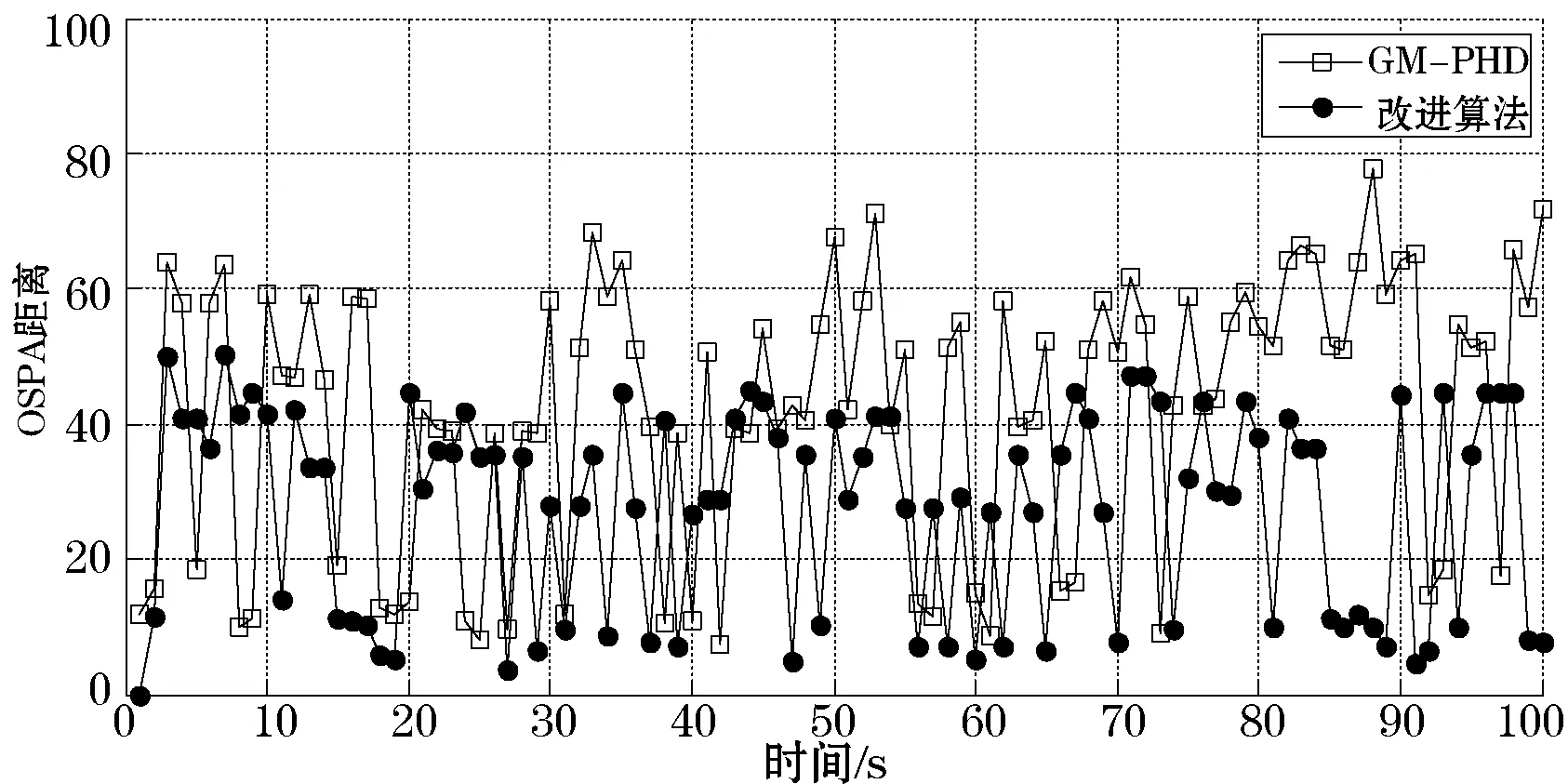
图7 OSPA距离

4 结 语

本文在原有GM-PHD滤波方法的基础上，修正更新高斯分量的权值，并加强高斯分量合并规则，以减轻目标密集和虚警杂波对算法造成的影响。下一步可针对非线性非高斯模型进一步改进高斯混合PHD滤波状态提取算法，扩展其应用范围。

[1] Samuel Blackman, Robert Popoli. Design and analysis of modern tracking systems[M].London: Artech House, 1999:7-12.

[2] Poore A B. Multidimensional assignment formulation of data association problems arising from multitarget and multisensor tracking [J]. Computational Optimization and Applications,1994,2(3): 27-57.

[3] Barshalom, Rong Li, T Kirubarajan. Estimation with applications to tracking and navigation[M].USA: John Wiley & Sons, Inc, 2001:33-39.

[4] 林两魁.天基红外传感器对中段弹道目标群的跟踪与超分辨技术研究 [D].长沙：国防科学技术大学，2013.

[5] Mahler R. Multitarget bayes filtering via first order multi-target moments [J]. IEEE Trans. on Aerospace and Electronic Systems, 2003, 39(4):1152-1178.

[6] Mahler R. Statistical multisource-multitarget information fusion[M].Boston :Artech House, 2007: 711-715.

[7] Vo B N，Ma W K.The gaussian mixture probability hypothesis density filter [J].IEEE Transactions on Signal Processing，2006，54(11)：4091-4104.

[8] Mahdi Yazdian. An improvement on GM-PHD filter for occluded target tracking[C].ICASSP,2013：1773-1776.

[9] Hongwei Ge. Improved gaussian mixture PHD for close multi-target tracking[C].Information Technology and Artificial Intelligence Conference , 2014：311-315.

[10] Fuliang Yin, Liming Chen, Zhe Chen.A novel merging algorithm in gaussian mixture probability hypothesis density filter for close proximity targets tracking [J] . Journal of Information and Computational Science, 2013, 8(12) 2283-2299.

[11] Schuhmacher D, Vo B T, Vo B,N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Trans. Signal Process, 2008,56(8): 3447-3458.

MULTI-TARGET STATE EXTRACTION BASED ON GAUSSIAN MIXTURE PHD FILTER

Liu Yi Wang Ping Gao Yinghui

(CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,Hunan,China)

Gaussian mixture probability hypothesis density (GM-PHD) filter can effectively solve the problem of multi-target tracking under the condition of linear Gaussian model, while estimating the number of targets it also extracts the states of multi-target. The state extraction precision of GM-PHD filter will drop down when it comes to the situation of closely spaced targets and too high clutter rate. In light of the performance degradation of GM-PHD in complex environments, we proposed an improved multi-target state extraction method of GM-PHD filter. By modifying the update weight of Gaussian component and enhancing the merging criterion it reduces the interference caused by intensive targets and clutters. Simulation experimental results showed that the propose method is able to raise the precision of multi-target state estimation in different clutter environments.

Probability hypothesis density Gaussian mixture Multi-target tracking State extraction

2015-09-19。国家自然科学基金项目(61103082)。刘益，硕士生，主研领域：目标跟踪与自动目标识别。王平，研究员，高颖慧，副研究员。

TP391.4

A

10.3969/j.issn.1000-386x.2016.11.041