鲁棒的各向异性扩散三维超声图像去噪算法

骆科扬 刘 俊

(武汉科技大学计算机科学与技术学院 湖北 武汉 430081)



鲁棒的各向异性扩散三维超声图像去噪算法

骆科扬 刘 俊

(武汉科技大学计算机科学与技术学院 湖北 武汉 430081)

针对三维超声图像去噪，提出一种新的各向异性扩散滤波算法。该算法主要通过改进传统算法中的扩散系数以及瞬时变化系数(ICOV)，在保留三维超声图像边缘和细节的同时，更好地滤除了斑点噪声。与传统算法相比，该算法对迭代次数有更低的敏感度和更好的鲁棒性。

三维超声图像 各向异性扩散 斑点去噪 鲁棒性

0 引 言

超声成像技术被广泛地运用于妊娠诊断[1]、肿瘤检测[2]和性别鉴定[3]等领域，与核磁共振成像和CT等其他成像技术相比，具有价格低廉、实时性、非放射性和非入侵性等显著特点。目前广泛使用的是二维超声成像技术，但是二维超声存在着不可克服缺点[4,5]。例如二维超声图像对器官的一些任意角度所呈现的平面非常薄，因此很难对图像平面进行定位；二维超声技术亦无法显示病灶及器官的内部信息。而三维超声成像技术可以克服这些缺点，因此，近年来三维超声成像技术逐渐发展起来，并在某些领域取代了二维超声成像技术。比如陈慧贞等[6]基于三维超声成像技术为斑块定量分析提供了一种新的方法，相比于传统的二维超声成像，新方法能更好地显示斑块立体形态并能够更加准确测量斑块大小。但是三维超声成像由于数据采集困难，图像对比度低、斑点噪声严重，组织器官特征不易分类等不利因素的限制，成像质量不高。因此为了便于对三维超声图像进行分割等后续操作，需要在不破坏超声图像重要特征的前提下尽可能地滤除斑点。

对受到大量乘性噪声(亦称斑点)污染的超声图像，Yu等[7]提出了斑点降噪各向异性扩散(SRAD)算法。该方法能较好地识别超声图像中的灰度变化是由斑点噪声还是边缘引起的，能避免与边缘方向垂直的平滑，加强与边缘水平方向的平滑。Aja-Fernandez等[8]提出了一种边界保留性能比较好的去噪方法DPAD。Tauber等[10]通过使用与SRAD算法相同的ICOV，结合Black等对各向异性扩散滤波的鲁棒性理论[9]，提出了一种更加稳定的去噪算法；Liu等[11]提出了一种边界保留和鲁棒性都较好的去噪方法RDPAD；王常虹等[12]提出了一种基于中值滤波的各向异性扩散的超声图像去噪算法；李灿飞等[13]通过改进扩散系数, 提出一种新的斑点噪声各项异性扩散模型；陈婷婷等[14]提出了一种复合各向异性扩散的图像去噪算法。这些算法都是在SRAD的基础上，改进了SRAD的去噪能力和算法的鲁棒性，但是这些算法都局限于二维超声图像的斑点去噪。

随着三维超声成像技术的发展，Sun等[15]对SRAD进行改进，将其拓展并应用到三维超声图像中，提出了一种真正意义上的三维超声图像去噪方法3DSRAD。类似地，Tang等[16]基于各向异性扩散滤波算法，开发了一种适用于三维超声图像去噪的滤波算法。通过Aja-Fernandez等人在二维超声图像上对SRAD的改进取得的成功可以推测，在三维超声图像中，3DSRAD的去噪能力及算法的鲁棒性，亦有较大的提升空间。

1 背 景

1.1 二维图像中的各向异性扩散滤波算法

文献[7]在分析讨论了各向异性扩散模型和Lee滤波器的联系之后，提出了适用于斑点去噪的SRAD模型[7]，该模型总体上可以表示为：

(1)

式中：I为二维图像，▽为梯度算子，div为散度算子，c(x)为扩散系数。扩散系数的具体定义如下：

(2)

q(x,y;t) 为二维下的瞬时变化系数(ICOV)，表达式为：

(3)

针对二维超声图像斑点去噪的另一著名算法是Aja-Fernandez结合各项异性扩散滤波和Kuan滤波器提出的边界保留性能较好的去噪模型DPAD[8]，在DPAD模型中，扩散系数为：

(4)

相应地，q(x,y;t)采用了新的计算方法，具体定义如下：

(5)

DPAD模型和SRAD模型都有较强的斑点去噪能力，但是DPAD模型对迭代次数的敏感性要低于SRAD模型。

1.2 三维图像中的各向异性扩散滤波算法

在三维超声图像去噪方法中，如果简单地采取类似二维超声去噪算法的处理方式，将三维图像看成一组二维的图像切片的集合，对每一个切片进行二维去噪处理(B-SCAN方法)。由于充分运用切片层之间的像素信息，往往得不到理想的斑点滤除效果。因此，文献[15]通过对三维图像下的各向异性扩散滤波算法的分析，基于SRAD模型提出了一种真正意义上的三维超声图像去噪方法3DSRAD，此模型总体上可以表示为：

(6)

式中：I为三维图像，▽为梯度算子，div为散度算子，c(x)为扩散系数，均作用于三维空间。其中扩散系数相对来说比较复杂，具体表达式如下：

(7)

式中：

(8)

(9)

随后文献[16]通过改进扩散系数，提出了新的去噪方法，其在新方法中使用的扩散系数为：

(10)

以上两种三维超声斑点去噪模型均利用了切片间的联系信息，取得了不错的斑点滤除效果，同时对图像的边缘也有较好的保护。但3DSRAD只是SRAD模型在三维空间中一种推广，从文献[11-14]等对SRAD的改进工作可以看出，3DSRAD模型的去噪能力和鲁棒性亦尚有较大的提升空间。

2 本文算法

2.1 扩散系数和ICOV的改进

各向异性扩散滤波模型，即PM模型[17]提出了两种形式的扩散系数：

(11)

(12)

在式(11)、式(12)中，k为梯度阈值，通常根据实际图像估计为常数。本文的方法所用的扩散系数则结合了这两种系数的优点。

首先将DPAD模型中的扩散系数拓展到三维空间中，由式(4)可推得：

即得到了类式(12)的扩散参数，令:

(13)

将φ(x,y,z;t) 整体代入式(11)，可得：

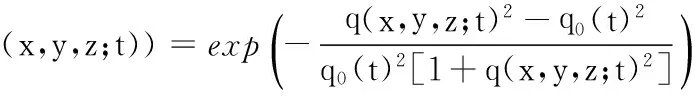
(14)

鉴于文献[11，14]在对SRAD改进时将阈值引入扩散系数取得的成功，本方法亦对ICOV进行相应的阈值判断处理，从而得到了三维下全新的瞬时变化系数：

c(q)=

(15)

即：

c(q)=

(16)

可以看出，当φ(x,y,z;t)大于阈值σe时，将扩散系数置0，亦即对于图像中梯度级大于σe的邻域将对当前像素值不会有影响。因此，基于这样的扩散系数的滤波算法即使经过多次的迭代仍旧可以得到清晰的边缘。在本模型中σe的取值应根据实际的图像进行选取，在后续的实验中，本模型取σe为1。

对于q(x,y,z;t)的计算。对于瞬时变化系数(ICOV)，即q(x,y,z;t)的计算,根据式(5)拓展到三维空间中，则有：

(17)

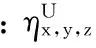
2.2 算法的实现

本文提出的鲁棒的各向异性扩散三维超声图像去噪算法的算法流程如图1所示。

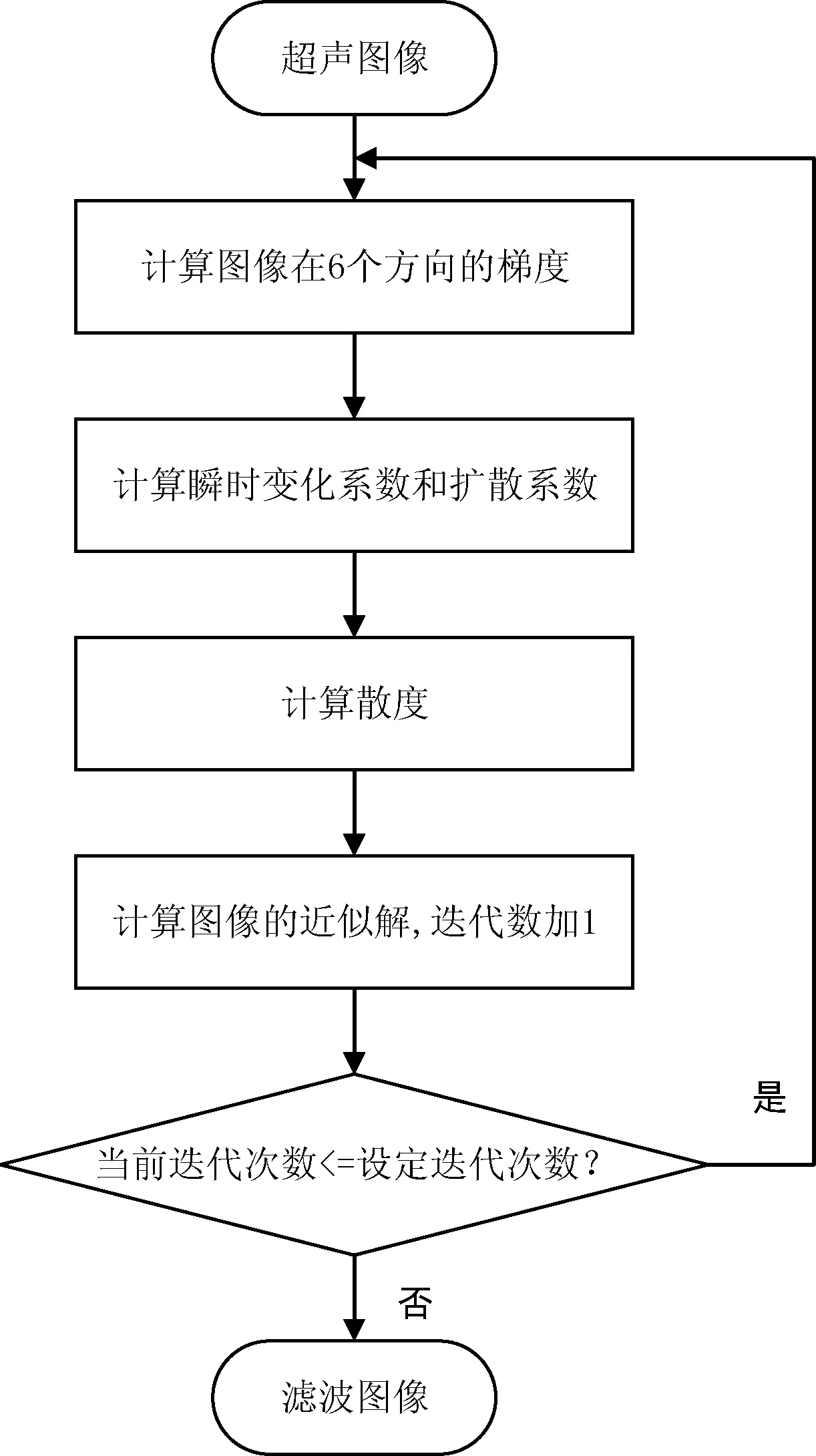
图1 本文算法流程图

总体上分为4步，各步涉及的数学模型解释如下：

(1) 计算图像在6个方向的梯度

(18)

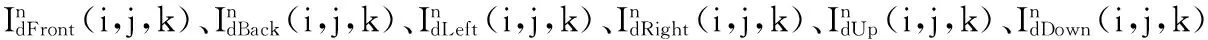
(2) 计算瞬时变化系数和扩散系数

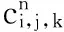
(3) 计算c(·)▽I的散度

(19)

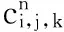
(4) 计算图像的近似解

(20)

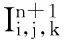
3 实验结果及对比

本文中的所有实验均使用主频为2.0 GHz、内存为6 GB的PC机上完成，使用MATLAB 2014b作为编程工具。

3.1 图 像

实验采用的三维超声图像是由麦迪逊超声机采集的真实牛卵泡图像，图像含大量斑点噪声，其x、y和z方向大小分别为800×600×41(单位: 像素)，像素点为256灰度级。为了保证计算的精度，在实验中将其转换为DOUBLE型。实际操作过程中，我们对X-Y平面上感兴趣的卵泡区域进行了截取预处理，处理后的三维牛卵泡超声图像x、y和z方向大小分别为128×128×41(单位: 像素)，该区域既完整地包含了卵泡，又尽可能地减少了其他冗余图像信息，从而提高了处理效率。

3.2 评价方法

(1) 斑点噪声抑制程度

对于斑点噪声抑制程度的比较，根据文献[15]在3DSRAD中使用的方法，采用图像同质区的对比度值进行量化比较，其具体计算公式如下：

(21)

式中：Ω为超声图像I中的某一同质区域，N为该区域像素点的个数，C(x,y,z)的定义如下：

(22)

其中Imax(x,y,z)和Imin(x,y,z)为点(x,y,z)以及它2n+1邻域像素值的最大值和最小值。对斑点去噪算法，在图像的同质区，去噪处理后的C值应该远比处理前的值要小，即可认为C值越小，算法的斑点滤除能力更强。

(2) 算法鲁棒性

为了比较传统3DSRAD算法和本文算法对迭代次数的敏感程度，我们采用的方法如下：对同一三维超声原始图像进行多次迭代，在两种方法得到的结果中选取一个XY剖面，然后对该剖面某高度位置的灰度值进行多次观测，利用灰度值的变化来比较算法的鲁棒性。

3.3 实验对比

(1) 斑点噪声抑制程度对比

在计算C值时，我们使用的是同一三维超声图像分别经3DSRAD模型和本文新模型迭代100次后在相同位置处获得的10张XY平面的连续切片，表1为实验中获得的结果。显然，这两种算法处理后的C值都比处理前小很多，且经本文方法处理后的平均C值比3DSRAD减少了0.00358，表明本文方法的斑点滤除能力优于3DSRAD。

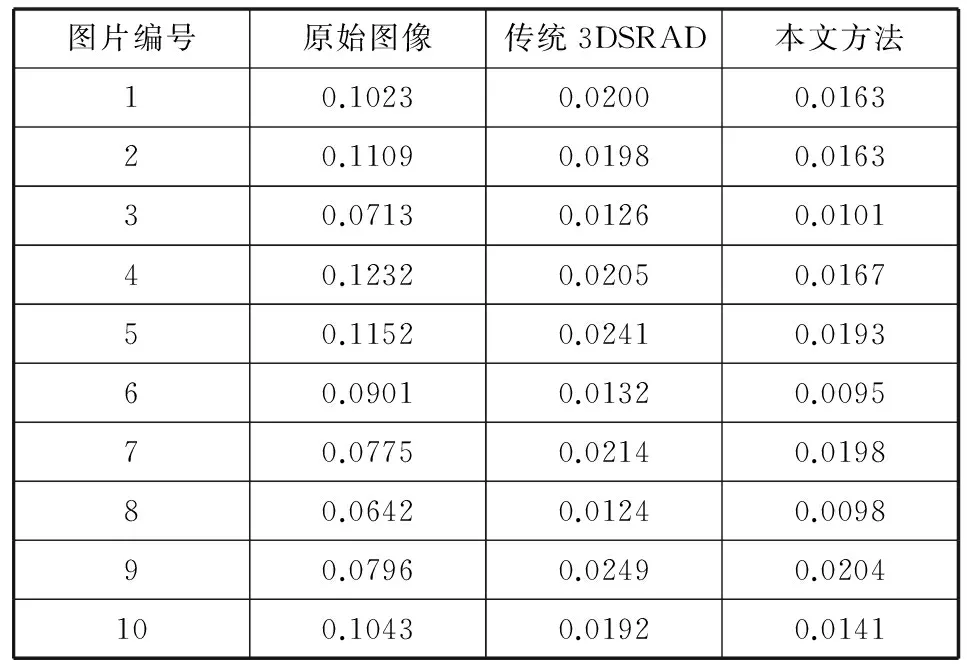
表1 去噪后图像同质区的对比度值

(2) 算法鲁棒性比较

对同一三维牛卵泡超声图像分别使用传统的3DSRAD和我们改进的算法进行去噪，迭代次数(记为iter)分别为50、100、200和500次。处理结束后取三维图像中心位置处XY平面切片，得到的结果如图2、图3所示。

图2 3DSRAD去噪后XY平面切片

图3 本文方法去噪后XY平面切片

从图2与图3直观上比较可以看出本文方法对迭代次数的敏感度比3DSRAD算法要低。

为了进行定量地精确比较，在算法迭代过程中对图2与图3中高度为64处扫描线进行相应的数据统计，得到结果如图4、图5所示。

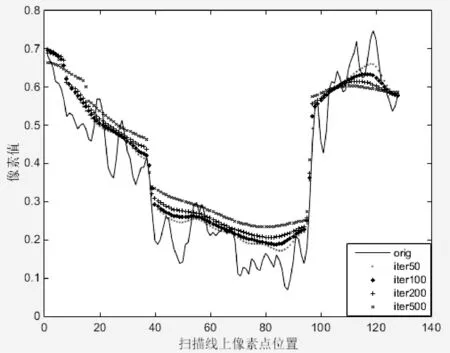
图4 3DSRAD算法迭代敏感度曲线

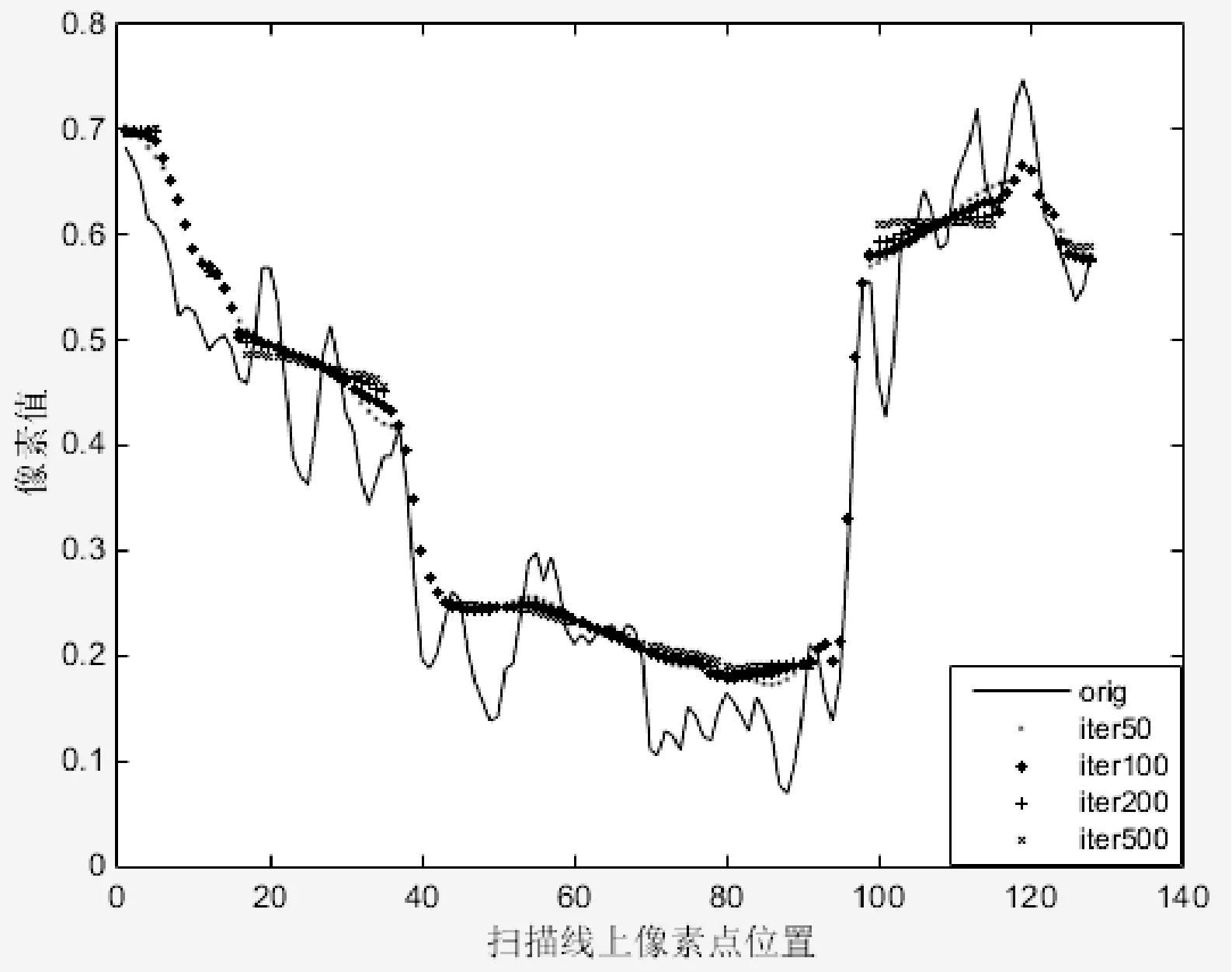
图5 本文算法算法迭代敏感度曲线

从图4与图5定量对比分析可以看出：与传统的3DSRAD算法的结果相比，改进后的算法对迭代次数不敏感。通过以上定性比较和定量分析，说明了改进后的滤波算法的鲁棒性优于传统的3DSRAD算法。

4 结 语

本文通过结合PM模型中两种扩散系数，对三维超声图像下各向异性扩散滤波算法的扩散系数进行改进，提出了一种新的各向异性扩散滤波模型。相较于传统的3DSRAD算法，本文新模型能够在较好保留图像边缘的同时，更好地滤除斑点噪声。此外，新模型对处理过程中的迭代次数有更低的敏感度，大大提高了算法的鲁棒性。实验结果表明，改进后的算法要比3DSRAD算法更优，该方法作为牛卵泡三维超声图像预处理的第一步，可以更好地增强后续的牛卵泡分割效果。

[1] 王银,李谊,钱隽,等.早期宫角妊娠的超声诊断与鉴别诊断[J].中国超声医学杂志,2014,30(12):1117-1119.

[2] 徐静,高鑫.超声乳腺肿瘤的全自动SVM检测与水平集分割算法[J].计算机辅助设计与图形学学报,2012,24(5):662-668.

[3] 艳芳,叶明伟.早期宫角妊娠的超声诊断与鉴别诊断[J].医学影像学杂志,2012,22(10):1617-1619.

[4] Cardinal M,Meunier J,Soulez J,et al.Intravascular ultrasound image segmentation:a three-dimensional fast-marching method based on gray level distributions[J].IEEE transactions on medical imaging,2006,25(5):590-601.

[5] 孙秋红.超声造影在产科应用中的研究进展[J].广东医学,2014,35(11):1798-1800.

[6] 陈慧贞,赵萍,贾节,等.三维超声测量斑块体积的临床应用价值[J].中国超声医学杂志,2015,31(2):110-112.

[7] Yongjian Yu,Scott T Acton,Soulez J,et al.Speckle reducing anisotropic diffusion[J].IEEE Trans Image Process,2002,11(11):1260-1270.

[8] Aja-fernandez S,Alberola-lopez C.On the estimation of the coefficient of variation for anisotropic diffusion speckle filtering[J].IEEE Trans Image Process,2006,15(9):2694-2701.

[9] Black M,Sapiro G,Marimont D,et al.Robust anisotropic diffusion[J].IEEE Trans Image Process,1998,7(3):421-432.

[10] Tauber C,Batatia H,Ayache A.robust speckle reducing anisotropic diffusion[C]//Proceedings of the 2004 International Conference on Image Processing,2004.Singapore,ICIP 2004:247-250.

[11] Xiaoming Liu,Jun Liu,Xin Xu.A robust detail preserving anisotropic diffusion for speckle reduction in ultrasound images[J].BMC Genomics,2011,12(S5):1-10.

[12] 王常虹,陈韬亦,屈桢深.使用中值-各向异性扩散的超声图像去噪算法[J]. 哈尔滨工程大学学报,2011,32(3):314-321.

[13] 李灿飞,王耀南,肖昌炎,等.用于超声斑点噪声滤波的各向异性扩散新模型[J].自动化学报,2012,38(3):412-418.

[14] 陈婷婷,沈民奋,杨金耀.一种复合各向异性扩散的图像去噪算法[J].数据采集与处理,2014,29(5):757-763.

[15] Qingling Sun,John A Hossack,Jinshan Tang,et al.Speckle reducing anisotropic diffusion for 3D ultrasound images[J].Computerized Medical Imaging and Graphics,2004,28(8):461-470.

[16] Jinshan Tang,Qingling Sun.Society of Photo-Optical Instrumentation Engineers Proceedings:Three-Dimensional Imaging Metrology,2009[C].San Jose,California,2009.

[17] Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Trans Patt Anal Mach Intell,1990,12(7):629-639.

ROBUST ANISOTROPIC DIFFUSION ALGORITHM FOR 3D ULTRASOUND IMAGES DENOISING

Luo Keyang Liu Jun

(CollegeofComputerScienceandTechnology,WuhanUniversityofScienceandTechnology,Wuhan430081,Hubei,China)

We proposed a new anisotropic diffusion filtering algorithm for 3D ultrasound images denoising. It filters the speckle noises better while preserving image’s edges and details mainly by modifying diffusion coefficient and instantaneous coefficient of variation (ICOV) in conventional algorithm. Compared with conventional algorithm, the algorithm has lower sensitivity and better robustness on the number of iterations.

3D ultrasound image Anisotropic diffusion Speckle reduction Robustness

2015-07-13。国家自然科学基金项目(31201121)。骆科扬，本科生，主研领域：图像处理。刘俊，副教授。

TP3

A

10.3969/j.issn.1000-386x.2016.11.032