基于线性解码和深度回归预测的图像分类算法

张 鸿 伍 萍

1(武汉科技大学计算机科学与技术学院 湖北 武汉 430065)2(武汉科技大学智能信息处理与实时工业系统湖北省重点实验室 湖北 武汉 430065)3(武汉大学软件工程国家重点实验室 湖北 武汉 430072)



基于线性解码和深度回归预测的图像分类算法

张 鸿1，2，3伍 萍1

1(武汉科技大学计算机科学与技术学院 湖北 武汉 430065)2(武汉科技大学智能信息处理与实时工业系统湖北省重点实验室 湖北 武汉 430065)3(武汉大学软件工程国家重点实验室 湖北 武汉 430072)

针对图像分类研究中的分类器输入范围限制和缩放问题，提出一种基于线性特征解码和深度回归模型图像分类算法。首先，通过线性解码器学习低分辨率图像的特征参数；然后，运用学习到的特征对原始高分辨率图像进行卷积和池化操作，得到特征矩阵；再通过Softmax回归模型对图像进行深度学习和分类；最后用距离度量算法得到图像分类结果。实验结果从多方面对比和验证了该方法在分类效率方面超越了传统的误差反向传播算法BP和K最近邻分类算法KNN。

线性解码器 回归模型 深度神经网络 图像分类

0 引 言

随着互联网技术和多媒体技术的蓬勃发展，以及社交媒体的日益普及和流行，人们接触到的多媒体数据也呈现出直线增长的趋势。图像数据在多媒体数据海洋中占据了十分重要的位置，它也逐步成为人们信息交流、经验分享中的重要媒介。然而，在这些网络资源库中，大部分的图像数据是没有任何文本标注的，如果单纯依靠手工标注的方式对这些纷繁复杂的图像进行分类和管理，则存在费时费力、效率低的问题。于是，如何采用合理的计算机图像分析方法，进行高效的自动分类、管理及使用，一直是图像信息处理领域的研究热点[1-5]。

一图胜千言，图像的底层特征和高层语义之间存在着难以逾越的语义鸿沟[6]。为此，许多研究者提出了基于机器学习、统计分析的解决方法以缩小语义鸿沟，可成功应用于提高图像分类的准确率。例如：文献[7]采用误差反向传播算法BP，在底层特征的基础上运用机器学习的理论来得到图像的抽象表示。但是，这种方法容易陷入局部最小值，难以达到最优的学习效果，对复杂函数的表示能力有限，不能有效针对多重的分类问题进行泛化。针对这些问题，Hinton在2006年提出了第三代神经网络[8]，即：深度学习方法。该方法可以通过学习一种深层非线性网络结构来实现复杂函数逼近，展现出较为强大的从大量样本集中学习数据集本质特征的能力[9]。例如：文献[10]采用卷积神经网络CNN获取图像的特征，并构成一幅特征映射图来对图像进行分类；但这种方法需要收集大量有标记的图像样本来训练，对训练集的要求比较高。考虑到标记样本有限的问题，Poultney等运用未标记样本集学习得到了图像的特征表达关系[11]；Le等采用基于稀疏自编码的神经网络从图像中建立其高层次的特征检测器[12]，采用无监督的反向传播方法，使目标值等于输入值，但该算法需要对输入进行限制或者缩放，使输入值在[0,1]的范围内。然而，目前关于数据范围的优化取值还属于开放性问题。

针对数据输入范围的限制和缩放问题，本文提出了基于线性解码器的深度神经网络方法，本文算法的流程如图1所示。先从原始的大图像中随机选择小块的图像区域，然后通过线性解码器学习到小图像的特征参数，并将其运用到对原始大图像的卷积和池化操作中，得到特征矩阵。在此基础上，进行Softmax回归分类和结果优化，与传统的基于向量模型的特征相似度度量模型相结合，提出了相应的自动分类机制。该网络包含输入层、隐藏层和输出层，并且无需对输入数据进行限制或缩放，简化了神经网络训练的复杂度，提高了数据预处理的效率。

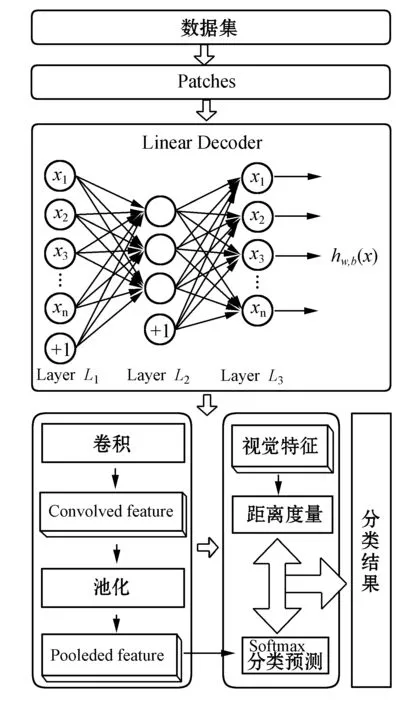
图1 本文算法流程图

1 基于线性解码的卷积特征分析

底层特征分析一直是影响图像语义理解和分类效率的关键因素。本节采用基于线性解码器的神经网络进行图像的特征学习，再利用学习到的参数在训练集及测试集中进行卷积特征分析，以及池化操作得到图像特征矩阵。

1.1 图像特征的线性解码算法分析

受深度学习中稀疏自编码方法[12,13]的启发，本文提出一种基于线性解码器的神经网络方法。神经网络方法是模拟人类神经网络中的特性，即人类大脑中的神经元细胞在接受刺激后会变的活跃，并在相互之间传递信息；通过设置网络中的每一层的节点个数，即：神经元个数，在神经网络的各个层次中传递图像特征数据，在达到收敛阈值或者最大迭代次数时，实现图像本质特征的智能学习。模拟过程如图1所示，LayerL1为输入层，接受到输入信息以后该层的神经元被激活，处理信息后传递至LayerL2层，即：隐藏层；隐藏层的神经元被激活并将处理之后的信息传递至LayerL3层，即：输出层；输出层神经元接受信息以后，输出该层处理后的结果。

假设集合X={x1,x2,x3,…,xi,…,xm}表示未标记的图像训练数据集，其中，xi表示输入的第i幅图像，m表示未标记的图像数据集样本的数量。向量Y={y1,y2,y3,…,yi,…,ym}表示输入为X时，图像集合所对应样本标记的期望输出值，其中，yi表示输入为第i幅图像时的期望输出值。本节在已有未标记的图像样本集X的基础上，生成一个假设模型hw,b(x)，表示输入为x时的假设输出，其中，w为权值向量，b为偏置向量。特征学习的过程就是求解向量w和向量b。

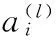
(1)

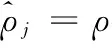
(2)

其中，第一项为均方差项，第二项为防止过度拟合添加的权重衰减项。nl表示网络层数，λ为权重衰减参数，第三项为稀疏性控制的惩罚项，β为控制稀疏性惩罚因子的权重。

(3)

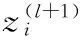
1.2 基于部分联通网络的卷积特征分析

由于神经网络方法需要训练网络中神经元的权值向量w和偏置向量b，而向量w和b的个数则取决于图像分辨率的大小[8]。图像的分辨率越大，网络需要学习的向量个数越多。可见，图像分辨率的大小直接影响参数学习的复杂度。

为此，本节提出基于部分联通网络的卷积算法，即：将图像训练集中初始的图像样本全部切分成若干个小区域，构成区域子集，作为神经网络的输入层，也相当于在原有全联通网络基础上，使隐藏层神经元只连接输入层的一部分神经元。通过该算法得到数据集卷积后的特征矩阵，将该矩阵作为图像分类器的输入。

假设集合Ω={(z1,r1),(z2,r2),…,(zi,ri),…,(zt,rt)}表示有标记的图像训练集样本，其中t用来表示已标记的训练集样本个数，并假设标记样本集Ω中的图像属于k个不同的类别，zi表示训练集中的第i幅标记样本图像，ri表示该图像所属的类别编号。假设未标记的图像测试集用S={s1,s2,…,si,…,sn}表示，其中si表示测试集中的第i幅图像，n表示测试集样本个数。假设数据集Ω和S中图像的分辨率为a×a，从中随机选取一块分辨率为b×b的一个局部小块图像。将选取的所有局部小块图像数据集X={x1,x2,x3,…,xi,…,xm}作为线性解码器的输入，如图1中Pathes所示。

根据1.1节的特征学习算法计算出权值向量w和偏置向量b，设置卷积运算的步长为1，并利用从X={x1,x2,x3,…,xi,…,xm}中学习到的参数值对训练集Ω以及测试集S进行卷积运算。则在训练集Ω和测试集S上完成卷积后的特征矩阵分别为DConvoled_Train、DConvoled_Test，其维数大小均为为：

k×(a-b+1)×(a-b+1)

(4)

其中，k为隐藏层中的神经元个数。可见，矩阵DConvoled_Train和DConvoled_Test的维数非常高，不利于训练分类器，很容易出现过拟合的现象，影响图像分类效率。为此，本文采用计算图像各个区域上的特定特征的平均值方法对图像不同位置的特征进行聚合统计，即：池化操作。设定池化区域的大小为Dpooling，且池化操作必须作用于不重复的区域内，则可得到池化后的特征矩阵DPooled_Train和DPooled_Test。

2 基于卷积特征的回归预测

根据第1节中得到的训练集Ω与测试集S图像的特征矩阵DPooled_Train和DPooled_Test，采用改进的Softmax深度回归预测模型进行初步分类，并结合图像的视觉特征，学习得到测试集S中未标记样本si所属的语义类别。

2.1 回归函数定义和参数求解

将训练集图像的特征矩阵DPooled_Train作为该模型的训练样本，对于每一个输入的样本(zi,ri)，该模型预测其每一种分类结果出现的概率值为p(ri=k|zi)，假设函数定义如下：

(5)

其中，θ1,θ2,…,θk是该模型的训练参数。定义函数hθ(zi)求解的代价函数为：

(6)

其中1{ri=j}为指示性函数，当ri=j为真时，1{ri=j}=1，反之1{ri=j}=0。为了防止模型中参数的冗余，在代价函数J(θ)中加入权重衰减项：

(7)

进一步，求其偏导数为：

(8)

通过迭代得到J(θ)的最小值，求出参数θ1,θ2,…,θk，得到训练好的Softmax回归模型。然后运用该模型来对测试集S进行分类，通过式(5)计算出每一个样本在每一个类别中的概率值。

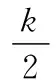
(9)

2.2 未标记测试样本的分类方法

在未标记的图像训练集X中，除了通过基于线性解码器的神经网络学习到的特征DPooled_feature，还可以提取图像的视觉特征。由于2.1节只是对测试集中的每个样本进行了初步预测，本节在预测标签集合Ci的基础上，在视觉特征空间中采用距离度量的算法确定最终的预测标签。

设从图像训练集和测试集中所提取的图像视觉特征的维数均为p，在包含m个有标记图像的训练集Ω上可得到视觉特征矩阵A∈m×p。同时在包含n个未标记图像的测试集Ε上得到视觉特征矩阵B∈n×p。设zi、sj分别表示矩阵A、B中的任意一个训练样本和一个测试样本的特征向量，它们之间的距离记为dij，选择欧式距离作为zi和sj的距离度量。

在2.1节中，已经完成了对图像的初步分类，因此，在计算样本间的距离时，只计算测试样本与预测类别Ci中包括的类别的距离。然后，取dij最小值所对应样本的类别作为最终的测试样本sj的预测结果，记为Li，完成图像的分类。整个算法流程如算法1所示。

算法1 基于线性解码和回归预测的图像分类算法

3 实验结果与分析

3.1 数据集与特征提取

为了验证上述算法的性能，本文选取了两组图像数据集进行测试和验证。首先，从Web页面采集了10个语义类别的图像作为数据集，包括：鸟、马、小狗、海豚、大象、爆炸、飞机、摩托车、汽车、溪水。其中每个类别包含100幅图像，从中选取700幅图像作为训练集，其余300幅图像作为未标记的测试集。此外，还使用了公共图像数据集MSRA-MM[19]进行了实验验证，从MSRA-MM数据库中选取了6000幅图像作为训练集，其余3000幅作为测试集。图2显示了10个语义的Web图像数据的示例，其中每一列表示从一个语义类别中随机抽取的3幅图像样本。此外，实验提取的底层视觉特征包括256-d HSV颜色直方图、64-d LAB颜色聚合向量以及32-d Tamura方向度。

图2 Web数据集样本示例

3.2 实验结果与分析

首先将Web数据集和MRSA-MM数据集中图像尺寸进行归一化，统一为96×96。同时，将用于1.1节中网络学习的小图像尺寸设定为8×8，且从每幅图像中提取100幅小图像，再从所有提取的小图像中随机选取100 000个样本作为线性解码器的输入。由于图像为彩色图，需要将三个通道的值同时作为输入层，则输入层的神经元个数为8×8×3，即192个；同样，输出层神经元个数也为192个，且设置隐藏层的神经元个数为400个，学习得到400个特征，如图3所示。图中每个小块图像表示所对应的隐藏层神经元学习到的特征值的可视化表示，可以观察到，很多小块都是类似图像的边缘部分，这有利于进行边缘检测来识别图像。同时，设置池化区域Dpooling的尺寸为19×19。

图3 学习得到的400个隐藏层神经元特征

为了验证本文方法的有效性和优越性，选取隐藏神经元为400个的传统BP神经网络、Softmax分类、KNN分类算法，并使用精确率ACC(accuracy)作为评价指标。实验结果如表1所示。

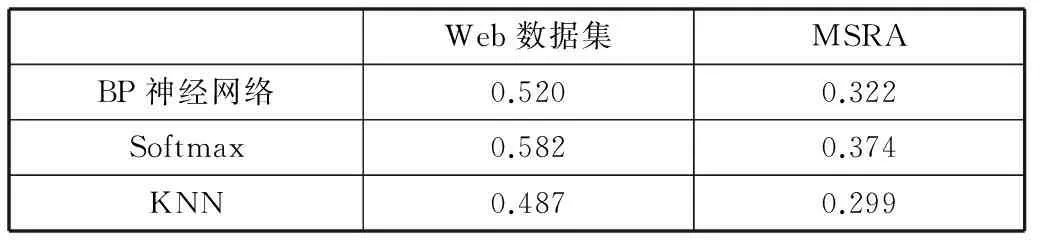
表1 不同算法在MSRA和WEB数据集上的ACC性能比较

从表1可以看出，在隐藏层神经元数目相同的情况下，采用Softmax分类方法的性能高于传统BP神经网络10.7个百分点。在确定分类方法后，为验证本文方法的有效性和优越性，实验分别采用下列三种距离度量方法，即：欧氏距离度量(Euclidean Distance)、马氏距离度量(Mahalanobis Distance)、夹角余弦(Cosine)距离度量，与本文的方法进行对比实验，并使用精确率ACC(accuracy)作为评价指标，实验结果如表2所示。

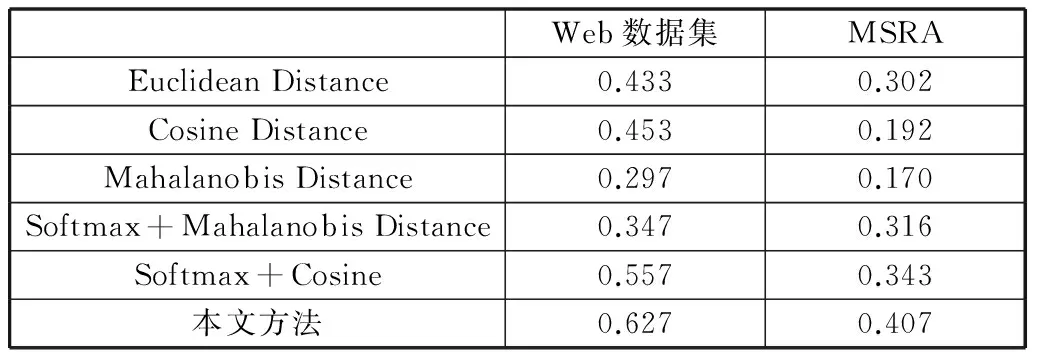
表2 不同算法在MSRA和WEB数据集上的ACC性能比较

由表2可见，相对于使用单一的距离度量算法，与Softmax分类方法相结合后的性能有显著提高。同时，本文方法在三种组合算法中的性能最优，高于Softmax+Mahalanobis Distance、Softmax+Cosine28个百分点和17个百分点。

4 结 语

本文提出的基于线性解码器的深度神经网络，并采用改进的Softmax回归模型与图像视觉特征距离度量相结合的分类算法，避免了单一使用网络学习的特征矩阵或者人工提取的视觉特征矩阵带来的分类误差。实验结果验证了本文方法在不同的图像数据集上均取得了较好的分类性能，并且明显超越了传统的图像分类方法。如何将该算法拓展到多标注或多类别图像分类中，是下一步要考虑的问题。

[1] Gudivada V N,Raghavan V V.Content based image retrieval systems[J].Computer,1995,28(9):18-22.

[2] Cavazza M,Green R,Palmer I.Multimedia semantic features and image content description[C]//Multimedia Modeling,1998.MMM’98.Proceedings.1998.IEEE,1998:39-46.

[3] He X,King O,Ma W Y,et al.Learning a semantic space from user’s relevance feedback for image retrieval[J].Circuits and Systems for Video Technology,IEEE Transactions on,2003,13(1):39-48.

[4] Han D,Li W,Li Z.Semantic image classification using statistical local spatial relations model[J].Multimedia Tools and Applications,2008,39(2):169-188.

[5] Zhang Q,Izquierdo E.Multifeature analysis and semantic context learning for image classification[J].ACM Transactions on Multimedia Computing,Communications,and Applications (TOMCCAP),2013,9(2):12.

[6] Michael S Lew,Nicu Sebe,Chabane Djeraba,et al.Content-based multimedia information retrieval:State of the art and challenges[J].ACM Transactions on Multimedia Computing,Communications,and Applications (TOMM),2006,2(1):1-19.

[7] Cigizoglu H,Kisi O.Flow prediction by three back propagation techniques using k-fold partitioning of neural network training data[J].Nordic Hydrology,2005,36(1):49-64.

[8] Hinton G E,Salakhutdinov R R.Reducing the dimensionality of data with neural networks[J].Science,2006,313(5786):504-507.

[9] Sun Z J,Xue L,Xu Y M,et al.Overview of deep learning[J].Jisuanji Yingyong Yanjiu,2012,29(8):2806-2810.

[10] Krizhevsky A,Sutskever I,Hinton G E.Imagenet classification with deep convolutional neural networks[C]//Advances in neural information processing systems.2012:1097-1105.

[11] Poultney C,Chopra S,Cun Y L.Efficient learning of sparse representations with an energy-based model[C]//Advances in neural information processing systems.2006:1137-1144.

[12] Le Q V.Building high-level features using large scale unsupervised learning[C]//Acoustics,Speech and Signal Processing (ICASSP),2013 IEEE International Conference on.IEEE,2013:8595-8598.

[13] Hinton G E.Learning multiple layers of representation[J].Trends in cognitive sciences,2007,11(10):428-434.

[14] Hinton G E.Training products of experts by minimizing contrastive divergence[J].Neural computation,2002,14(8):1771-1800.

[15] Rifai S,Vincent P,Muller X,et al.Contractive auto-encoders:Explicit invariance during feature extraction[C]//Proceedings of the 28th International Conference on Machine Learning (ICML-11).2011:833-840.

[16] Li C H,Ho H H,Kuo B C,et al.A Semi-Supervised Feature Extraction based on Supervised and Fuzzy-based Linear Discriminant Analysis for Hyperspectral Image Classification[J].Appl.Math,2015,9(1L):81-87.

[17] Bengio Y,Courville A,Vincent P.Representation learning:A review and new perspectives[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2013,35(8):1798-1828.

[18] Dong Z,Pei M,He Y,et al.Vehicle Type Classification Using Unsupervised Convolutional Neural Network[C]//Pattern Recognition (ICPR),2014 22nd International Conference on.IEEE,2014:172-177.

[19] Li H,Wang M,Hua X S.MSRA-MM 2.0:A large-scale web multimedia dataset[C] //Proceedings of the 2009 IEEE International Conference on Data Mining Workshops,Washington,2009:164-169

[20] Akata Z,Perronnin F,Harchaoui Z,et al.Good practice in large-scale learning for image classification[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2014,36(3):507-520.

[21] Abdelbary H A,ElKorany A M,Bahgat R.Utilizing deep learning for content-based community detection[C]//Science and Information Conference (SAI),2014.IEEE,2014:777-784.

[22] Ciresan D,Meier U,Schmidhuber J.Multi-column deep neural networks for image classification[C]//Computer Vision and Pattern Recognition (CVPR),2012 IEEE Conference on.IEEE,2012:3642-3649.

IMAGE CLASSIFICATION BASED ON LINEAR DECODING AND DEEP REGRESSION PREDICTION

Zhang Hong1,2,3Wu Ping1

1(CollegeofComputerScienceandTechnology,WuhanUniversityofScienceandTechnology,Wuhan430065,Hubei,China)2(IntelligentInformationProcessingandReal-timeIndustrialSystemsHubeiProvinceKeyLaboratory,WuhanUniversityofScienceandTechnology,Wuhan430065,Hubei,China)3(StateKeyLaboratoryofSoftwareEngineering,WuhanUniversity,Wuhan430072,Hubei,China)

Aiming at the problems of the limitation of classifier input range and the zooming in image classification research,this paper proposes an image classification algorithm which is based on linear feature decoding and deep regression model.First,we learn feature parameters of low-resolution image through linear decoder;secondly,by using the learned features we convolve and pool the primitive high-resolution image to obtain the feature matrix;thirdly,by using Softmax regression model we carry out deep learning and classification on image;finally,we obtain the classification results with distance metric algorithm.Experimental results contrast in many ways as well as verify that our method is superior to traditional error back propagation algorithm and K-nearest neighbour classification algorithm in classification efficiency.

Linear decoders Regression model Deep neural network Image classification

2015-03-09。国家自然科学基金项目(61003127,61373109);武汉大学软件工程国家重点实验室开放基金项目(SKLSE2012-09-31)。张鸿，教授，主研领域：多媒体分析与检索，统计学习，机器学习。伍萍，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2016.11.031