CoSaMP改进算法在信道估计中的应用

任晓奎 刘星宇

(辽宁工程技术大学电子与信息工程学院 辽宁 葫芦岛 125105)



CoSaMP改进算法在信道估计中的应用

任晓奎 刘星宇*

(辽宁工程技术大学电子与信息工程学院 辽宁 葫芦岛 125105)

压缩采样匹配追踪CoSaMP(Compressive Sampling Matching Pursuit)算法作为压缩感知中信道估计比较具有代表性的算法之一，一直无法解决如何获取信道的稀疏度问题。为了解决该问题，提出一种利用峰值信噪比PSNR同迭代次数之间的关系而构造的一种改进算法。该算法可以自适应确定迭代次数，从而有效地提高CoSaMP算法的效率，增加了CoSaMP算法在实际信道估计中的可行性。

压缩采样匹配追踪 压缩感知 信道估计 峰值信噪比

0 引 言

压缩感知CS技术[1-3]作为一个新兴的采样技术，与传统奈奎斯特(Nyquist)采样理论[4]不同，其根据实际环境中信号通常是稀疏的性质，可以利用远远小于传统Nyquist的采样率通过随机采样最终重构出较为完整的信号。压缩感知技术应用领域广泛，在无线通信、图像处理、光学成像术、天文学等领域[5]均有压缩感知技术的身影。

近年来，压缩感知技术开始在信道估计领域中被广泛研究。传统的信道估计技术如最小二乘[6](LS)法和最小均方误差[7](MMSE)法均是对信道是密集型的假设，其需要利用大量的导频信号对信道做出估计。但近年来的大量研究表明，在实际环境中信号往往是稀疏的，所以对传统的信道估计算法来说，由于利用大量的导频信号，使导频利用率大大降低。压缩采样匹配追踪[8-10]CoSaMP算法作为一种贪婪算法，具有较好的鲁棒性，并且通过利用少量的导频信号就可以恢复出较为精确完整的信号。但由于CoSaMP算法的使用必须先知道稀疏度K，所以导致该算法在实际信道估计中存在局限性。本文提出的算法通过限制等距性质推导出峰值信噪比和迭代次数的关系，从而使CoSaMP算法可以自适应地确定迭代次数，提高算法的可行性。

1 压缩感知技术

压缩感知是近年来极为热门的研究前沿，该技术在若干应用领域中都引起了极大的关注。压缩感知技术的基本原理为：已知将要获取的未知信号为f，假设f是不连续的、稀疏的，那么当获取信号f时由于未知信号f为稀疏的，所以就不需要对原始信号的每个分量进行测量。假设原始信号的维数为M，那么只需要用远远小于M的导频信号个数就能恢复原始信号f。CS理论的本质是通过对信号的高度不完备线性测量的精确重建，可以通过抽样保留其中最有用的系数。如果想通过抽取少量的数据就能恢复大量的信息，必须要满足以下两点：(1)抽取的数据里面含有信号的全局信息;(2)存在算法利用少量的信息就可以恢复出原有的信号，同时如果要保证在抽取过程中不会丢失重要信号，其恢复信号的观测矩阵必须满足有限等距性质[11，12](RIP)，即：

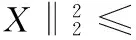
该性质保证了观测矩阵不会把两个不同的K稀疏信号映射到同一个集合中(保证原空间到稀疏空间的一一映射关系),其要求从观测矩阵中抽取的每M个列向量构成的矩阵是非奇异的。

目前，压缩感知技术应用在信道估计领域中常常使用迭代的贪婪算法，如OMP[13-16]、SAMP[17-20]以及CoSaMP算法等。接下来将对CoSaMP算法进行改进并做出说明。

2 算 法

2.1 传统信道估计算法

传统的信道估计以最小二乘法(LS)和最小均方误差法(MMSE)两种算法最具代表性。其中，MMSE算法信道估计精度很高，但其算法复杂，需要大量的矩阵运算，计算量大；LS算法具有结构简单、计算量小的特点。但以上两种传统算法均是基于信道为密集型的假设，没有考虑到真实信道具有潜在稀疏性的特性，导致其利用比实际信道变量更多的导频信号才能准确对信道做出估计，从而导致了频谱利用率的降低。

2.2 CoSaMP算法

CoSaMP算法是一种贪婪算法[21]，其通过反复的迭代从矩阵中选出n列最优集合，然后再估计出最优值。具体步骤如下：

已知稀疏度K、观测值y、迭代次数为n、发射导频Z。

(1) 令迭代次数n=1、候选集M=φ、首次残差r0=y、x0=0。

(2) 找到2K列与残差最为相关的向量组成集合Ω。

(3) 将上一步得出的集合Ω与Mn-1作并集，即：

H=Mn-1∪Ω

(4) 用最小二乘法(LS)在H中做信道估计,保留其中最大的k个系数。

(5) 更新残差值：r=y-Z·xn。

(6) 判断是否满足迭代条件，不满足则n=n+1，跳到步骤(2)重新计算，满足则输出X的值。

由以上的步骤可知，CoSaMP算法的实现必须依赖其稀疏度K为已知的[22]。而在实际的信道估计当中，稀疏度K的值是很难获取的，所以该算法在实际的信道估计应用中的意义大大降低。

2.3 改进的CoSaMP算法

首先要通过PSNR值的变化趋势，来确定迭代的次数，PSNR值的公式如下：

(1)

式中MAX指的是8 bit表示法的最大值为255，MSE为均方误差，所以式(1)可以转化成下式：

(2)

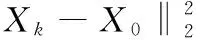
(3)

已知RIP性质：

(4)

假设X1、X2均满足上式，则：

将上面两式联立变换得出下式：

将不等式右边去掉，左侧整理得：

(5)

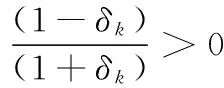
由于CoSaMP算法在实际应用中必须使迭代次数和稀疏度K保持一致才可以精确获得重构信号，通过式(3)的转换，假设第k次迭代和第k+1次迭代的判别式分别为Pk和Pk+1，即：

(6)

(7)

则Pk和Pk+1的相对差值为：

(8)

其中：ΔP=Pk+1-Pk+1。

PSNR值会随着迭代次数K的增加而缓慢增加，此时相对差值dk<0。而当迭代次数K超过某一门限值时，PSNR值会突然剧烈下降，同时，相对差值dk值会急剧上升，并随着迭代次数的增加又迅速回归到0附近。利用该性质可以通过设定一个门限阈值来确定迭代的次数。

所以改进的重构算法如下：

(1) 令迭代次数n=1、候选集M=φ、首次残差r0=y、x0=0、门限值为μ。

(2) 找到2K列与残差最为相关的向量组成集合Ω。

(3) 将上一步得出的集合Ω与Mn-1作并集，即：

H=Mn-1∪Ω

(4) 用最小二乘法(LS)在H中做信道估计保留其中最大的k个系数。

(5) 更新残差值：r=y-Z·xn。

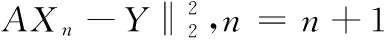
(7) 迭代完成后判断相对差值dn>μ是否成立，成立就停止迭代，反之就跳到步骤(2)重新执行。

以上即为CoSaMP的改进算法[23，24]。该算法通过计算dn的值并设置合理的阈值μ的方法来确定迭代的次数，通过该算法可以有效地提高重构信号的质量。

3 实验仿真与验证

为了证明改进后的CoSaMP算法相比其他算法的优越性，本文对OMP算法、CoSaMP算法以及改进算法进行实验仿真。仿真硬件为Intel(R) Core(TM) i7-4500U CPU，主频1.80 GHZ，内存8 GB，Microsoft Windows 7操作系统，仿真软件为MATLAB。

假设天线方案为2根发射天线和2根接收天线，系统子载波个数为1024，信道长度为25，非零抽头的个数为5个，并且系统参数在一个OFDM符号内保持不变。可以通过算法的归一化均方误差(MSE)反映算法的估计性能，MSE计算公式为：

(9)

MSE值的大小说明了算法性能的好坏，MSE值越小说明算法估计的误差越小，算法的性能越好。

图1显示了在不同导频数目下各个算法的MSE的大小情况。由图1可以看出，随着导频数目的增加，各个算法的MSE值均有下降的趋势。在导频数目相同的情况下，OMP算法的MSE值最大，性能最差，CoSaMP算法次之；而改进算法的MSE值小于其他两种算法，其性能优与OMP算法和CoSaMP算法。

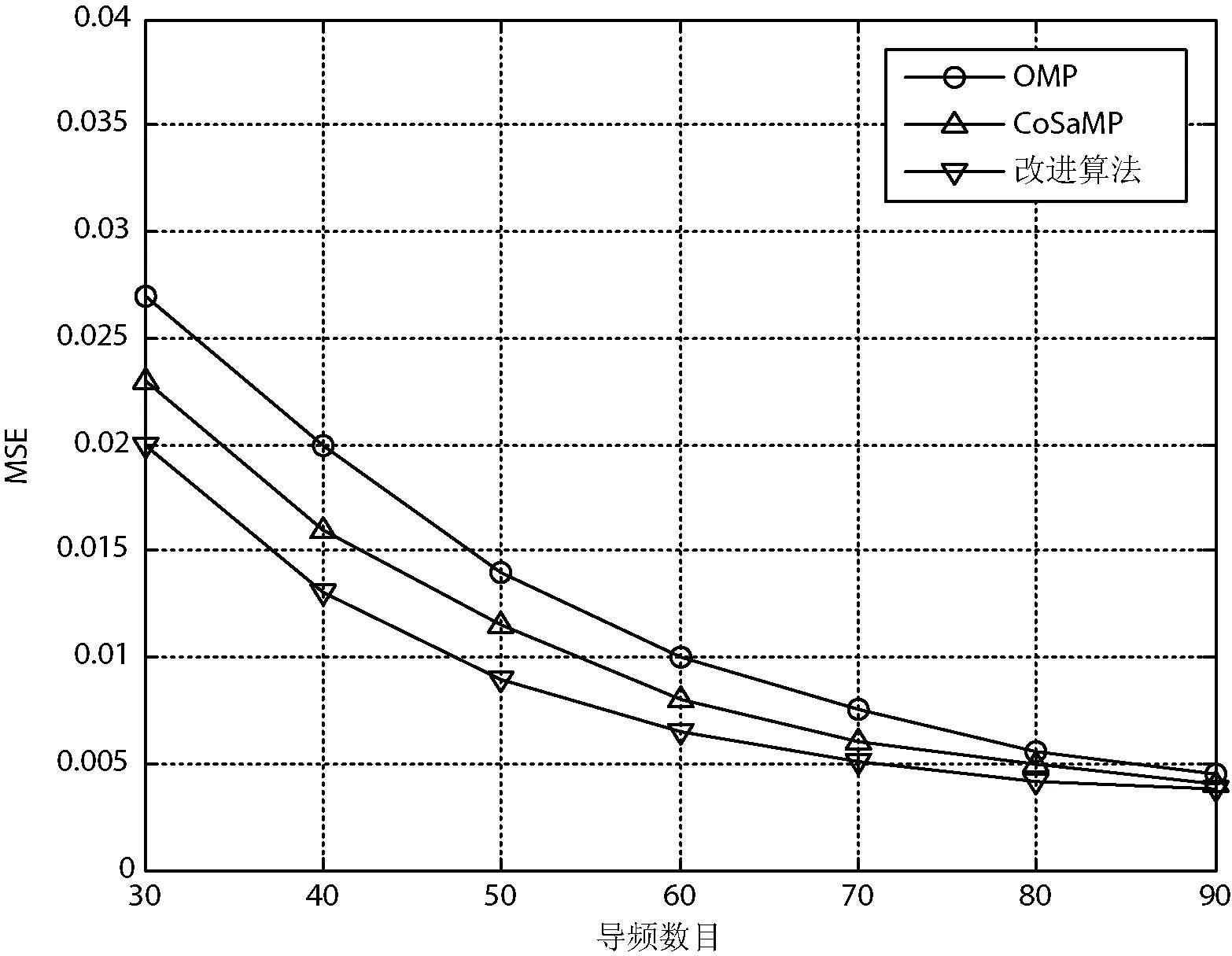
图1 不同导频数目下各算法MSE性能比较

图2显示了各个算法在不同信噪比下的MSE值的情况，信噪比越小说明信号的干扰越大。在信噪比相同时，算法的MSE值越小说明算法的抗干扰能力越强。在图2中可以看到，三种算法随着信噪比的增大，MSE值均呈下降趋势，但改进的CoSaMP算法相比其他两种算法具有更小的MSE值。

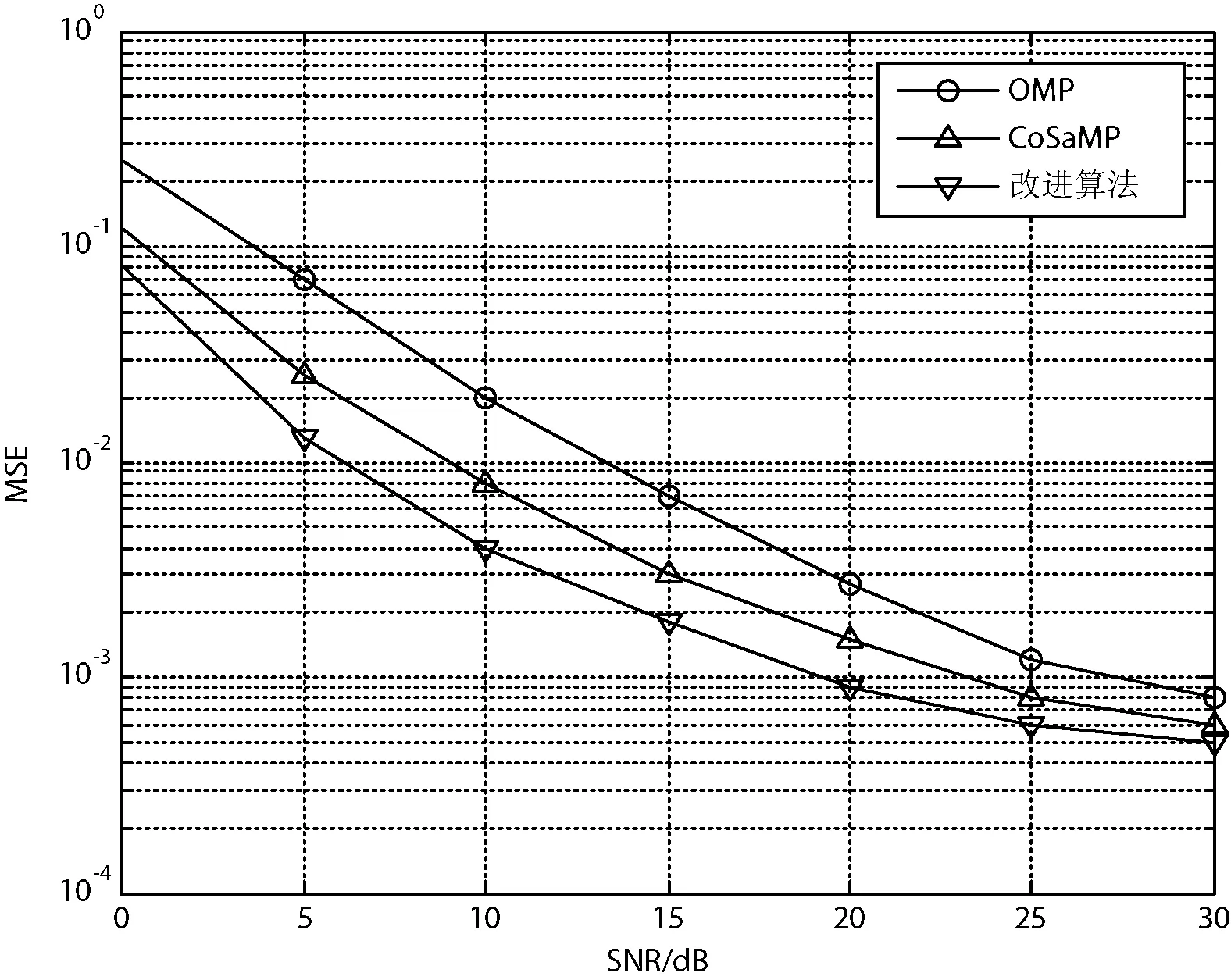
图2 不同信噪比下各算法MSE性能比较

图3显示的是在不同信噪比下三种算法的误比特率(BER)值的大小情况。随着信噪比的增大，信号干扰减少，各个算法的BER均呈下降趋势，其中OMP算法的BER值最大，CoSaMP算法次之。改进算法在三种算法中的BER值最小，说明改进后的算法相比其他两种算法有着更好的性能。

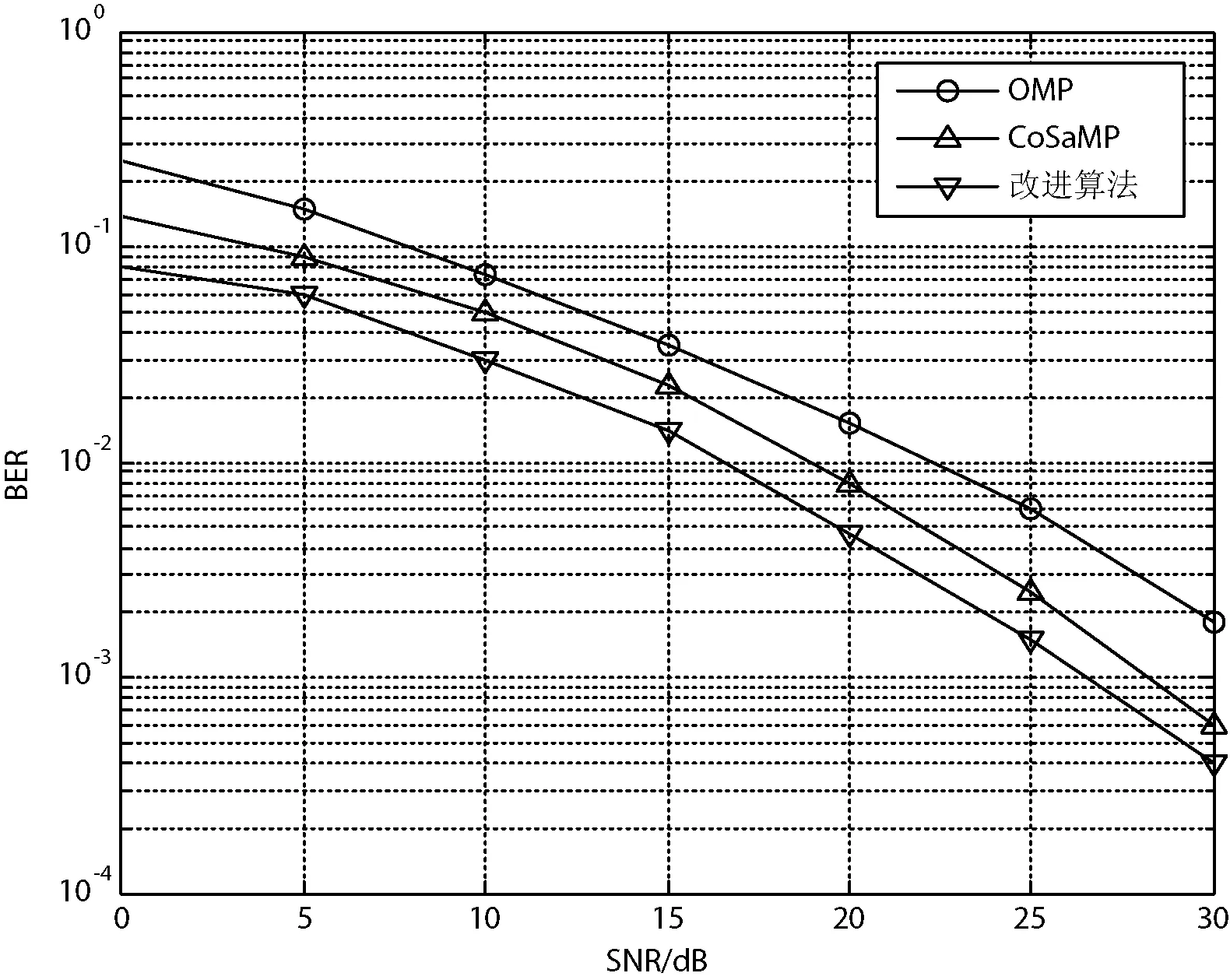
图3 不同信噪比下各算法的BER性能比较

在实际应用过程中，重构信号时所需要的时间也是需要重点考量的一个因素，所以应该在仿真中加入高斯噪声，比较三种算法所需的重构时间。

本文将高斯噪声分为0.001、0.005、0.01三个等级，分别在稀疏度K=15和K=25时对OMP算法、CoSaMP算法和改进后的CoSaMP算法的重构时间进行比较。

由表1和表2看出，当σ2=0.01时OMP算法已经不能完成重构，说明CoSaMP算法和改进的CoSaMP算法相比OMP算法有着更好的抗干扰能力。在相同的噪声等级下，改进算法相比CoSaMP算法需要更多的重构时间。这是因为要想确定合理的迭代次数，并提高信号重构的精确程度，势必会增加运算量。但两种算法相差的运算时间仍在一个数量级可接受的范围之内，所以在实际应用中，改进的CoSaMP算法相比CoSaMP算法有着更大的应用意义。

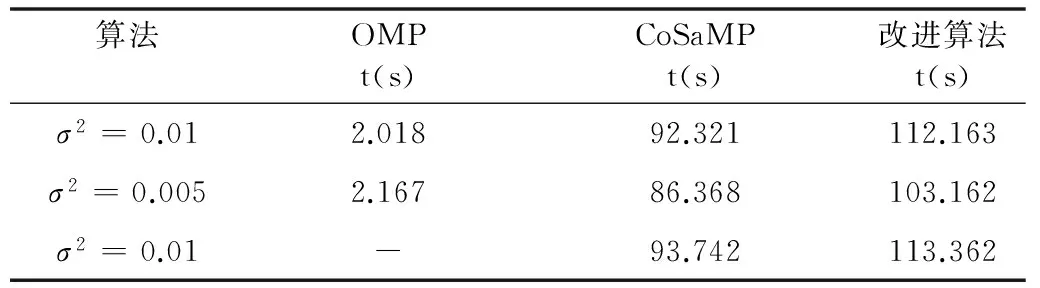
表1 k=15时各算法重构时间与误差

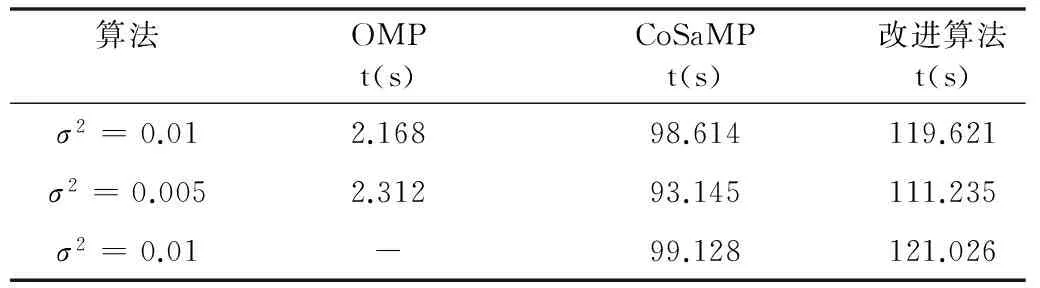
表2 k=25时各算法重构时间与误差

4 结 语

本文根据MIMO-OFDM信道特性，基于压缩采样改进匹配追踪算法的MIMO-OFDM信道估计，提出了一种根据PSNR的增减趋势来判断CoSaMP算法迭代次数的改进算法。该算法和传统的CoSaMP算法相比无需预先知道信号的稀疏度，改进后的算法可以自适应地完成稀疏信号的重构。仿真结果表明，提出的算法有效地提高重构信号的精确程度和抗干扰能力。但是本文算法也存在着缺点，要想确定合理的迭代次数，会导致计算量的增加。如何在确保提高重构信号成功率的同时，减小确定迭代次数过程中的计算量将是下一步要研究的问题。

[1] 李然,干宗良,崔子冠,等.压缩感知图像重建算法的研究现状及其展望[J].电视技术,2013,37(19):7-14.

[2] Eldar Y C,Kutyniok G.Compressed sensing:theroy and applications[M].Combridge:Cambridge University Press,2012.

[3] Kutyniok G.Theory and applications of compressed sensing[J].GAMM-Mitteilungen，2013,36(1):79-101.

[4] Baraniuk R G.Compressive sensing Lecture Notes [J].IEEE Signal Processing Magazine ,2007,24(4):118-121.

[5] Qaisar S，Bilal R M，Iqbal W，et al.Compressive sensing：from theory to applications，a survey[J].Journal of Communications and Networks，2013,15(5):443-456.

[6] Li Ye.Simplified channel estimation for OFMD systems with multiple transmit antennas[J].IEEE Transactions on Wireless Communications,2002,1(1):67-75.

[7] Suh C,Hwang C S,Choit H.Comparative study of time-domain and frequency-domain channel estimation in MIMO-OFDM systems[C]//14th IEEE Proceedings on Personal,Indoor and Mobile Radio Communications.IEEE Press,2003,2:1095-1099.

[8] 闫鹏,王阿川.基于压缩感知的CoSaMP算法的自适应性改进[J].计算机工程,2013,39(6):28-33.

[9] Needell D,Tropp J A.CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2009,26(3):301-321.

[10] 田文飚,付争,芮国胜.基于分治试探的盲自适应匹配追踪重构算法[J].通信学报，2013,34(4):180-186.

[11] 金坚,谷源涛,梅顺良.压缩采样技术及其应用[J].电子与信息学报,2010,33(2):470-475.

[12] 路畅,刘玉红.压缩感知理论中的RIP准则[J].自动化与仪器仪表,2015(8):211-213.

[13] Do T T,Gan L,Nguyen N,et al.Sparsity Adaptive Matching Pursuit Algorithm for Practical Compressed Sensing[C]//Proceedings of the 42nd Asilomar Conference on Signals,Systems and Computers,2008:581-587.

[14] 赵龙慧,潘乐炳,李宝清.OFDM稀疏信道估计中改进的OMP算法[J].计算机工程与设计，2015,36(7):1701-1705.

[15] Donoho D L,Tsaig Y,Drori I,et al.Sparse solution of underdetermine systems of linear equations by stagewise orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2012,58(2):1094-1121.

[16] Zhao Q,Wang J K,Han Y H,et al.Compressive sensing of block sparse signals recovery based on sparsity adaptive regularized orthogonal matching pursuit algorithm[C]//2012 IEEE fifth International Conference on Advanced Computational Intelligence,2012:1141-1144.

[17] 叶新荣,朱卫平,孟庆民.基于SAMP重构算法的OFDM系统稀疏信道估计方法[J].信号处理,2012,28(3):392-396.

[18] 姜杉,仇洪冰,韩旭.基于自适应阈值SAMP算法的OFDM稀疏信道估计[J].计算机应用,2013,33(6):1508-1510,1514.

[19] 吕伟杰,陈霞,刘红珍.基于压缩感知的自适应匹配追踪优化 [J].系统工程与电子技术,2015,37(5):1201-1205.

[20] Tropp J A,Gilbert A C.Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

[21] Deanna Needell,Roman Vershynin.Uniform Uncertainty Principle and Signal Recovery via Regularized Orthogonal Matching Pursuit[J].Foundations of Computational Mathematics,2009,9(3):317-334.

[22] 张格森.压缩传感理论及若干应用技术研究[D].哈尔滨：哈尔滨工程大学,2012.

[23] 朱延万,赵拥军,孙兵.一种改进的稀疏度自适应匹配追踪算法[J].信号处理，2012,28(1):80-86.

[24] 王磊,周乐囡,姬红兵,等.一种面向信号分类的匹配追踪新方法[J].电子与信息学报,2014,36(6):1299-1306.

[25] 刘继承,王敏莹,李浩然.基于改进CoSaMP算法的图像重建[J].计算机与现代化,2015(5):48-52.

APPLYING IMPROVED COSAMP ALGORITHM IN CHANNEL ESTIMATION

Ren Xiaokui Liu Xingyu*

(SchoolofElectronicandInformationEngineering,LiaoningTechnicalUniversity,Huludao125105,Liaoning,China)

Compressive sampling matching pursuit (CoSaMP) algorithm,as one of the typical algorithms in channel estimation of compressed sensing,has not been able to solve the problem of channel sparsity acquisition.In order to solve this problem,this paper,by using the relationship between peak signal-to-noise ratio and the number of iterations,puts forward an improved algorithm.The algorithm can adaptively determine the number of iterations,so that effectively improves the efficiency of CoSaMP algorithm,and increases the feasibility of CoSaMP algorithm in actual channel estimation as well.

Compressive sampling matching pursuit Compressed sensing Channel estimation Peak signal-to-noise ratio

2015-08-07。任晓奎，副教授，主研领域：通信电路系统，无线通信信道估计。刘星宇，硕士生。

TP393.17

A

10.3969/j.issn.1000-386x.2016.11.025