HSS模型在软土地区水闸地基基础设计中的研究
2016-12-26杨永保田利勇
吴 逸,杨永保,田利勇
(1.上海戎合城市规划设计有限公司,上海 200072;2.上海市宝山区堤防水闸管理所,上海 200439;3.上海市水利工程设计研究院,上海 200061)
HSS模型在软土地区水闸地基基础设计中的研究
吴 逸1,杨永保2,田利勇3
(1.上海戎合城市规划设计有限公司,上海 200072;2.上海市宝山区堤防水闸管理所,上海 200439;3.上海市水利工程设计研究院,上海 200061)
阐释了近年来岩土有限元分析中常用的土体本构模型HS模型及HSS模型的理论依据,探讨其参数选择办法,以某位于上海市杭州湾南岸水闸为例,同时采用HS模型与HSS模型进行了有限元分析计算,并与实测监测数据展开对比,通过计算结果对比表明HSS模型模拟结果与工程建设过程中监测成果更为吻合,说明HSS模型可以更好的模拟边载、地基基础及上部结构之间相互作用,可以指导水闸工程复杂地基基础的优化设计。
HSSPlaxis;水闸;软土;有限元分析
1 概述
近年来,计算机技术和有关有限元分析软件又有了较大发展,结构、土体和水体三者共同作用下的稳定性和变形分析已经成为关注的重点。其中,岩土本构模型始终是有限元分析的核心。从早期的摩尔库伦模型(MC)到后来的邓肯张模型,再到后来的HS 模型(Hardening Soil Model)与HSS模型(Hardening Soil Small-train Model),它们不断提升工程分析中的精度,但没有哪一种本构模型能全面的、正确的模拟任何一类土体在任意加载下的土体性质,如何能更为准确的模拟软土地基中荷载、基础与地基之间的相互作用,选用更符合水利工程特点及软土特性的土体本构模型,是工程分析研究中的要点和难点。
本文将借助PLAXIS岩土有限元软件,以上海市某水闸为例,分别采用HS模型与HSS模型进行有限元模拟分析,并将结果与实测监测数据进行对比,以研究更为准确的土体本构模型和参数取值。
2 HSS本构模型
2.1 HS模型
Schanz和Schanz等在 Vermeer的双硬化模型的基础上进行改善并提出了HS 模型(Hardening Soil Model),该模型在模拟土体剪切方面可认为是弹塑性的Duncan-Chang 模型,考虑了土体的剪胀性及加载模量与卸荷模量之间的差异。HS模型加入了塑性理论,考虑了在主应力空间中屈服面的不确定,由一个双曲线型的剪切屈服面以及一个椭圆型的盖帽屈服面组成,且其盖帽屈服面可模拟土体体积压缩方面的特性,见图1。
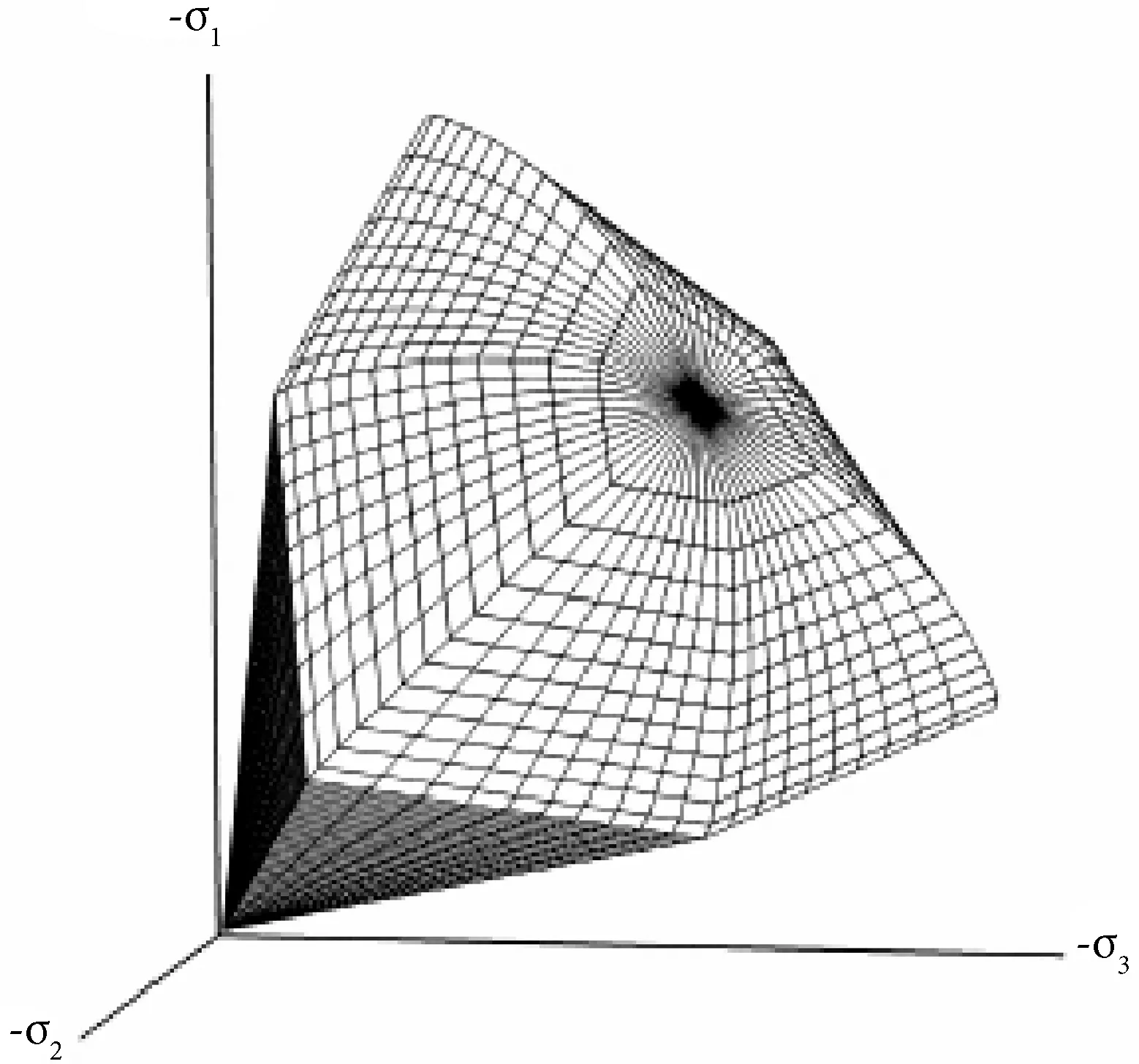
图1 HS模型的屈服盖帽
2.2 HSS模型
小应变硬化模型理论则进一步考虑了土体剪切刚度与应变的非线性关系。根据土体实测试验结果,可获得典型的剪切刚度-应变的关系,如图2所示,剪切刚度在应变增大过程中呈“S”形衰减,在常规三轴试验中,固结试验测得的刚度小于初始刚度的1/2。

图2 土体剪应变——剪切刚度的关系
HSS模型与HS模型两者有着几乎相同的计算参数,只增加了两个参数用于描述小应变刚度行为:初始小应变模量G0;剪切应变水平γ0.7:割线模量Gs减小到70%G0是的应变水平。为了能更好的描述小应变区域内剪切刚度与应变之间的双曲线关系,HSS模型采用了Hardin-Drneveich模型的计算方法,计算公式可描述如下:
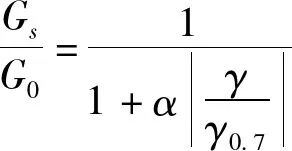
参考Benz(2007)的相关文献,在PLAXIS中假定卸载及重加载时的泊桑比vur恒定,所以通过动力实验获得E0参考值即可计算出G0参考值:
3 工程概况
某水闸位于上海市杭州湾南岸,闸孔组合为15+30+15m,水闸总净宽60m。水闸采取分离式布置方案,两边孔采用倒“Π”型结构形式,中跨一块分离式底板。水闸两侧布置了空箱岸墙结构,引堤填土高度超过13m,水闸坐落在软土地基上,故采取地基处理措施如下:①闸首边孔采用预制方桩基础,桩基长度26m,桩底高程为-29.60m;②空箱岸墙采用三轴搅拌桩复合地基,加固深度25m,底高程为-27.50m;③岸墙两侧15m范围内引堤地基采用三轴搅拌桩加固,加固底高程为-20.00m。闸首地基处理横断面布置图见图3。本工程闸首地基处理方案布局复杂,需统筹考虑上部结构、基础、地基及墙后高填土间的相互作用,常规的经验计算方法已经难以满足设计计算要求,需采用整体有限元计算方法进行模拟分析[1-2]。
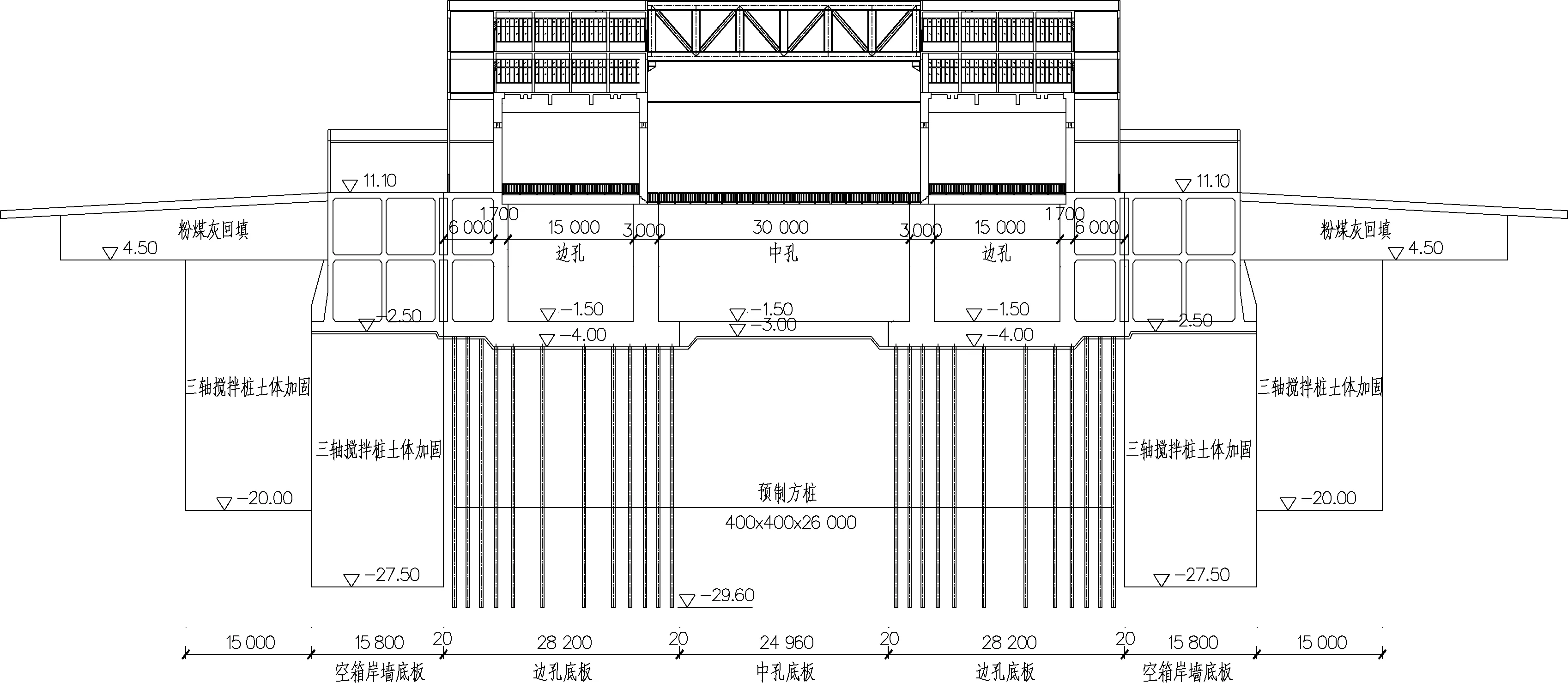
图3 闸首地基处理横断面布置示意
4 有限元模型建立
4.1 模型参数的确定
HS模共有11 个模型参数,分别如下:
3 个Mohr-Coulomb强度参数:c为有效粘聚力;φ为有效内摩擦角;ψ为剪胀角。
HSS模型在HS基础上增加2个小应变特性参数:G0为小应变初始模量;γ0.7为剪切应变。
计算中不同分层土体的重度、粘聚力、摩擦角等参数由勘察报告提供,刚度参数和高级参数则参照王卫东[3-4]等对上海地区土体硬化模型参数研究成果进行确定。
加固区土体压缩模量参照上海市《地基处理技术规范》(DGTJ08-40—2010)第7.2.7条进行确定,计算公式如下:
Eup=mEp+(1-m)Es
式中 Eup为复合地基压缩模量,Ep为搅拌桩压缩模量,Es为桩间土压缩模量,m为置换率。
土层及加固体参数具体见表1。

表1 HSS模型土层参数一览
4.2 有限元模型建立
为充分考虑边载对主体结构的影响,模型水平向考虑范围为200m,模型边缘与闸首中心线距离100m;为充分模拟地基土沉降变形,地基土模拟深度达到-60m。建立模型尺寸为200m(水平)×71m(竖直)。计算模型及网格划分见图4。

图4 计算模型及网格划分示意
5 数值模拟结果
5.1HS模型计算结果
工程竖向位移云图见图5,各部位底板位置值见图6。
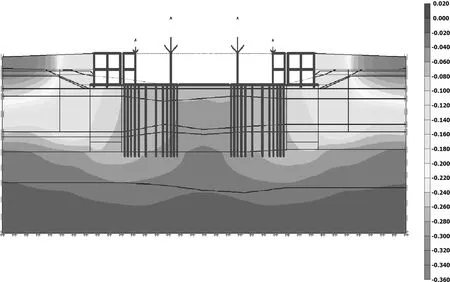
图5 HS模型垂直位移云图(单位:m)

图6 HS模型各底板垂直位移值
5.2HSS模型计算结果
工程竖向位移云图见图7,各部位底板位置值见图8。

图7 HSS模型垂直位移云图(单位:m)

图8 HSS模型各底板垂直位移值
6 对比分析
本工程建设期间对水闸中墩、边墩及岸箱角点进行了全程跟踪监测,监测点布置见图9。本工程于2013年5月通水,截至2014年6月,水闸主体结构的沉降位移已基本趋于平稳,各主要监测点位移与数值模拟沉降变形量对比见图10。

图10 实测监测值与计算值对比(单位:mm)
根据对比可知:
1)HS模型与HSS的计算沉降整体位移区域与实测值均相近,呈现出边板大,中板小的趋势。这主要是由于水闸外河侧翼墙墙后填土高程较内河侧高,受外河侧边载效应较大的影响,引起水闸外河侧出现较大的沉降。故两个模型均基本上反应了本工程软土地基水闸基础沉降形态。
2)HSS模型边板最大沉降值为113.21mm,HS模型边板最大沉降值为124.78mm,相对实测值98~107mm,HSS模型变形值较小,更接近实测数据。
3)HS模型中孔沉降为76.61~77.96mm,大于边孔沉降值。而实测表明,中孔沉降值为39~50mm,小于边孔沉降,故HS模型在中孔的沉降数值及趋势上与实测值差异较大。HSS模型中孔沉降为55.31~50.61mm,小于边孔沉降,趋势与实测数据一致,且沉降数值与实测值更为接近。故HSS模型在中孔变形形态和数值精度上均优于HS模型。
7 结语
1)HSS模型是基于硬化模型理论的基础上考虑了土体剪切刚度与应变的非线性关系,考虑了土体小应变情况下的剪切模量退化性能,进一步丰富了模型土体参数,计算结果更符合实测数值,验证了HSS模型在上海软土地基水闸工程中的适用性。
2) 软土地区水闸工程地基处理需统筹考虑上部结构、基础、地基及墙后高填土间的相互作用,常规的经验计算方法已经难以满足设计计算要求,不能依靠经验,而应采用有限元方法理论,选取合适的土体本构模型,以更好的指导工程优化设计。
3) 从理论计算、施工监测、再到总结分析对比的有机结合,达到理论和实践的相辅相成,合理的制定土体物理力学参数,从而实现技术增长、安全施工与经济效益的多赢成果。
[1] 胡兆球. 水闸结构设计现代计算方法及其应用研究[D].南京:河海大学,2003.
[2] 关淑萍,张燎军,王大胜,等. 边荷载对水闸地基沉降与底板内力的影响研究[J]. 水电能源科学,2006(2):58-60,4.
[3] 尹骥. 小应变硬化土模型在上海地区深基坑工程中的应用[J]. 岩土工程学报,2010(S1):166-172.
[4] 王卫东,王浩然,徐中华. 上海地区基坑开挖数值分析中土体HS-Small模型参数的研究[J]. 岩土力学,2013,34(6):1 766-1 774.
(本文责任编辑 马克俊)
Research on the Design of Sluice Foundationin Soft Soil Area by HSS Model
WU Yi1,YANGYongbao2,TIAN Liyong3
(1.Shanghai rong he City planning and design Co.,LTD Shanghai 200072; 2.Shanghai baoshan district embankment sluice management Shanghai 200439; 3Shanghai Water Engeineering Design and Research Institute Co.LTD Shanghai 200061)
This paper describes the theoretical basis of Hardening Soil Model and Hardening Soil Small-Model in the geotechnical finite element analysis.Discuss the choice of parameters. A Shanghai sluicewhich located in the South Bank of Hangzhou Bay sluice as an example,use HS-Model and HSS-Model calculated by FEA,comparedthe results with the measured data. The calculation results show that the HSS model simulation results and monitoring results of the process of engineering construction is more consistent,which meansthe HSS-Model can better side load, the interaction between the foundation and the upper structure, can optimize the design of the sluice engineering guide complex foundation.
HSS-Model;sluice; soft soil;finite element analysis
2016-03-16;
2016-04-02
吴逸(1984),男,硕士,工程师,从事水利水电工程设计工作。
TU471+.8
A
1008-0112(2016)02-0026-06
